- 1小程序面试题 | 10.精选小程序面试题
- 2MMseg可视化结果分析工具_mmsegmentation可视化log
- 3交通预测论文笔记《Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting》_时空注意力机制
- 4tritonserver学习之一：triton使用流程
- 5CentOS7搭建Hadoop集群(V3.3.4)_centos7安装hadoop集群
- 6自制macOS安装镜像iso虚拟机用_macos iso
- 7[日常] 面试知识点总结(持续更新)
- 8vite 结合vue3.0 打包报错_[plugin:rollup-plugin-dynamic-import-variables] un
- 9Bert微调技巧实验大全_利用bert进行预训练加微调的实例
- 10查漏补缺之（一）—— fasttext与TextCNN_fasttext textcnn
【Roadmap to learn LLM】Large Language Models in Five Formulas
赞
踩
by Alexander Rush
Our hope: reasoning about LLMs
Our Issue
the five formulas
- perpexity —— generation
- attention —— memory
- GEMM —— efficiency
- Chinchilla —— scaling
- RASP —— reasoning
Perpexity(Generation)
simplified language 文档 word tokens 词典
language model 文档的概率模型
p
(
x
1
,
x
2
,
.
.
.
,
x
T
;
θ
)
p(x_1, x_2, ..., x_T; \theta)
p(x1,x2,...,xT;θ)
chain rule 利用chain rule 将joint probability转换为conditional probability
p
(
x
1
,
.
.
.
,
x
T
)
=
∏
t
=
1
T
p
(
x
t
∣
x
1
,
.
.
.
,
x
t
−
1
)
p(x_1, ..., x_T) = \prod_{t=1}^Tp(x_t|x_1, ..., x_{t-1})
p(x1,...,xT)=∏t=1Tp(xt∣x1,...,xt−1)
Auto-Regressive，自动从之前的结果即已有tokens预测之后的token
word classification：每一个条件概率都可以被视为一个采样，在word tokens字典上形成一个概率分布
sampling：条件概率告诉我们每次采样一个word token
Markovian
一些假设
n-grams/Markovian假设：word
x
t
x_t
xt 仅仅依赖于离他一定距离以内的有限个word tokens
categorical假设：下一个单词的概率可以用分类分布来建模
Shannon
这样一个问题：如何度量一个language model的语言建模能力有多强
Metric：Accuracy
words和language遵循zipfian Distribution（长尾效应、幂律关系、最省力原则）
常见的单词占据了概率分布的一大部分，预测不同单词（有着不同的分布频率）情形出现的概率不同，因而不能直接用预测的单词对不对来评判语言模型预测下一个单词的能力，因为零概率单词的存在
处理方法：将概率转换为二进制字符串，字符串的长度是通过概率计算得到的，并且字符串长度 L L L满足 L = − l o g 2 p ( x t ∣ x 1 , . . . , x t − 1 ) L = -log_2p(x_t|x_1,..., x_{t-1}) L=−log2p(xt∣x1,...,xt−1)
p e r p l e x i t y = 2 − ∑ t l o g 2 p ( x t ∣ x 1 , . . . , x t − 1 ) / T perplexity = 2^{-\sum_tlog_2p(x_t|x_1,..., x_{t-1})/T} perplexity=2−∑tlog2p(xt∣x1,...,xt−1)/T
在Wall Street Journal上进行语言建模的perplexity结果
为什么perplexity重要
语言建模可以直接用于其他任务。举个例子，法语到英语的机器翻译可以理解为将法语句子和已经生成的英文words共同作为条件来predict下一个word。
->语言模型的perplexity与将其用于下游任务的效果密切相关
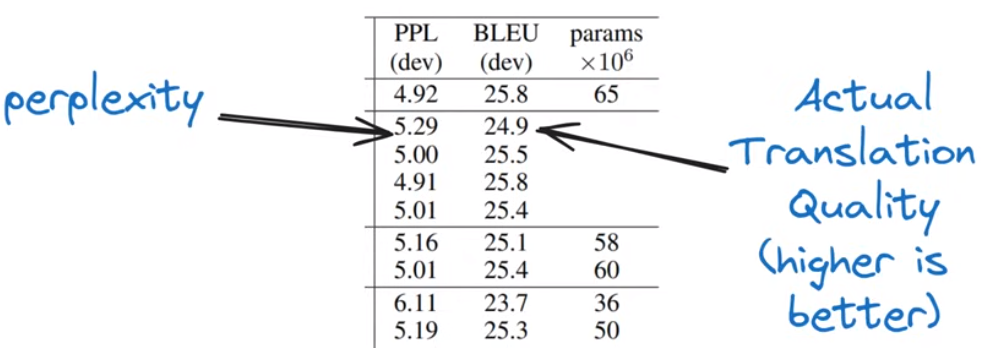
->语言模型的perplexity越低，它的泛化能力越强，甚至是在训练之外的任务上
->现在，perplexity已经作为llm性能的重要衡量指标，我们甚至可以相信说，一个有着更低perplexity的llm会在整体性能上都更好
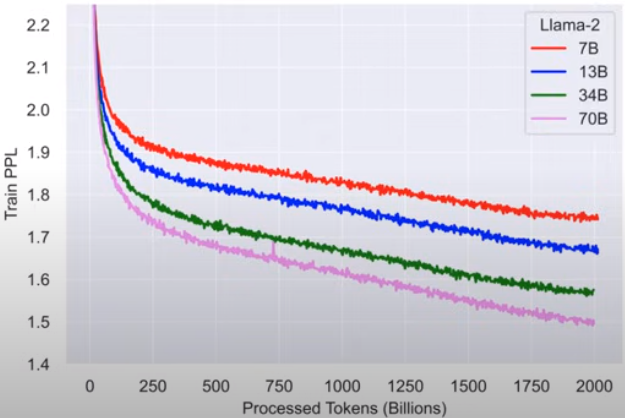
从Shannon的模型到GPT-3
两个主要假设
- 使用深度神经网络模型
- 在预测下一个token时考虑已经生成的全部tokens
Attention(Memory)
语言模型参数化
Markovina假设：
p
(
x
t
∣
x
t
−
2
,
x
t
−
1
;
θ
)
p(x_t|x_{t-2}, x_{t-1};\theta)
p(xt∣xt−2,xt−1;θ) 通过前两个单词预测当前单词
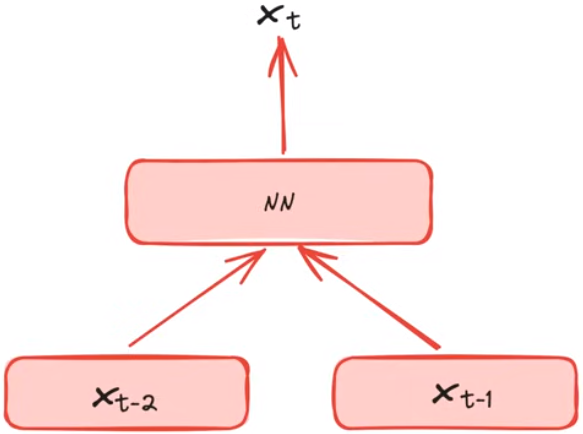
神经网络语言模型
s
o
f
t
m
a
x
(
N
N
(
x
t
−
2
,
x
t
−
1
)
)
softmax(NN(x_{t-2}, x_{t-1}))
softmax(NN(xt−2,xt−1)) 得到下一个单词的预测概率分布
x
t
−
2
x_{t-2}
xt−2和
x
t
−
1
x_{t-1}
xt−1均为one-hot向量，预测的
x
t
x_t
xt也为一个one-hot向量
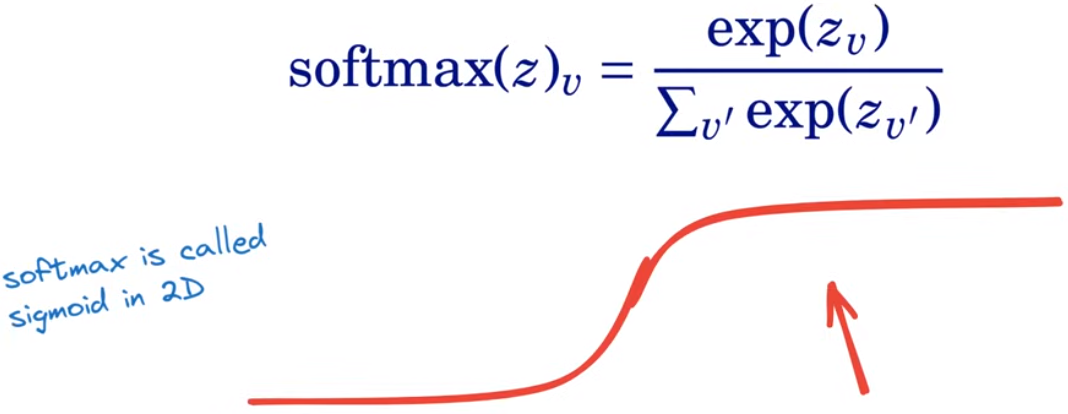
softmax
将输出转化为词汇表上的概率分布，保证词汇表上每个word对应的概率均为正且所有word的概率加和为1
s
o
f
t
m
a
x
(
z
)
v
=
e
x
p
(
z
v
)
∑
v
′
e
x
p
(
z
v
′
)
softmax(z)_v = \frac{exp(z_v)}{\sum_{v'}exp(z_{v'})}
softmax(z)v=∑v′exp(zv′)exp(zv)
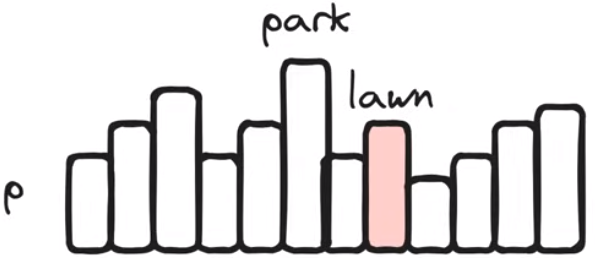
Early Breakthrough: Word2Vec
很重要的一个模型，之后语言建模技术的基础
深度语言模型
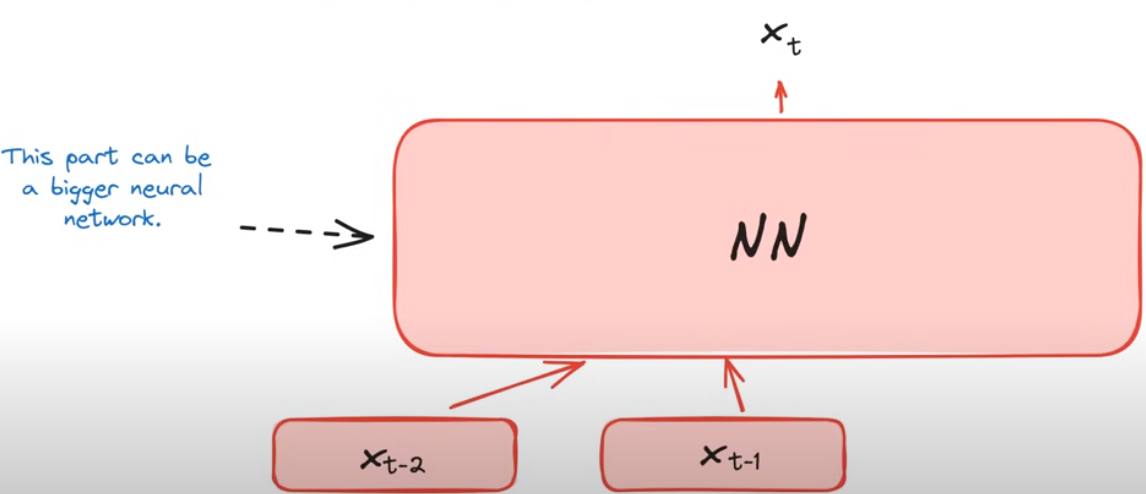
这样的语言建模存在的问题
有些token的预测依赖于长上下文的，而当前的语言模型仅仅只考虑了前两个token，传递的信息是不够的
举个例子：这里需要语言模型输出一个在之前段落中提到过的人的姓氏，这对于一个仅仅考虑tokens nearby的语言模型而言是不可能完成的
Fully Auto-Regressive Models
完全自回归模型，理论上这些模型是使用所有以前的tokens来预测接下来的token
p
(
x
t
∣
x
1
,
.
.
.
,
x
t
−
1
;
θ
)
p(x_t|x_1, ..., x_{t-1}; \theta)
p(xt∣x1,...,xt−1;θ)
为什么是注意力机制而不是普通的神经网络
普通的神经网络不能对上下文进行动态的语言建模，举个例子，当我们在预测position 7的token时，普通的神经网络将学习到关于position 7的非常具体的信息
解决方案：Attention
当今所有llm的核心
类似于随机读取的缓存"RAM"或者跳表
将之前的信息缓存起来为之后的使用做准备
Attention的使用
举个例子，现在我们需要语言模型预测the blank word。在使用注意力机制的时候，我们有一个query vector和一个lookup table，lookup table是之前所有token的相关信息，存储形式为key-value的键值对。当语言模型进行预测任务时，query vector在lookup表里与所有key值进行匹配得到与待预测token最相关的key，将它的value值传递到后面的深度神经网络中，从而完成预测token任务
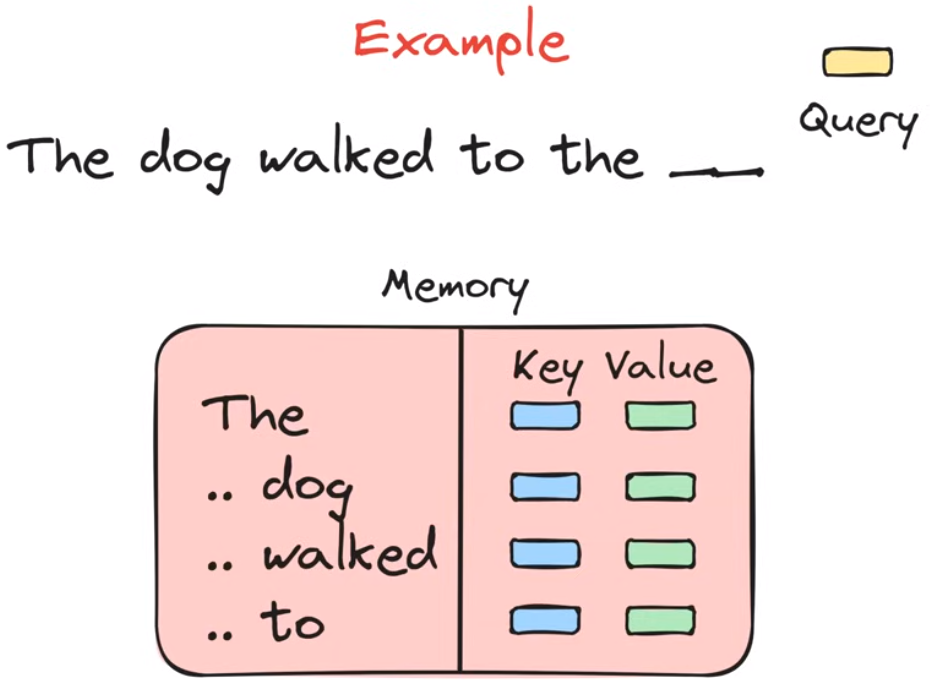
总结一下Attention mechanism做了什么事情
存在的问题
argmax函数不存在导数
解决办法：将argmax函数替换为softmax函数，从而生成先前tokens的位置分布
将argmax改为softmax后的新process
在第二步使用softmax函数求得各个位置key的标准化分数，在第三步对各个位置的分数值进行加权得到最后的结果传递给深度神经网络
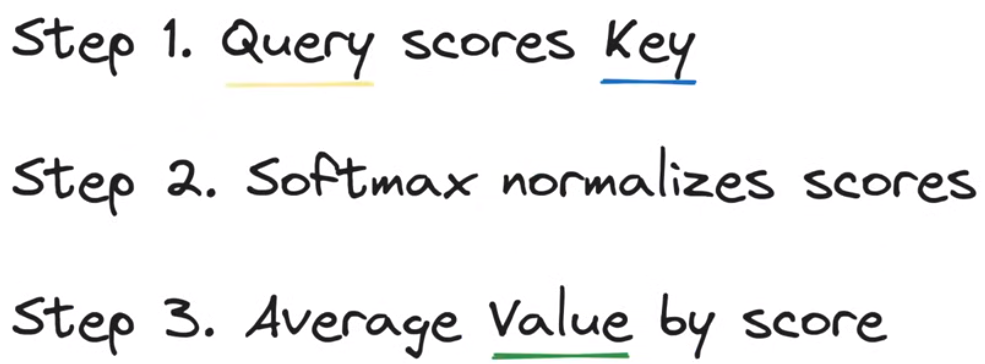
Attention is all you need(2017)
语言建模领域的重要论文，揭示了深度神经网络+注意力=Transformer
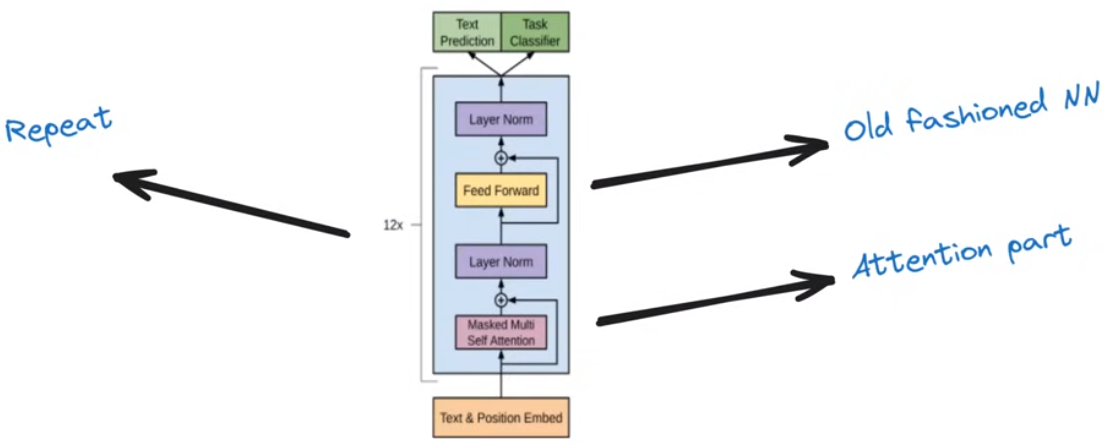
Tranformer结构
由两个阶段构成，第一个阶段是注意力机制，第二个阶段是深度神经网络。这两个阶段在最后的预测之前会重复多次
如何解释llm中的注意力
Attention就像记忆一样
Tranformer架构中使用的Attention机制高效且并行化能力高
Final Process
我们得到了这样一个完整的自回归语言模型，这个模型被称为"generative language model"
这样一个计算过程包括矩阵乘法和softmax计算，是高度可并行化的，利用GPU加速
GEMM(Efficiency)
general purpose GPUs
GPU在llm构建过程中发挥的核心地位，GPU/算力直接决定我们能够构建出什么样性能的llm
用softmax的计算说明GPU发挥的巨大作用
在GPU广泛使用之前，softmax函数的分母计算给CPU造成了巨大的挑战，很多研究都在探究怎么样找到一个近似的函数来对分母的求和进行逼近。而当2010年之后GPU通用编程开始兴起，这个计算变成了一个很简单的问题
用矩阵乘法说明GPU的工作原理
GPU是什么
大量并行运行的PC，有着多个线程，可以同时运行相同的代码
下面将一个GPU线程比作一个小机器人，对GPU的结构进行说明：
GPU线程
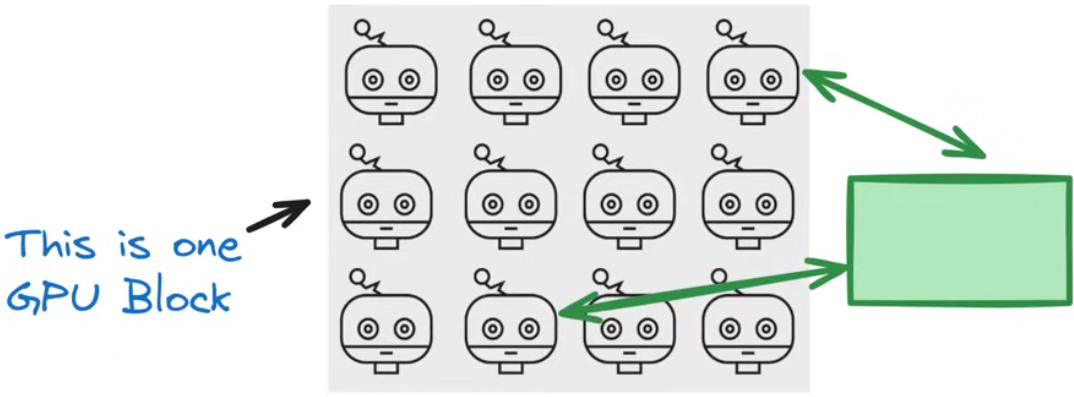
GPU block
一个block中的所有线程（这里是12个）同时运行相同的代码，从block的local memory存取数据是快且高效的
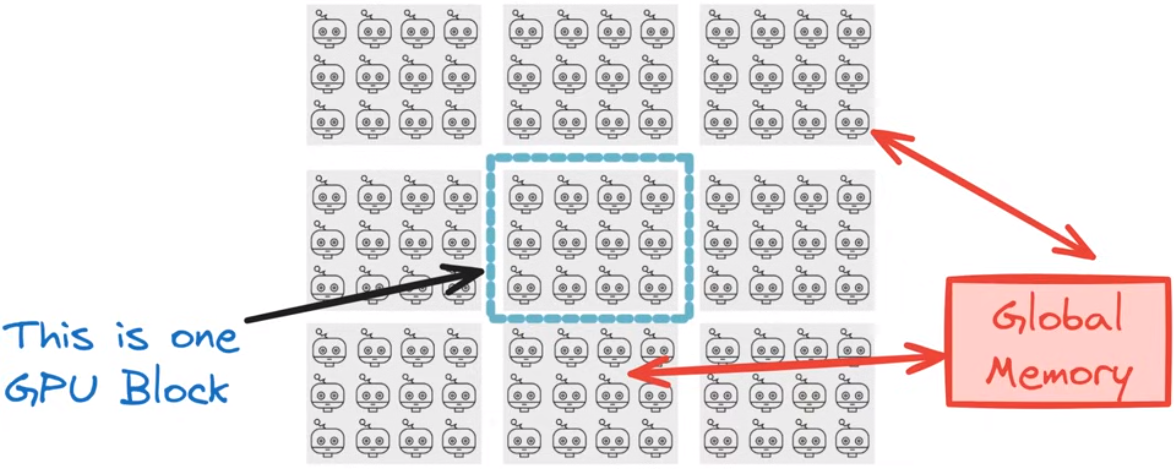
GPU Grid
一个Grid对应了一个全局memory被所有线程共享，线程从这个全局memory中读取数据是更慢的
规则
局部性原理，通过在整个grid中进行block分块，使得块内线程读取块内存储相较于全局存储是更高效的
GPU中的分层存储
全局存储和本地存储直接有交换关系，每个线程只会读取本地线程以获得更高效的性能
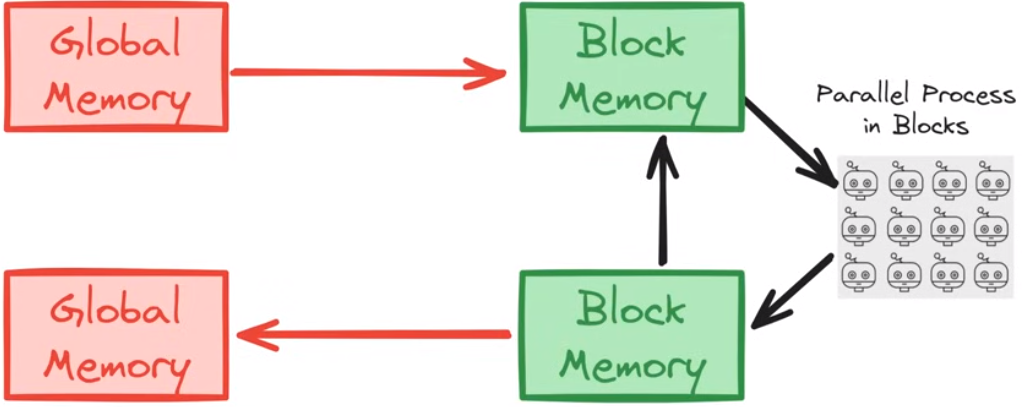
举个例子进行说明
3X3的矩阵乘法在GPU上的运算过程
B
A
BA
BA
如果在计算结果的一个项时只使用一个线程，会带来大量低效的全局访存操作
GPU使用的方法，先将待乘的矩阵数据读取缓存到块存储中，再进行计算
step1: 从全局存储中将待计算的矩阵数据读取到block存储中
step2: 在block存储中计算矩阵乘法
step3: 从block存储中将计算结果写回全局存储
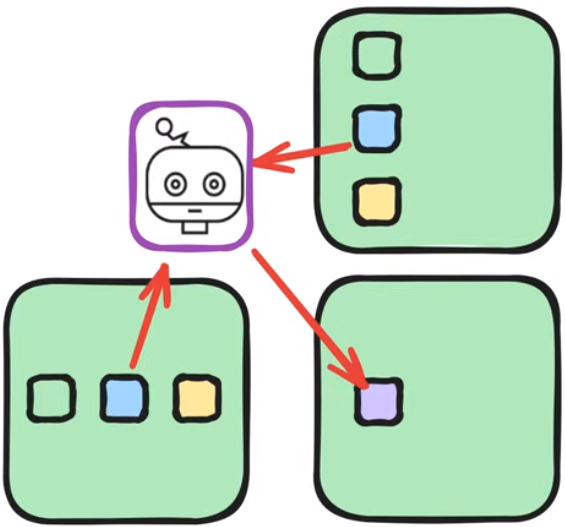
两种方法的对比
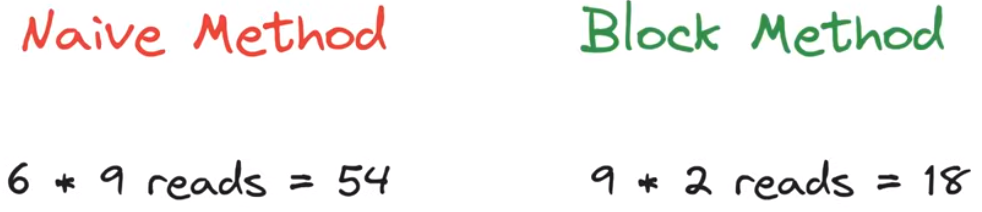
GEMM
更generally的情况是，还会给矩阵乘法结果加上一个矩阵作为偏置项
Chinchilla(Scaling)
预训练阶段的两个变量
llm的参数量和训练数据量
在考虑计算量的时候，数据量和参数量这两个变量形成了乘法关系(a multiplicative relationship)：每个参与训练的token需要与每个参数进行计算
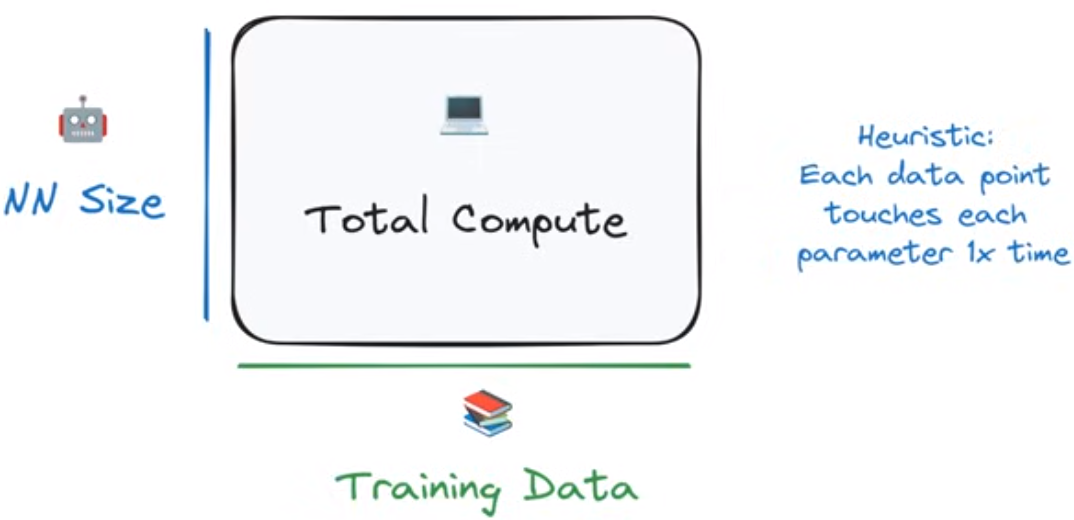
Scaling Laws
大语言模型的性能随着模型规模、训练数据量和使用的计算资源的增大而增强，它们之间满足幂律。log perplexity与计算资源大致成一个线性关系
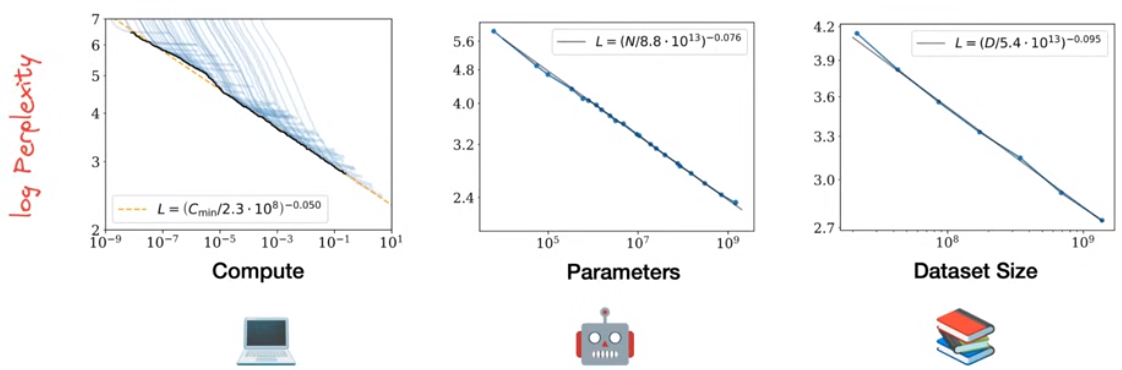
一个直觉性的结论：尽可能地增加模型参数量和训练数据量
存在的问题
计算资源总是有限的，我们应当如何分配，模型参数量和训练数据量之间的分配比例？
如下图所示，我们应该使用更多的训练数据（左图）还是使用更多的模型参数量（右图）
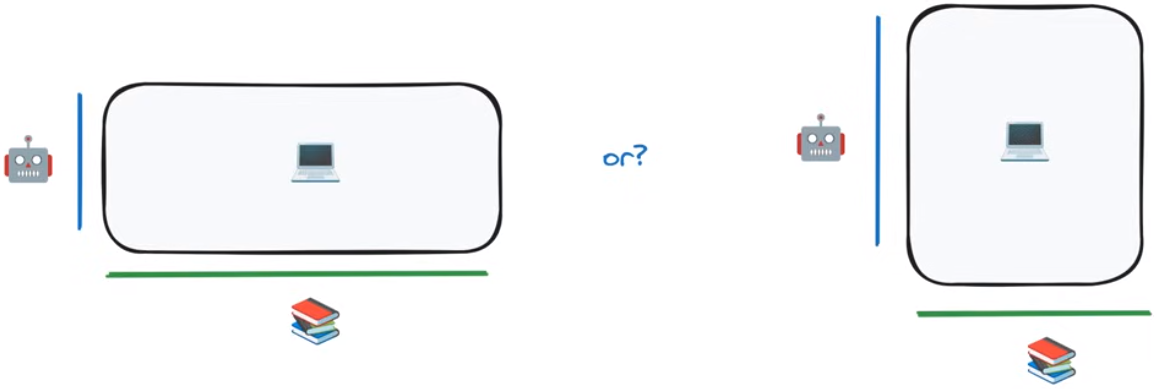
如何找到最佳的计算资源分配
使用模型参数量
N
N
N和训练数据量
D
D
D拟合语言模型的perplexity，拟合结果如下图中的公式所示：
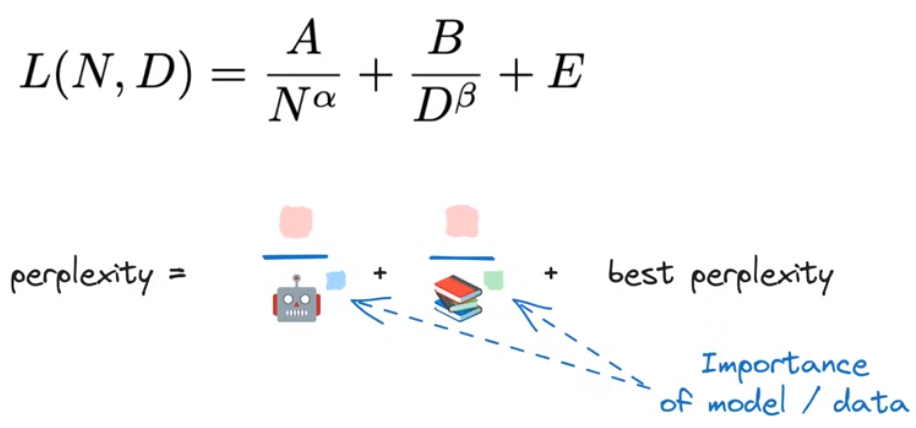
最后的结果——Chinchilla
模型参数量和训练数据量的重要程度大致相当，因而如果我们以大致相等的比例缩放数据和模型，将会得到有限计算资源下最好的perplexity，即最好的llm
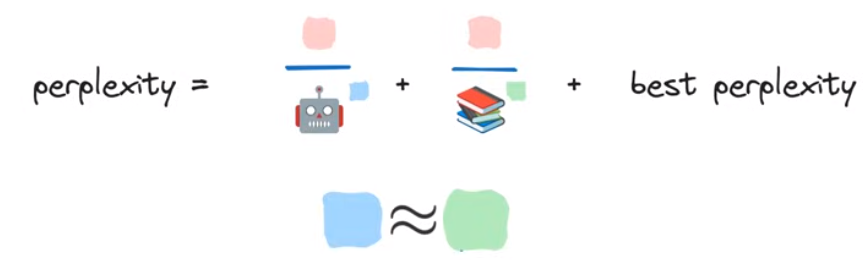
不同模型的参数-训练数据量比展示：
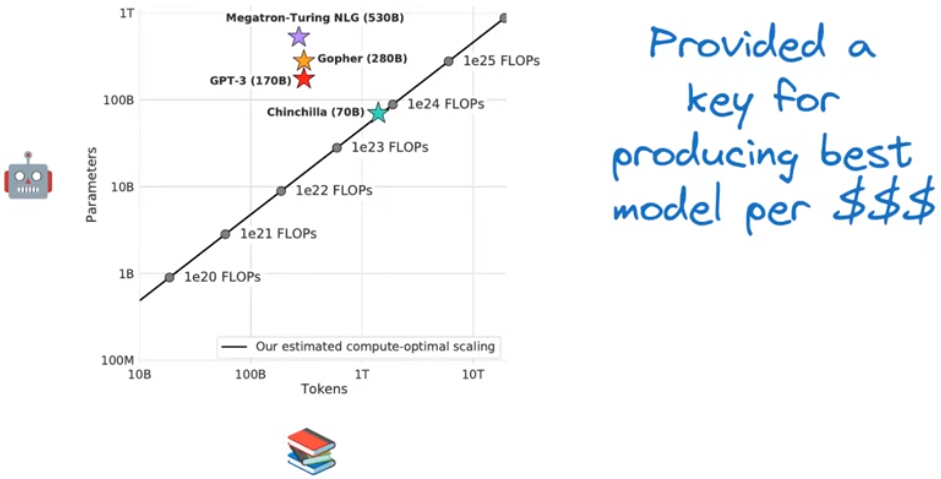
注意：推理运用
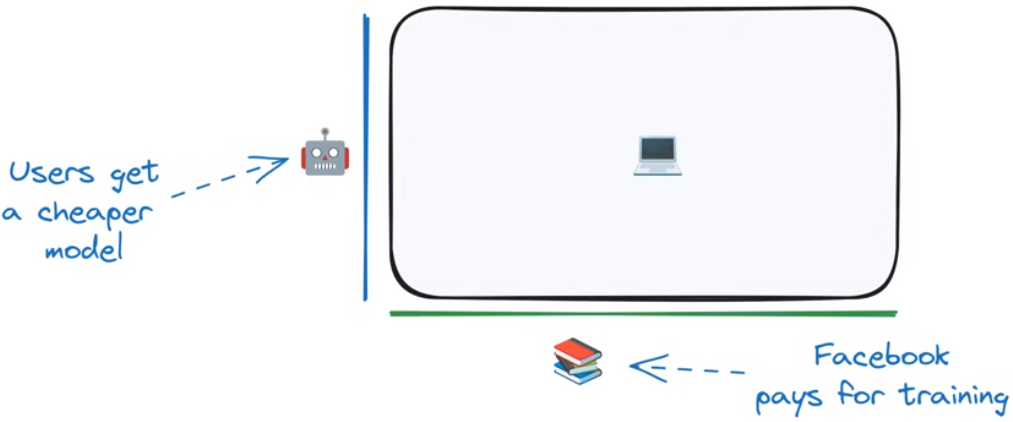
在训练过程中故意使用一个不对称的N/D，比如使用相对更多的训练数据，使用一些计算资源来得到一个相对更小的模型
举个例子：Llama
RASP(Reasoning)
到目前为止，我们所做的，让模型在巨大的训练数据集上进行训练，我们的评测指标只是llm的perplexity是否下降，然后依赖“perplexity的下降会带来llm在其他相关任务上同样有更好的性能”，进行模型的训练优化。
但是我们并不知道也没有办法解释llm到底学到了什么
RASP
一种可以被翻译为一个Transformer语言模型的形式语言，类似于有限自动机
RASP编程
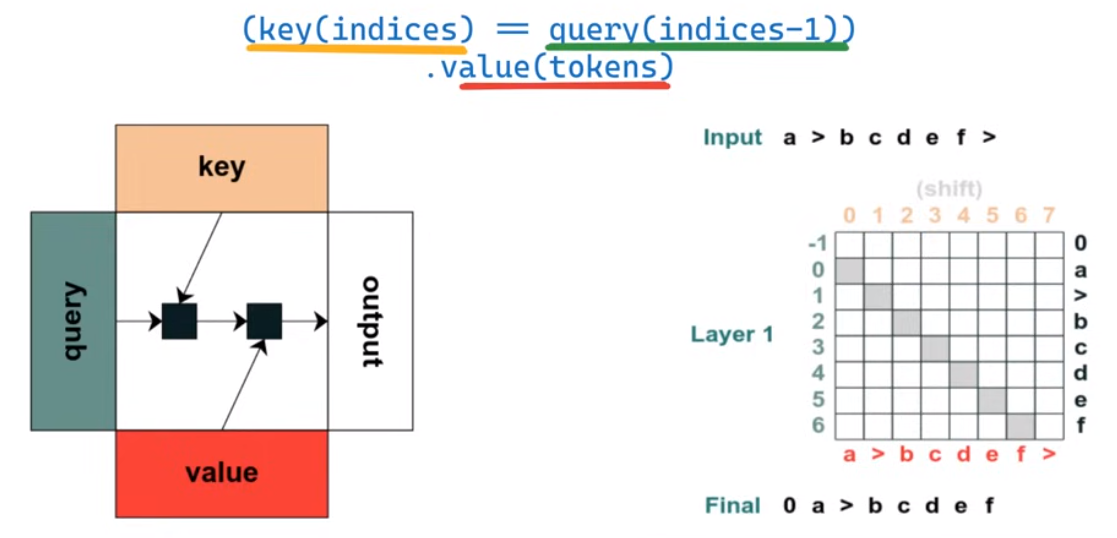
每一个操作都类似于注意力机制中的操作，将query vector、key vector和value vecotr转换为output
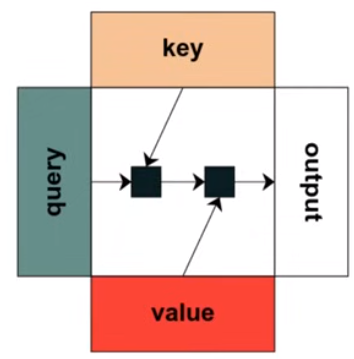
几个RASP程序
没怎么看懂，应该是通过RASP语言实现了Transformer中一个个简单的操作并直观地展示出来
第一个程序，匹配所有索引小于查询索引的key-value
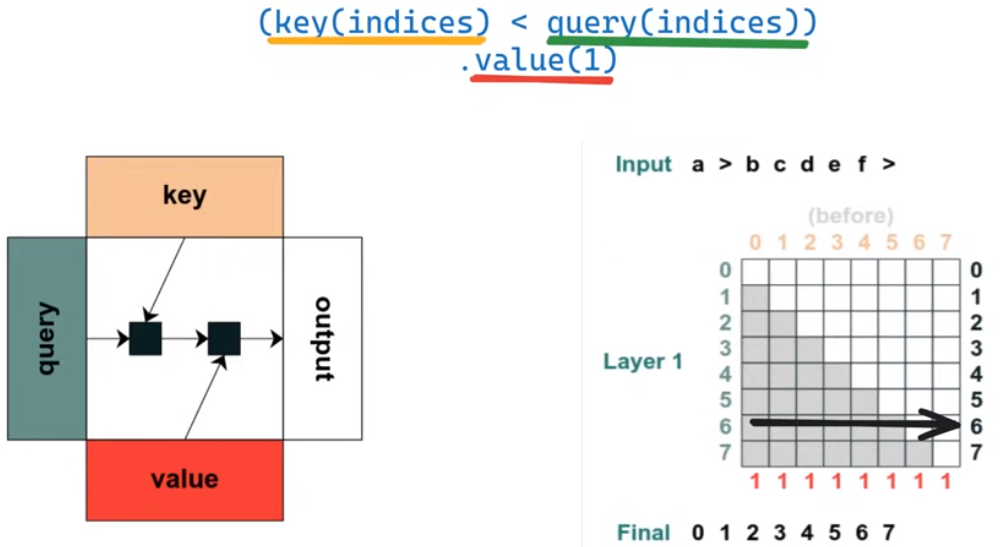
第二个程序，将input序列右移一个位
结论
LLM的五个公式相关的研究都在不断发展
将人类反馈（RLFH）纳入模型优化的评价指标，作为对perplexity的扩展
考虑全部的input序列，是否有除开Transformer之外的其他架构
GPU的新架构、新扩展
Transformer带来硬件如何相互协调工作？以及其他有关llm可解释性的研究
