LeetCode中与单链表有关的题目(C语言)

1.反转链表

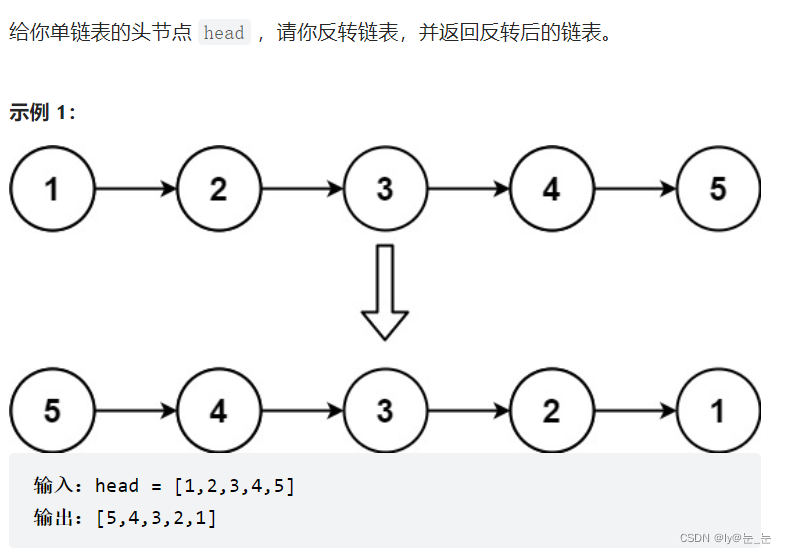
翻转链表，只需知道链表的特性：链表由下一个结点找不到上一个结点，所以必须要记住下一个结点。用两个指针进行翻转，还需用一个指针承接上下。三个指针如下所示：

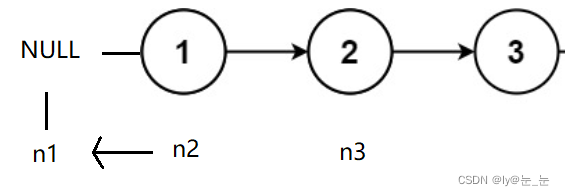
我们用n1,n2翻转，用n3记录下一个结点的位置，结束条件就是当n3为空时，因为当n3为空时，就不能再指向下一个结点，所以最后再将n2->next = n1;

struct ListNode* reverseList(struct ListNode* head)
{
    if (head == NULL || head->next == NULL)
        return head;
    struct ListNode* n1 = NULL, *n2 = head, *n3 = head->next;
    while (n3)
    {
        n2->next = n1;
        n1 = n2;
        n2 = n3;
        n3 = n3->next;
    }
    n2->next = n1;
    return n2;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

或者结束条件当n2为空，不过就要给n3加个条件，如下（效率就变低了）：

struct ListNode* reverseList(struct ListNode* head)
{
    if (head == NULL || head->next == NULL)
        return head;
    struct ListNode* n1 = NULL, *n2 = head, *n3 = head->next;
    while (n2)
    {
        n2->next = n1;
        n1 = n2;
        n2 = n3;
        if (n3 != NULL)
            n3 = n3->next;
    }
    return n1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

2.链表的中间结点

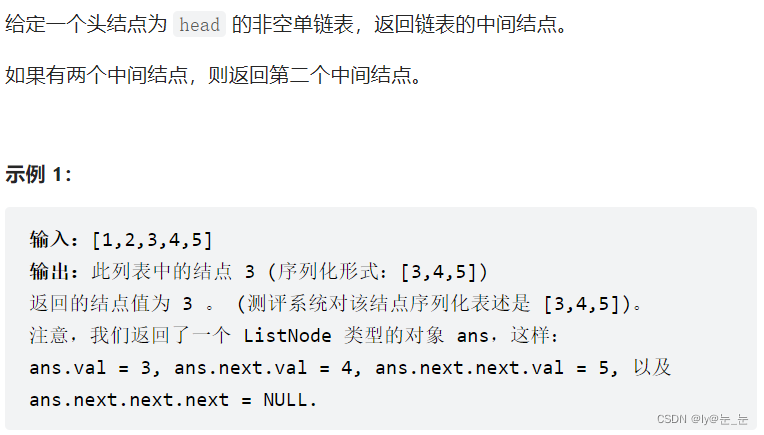
返回链表的中间结点，这里使用快慢指针，慢指针走一步，快指针走两步，当快指针走完链表，慢指针刚好走到链表中间。循环条件：快指针为空或者快指针的下一个结点为空都代表快指针将链表走完。代码如下：

struct ListNode* middleNode(struct ListNode* head)
{
    if (head == NULL || head->next == NULL)
        return head;
    struct ListNode* fast = head, *slow = head;
    while (fast != NULL && fast->next != NULL)
    {
        slow = slow->next;
        fast = fast->next->next;
    }
    return slow;
}
1
2
3
4
5
6
7
8
9
10
11
12

3.链表中倒数第k个结点

可以定义两个指针，让快指针先走k步，然后让快慢指针每次同行一步，直到快指针指向空节点，慢指针就是倒数第k个节点。如果链表为空指针或者k等于0，则返回NULL。代码如下：

struct ListNode* FindKthToTail(struct ListNode* pListHead, int k )
{
    // write code here
    if (pListHead == NULL || k <= 0)
        return NULL;
    struct ListNode* slow = pListHead, *fast = pListHead;
    while (k--)
    {
        if (fast)
            fast = fast->next;
        else
            return NULL;
    }
    while (fast)
    {
        slow = slow->next;
        fast = fast->next;
    }
    return slow;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

4. 合并两个有序链表

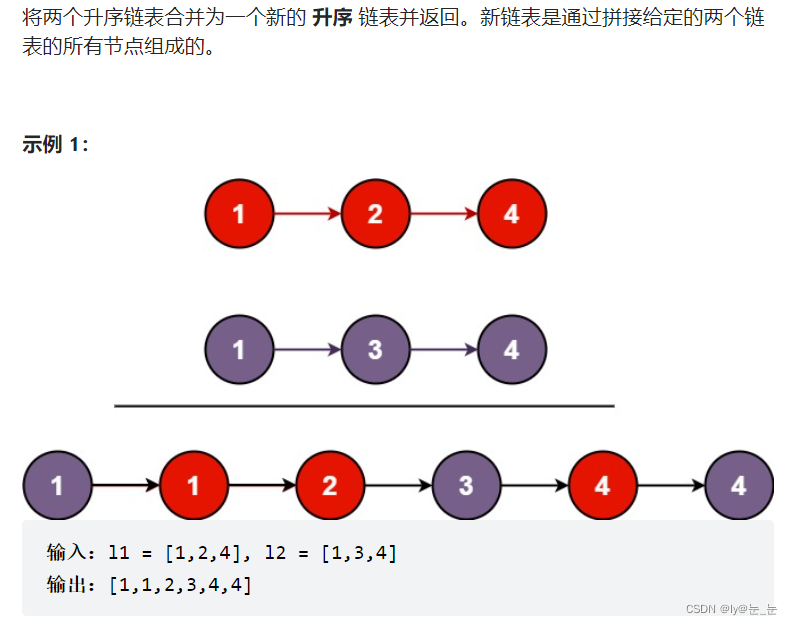
将每个结点逐个对比，进行插入。

struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2)
{
    struct ListNode* head, * cur;
    //先判断是否有空
    if (list1 == NULL && list2 != NULL)
        return list2;
    else if (list1 != NULL && list2 == NULL)
        return list1;
    else if (list1 == NULL && list2 == NULL)
        return NULL;

    //给head附头
    if (list1->val <= list2->val)
    {
        head = cur = list1;
        list1 = list1->next;
    }
    else
    {
        head = cur = list2;
        list2 = list2->next;
    }
    while (list1 || list2)//两个都空结束
    {
        //判断遍历时是否有空
        if (list1 == NULL && list2 != NULL)
        {
            cur->next = list2;
            return head;
        }
        else if (list1 != NULL && list2 == NULL)
        {
            cur->next = list1;
            return head;
        }
        if (list1->val <= list2->val)
        {
            cur->next = list1;
            cur = cur->next;
            list1 = list1->next;
        }
        else
        {
            cur->next = list2;
            cur = cur->next;
            list2 = list2->next;
        }
    }
    cur->next = NULL;
    return head;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

5.相交链表

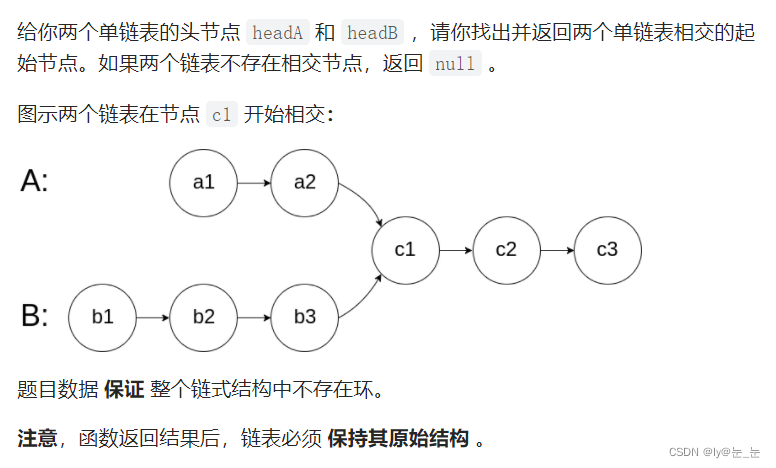
长短链表，计算出差距，然后使步数一样，最后一起向后遍历。

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB)
{
    struct ListNode* cur1 = headA,*cur2 = headB;
    //两条链表的长度
    int length1 = 0,length2 = 0;
    while(cur1->next)
    {
        length1++;
        cur1 = cur1->next;
    }
    while(cur2->next)
    {
        length2++;
        cur2 = cur2->next;
    }
    if(cur1 != cur2)
        return NULL;
    //找出长链表
    struct ListNode* longlist = headA,*shortlist = headB;
    if(length1 < length2)
    {
        longlist = headB;
        shortlist = headA;
    }
    //找差距
    int gap = abs(length1 - length2);
    while(gap--)
    {
        longlist = longlist->next;
    }
    //同时走，找交点
    while(longlist != shortlist)
    {
        longlist = longlist->next;
        shortlist = shortlist->next;
    }
    return longlist;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

6.环形链表 I (判断有环)

快慢指针，即慢指针一次走一步，快指针一次走两步，两个指针从链表其实位置开始运行，
如果链表带环则一定会在环中相遇，否则快指针率先走到链表的末尾。

 bool hasCycle(struct ListNode *head)
{
    struct ListNode* slow = head,*fast = head;
    while(fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        if(slow == fast)
        {
            return true;
        }
    }
    return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

为什么快指针每次走两步，慢指针走一步可以？
假设链表带环，两个指针最后都会进入环，快指针先进环，慢指针后进环。当慢指针刚进环时，可能就和快指针相遇了，最差情况下两个指针之间的距离刚好就是环的长度。此时，两个指针每移动一次，之间的距离就缩小一步，不会出现每次刚好是套圈的情况，因此：在满指针走到一圈之前，快指针肯定是可以追上慢指针的，即相遇。
快指针一次走3步，走4步，…n步行吗？
每次快指针走3步，慢指针走1步，是永远不会相遇的，快指针刚好将慢指针套圈了，因此不行。只有快指针走2步，慢指针走一步才可以，因为换的最小长度是1,即使套圈了两个也在相 同的位置。

7.环形链表 II (返回链表开始进入环的第一个结点)

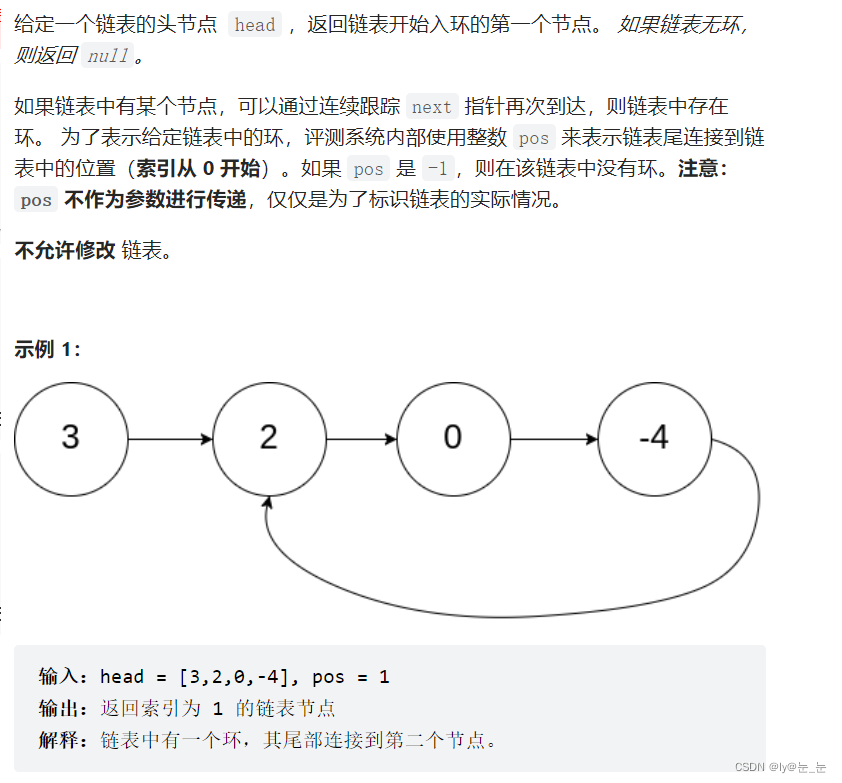
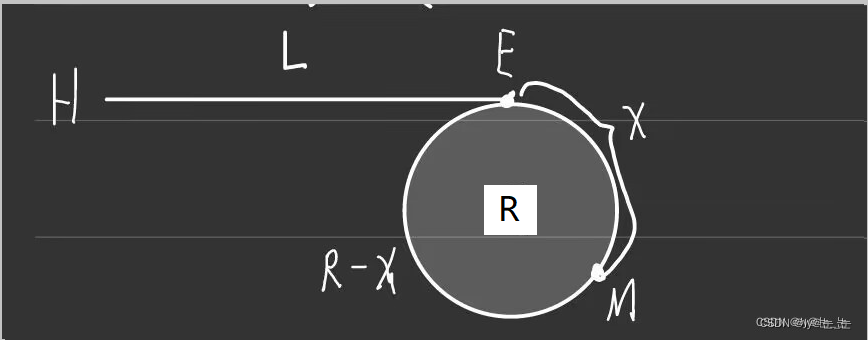
说明： H为链表的起始点，E为环入口点，M与判环时候相遇点
设： 环的长度为R,H到E的距离为L ，E到M的距离为X，则：M到E的距离为R-X， 在判环时，快慢指针相遇时所走的路径长度： fast : L + X + nR， slow:L+X
注意： 1.当慢指针进入环时，快指针可能已经在环中绕了n圈了，n至少为1 因为：快指针先进环走到M的位置，最后又在M的位置与慢指针相遇 2.慢指针进环之后，快指针肯定会在慢指针走一圈之内追上慢指针 因为：慢指针进环后，快慢指针之间的距离最多就是环的长度，而两个指针 在移动时，每次它们至今的距离都缩减一步，因此在慢指针移动一圈之前快 指针肯定是可以追上慢指针的 而快指针速度是满指针的两倍，因此有如下关系是： 2(L+X)=L+X+nR*，L+X=nR， L=nR-X (n为1,2,3,4……，n的大小取决于环的大小，环越小n越大） 极端情况下，假设n=1,此时：L=R-X 即：一个指针从链表起始位置运行，一个指针从相遇点位置绕环，每次都走一 步，两个指针最终会在入口点的位置相遇。

struct ListNode *detectCycle(struct ListNode *head) 
{
    struct ListNode* slow = head,*fast = head;
    while(fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        if(slow == fast)
        {
            struct ListNode* cur = head;
            while(slow != cur)
            {
                slow = slow->next;
                cur = cur->next;
            }
            return slow;
        }
    }
    return NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20