机器学习 正则化l1怎么用_机器学习中的正则化

1 正则化的背景和作用

问题背景：机器学习的参数太多，会导致模型的复杂度上升，容易产生过拟合。

正则化的原理：在损失函数上增加某些限制，减少求出过拟合解的可能性。

作用：

1. 对参数进行约束，降低模型复杂度，从而避免过拟合。假设一个线性回归模型，如果参数很大，只要数据有一点点偏移，那么结果的差距就会很大；如果参数很小，那么数据偏移量较多也不会有太大影响，这样模型对于数据就会有一定的抗扰动能力，
2. 相当于将模型的先验知识增加到损失函数中。

常用的正则化方法：L1，L2，

2 范数的定义

与

3 参数稀疏的好处

3.1 特征选择

稀疏的参数可以在一定程度上实现对参数的选择。一般而言，大部分特征不提供信息，或者对预测帮助很小。稀疏算子的引入可以在一定程度上去掉这些没有帮助的特征，即将它们的权重置0，这样就只关注那些权重非0的特征，从而实现对特征的自动选择。

3.2 可解释性

稀疏性可以使参数更容易被分析和解释。如果最后学习到的参数是稀疏的，那么我们有理由相信，最后剩余的这些参数提供的信息量是巨大的、决定性的，只通过对这些决定性的特征进行组合就可以对结果进行预测，那么对这些参数进行分析就容易多了，进而也更容易解释它们。

4 L1和L2正则化的区别

L1范数更容易产生稀疏模型，而L2范数更容易避免过拟合。

4.1 从优化的角度

考虑一个只有两个参数

4.1.1 L1范数

对于L1范数而言，

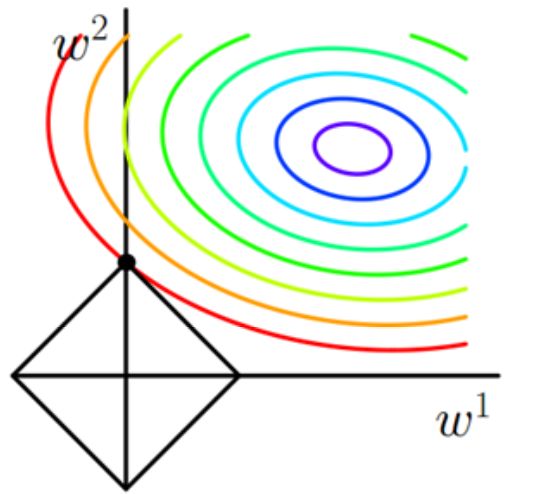
图中横纵坐标分别为

由上图可见，

4.1.2 L2范数

对于L2范数，画出相同的图形如下：

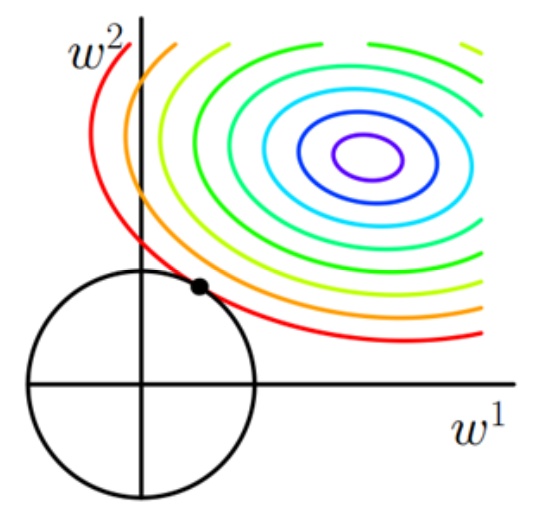
可见L2范数的图形没有“角”，因此

4.2 从梯度的角度

假设存在某线性回归模型，其损失函数为：

由梯度下降得到的权重迭代更新公式为：

其中

4.2.1 带有L1范数的损失函数梯度

带有L1范数的损失函数为：

其梯度为：

参数迭代更新公式为：

其中

4.2.2 带有L2范数的损失函数梯度

带有L2范数的损失函数为：

其梯度为：

参数迭代更新公式为：

4.2.3 两者梯度的区别

在参数更新时，L1范数对应的梯度为

当

此外，当

4.3 从先验的角度

为损失函数加入正则化项，相当于为

L1正则化相当于为