- 1是德科技 DSOX3034A DSOX3054A示波器
- 2Mybatis之关联关系映射_
- 3二分查找:最多需要多少次?二分查找最多要检查多少个元素? Python_二分查找最坏情况下比较次数
- 4ubuntu下安装git安装及使用_ubuntu安装本地git 8081登陆
- 5五分钟,零基础也能入门 Python 图像文字识别_图片识别python
- 6[Unity 3D]如何把几个物体组合在一起_unity怎么把几个物体合成一个
- 7自动驾驶合集13_3dgs数据集 车辆
- 8零基础学会Stable Diffusion!保姆级教程!
- 9路面病害检测-从数据清洗到模型部署的全流程方案_路面病害数据集
- 10最新版的配音软件--- tts-vue 软件 下载安装成功过程
2024年五一数学建模竞赛C题论文首发_2024五一建模论文成品c题
赞
踩
基于随机森林的煤矿深部开采冲击地压危险预测
摘要
煤炭作为中国重要的能源和工业原料,其开采活动对国家经济的稳定与发展起着至关重要的作用。本文将使用题目给出的数据探索更为高效的数据分析方法和更先进的监测设备,以提高预警系统的准确性和可靠性。
对于问题一,干扰信号分析,分析干扰信号并识别干扰信号的时间区间。首先对数据集进行数据清洗,判断其异常值以及缺失值。利用matlab的find函数判定得出无缺失值,再利用k-s检验判定数据分布方式。得出所有的数据均不服从正态分布检验,因此使用箱型图判定异常值。对于判定结果结合实际情况进行分析处理。首先利用给出数据使用固定大小的窗口遍历整个数据集,计算每个窗口中的数据特征。计算幅度差、噪声水平、持续时间、频率特征等。使用提取的特征通过TreeBagger函数训练一个包含100棵决策树的随机森林分类模型。利用问题一特定时间段内的电磁辐射和声发射数据导入模型进行分类判定。随机森林模型的准确率高达99.78%,实现对干扰信号的高精度识别
对于问题二,前兆特征信号分析,分析前兆特征信号并识别前兆特征信号的时间区间。首先,采用与问题一相同的数据清洗方式对问题二涉及的数据进行数据清洗。采用滑动窗口方法计算每个窗口的平均值、标准差和能量等指标。使用随机森林算法训练分类模型,目的是从特征中学习区分类别A和B的模式。利用问题二特定时间段内的电磁辐射和声发射数据导入模型并对其执行与训练数据相同的预处理和特征提取步骤。识别并合并连续或近连续的预测为前兆特征的时间窗口,形成连续的时间区间。
对于问题三,前兆特征信号的实时预警,预测前兆特征信号的概率。应用滑动窗口技术,计算每个窗口的滑动平均值、滑动标准差,以及信号的能量。这些统计量能够捕获信号在每个窗口内的基本特征,为后续的模型训练提供输入特征。筛选类别为A和B的数据作为训练集,使用提取的滑动平均值、滑动标准差和能量作为特征,进行随机森林模型的训练。对每个测试数据文件的最后一个数据点使用训练好的随机森林模型进行预测,评估该时刻前兆特征信号出现的概率。
综合所述,我们通过解决上述问题有助于优化煤矿的安全监控系统,提高对冲击地压等灾害的预防和响应能力。
关键词:随机森林、煤矿深部开采、分类模型、数据清洗

26页 1.2万字(无附录)
无水印照片9页
5.1.2 特征提取
我们利用题目给出的数据进行数据处理后,选取特征进行提取
- 信号的统计特征:如平均值、方差、峰度、偏度等。
- 频率分析:使用傅里叶变换分析信号频率组成,识别与常规采矿作业不同的频率特征。
具体提取结果如下所示

图1:可视化结果
信号波动:信号在不同时间点显示出显著的波动性。有些时间段内,信号振幅显著增加,这可能表明发生了一些异常活动或外部干扰。
峰值:图中存在若干尖锐的峰值,这些峰值可能指示某种突发事件或设备的突然响应。
主要频率成分:频率分布主要集中在较低频段,这表明信号的主要变化是较缓慢的波动。没有明显的高频干扰或尖锐的频率峰值,这通常与机械振动或电子设备的正常运行模式相符。
低频强度:低频成分的强度较高,这可以是由于数据收集过程中的背景噪声或是由传感器本身的性质决定。
平均值(Mean):约77.96,这个值提供了信号平均水平的信息。较高的平均值可能与环境背景或常态运行水平相关。方差(Variance):约8229.37,表明信号在平均水平附近有较大的波动。方差的大小直接反映了信号值分布的散布程度。偏度(Skewness):约3.12,指示信号分布的不对称性和尾部的延伸。正偏度(大于0)意味着信号的尾部向较大值方向延伸。峰度(Kurtosis):约13.00,这是一个高峰度值,表明信号有厚重的尾部并且峰比正态分布更尖锐,这可能指出信号中存在极端值或突出的峰。
5.1.3 干扰信号识别
- 特征提取
1. 振幅(Amplitude)
振幅是描述信号强度的一个基本特征。在处理时序数据,如EMR信号时,通常会考虑信号在一定时间窗口内的最大值和最小值之差作为振幅。这个差值可以帮助我们理解在该时间窗口内信号的变化范围,从而捕捉到可能的异常或显著的变化事件。
2. 噪声水平(Noise Level)
噪声水平通常通过计算信号的标准差来估计,标准差能够反映信号的离散程度。在实际应用中,信号的标准差越大,表明信号在该时间窗内的波动越大,噪声水平也相对较高。
3. 能量(Energy)
能量特征通常用于描述信号在特定时间窗口内的总能量,可以通过计算信号平方的总和来估计。信号的能量越高,表明该时间段内信号的活动更加剧烈或更有可能包含某些事件。
4. 频率分析(Frequency Analysis)
频率分析是通过对信号进行傅里叶变换来完成的,目的是分析信号在频域上的分布。这种分析可以帮助识别信号中的周期性成分或者异常频率的出现。
5.信号波动(Signal Fluctuation)
信号波动可以通过多种方法来量化,一种常见的方法是计算信号在窗口内部的最大变化率,即窗口内相邻点之间差值的最大值。这个度量能够捕捉信号短时间内的剧烈变化,常用于识别突发事件。
6.峰值(Peak Value)
峰值是信号在窗口期间达到的最大值,它提供了信号强度的一个直观指标。在某些情况下,异常高的峰值可能指示设备故障、外部干扰或其他重要事件。
表1:部分数据特征
| 统计特征 | 时间特征 |
| 电磁辐射 (EMR) 统计特征: | 测量时间间隔统计特征: |
| 平均值:77.96 | 平均间隔:约5709秒(约95分钟) |
| 标准差:90.72 | 标准差:约119216秒(因大部分间隔为31秒或62秒,故标准差大表明存在极端值) |
| 最小值:0 | 最小间隔:0秒(连续测量) |
| 第一四分位数:31.62 | 第一四分位数:31秒 |
| 中位数:45.00 | 中位数:31秒 |
| 第三四分位数:75.00 | 第三四分位数:62秒 |
| 最大值:500 | 最大间隔:约5815425秒(约67天) |
特征提取是确保数据科学和机器学习模型有效性的基础。在本案例中,通过振幅、噪声水平、能量和频率分析,我们能够构建出能够有效反映信号特性的特征集,这些特征对于训练分类模型来说是至关重要的。通过这些特征,模型能够学习如何区分正常信号与前兆特征信号,从而在实际应用中提供预警,减少潜在的风险。
- 模型训练
随机森林是一种强大的机器学习算法,属于集成学习方法的一种。它主要用于分类和回归任务,通过结合多个决策树的预测结果来提高整体的预测准确性和鲁棒性。下面详细介绍随机森林的工作原理:
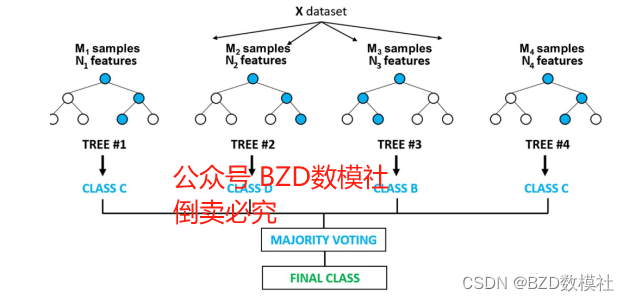
图1:随机森林原理图
表1 电磁辐射干扰信号时间区间
| 序号 | 时间区间起点 | 时间区间终点 |
| 1 | 2022-05-01 10:48:40 | 2022-05-01 11:16:07 |
| 2 | 2022-05-10 06:22:28 | 2022-05-10 06:46:15 |
| 3 | 2022-05-18 06:27:52 | |
| 4 | 2022-05-25 10:30:13 | |
| 5 | 2022-05-28 01:53:22 |
表2 声发射干扰信号时间区间
| 序号 | 时间区间起点 | 时间区间终点 |
| 1 | 11-Oct-2022 10:21:33 | 11-Oct-2022 10: |
| 2 | 16-Oct-2022 02:16:27 | |
| 3 | 16-Oct-2022 09:38:04 | |
| 4 | 17-Oct-2022 00:42:24 | |
| 5 | 22-Oct-2022 23:29:15 | 23-Oct-2022 00:04:16 |
表2 声发射干扰信号时间区间
| 序号 | 时间区间起点 | 时间区间终点 |
| 1 | 03-Apr-2022 09:13:07 | 03-Apr-2022 09:35:10 |
| 2 | 04-Apr-2022 01:07:58 | |
| 3 | 06-Apr-2022 13:27:21 | |
| 4 | 07-Apr-2022 03:17:36 | |
| 5 | 07-Apr-2022 08:28:30 | 07-Apr-2022 10:20:10 |
问题一+数据预处理代码免费分享
百度网盘 请输入提取码
提取码:sxjm
% 导入数据
opts = detectImportOptions('附件一.xlsx');
opts.DataRange = 'A2'; % 假设数据从A2开始
data = readtable('附件一.xlsx', opts);
% 选择要分析的数据列,这里假设是'EMR'
emrData = data.EMR;
% 绘制Q-Q图
figure;
qqplot(emrData);
title('Q-Q Plot of EMR Data');
% 执行K-S检验,检查数据是否符合正态分布
[h, p, ksstat, cv] = kstest((emrData-mean(emrData))/std(emrData)); % 数据标准化
% 显示K-S检验结果
fprintf('K-S Test Result:\n');
fprintf('Hypothesis Rejected (1 = true, 0 = false): %d\n', h);
fprintf('P-value: %g\n', p);
fprintf('KS Statistic: %g\n', ksstat);
fprintf('Critical Value for 5%% Significance: %g\n', cv);
% 导入数据
opts = detectImportOptions('附件一.xlsx');
opts.DataRange = 'A2'; % 假设数据从A2开始
data = readtable('附件一.xlsx', opts);
% 选择要分析的数据列,这里假设是'EMR'
emrData = data.EMR;
% 绘制Q-Q图,并美化结果
figure;
qqplot(emrData);
title('Q-Q Plot of EMR Data', 'FontSize', 14);
xlabel('Theoretical Quantiles', 'FontSize', 12);
ylabel('Sample Quantiles', 'FontSize', 12);
grid on; % 添加网格
set(gca, 'FontSize', 10); % 设置坐标轴字体大小
set(gca, 'Color', [0.95 0.95 0.95]); % 设置坐标轴背景颜色
% 执行K-S检验,检查数据是否符合正态分布
[h, p, ksstat, cv] = kstest((emrData-mean(emrData))/std(emrData)); % 数据标准化
% 显示K-S检验结果
fprintf('K-S Test Result:\n');
fprintf('Hypothesis Rejected (1 = true, 0 = false): %d\n', h);
fprintf('P-value: %g\n', p);
fprintf('KS Statistic: %g\n', ksstat);
fprintf('Critical Value for 5%% Significance: %g\n', cv);
% 导入数据
opts = detectImportOptions('附件一.xlsx');
data = readtable('附件一.xlsx', opts);
% 选择类别C的数据
c_data = data(strcmp(data.class, 'C'), :);
% 计算时间间隔和采样频率
timeIntervals = seconds(diff(c_data.time));
Fs = 1 / mean(timeIntervals); % 假设时间间隔均匀
L = height(c_data);
% 傅里叶变换
Y = fft(c_data.EMR);
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
f = Fs*(0:(L/2))/L;
% 计算振幅、持续时间、噪声水平
amplitudes = max(c_data.EMR) - min(c_data.EMR);
duration = seconds(max(c_data.time) - min(c_data.time));
noise_levels = std(c_data.EMR);
% 统计分析
stats = [mean(c_data.EMR), var(c_data.EMR), skewness(c_data.EMR), kurtosis(c_data.EMR)];
% 数据可视化
figure;
subplot(3,1,1);
plot(c_data.time, c_data.EMR, 'LineWidth', 1.5);
title('EMR Signal Waveform');
xlabel('Time');
ylabel('EMR');
grid on;
subplot(3,1,2);
plot(f, P1, 'b', 'LineWidth', 1.5);
title('Single-Sided Amplitude Spectrum of EMR');
xlabel('Frequency (f) [Hz]');
ylabel('|P1(f)|');
grid on;
subplot(3,1,3);
bar(stats, 'FaceColor', [0 0.5 0.7], 'EdgeColor', [0 0.2 0.3], 'LineWidth', 1.5);
set(gca, 'xticklabel', {'Mean', 'Variance', 'Skewness', 'Kurtosis'});
title('Statistical Metrics of EMR Signal');
grid on;
% 显示统计结果
fprintf('Mean: %.2f\n', stats(1));
fprintf('Variance: %.2f\n', stats(2));
fprintf('Skewness: %.2f\n', stats(3));
fprintf('Kurtosis: %.2f\n', stats(4));
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import kstest, norm
# 加载数据
data_path = '附件一.xlsx'
data = pd.read_excel(data_path)
# 函数用于检查每个类别的数据是否服从正态分布
def check_normal_distribution(group_data):
statistic, p_value = kstest(group_data, 'norm', args=(group_data.mean(), group_data.std()))
return statistic, p_value, p_value > 0.05 # p值大于0.05,接受原假设,认为数据服从正态分布
# 函数用于计算并可视化异常值
def detect_and_visualize_outliers(data, category):
Q1 = data.quantile(0.25)
Q3 = data.quantile(0.75)
IQR = Q3 - Q1
outliers = ((data < (Q1 - 1.5 * IQR)) | (data > (Q3 + 1.5 * IQR)))
# 可视化
plt.figure(figsize=(10, 6))
plt.title(f"Boxplot and Outliers for Category {category}")
plt.boxplot(data, vert=False)
plt.scatter(data[outliers], np.full(data[outliers].shape, 1), color='red', zorder=5)
plt.grid(True)
plt.show()
return outliers
# 按类别分组并检查每组数据分布
distribution_tests = {}
for category, group in data.groupby('类别 (class)'):
emr_values = group['电磁辐射 (EMR)'].dropna() # 删除可能的NaN值
statistic, p_value, is_normal = check_normal_distribution(emr_values)
distribution_tests[category] = {'K-S Statistic': statistic, 'P-Value': p_value, 'Is Normal': is_normal}
# 将检测结果转换为DataFrame进行更好的展示
distribution_tests_df = pd.DataFrame(distribution_tests).T
print(distribution_tests_df)
# 应用异常值检测并进行可视化
outliers_results = {}
for category, group in data.groupby('类别 (class)'):
emr_values = group['电磁辐射 (EMR)'].dropna()
outliers = detect_and_visualize_outliers(emr_values, category)
outliers_results[category] = outliers.sum() # 记录每个类别中异常值的数量
# 输出每个类别的异常值数量
outliers_summary = pd.DataFrame.from_dict(outliers_results, orient='index', columns=['Number of Outliers'])
print(outliers_summary)
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import classification_report
# 加载数据
attachment1_path = '附件一.xlsx'
attachment1_data = pd.read_excel(attachment1_path)
problem1_emr_path = '问题一EMR检测时间.xlsx'
problem1_emr_data = pd.read_excel(problem1_emr_path)
# 数据预处理
X = attachment1_data[['电磁辐射 (EMR)']]
y = attachment1_data['类别 (class)'].apply(lambda x: 1 if x == 'C' else 0) # 'C'为干扰信号
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 标准化特征
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# 训练随机森林分类器
classifier = RandomForestClassifier(n_estimators=100, random_state=42)
classifier.fit(X_train_scaled, y_train)
# 预测并检查模型性能
y_pred = classifier.predict(X_test_scaled)
print(classification_report(y_test, y_pred))
# 应用模型于新数据
problem1_emr_features = scaler.transform(problem1_emr_data[['电磁辐射 (EMR)']])
problem1_emr_data['干扰预测'] = classifier.predict(problem1_emr_features)
# 寻找干扰信号的连续区间
problem1_emr_data['时间 (time)'] = pd.to_datetime(problem1_emr_data['时间 (time)'])
problem1_emr_data.sort_values('时间 (time)', inplace=True)
# 合并95分钟内的干扰信号区间
def merge_intervals(intervals):
sorted_intervals = sorted(intervals, key=lambda x: x[0])
merged = []
current_start, current_end = sorted_intervals[0]
for start, end in sorted_intervals[1:]:
if start - current_end <= pd.Timedelta(minutes=95):
current_end = max(current_end, end)
else:
merged.append((current_start, current_end))
current_start, current_end = start, end
merged.append((current_start, current_end))
return merged
# 提取干扰区间
problem1_emr_data['区间起点'] = (problem1_emr_data['干扰预测'] == 1) & (problem1_emr_data['干扰预测'].shift(1) != 1)
problem1_emr_data['区间终点'] = (problem1_emr_data['干扰预测'] == 1) & (problem1_emr_data['干扰预测'].shift(-1) != 1)
intervals = problem1_emr_data[(problem1_emr_data['区间起点'] | problem1_emr_data['区间终点']) & (problem1_emr_data['干扰预测'] == 1)]
intervals = intervals[['时间 (time)', '区间起点', '区间终点']]
interval_list = [(row['时间 (time)'], row['时间 (time)']) for index, row in intervals.iterrows()]
# 合并区间并可视化
merged_intervals = merge_intervals(interval_list)
fig, ax = plt.subplots(figsize=(10, 2))
y = 1
for start, end in merged_intervals[:5]: # 展示前五个区间
ax.plot([start, end], [y, y], marker='o', color='red')
y += 1
plt.yticks([])
plt.title("Top 5 EMR Interference Intervals")
plt.xlabel("Time")
plt.tight_layout()
plt.show()
# 显示合并后的前五个干扰区间的起点和终点
merged_intervals[:5]



