- 1Microsoft Visual C++ 14.0 is required解决方法_microsoft visual c++ 14.0离线安装
- 2自学大语言模型的应用程序框架Langchain(初入门)_langchain应用框架
- 3vue自定义抽屉组件_vue 抽屉组件 适用手机端
- 4一文学会Axios的使用
- 5STM32F4存储器映射 和 寄存器映射_stm32f4重映射
- 6您知道用 Docker打包 Springboot有多少种方式?
- 7kail-添加静态路由_kali添加路由命令
- 8linux磁盘空间查看及空间满的处理,linux磁盘空间占满问题快速定位并解决
- 9C语言:对称二叉树_对称二叉树c语言
- 10AI之DL:人工智能领域—深度学习的发展历程之深度学习爆发的三大因素、探究DL为什么耗算力
吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(2-1)-- 深度学习的实践方面_cousera deeplearing笔记
赞
踩
作者: 大树先生
博客: http://blog.csdn.net/koala_tree
知乎:https://www.zhihu.com/people/dashuxiansheng
GitHub:https://github.com/KoalaTree
2017 年 09 月 28 日
以下为在Coursera上吴恩达老师的DeepLearning.ai课程项目中,第二部分《改善深层神经网络:超参数调试、正则化以及优化》第一周课程“深度学习的实践方面”关键点的笔记。因为这节课每一节的知识点都很重要,所以本次笔记几乎涵盖了全部小视频课程的记录。同时在阅读以下笔记的同时,强烈建议学习吴恩达老师的视频课程,视频请至 Coursera 或者 网易云课堂。
同时我在知乎上开设了关于机器学习深度学习的专栏收录下面的笔记,方便在移动端的学习。欢迎关注我的知乎:大树先生。一起学习一起进步呀!_
改善深层神经网络:超参数调试、正则化以及优化 —深度学习的实践方面
1. 训练、验证、测试集
对于一个需要解决的问题的样本数据,在建立模型的过程中,我们会将问题的data划分为以下几个部分:
-
训练集(train set):用训练集对算法或模型进行训练过程;
-
验证集(development set):利用验证集或者又称为简单交叉验证集(hold-out cross validation set)进行交叉验证,选择出最好的模型;
-
测试集(test set):最后利用测试集对模型进行测试,获取模型运行的无偏估计。
小数据时代
在小数据量的时代,如:100、1000、10000的数据量大小,可以将data做以下划分:
- 无验证集的情况:70% / 30%;
- 有验证集的情况:60% / 20% / 20%;
通常在小数据量时代,以上比例的划分是非常合理的。
大数据时代
但是在如今的大数据时代,对于一个问题,我们拥有的data的数量可能是百万级别的,所以验证集和测试集所占的比重会趋向于变得更小。
验证集的目的是为了验证不同的算法哪种更加有效,所以验证集只要足够大能够验证大约2-10种算法哪种更好就足够了,不需要使用20%的数据作为验证集。如百万数据中抽取1万的数据作为验证集就可以了。
测试集的主要目的是评估模型的效果,如在单个分类器中,往往在百万级别的数据中,我们选择其中1000条数据足以评估单个模型的效果。
- 100万数据量:98% / 1% / 1%;
- 超百万数据量:99.5% / 0.25% / 0.25%(或者99.5% / 0.4% / 0.1%)
Notation
- 建议验证集要和训练集来自于同一个分布,可以使得机器学习算法变得更快;
- 如果不需要用无偏估计来评估模型的性能,则可以不需要测试集。
2. 偏差、方差
对于下图中两个类别分类边界的分割:
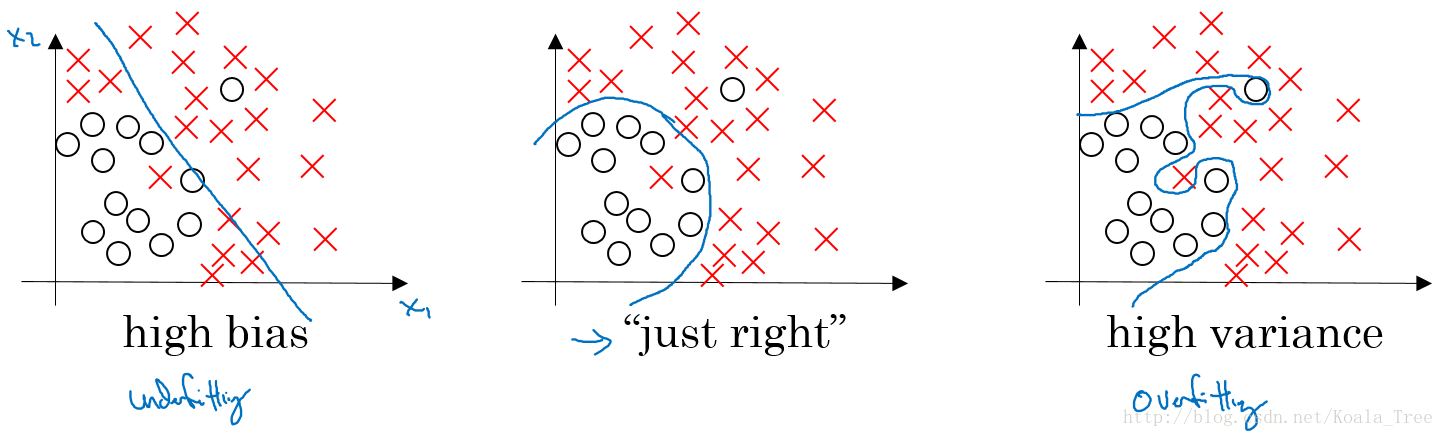
从图中我们可以看出,在欠拟合(underfitting)的情况下,出现高偏差(high bias)的情况;在过拟合(overfitting)的情况下,出现高方差(high variance)的情况。
在bias-variance tradeoff 的角度来讲,我们利用训练集对模型进行训练就是为了使得模型在train集上使 bias 最小化,避免出现underfitting的情况;
但是如果模型设置的太复杂,虽然在train集上 bias 的值非常小,模型甚至可以将所有的数据点正确分类,但是当将训练好的模型应用在dev 集上的时候,却出现了较高的错误率。这是因为模型设置的太复杂则没有排除一些train集数据中的噪声,使得模型出现overfitting的情况,在dev 集上出现高 variance 的现象。
所以对于bias和variance的权衡问题,对于模型来说是一个十分重要的问题。
例子:
几种不同的情况:

以上为在人眼判别误差在0%的情况下,该最优误差通常也称为“贝叶斯误差”,如果“贝叶斯误差”大约为15%,那么图中第二种情况就是一种比较好的情况。
High bias and high variance的情况
上图中第三种bias和variance的情况出现的可能如下:
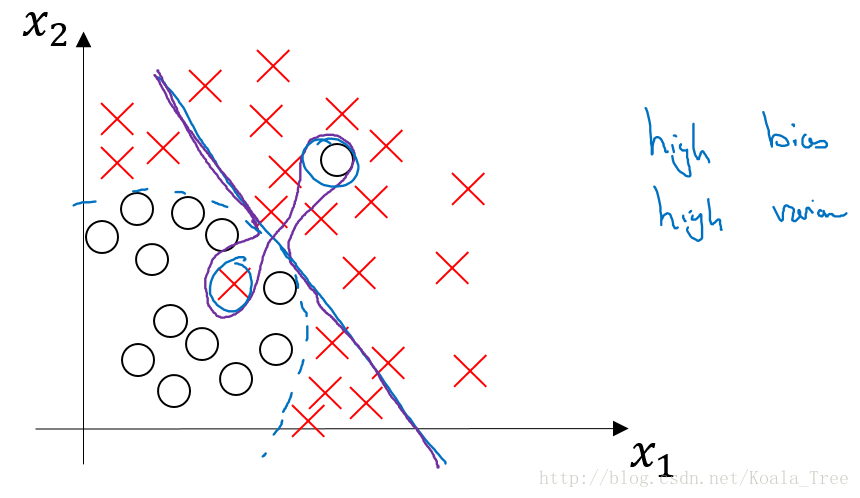
没有找到边界线,但却在部分数据点上出现了过拟合,则会导致这种高偏差和高方差的情况。
虽然在这里二维的情况下可能看起来较为奇怪,出现的可能性比较低;但是在高维的情况下,出现这种情况就成为可能。
3. 机器学习的基本方法
在训练机器学习模型的过程中,解决High bias 和High variance 的过程:
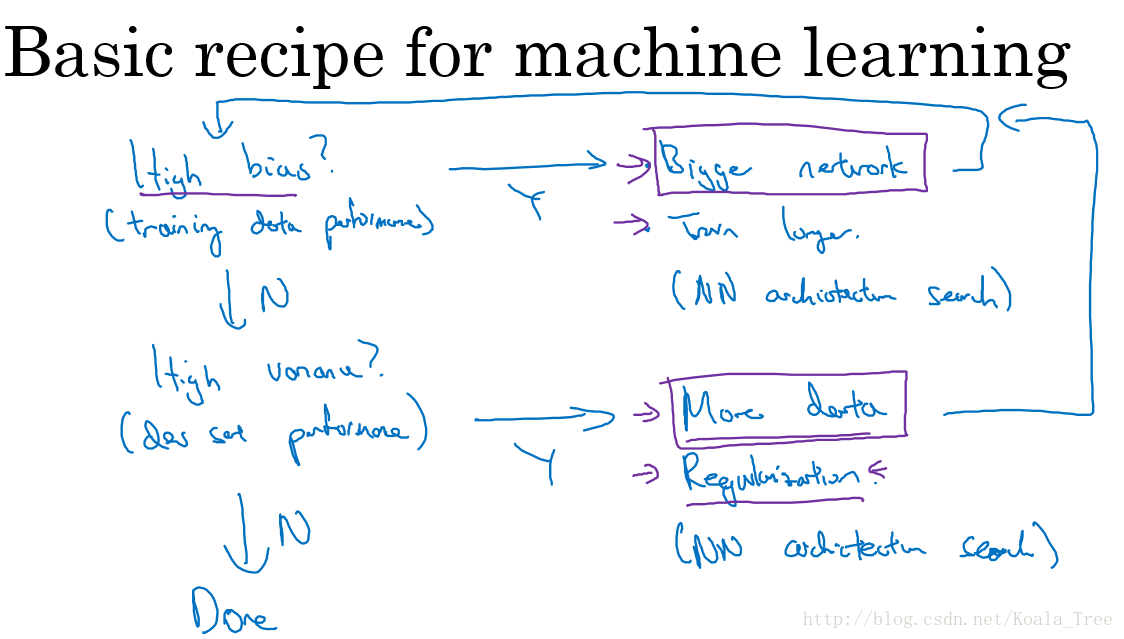
- 1.是否存在High bias ?
- 增加网络结构,如增加隐藏层数目;
- 训练更长时间;
- 寻找合适的网络架构,使用更大的NN结构;
- 2.是否存在High variance?
- 获取更多的数据;
- 正则化( regularization);
- 寻找合适的网络结构;
在大数据时代,深度学习对监督式学习大有裨益,使得我们不用像以前一样太过关注如何平衡偏差和方差的权衡问题,通过以上方法可以使得再不增加另一方的情况下减少一方的值。
4. 正则化(regularization)
利用正则化来解决High variance 的问题,正则化是在 Cost function 中加入一项正则化项,惩罚模型的复杂度。
Logistic regression
加入正则化项的代价函数:
J
(
w
,
b
)
=
1
m
∑
i
=
1
m
l
(
y
^
(
i
)
,
y
(
i
)
)
+
λ
2
m
∣
∣
w
∣
∣
2
2
J(w,b)=\dfrac{1}{m}\sum\limits_{i=1}^{m}l(\hat y^{(i)},y^{(i)})+\dfrac{\lambda}{2m}||w||_{2}^{2}
J(w,b)=m1i=1∑ml(y^(i),y(i))+2mλ∣∣w∣∣22
上式为逻辑回归的L2正则化。
- L2正则化: λ 2 m ∣ ∣ w ∣ ∣ 2 2 = λ 2 m ∑ j = 1 n x w j 2 = λ 2 m w T w \dfrac{\lambda}{2m}||w||_{2}^{2} = \dfrac{\lambda}{2m}\sum\limits_{j=1}^{n_{x}} w_{j}^{2}=\dfrac{\lambda}{2m}w^{T}w 2mλ∣∣w∣∣22=2mλj=1∑nxwj2=2mλwTw
- L1正则化: λ 2 m ∣ ∣ w ∣ ∣ 1 = λ 2 m ∑ j = 1 n x ∣ w j ∣ \dfrac{\lambda}{2m}||w||_{1}=\dfrac{\lambda}{2m}\sum\limits_{j=1}^{n_{x}}|w_{j}| 2mλ∣∣w∣∣1=2mλj=1∑nx∣wj∣
其中 λ \lambda λ为正则化因子。
注意:lambda在python中属于保留字,所以在编程的时候,用“lambd”代表这里的正则化因子
λ
\lambda
λ。
Neural network
加入正则化项的代价函数:
J
(
w
[
1
]
,
b
[
1
]
,
⋯
,
w
[
L
]
,
b
[
L
]
)
=
1
m
∑
i
=
1
m
l
(
y
^
(
i
)
,
y
(
i
)
)
+
λ
2
m
∑
l
=
1
L
∣
∣
w
[
l
]
∣
∣
F
2
J(w^{[1]},b^{[1]},\cdots,w^{[L]},b^{[L]})=\dfrac{1}{m}\sum\limits_{i=1}^{m}l(\hat y^{(i)},y^{(i)})+\dfrac{\lambda}{2m}\sum\limits_{l=1}^{L}||w^{[l]}||_{F}^{2}
J(w[1],b[1],⋯,w[L],b[L])=m1i=1∑ml(y^(i),y(i))+2mλl=1∑L∣∣w[l]∣∣F2
其中 ∣ ∣ w [ l ] ∣ ∣ F 2 = ∑ i = 1 n [ l − 1 ] ∑ j = 1 n [ l ] ( w i j [ l ] ) 2 ||w^{[l]}||_{F}^{2}=\sum\limits_{i=1}^{n^{[l-1]}}\sum\limits_{j=1}^{n^{[l]}}(w_{ij}^{[l]})^{2} ∣∣w[l]∣∣F2=i=1∑n[l−1]j=1∑n[l](wij[l])2,因为 w w w的大小为 ( n [ l − 1 ] , n [ l ] ) (n^{[l-1]},n^{[l]}) (n[l−1],n[l]),该矩阵范数被称为“Frobenius norm”
Weight decay
在加入正则化项后,梯度变为:
d W [ l ] = ( f o r m _ b a c k p r o p ) + λ m W [ l ] dW^{[l]} = (form\_backprop)+\dfrac{\lambda}{m}W^{[l]} dW[l]=(form_backprop)+mλW[l]
则梯度更新公式变为:
W [ l ] : = W [ l ] − α d W [ l ] W^{[l]}:= W^{[l]}-\alpha dW^{[l]} W[l]:=W[l]−αdW[l]
代入可得:
W
[
l
]
:
=
W
[
l
]
−
α
[
(
f
o
r
m
_
b
a
c
k
p
r
o
p
)
+
λ
m
W
[
l
]
]
=
W
[
l
]
−
α
λ
m
W
[
l
]
−
α
(
f
o
r
m
_
b
a
c
k
p
r
o
p
)
=
(
1
−
α
λ
m
)
W
[
l
]
−
α
(
f
o
r
m
_
b
a
c
k
p
r
o
p
)
W^{[l]}:= W^{[l]}-\alpha [ (form\_backprop)+\dfrac{\lambda}{m}W^{[l]}]\\ = W^{[l]}-\alpha\dfrac{\lambda}{m}W^{[l]} -\alpha(form\_backprop)\\=(1-\dfrac{\alpha\lambda}{m})W^{[l]}-\alpha(form\_backprop)
W[l]:=W[l]−α[(form_backprop)+mλW[l]]=W[l]−αmλW[l]−α(form_backprop)=(1−mαλ)W[l]−α(form_backprop)
其中,
(
1
−
α
λ
m
)
(1-\dfrac{\alpha\lambda}{m})
(1−mαλ)为一个
<
1
<1
<1的项,会给原来的
W
[
l
]
W^{[l]}
W[l]一个衰减的参数,所以L2范数正则化也被称为“权重衰减(Weight decay)”。
5. 为什么正则化可以减小过拟合
假设下图的神经网络结构属于过拟合状态:
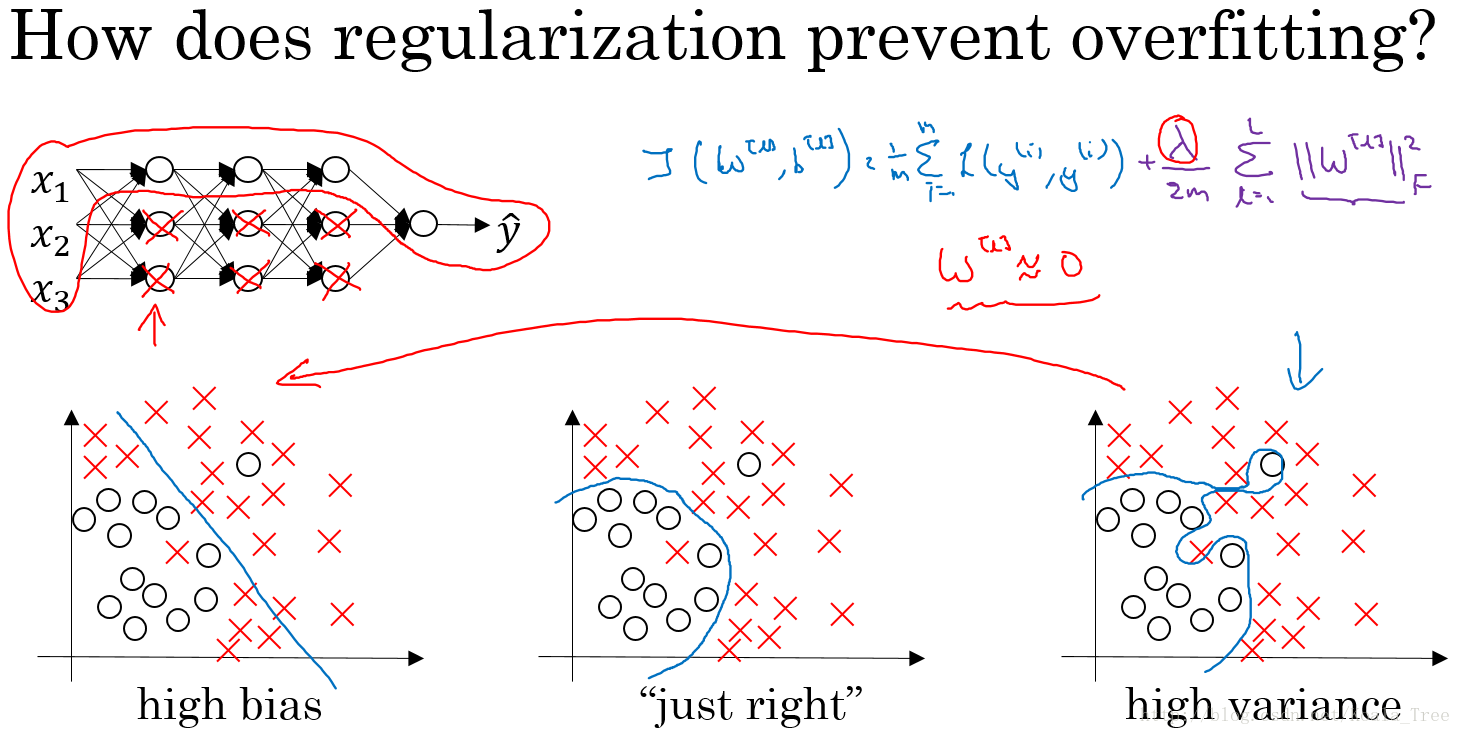
对于神经网络的Cost function:
J
(
w
[
1
]
,
b
[
1
]
,
⋯
,
w
[
L
]
,
b
[
L
]
)
=
1
m
∑
i
=
1
m
l
(
y
^
(
i
)
,
y
(
i
)
)
+
λ
2
m
∑
l
=
1
L
∣
∣
w
[
l
]
∣
∣
F
2
J(w^{[1]},b^{[1]},\cdots,w^{[L]},b^{[L]})=\dfrac{1}{m}\sum\limits_{i=1}^{m}l(\hat y^{(i)},y^{(i)})+\dfrac{\lambda}{2m}\sum\limits_{l=1}^{L}||w^{[l]}||_{F}^{2}
J(w[1],b[1],⋯,w[L],b[L])=m1i=1∑ml(y^(i),y(i))+2mλl=1∑L∣∣w[l]∣∣F2
加入正则化项,直观上理解,正则化因子 λ \lambda λ设置的足够大的情况下,为了使代价函数最小化,权重矩阵 W W W就会被设置为接近于0的值。则相当于消除了很多神经元的影响,那么图中的大的神经网络就会变成一个较小的网络。
当然上面这种解释是一种直观上的理解,但是实际上隐藏层的神经元依然存在,但是他们的影响变小了,便不会导致过拟合。
数学解释:
假设神经元中使用的激活函数为 g ( z ) = tanh ( z ) g(z)=\tanh(z) g(z)=tanh(z),在加入正则化项后:
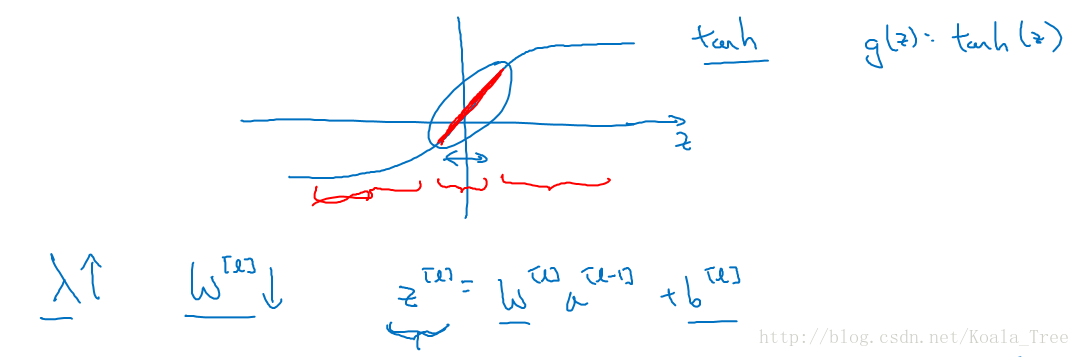
当 λ \lambda λ增大,导致 W [ l ] W^{[l]} W[l]减小, Z [ l ] = W [ l ] a [ l − 1 ] + b [ l ] Z^{[l]}=W^{[l]}a^{[l-1]}+b^{[l]} Z[l]=W[l]a[l−1]+b[l]便会减小,由上图可知,在 z z z较小的区域里, tanh ( z ) \tanh(z) tanh(z)函数近似线性,所以每层的函数就近似线性函数,整个网络就成为一个简单的近似线性的网络,从而不会发生过拟合。
6. Dropout 正则化
Dropout(随机失活)就是在神经网络的Dropout层,为每个神经元结点设置一个随机消除的概率,对于保留下来的神经元,我们得到一个节点较少,规模较小的网络进行训练。
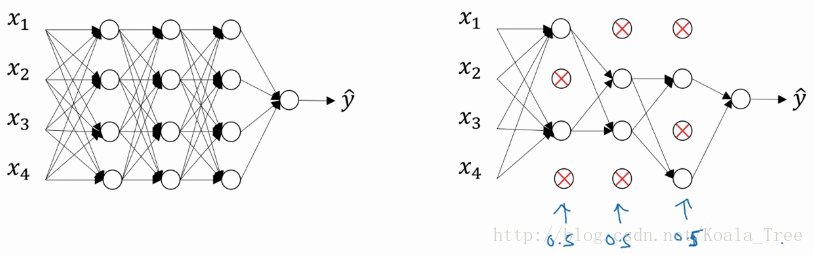
实现Dropout的方法:反向随机失活(Inverted dropout)
首先假设对 layer 3 进行dropout:
keep_prob = 0.8 # 设置神经元保留概率
d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep_prob
a3 = np.multiply(a3, d3)
a3 /= keep_prob
- 1
- 2
- 3
- 4
这里解释下为什么要有最后一步:a3 /= keep_prob
依照例子中的keep_prob = 0.8 ,那么就有大约20%的神经元被删除了,也就是说 a [ 3 ] a^{[3]} a[3]中有20%的元素被归零了,在下一层的计算中有 Z [ 4 ] = W [ 4 ] ⋅ a [ 3 ] + b [ 4 ] Z^{[4]}=W^{[4]}\cdot a^{[3]}+b^{[4]} Z[4]=W[4]⋅a[3]+b[4],所以为了不影响 Z [ 4 ] Z^{[4]} Z[4]的期望值,所以需要 W [ 4 ] ⋅ a [ 3 ] W^{[4]}\cdot a^{[3]} W[4]⋅a[3]的部分除以一个keep_prob。
Inverted dropout通过对“a3 /= keep_prob”,则保证无论keep_prob设置为多少,都不会对 Z [ 4 ] Z^{[4]} Z[4]的期望值产生影响。
Notation:在测试阶段不要用dropout,因为那样会使得预测结果变得随机。
7. 理解 Dropout
另外一种对于Dropout的理解。
这里我们以单个神经元入手,单个神经元的工作就是接收输入,并产生一些有意义的输出,但是加入了Dropout以后,输入的特征都是有可能会被随机清除的,所以该神经元不会再特别依赖于任何一个输入特征,也就是说不会给任何一个输入设置太大的权重。
所以通过传播过程,dropout将产生和L2范数相同的收缩权重的效果。
对于不同的层,设置的keep_prob也不同,一般来说神经元较少的层,会设keep_prob
=1.0,神经元多的层,则会将keep_prob设置的较小。
缺点:
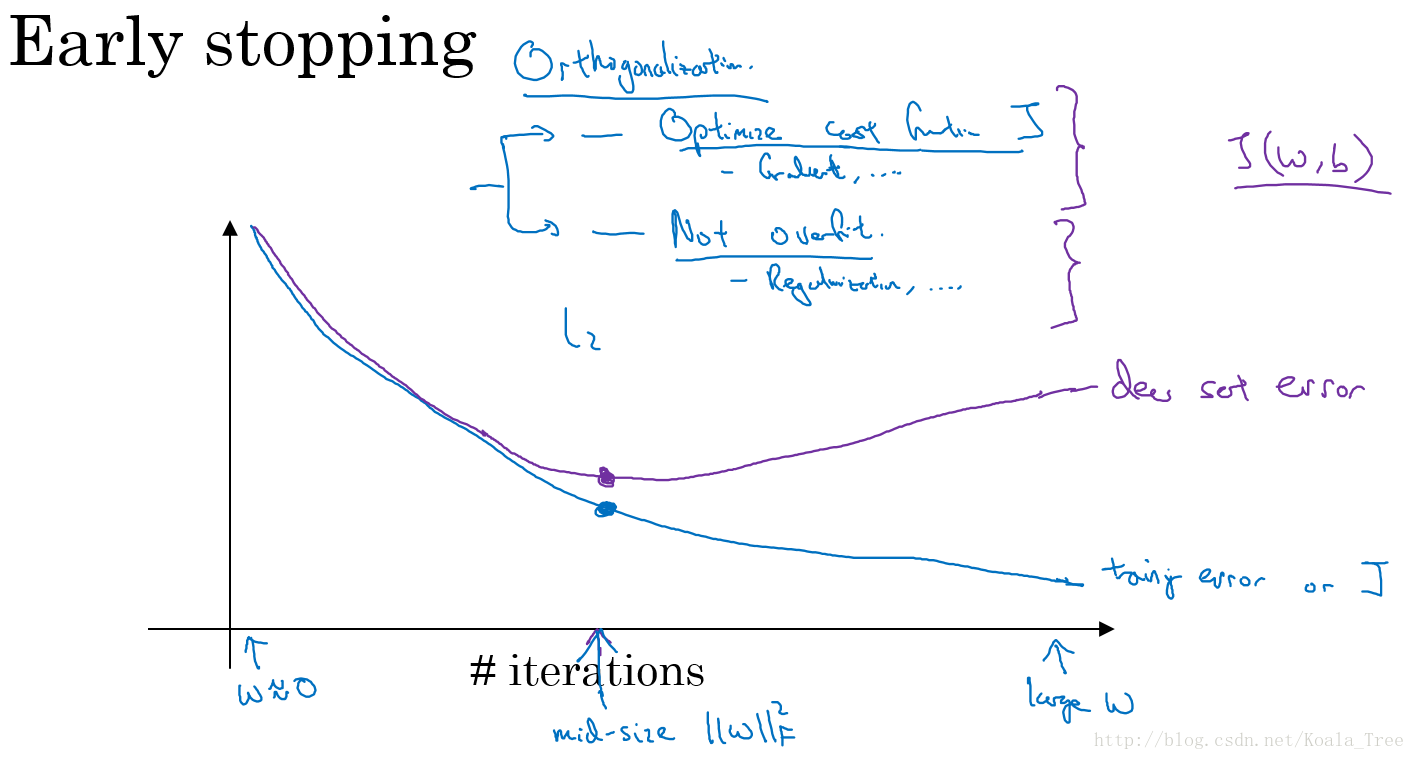
dropout的一大缺点就是其使得 Cost function不能再被明确的定义,以为每次迭代都会随机消除一些神经元结点,所以我们无法绘制出每次迭代 J ( W , b ) J(W,b) J(W,b)下降的图,如下:

使用Dropout:
- 关闭dropout功能,即设置 keep_prob = 1.0;
- 运行代码,确保 J ( W , b ) J(W,b) J(W,b)函数单调递减;
- 再打开dropout函数。
8. 其他正则化方法
- 数据扩增(Data augmentation):通过图片的一些变换,得到更多的训练集和验证集;
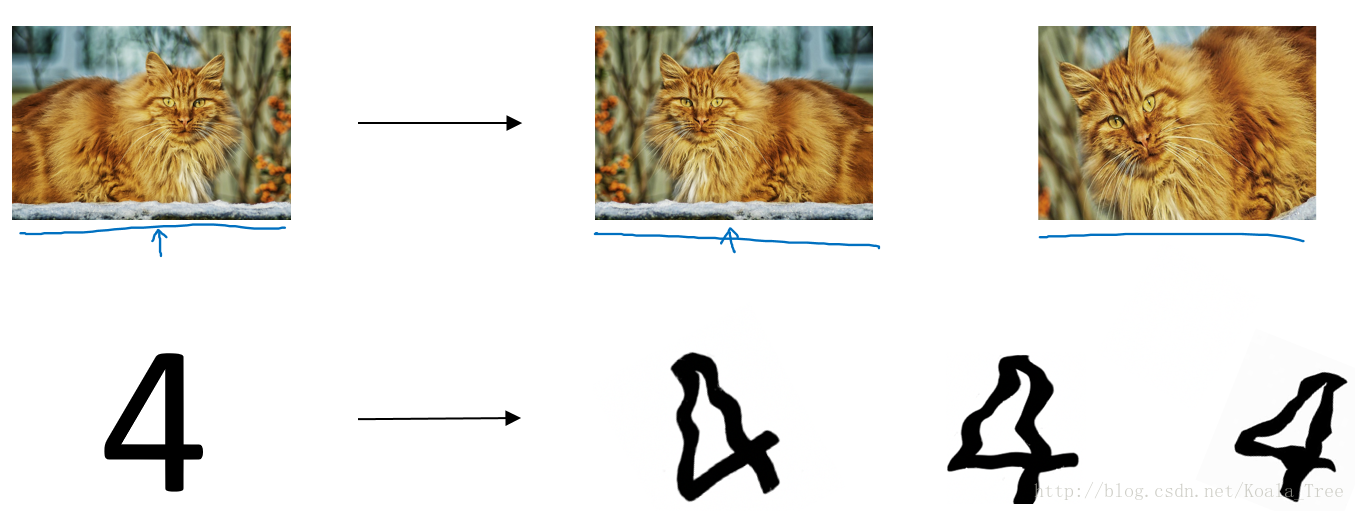
9. 归一化输入
对数据集特征 x 1 , x 2 x_{1},x_{2} x1,x2归一化的过程:
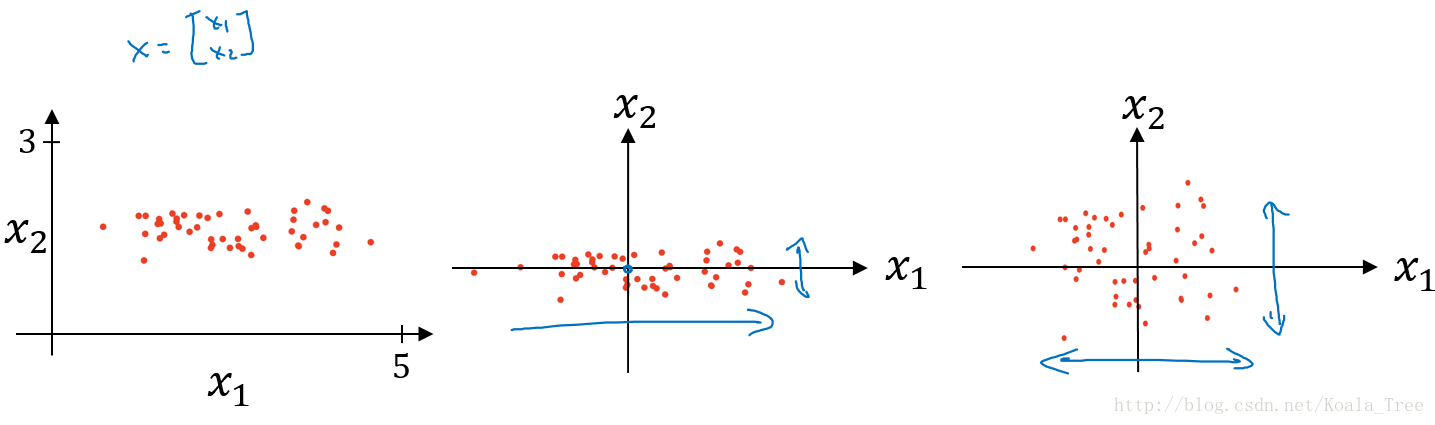
- 计算每个特征所有样本数据的均值: μ = 1 m ∑ i = 1 m x ( i ) \mu = \dfrac{1}{m}\sum\limits_{i=1}^{m}x^{(i)} μ=m1i=1∑mx(i);
- 减去均值得到对称的分布: x : = x − μ x : =x-\mu x:=x−μ;
- 归一化方差: σ 2 = 1 m ∑ i = 1 m x ( i ) 2 \sigma^{2} = \dfrac{1}{m}\sum\limits_{i=1}^{m}x^{(i)^{2}} σ2=m1i=1∑mx(i)2, x = x / σ 2 x = x/\sigma^{2} x=x/σ2
使用归一化的原因:

由图可以看出不使用归一化和使用归一化前后Cost function 的函数形状会有很大的区别。
在不使用归一化的代价函数中,如果我们设置一个较小的学习率,那么很可能我们需要很多次迭代才能到达代价函数全局最优解;如果使用了归一化,那么无论从哪个位置开始迭代,我们都能以相对很少的迭代次数找到全局最优解。
10. 梯度消失与梯度爆炸
如下图所示的神经网络结构,以两个输入为例:
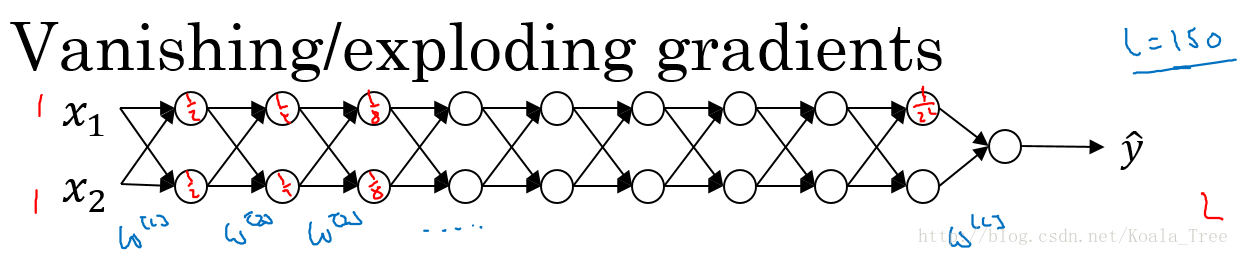
这里我们首先假定 g ( z ) = z , b [ l ] = 0 g(z) = z,b^{[l]}=0 g(z)=z,b[l]=0,所以对于目标输出有:
y ^ = W [ L ] W [ L − 1 ] ⋯ W [ 2 ] W [ 1 ] X \hat y = W^{[L]}W^{[L-1]}\cdots W^{[2]}W^{[1]}X y^=W[L]W[L−1]⋯W[2]W[1]X
-
W
[
l
]
W^{[l]}
W[l]的值大于1的情况:
如: W [ l ] = [ 1.5 0 0 1.5 ] W^{[l]}=\left[\right] W[l]=[1.5 001.5],那么最终, y ^ = W [ L ] [ 1.5 0 0 1.5 ] L − 1 X \hat y = W^{[L]}\left[1.5 001.5 \right]^{L-1}X y^=W[L][1.5 001.5]L−1X,激活函数的值将以指数级递增;1.5 001.5 -
W
[
l
]
W^{[l]}
W[l]的值小于1的情况:
如: W [ l ] = [ 0.5 0 0 0.5 ] W^{[l]}=\left[\right] W[l]=[0.5 000.5],那么最终, y ^ = W [ L ] [ 0.5 0 0 0.5 ] L − 1 X \hat y = W^{[L]}\left[0.5 000.5 \right]^{L-1}X y^=W[L][0.5 000.5]L−1X,激活函数的值将以指数级递减。0.5 000.5
上面的情况对于导数也是同样的道理,所以在计算梯度时,根据情况的不同,梯度函数会以指数级递增或者递减,导致训练导数难度上升,梯度下降算法的步长会变得非常非常小,需要训练的时间将会非常长。
在梯度函数上出现的以指数级递增或者递减的情况就分别称为梯度爆炸或者梯度消失。
11. 利用初始化缓解梯度消失和爆炸问题
以一个单个神经元为例子:
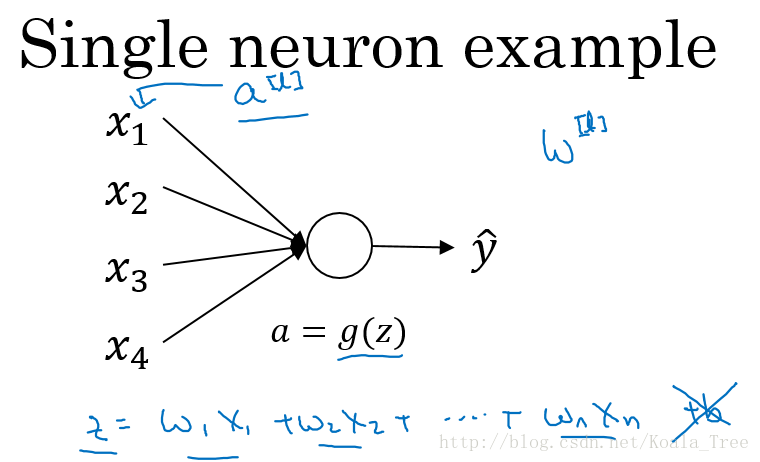
由上图可知,当输入的数量 n n n较大时,我们希望每个 w i w_{i} wi的值都小一些,这样它们的和得到的 z z z也较小。
这里为了得到较小的
w
i
w_{i}
wi,设置
V
a
r
(
w
i
)
=
1
n
Var(w_{i})=\dfrac{1}{n}
Var(wi)=n1,这里称为Xavier initialization。
对参数进行初始化:
WL = np.random.randn(WL.shape[0],WL.shape[1])* np.sqrt(1/n)
- 1
这么做是因为,如果激活函数的输入 x x x近似设置成均值为0,标准方差1的情况,输出 z z z也会调整到相似的范围内。虽然没有解决梯度消失和爆炸的问题,但其在一定程度上确实减缓了梯度消失和爆炸的速度。
不同激活函数的 Xavier initialization:
- 激活函数使用Relu: V a r ( w i ) = 2 n Var(w_{i})=\dfrac{2}{n} Var(wi)=n2
- 激活函数使用tanh: V a r ( w i ) = 1 n Var(w_{i})=\dfrac{1}{n} Var(wi)=n1
其中n是输入的神经元个数,也就是 n [ l − 1 ] n^{[l-1]} n[l−1]。
12. 梯度的数值逼近
使用双边误差的方法去逼近导数:
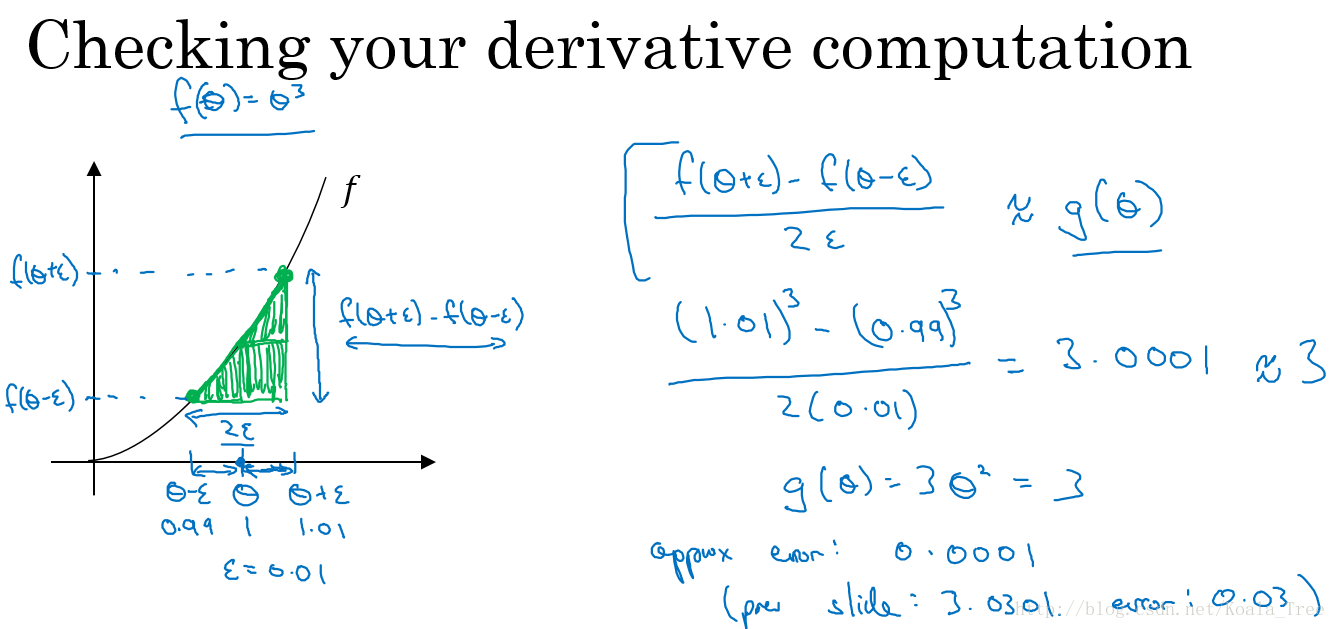
由图可以看出,双边误差逼近的误差是0.0001,先比单边逼近的误差0.03,其精度要高了很多。
涉及的公式:
- 双边导数:
f ′ ( θ ) = lim ε → 0 = f ( θ + ε ) − ( θ − ε ) 2 ε f'(\theta) = \lim\limits_{\varepsilon \to 0}=\dfrac{f(\theta+\varepsilon)-(\theta-\varepsilon)}{2\varepsilon} f′(θ)=ε→0lim=2εf(θ+ε)−(θ−ε)
误差: O ( ε 2 ) O(\varepsilon^{2}) O(ε2) - 单边导数:
f ′ ( θ ) = lim ε → 0 = f ( θ + ε ) − ( θ ) ε f'(\theta) = \lim\limits_{\varepsilon \to 0}=\dfrac{f(\theta+\varepsilon)-(\theta)}{\varepsilon} f′(θ)=ε→0lim=εf(θ+ε)−(θ)
误差: O ( ε ) O(\varepsilon) O(ε)
13. 梯度检验
下面用前面一节的方法来进行梯度检验。
连接参数
因为我们的神经网络中含有大量的参数: W [ 1 ] , b [ 1 ] , ⋯ , W [ L ] , b [ L ] W^{[1]},b^{[1]},\cdots,W^{[L]},b^{[L]} W[1],b[1],⋯,W[L],b[L],为了做梯度检验,需要将这些参数全部连接起来,reshape成一个大的向量 θ \theta θ。
同时对 d W [ 1 ] , d b [ 1 ] , ⋯ , d W [ L ] , d b [ L ] dW^{[1]},db^{[1]},\cdots,dW^{[L]},db^{[L]} dW[1],db[1],⋯,dW[L],db[L]执行同样的操作。
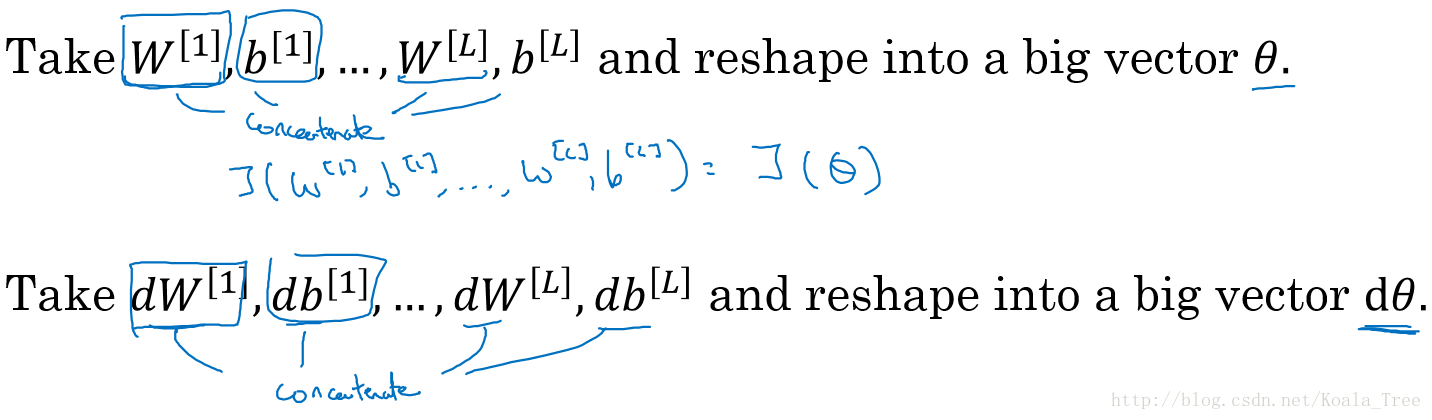
进行梯度检验
进行如下图的梯度检验:

判断 d θ a p p r o x ≈ d θ d\theta_{approx}\approx d\theta dθapprox≈dθ是否接近。
判断公式:
∣
∣
d
θ
a
p
p
r
o
x
−
d
θ
∣
∣
2
∣
∣
d
θ
a
p
p
r
o
x
∣
∣
2
+
∣
∣
d
θ
∣
∣
2
\dfrac {||d\theta_{approx}-d\theta||_{2}}{||d\theta_{approx}||_{2}+||d\theta||_{2}}
∣∣dθapprox∣∣2+∣∣dθ∣∣2∣∣dθapprox−dθ∣∣2
其中,“
∣
∣
⋅
∣
∣
2
||\cdot ||_{2}
∣∣⋅∣∣2”表示欧几里得范数,它是误差平方之和,然后求平方根,得到的欧氏距离。
14. 实现梯度检验 Notes
- 不要在训练过程中使用梯度检验,只在debug的时候使用,使用完毕关闭梯度检验的功能;
- 如果算法的梯度检验出现了错误,要检查每一项,找出错误,也就是说要找出哪个 d θ a p p r o x [ i ] d\theta_{approx}[i] dθapprox[i]与 d θ d\theta dθ的值相差比较大;
- 不要忘记了正则化项;
- 梯度检验不能与dropout同时使用。因为每次迭代的过程中,dropout会随机消除隐层单元的不同神经元,这时是难以计算dropout在梯度下降上的代价函数J;
- 在随机初始化的时候运行梯度检验,或许在训练几次后再进行。(没听懂大师这个点的意思?)
本周(Week4)的课后编程题请参见:


