什么是深度学习？_什么是深度学习csdn

什么是深度学习？

一、什么是深度学习

深度学习没有标准定义，但总的来说，深度学习是机器学习（ML）的一种，主要可以看作是人工神经网络（ANNs）的高级模型。这些技术被用作实现人工智能 (AI) 的工具。
事实上，深度学习从 1950 年代就开始研究。换句话说，深度学习并不是一个新概念，而是一项历史悠久的技术。各时期的主要特点如下：

1950年代出现的感知机可以说是人工神经网络的开端。此后，人工神经网络研究在 1960 年代得到了积极的开展。然而，在 1969 年，一本名为《感知器》的书出版了，它揭示了感知器的致命局限性并包含了证明。然后，在 1970 年代，我们进入了一个黑暗时代，人工神经网络被许多学者所忽视。

1980年代，人工神经网络研究再次开始受到关注。这可以归因于这样一个事实，即在 1986 年设计了一种通过应用误差反向传播来学习多层人工神经网络的方法。在这个时代，深度神经网络 (DNN)、循环神经网络 (RNN) 和卷积神经网络 (CNN) 得到了发展。

在 1990 年代，出现了高级形式的人工神经网络。1997 年发布了高级循环神经网络 LSTM，1998 年发布了高级卷积神经网络 LeNet-5。

2000 年代，人工神经网络以深度学习的名义开始受到关注。知名信息技术研究机构 Gartner 将深度学习列为十大战略技术。

2010 年代，谷歌的 Deep Mind 发布了著名的 AlphaGo。此后，深度学习在韩国受到了爆炸式的关注。

二、深度学习需要解决的问题

分类

找出数据的类别是一个问题。一个例子是根据长度、宽度、高度、车轮尺寸和发动机马力等特征将汽车分为以下类别之一的问题：轻型汽车、半中型汽车、中型汽车和大型汽车。

聚类

这是分组数据实例的问题。换句话说，它是一组具有相似特征的数据实例。例如，查看汽车的长度、宽度、高度、车轮尺寸和发动机马力等特征，并将相似的实例组合在一起。需要人工干预才能将分组结果确定为第 1 组的紧凑型汽车、第 2 组的半紧凑型汽车等。

回归

问题是找出不完整数据的价值。例如，在一个数据实例中，如果您知道汽车的宽度、高度、车轮尺寸和发动机马力等特征，但不知道长度，您可以预测由不完整数据组成的实例的长度特征。关于其他数据实例的值。。

每个问题都可以从机器学习的角度来解决，学习方法又可以分为监督学习、无监督学习和强化学习。

监督学习

它是一种训练标记数据的方法，主要处理分类和回归问题。它相对容易学习和有效，因为有标签意味着有正确的答案。但是，按数据标记通常很昂贵。成本可以是金钱、时间，或者在许多情况下两者兼而有之。训练数据海量，从上亿到上千万，甚至更多。有时人类不可能标记这些数据。

无监督学习

如何训练未标记的数据。主要用于对数据进行分组或分析数据的特征。由于无监督学习正在分析没有正确答案的数据，因此无需标记数据。这意味着准备数据的成本更低。然而，在许多情况下，需要人工干预来确定所分析集群的含义。

三、深度学习发展历程

最近备受关注的深度学习其实有着悠久的历史。本章介绍被认为是深度学习的深度神经网络，从感知机（可以说是深度学习的开端）到高级人工神经网络。

感知机

感知机是弗兰克·罗森布拉特在 1957 年设计的基本人工神经网络。感知机的结构如下图所示。

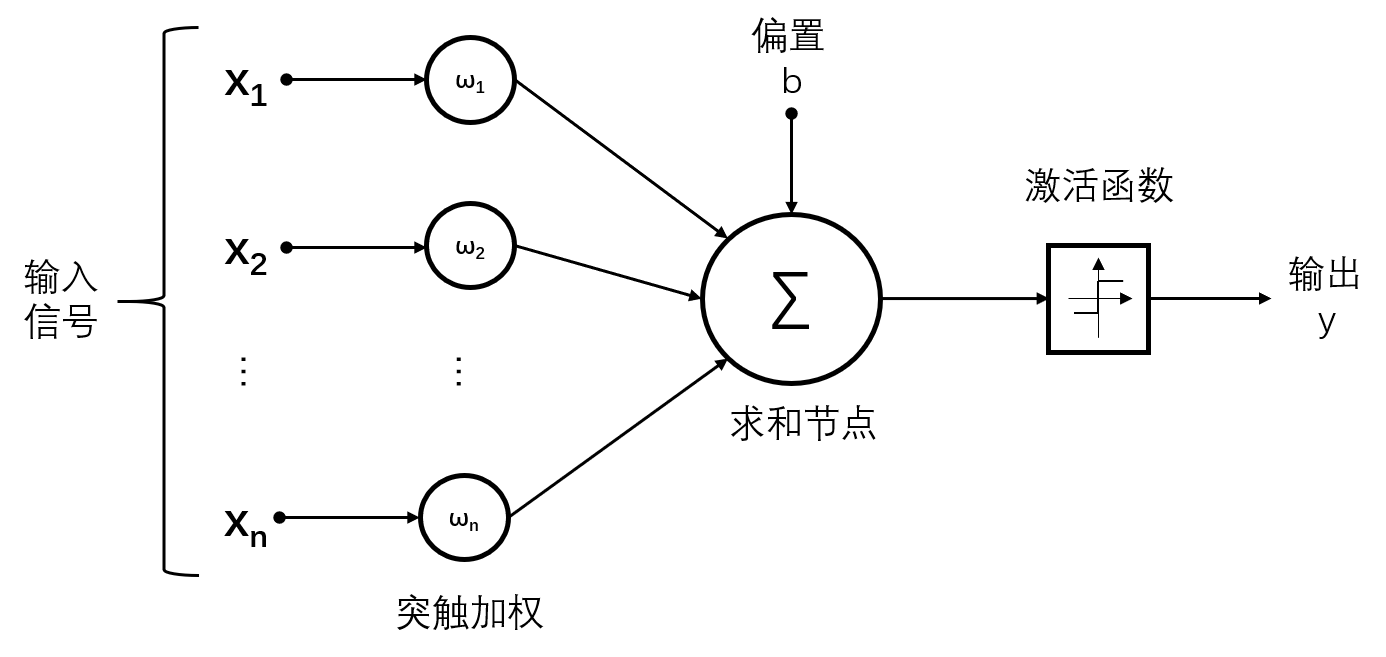
感知器有一个激活函数，如果输入值和偏差值乘以权重并求和，即如果“权重乘积之和”超过阈值，则输出 1，否则输出 0。这里要注意的一件事是输出值为 0 或 1。用公式表示：

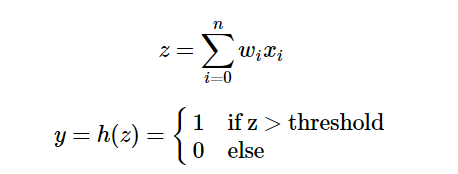
如上所述，但再次使用公式中使用的符号。z 是加权乘积的总和，即输入乘以权重的总和。h(z)是激活函数z如果大于阈值则输出 0，否则输出 0。

X0是偏差值和X一从现在开始，每一个输入值都会被表示出来，让我们看看两者之间有什么区别。输入从外部进入感知机，但偏差是工程师（我们）在构建感知机时设置的值。产生偏差的原因是使阈值为零。设置阈值可能很困难或不可能，而零阈值也可以更容易地实现激活函数。如果bias设置为1，学习过程w0它近似于此（阈值×-1）。

激活函数

人工神经网络是多层感知器的稍微高级一点的模型。神经网络由输入层、隐藏层和输出层组成。
在人工神经网络中，隐藏层中有各种激活函数。
激活功能模拟活神经细胞的突触小泡，当电位超过一定值时，小泡爆裂，成为突触之间的连接，发挥作用。但是，根据激活函数，可能会转换要传递给下一个感知机的值。神经网络的效率取决于激活函数的类型，这与误差反向传播过程中的梯度损失问题有关。如果你有兴趣，请参考人工智能方面的书籍。

阶跃函数

阶跃函数是前面在感知器中讨论的激活函数。如果权重乘积之和小于 0，则感知器中的阶跃函数返回 0，如果大于 0，则返回 1。可以设置step函数返回的不同值。例如，以下公式中的阶跃函数返回 -1 或 1

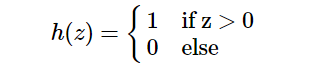
relu 函数

relu 函数是一个激活函数，如果权重乘积之和大于 0，则返回原样，如果小于 0，则返回 0。这可以表示为如下公式：

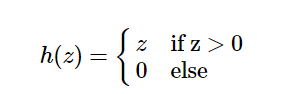
线性函数

线性函数是具有相同输入和输出的线性函数。线性函数的形状实际上就是一条直线。

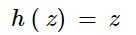
sigmoid函数

sigmoid 函数是一个激活函数，它返回调整为 0 和 1 之间值的权重乘积之和。sigmoid函数也称为逻辑函数，公式如下：

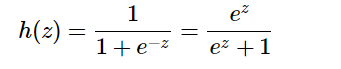
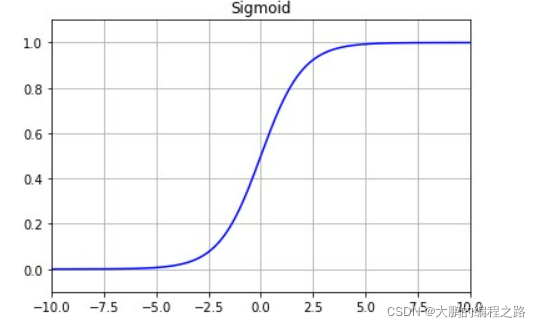
sigmoid函数的特点是，当权重乘积之和从0增加到正或负时，返回的值变化很快，绝对值在2.5以上时变化不大。你可以改变这个 S 形，但是深度学习通常会按原样使用它。

双曲正切函数

双曲正切（tanh 函数）的形状类似于 sigmoid 函数。双曲正切函数返回的值范围从-1到1，当加权乘积之和从0增加到正或负时，变化比sigmoid函数更快。双曲正切函数的公式如下：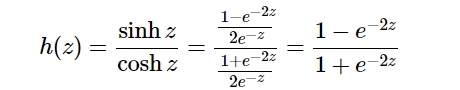
双曲正切函数曲线如下：