llama.cpp 源码解析_llama.cpp 分析

原文出自这里：
CodeLearner

0 前言

1 代码结构&调用流程

1.1 代码结构

1.2 调用流程
1
2
3

2 逐算子解析

2.1 Attention Block

      2.1.1 rms\_norm\_f32

      2.1.2 Linear Linear  

                 \* dequantize Linear

                 * quantize Linear

      2.1.3 rope_f32

      2.1.4 Copy_kernel

      2.1.5 Multi-Head-Attention

      2.1.6 add_f32

2.2 FeedForward Block
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

2.2.1 silu_f32

0 前言

在上一篇文章，我们结合源码一起看了Meta开源的大语言模型llama 2的模型结构细节，并且还在B站录制了一个讲解视频方便大家理解，大家可以先回顾一下

Llama 2详解

B站视频解析Llama2(B站 CodeLearner)

而为了更好的了解llama 2在推理时的算子调用情况，以及大模型在实际推理时一些的瓶颈所在，所以本文继前文之后，选择了一个大模型推理框架llama.cpp 来进一步学习LLM的推理与部署

首先，我们先简单介绍一下llama.cpp：该项目是开发者 Georgi Gerganov 基于 Meta 的 LLaMA 模型 手写的纯 C/C++ 版本：支持CPU推理,当然也支持CUDA/OpenCL推理、具有 FP16 和 FP32 的混合精度、支持8-bit/4bit量化… , 截止当前github stars 数42.2k ，反正火爆的不行，所以本文就记录一下笔者在阅读llama.cpp源码时的一些理解~

同时也给出作者注释后的llama.cpp(https://github.com/sunkx109/llama.cpp)

因为llama.cpp还在一直更新，相应的功能和代码也有一些变动，为了方便大家对照，我选用的是版本为commitID = 097e121e2f17ed3541cf02c55ff7e9febc091b19，当然也有对应的release版本，大家可以至github llama.cpp release-master-097e121下载对应版本。另外，因为llama.cpp支持多平台，而多平台的实现虽然代码有差异，但是功能一致，所以本文就以N卡 CUDA版本为例来进行解析～

因为是llama.cpp的CUDA 后端推理，所以在阅读本文之前有一些先导知识需要了解：

• Llama 2模型的结构要熟悉，这一点可以参考我写的Llama 2详解

• 使用N卡推理，那么CUDA 编程要熟悉，这一点可以参考我写的CUDA编程学习笔记专栏

• 模型量化，大模型的量化推理非常重要，llama.cpp支持多bit量化推理，本文会以8bit推理为例说明。可以参考我写的神经网络量化入门

1 代码结构&调用流程

1.1 代码结构

llama.cpp 的代码结构比较直观，如下所示，为整体代码结构中的比较核心的部分的代码结构

|-- example | |-- main | |-- main.cpp # 推理llama 2的主函数 |-- ggml.c # ggml.c 和.h文件定义一些框架的基础数据结构和函数等 |-- ggml.h |-- ggml-alloc.c #内存分配管理 |-- ggml-alloc.h |-- llama.cpp # 整个llama 2的计算图构建和weight加载等 |-- llama.h |-- ggml-cuda.cu #cuda版本的llama2 中的kernel实现与调用 |-- ggml-cuda.h |-- ggml-opencl.cpp #opencl版本的llama2 中的kernel实现与调用 |-- ggml-opencl.h |-- ... #其他

1.2 调用流程

当我们搭建完成环境，并对llama.cpp 进行编译后 在llama.cpp/build/bin/会生成一个main的可执行文件，根据README.md给的相关命令即可进行llama2的推理。大致梳理一下llama.cpp的调用执行流程:

首先，main这个可执行文件的源码对应于llama.cpp/examples/main/main.cpp，在main.cpp中会解析命令行的参数，如所用的模型文件，prompt信息等，之后进行一系列操作后，用一个llama_token_bos()token并调用了一次llama_eval()函数来对模型进行了一次warm up, 之后进入一个while循环进行模型的推理，期间会多次调用llama_eval()函数进行推理，直到不满足while条件。

llama_eval()函数的定义在llama.cpp/llama.cpp文件中,llama_eval()函数进一步会去调用llama_eval_internal()函数,llama_eval_internal()函数内部会根据预先的宏定义走不同的推理模式，比如GGML_USE_MPI、GGML_USE_MPI和其他模式，因为本文是以CUDA推理模式进行说明的，所以我们主要看该模式下的函数调用：主要有两个 llama_build_graph()和ggml_graph_compute_helper() 。这两个函数的功能分别是前者用于构建推理计算图 ，而后者则是根据计算图调用对应算子

• llama_build_graph

llama_build_graph()函数接口，如下所示

static struct ggml_cgraph * llama_build_graph( llama_context & lctx, //llama context 存放着一些模型信息，包括模型文件、超参数等 const llama_token * tokens, // 需要去处理的tokens const float * embd, //embeddings input int n_tokens, //number of tokens int n_past //已经处理的tokens数量 ) ;

这其中整个llama 2的模型结构的推理计算图全在该函数内实现，代码太长了为了节省篇幅就不截取了，大家可以根据函数名找到对应的函数实现

• ggml_graph_compute_helper

ggml_graph_compute_helper()函数内部主要会调用两个函数: ggml_graph_plan() 和 ggml_graph_compute() 。前者用于创建一个ggml_cplan结构体cplan，同时根据之前llama_build_graph()创建的计算图，对图中每个节点所对应的算子OP确定cplan中的成员值，之后返回cplan。后者根据llama_build_graph()创建的计算图和ggml_graph_plan()创建的cplan 进一步调用ggml_graph_compute_thread,这个函数再根据当前计算图节点信息进一步调用ggml_compute_forward

• ggml_compute_forward

此函数会根据当前节点的信息调用具体的算子。当然根据不同的编译选项会使得算子有不同的调用：当定义了GGML_USE_CUBLAS，如果当前节点所对应的算子在CUDA平台有具体的实现就会调用它，否则就会调用CPU端的实现

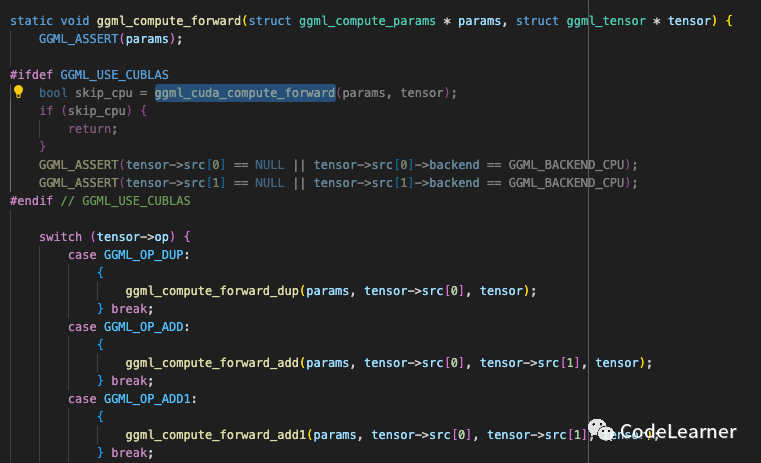
ggml_compute_forward

ggml_cuda_compute_forward 就会调用具体的CUDA节点

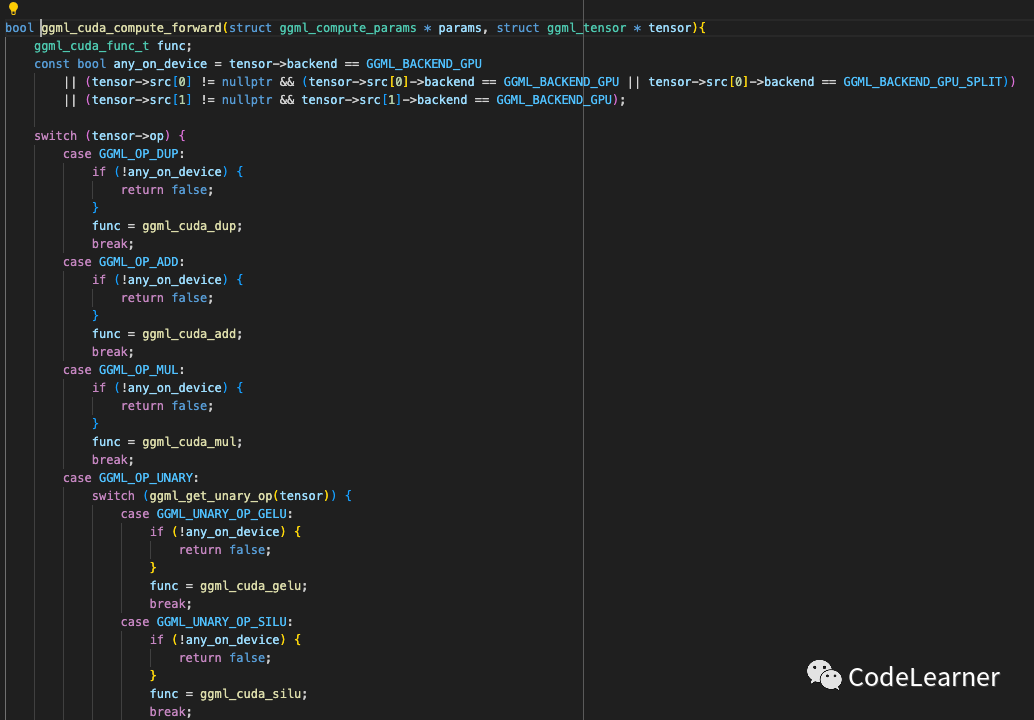
ggml_cuda_compute_forward

另外，整个llama.cpp中一个很重要的结构体ggml_tensor，其定义如下

struct ggml_tensor { enum ggml_type type; //数据类型FP32 INT8等 enum ggml_backend backend; //后端CPU/GPU int n_dims;//几维度 int64_t ne[GGML_MAX_DIMS]; // number of elements，这就是tensor的shape,不过它的存放方式是倒着的 //比如[batch_size,multi-head,seq_len,head-dim] //他的存储方式是ne[0]=head-dim,ne[1]=seq_len,ne[2]=multi-head,ne[3]=batch_size size_t nb[GGML_MAX_DIMS]; // stride in bytes: // nb[0] = sizeof(type) // nb[1] = nb[0] * ne[0] + padding // nb[i] = nb[i-1] * ne[i-1] // compute data enum ggml_op op; // op params - allocated as int32_t for alignment int32_t op_params[GGML_MAX_OP_PARAMS / sizeof(int32_t)]; bool is_param; struct ggml_tensor * grad; struct ggml_tensor * src[GGML_MAX_SRC]; // performance int perf_runs; int64_t perf_cycles; int64_t perf_time_us; void * data; char name[GGML_MAX_NAME]; void * extra; // extra things e.g. for ggml-cuda.cu char padding[4]; };

至此，llama.cpp 在推理llama 2时的一个主要调用逻辑，就算说完了，接下来，我们来看看本文的重点部分：llama 2 中每个Transformer Block的CUDA版本的算子调用及解析

2 逐算子解析

在之前Llama2 详解中我们说过，大模型的推理可以分为prompt和generation两个阶段，两个阶段在处理时的差异在于数据维度的差异，即prompt阶段是多token输入 input_tensor: [batch_size, seq_len, hidden_dim] ; 而generation阶段的输入则是 input_tensor: [batch_size, 1, hidden_dim] ，所以前者更多的计算算子是gemm，而后者更多的计算算子则是gemv 。

后文中为了方便说明具体的参数信息，本文以Llama-2 7B模型 batch_size =1 为例来说明llama.cpp 在推理时的tensor shape和其他参数信息

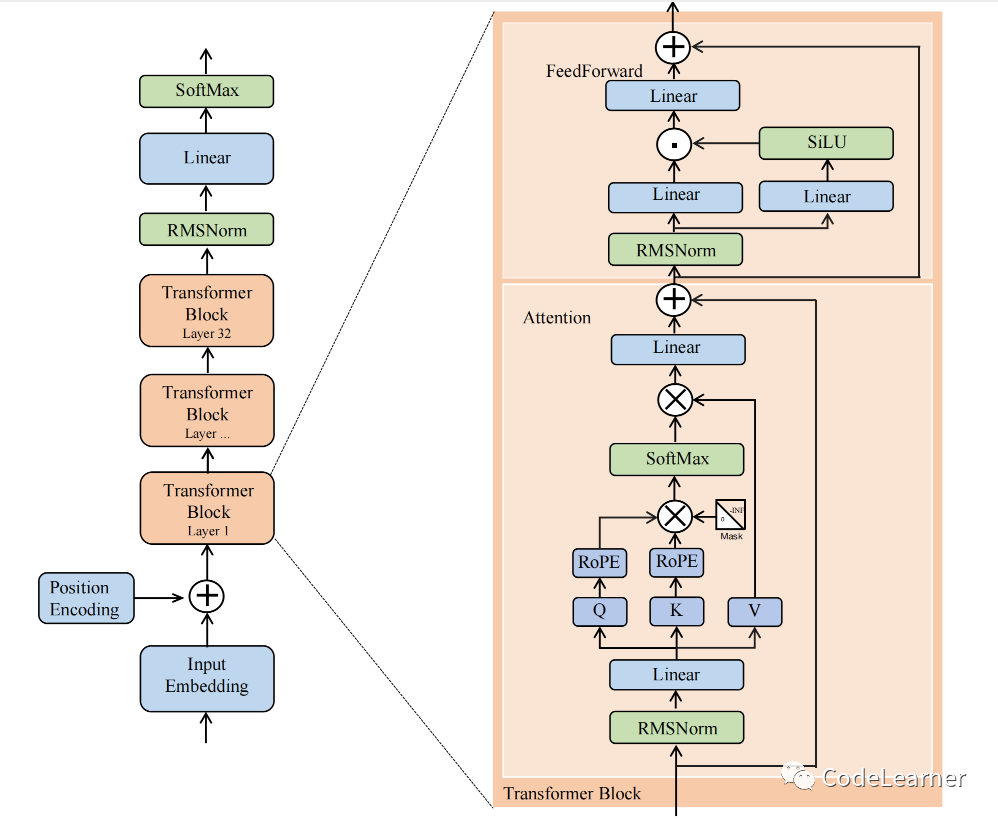
回顾一下，上图为Llama2 详解中我画的llama 2的模型结构图。根据模型结构，我们来看看llama.cpp的推理流程。如下图所示，为我通过Nsight Systems工具抓取的 在llama.cpp 选用CUDA作为推理后端时的算子调用和执行情况，其中黄色框为一次warmup，绿色框就是prompting阶段，红色框的多个块就是一次次的generation阶段。相信大家也不难发现，通过Nsight Systems所统计的执行时间占比最大的kernel是dequantize_mul_mat_vec——简单解释一下：这是一个反量化矩阵向量乘法，只会在generation阶段调用。所以说大模型的推理，generation阶段占比更重，红色框中的一个小块即为生成一个token所调用kernel的时间，而随着你需要生成的token的数量增多，红色框的占比会越来越大。

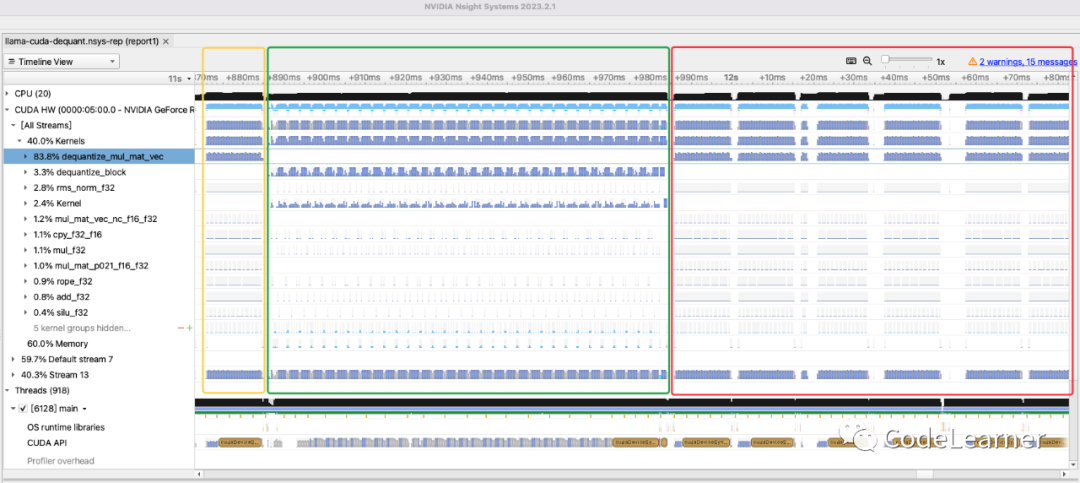
那么接下来，我们就结合上述模型结构图和Nsight Systems 截图来一起看看llama 2推理时都会调用哪些CUDA算子，以及llama.cpp 对这些算子是如何实现的～

因为prompting和generation只是在tensor shape不一样，而算子实现的算法功能都是一致的。那么我们可以根据llama 2的模型结构图中将一个Transformer Block拆分为的两个块（Attention Block和FeedForward Block），然后逐一比较这两个块在提示（prompting）和生成（generation）阶段所调用的算子以及它们的实现。

2.1 Attention Block

通过对Nsight Systems Profile report文件放大后分析，可以得到Attention Block的上层算法流程以及其在prompting阶段和generation阶段所调用的CUDA算子，如下图所示。根据这一对比示意图，我们就来细看一下每个算子的功能以及具体的实现

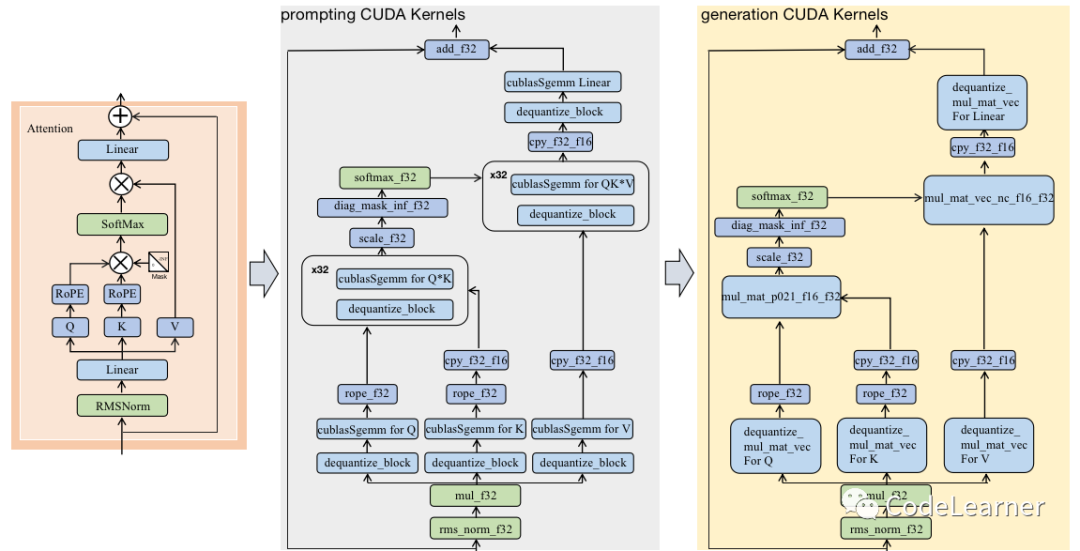
2.1.1 rms_norm_f32

我们回忆一下RMS Norm的公式：

其中 为可学习的参数，推理时固定

`#define WARP_SIZE 32  
//call kernel  
static void rms_norm_f32_cuda(const float * x, float * dst, const int ncols, const int nrows, const float eps, cudaStream_t stream) {  
    GGML_ASSERT(ncols % WARP_SIZE == 0);  
    const dim3 block_dims(WARP_SIZE, 1, 1); //(32,1,1)  
    //所以调用的cuda的gridDim =(nrows,1,1) ,blockDim = (32,1,1)  
    //也就是说一个block处理一个row的数据，即每32个线程处理一行数据 ，共计nrows行  
    rms_norm_f32<<<nrows, block_dims, 0, stream>>>(x, dst, ncols, eps);  
}

//kernel code  
static __global__ void rms_norm_f32(const float * x, float * dst, const int ncols, const float eps) {  
    const int row = blockIdx.x*blockDim.y + threadIdx.y;  
    const int tid = threadIdx.x;

    float tmp = 0.0f; // partial sum for thread in warp  
    //一个线程求和(ncols/WARP_SIZE)个数据的x^2   
    for (int col = tid; col < ncols; col += WARP_SIZE) {  
        const float xi = x[row*ncols + col];  
        tmp += xi * xi;  
    }

        // sum up partial sums  
    // 一个线程束(32个线程)内的归约求和  
#pragma unroll  
    for (int mask = 16; mask > 0; mask >>= 1) {  
        tmp += __shfl_xor_sync(0xffffffff, tmp, mask, 32);  
    }

        const float mean = tmp / ncols; // mean(x^2)  
    const float scale = rsqrtf(mean + eps); // 1/根号mean  
    //算完之后写回原数组  
    for (int col = tid; col < ncols; col += WARP_SIZE) {  
        dst[row*ncols + col] = scale * x[row*ncols + col];  
    }  
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

所以，rms_norm_f32这个kernel就是在计算RMS Norm的前一部分，之后再通过如下kernel mul_f32乘上 ，就得到了完整的RMS Norm。rms_norm_f32这个kernel 在prompting阶段处理的tensor shape 是[1, seq_len , 4096] ，nrows 等于seq_len，在generation阶段处理的tensor shape 则是[1, 1 , 4096] 。

batch_size =1 ,7B模型的 hidden_dim = 4096

`#define CUDA_MUL_BLOCK_SIZE 256  
//call kernel  
static void mul_f32_cuda(const float * x, const float * y, float * dst, const int kx, const int ky, cudaStream_t stream) {  
    const int num_blocks = (kx + CUDA_MUL_BLOCK_SIZE - 1) / CUDA_MUL_BLOCK_SIZE;  
    mul_f32<<<num_blocks, CUDA_MUL_BLOCK_SIZE, 0, stream>>>(x, y, dst, kx, ky);  
}

//kernel  
static __global__ void mul_f32(const float * x, const float * y, float * dst, const int kx, const int ky) {  
    const int i = blockDim.x*blockIdx.x + threadIdx.x;

    if (i >= kx) {  
        return;  
    }  
    dst[i] = x[i] * y[i%ky];  
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

mul_f32算子比较简单就是挨个元素乘上对应的 ，其实rms_norm_f32和mul_f32 可以合并成一个kernel，后续文章会推出一些kernel优化的解析会讲到。

2.1.2 Linear Layer

对比Llama 2模型结构可以发现，一个Transformer Block中总共有7个Linear层：生成Q、K、V的三个Linear、Attention Block中最后一个Linear和FeedForward Block中的3个Linear。虽然这些Linear层处理的tensor 的shape是不同的，但是在相同的阶段调用的算子都是同一个，所以可以举一反三。

此外，llama.cpp中涉及到量化推理的主要就是Linear层，前文提过本文先导知识之一就是模型量化，所谓模型量化就是将模型中的weight数据和input-tensor数据，通过量化算法将原始FP32类型逻辑等价地转换为int8以及更低bit数据，这样做的好处就是在对模型进行推理时能节省内存和计算加速的好处。模型量化算法有很多种，以常见的对称均匀量化为例，模型量化时都会对原始FP32数据在pre-tensor/pre-channel域计算得到一个scale，然后通过量化公式：将数据由FP32量化为INT-8(或更低bit)数据 。

这里解释一下：模型量化后计算速度的加快的主要原因在于：在同等带宽的情况下能一次向量化的load更多数据(比如原始load 1个FP32的时间 现在能load 4个int8的数据)

以llama.cpp 提供的LLaMA 2 7B chat 8bit模型为例，Llama 2中Linear层的weight数据就是int-8类型，更具体的说，Linear层中的weight数据是以如下结构体的形式保存的，其中d为前文中提到的量化算法中的scale，int8_t qs[QK8_0] 即为量化后的INT-8数据

`#define QK8_0 32  
typedef struct {  
    half    d;              // delta 量化的scale  
    int8_t  qs[QK8_0];      // quants 量化的weight数据  
} block_q8_0;  
`

1
2
3
4
5
6
7

这里的量化scale既不是以pre-tensor为单位也不是以pre-channel为单位，而是以32为单位，主要原因是因为CUDA 一个warp就是32个线程

Linear层在进行量化推理时可以选用两种方式：

1. 反量化int-8的weight，之后将fp32的input-tensor与fp32的weight进行Linear层的运算

2. 量化input-tensor，之后将int-8的input-tensor与int-8的weight进行Linear层的运算

接下来，我们就来看看llama.cpp对于这两种方式是如何实现的

dequantize Linear

首先，对于Linear层prompting阶段和generation阶段都会被调用，但是因为处理的tensor的shape不一样，所以在不同阶段执行时调用的kernel不一样，而在同一个阶段调用的kernel又是一样的，所以为了节省篇幅，后文在讲解时会挑选每个阶段的其中一个Linear层来进行说明。

以反量化的dequantize Linear推理时，在prompting阶段是使用dequantize_block+cublasSgemm实现的，其中前者是一个反量化kernel，将weight反量化为FP32 ，后者就是直接调库的gemm，没啥好说的。所以我们主要来看看generation阶段的实现。前面说过生成阶段处理的tensor shape相对于prompting阶段不同，在generation阶段 以生成Q K V的Linear层为例，其input tensor 's shape 是[batch_size, 1 , hidden_dim] ,而weight还是一个矩阵数据，所以此时llama.cpp会去调用矩阵向量乘法的kernel，具体而言就是 dequantize_mul_mat_vec, 如下图为Nsight 抓取的generation阶段生成QKV的三个Linear的调用情况

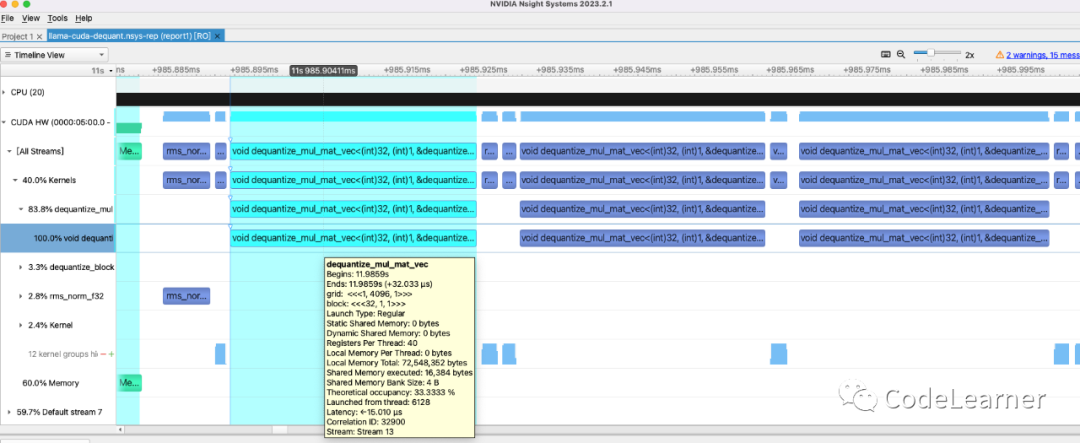
dequantize-linear

具体的核函数调用函数和kernel代码如下所示。这三个Linear 调用的都是dequantize_mul_mat_vec算子，girdDim=(1,4096,1) ，blockDim=(32,1,1) ，输入tensor shape是[1, 1, 4096]，而weight shape则是[1, 4096 , 4096]，所以CUDA kernel用了4096个block来处理整个gemv，每个block处理一行的weight * input tensor。

input tensor shape和weight shape依然是以Llama-2 7B模型，batch_size = 1 为例说明

又因为weight是以结构体的方式存储的32个weight数据共享一个scale数据，所以结构体的数量为(4096 * 4096 / 32)。kernel的具体写法在以下代码块中做了详细注释。

dequantize_mul_mat_vec的gridDim = {1,4096,1} , blockDim = {32,1,1}，也就说对于[1,4096] * [4096,4096]的矩阵向量乘，一共用了4096个block来处理，每个block中32个线程，每个block处理中的线程处理一个[1,4096] * [1,4096]的逐元素乘后累和。

`//call kernel  
#define QK8_0 32  
#define QR8_0 1  
static void dequantize_mul_mat_vec_q8_0_cuda(const void * vx, const dfloat * y, float * dst, const int ncols, const int nrows, cudaStream_t stream) {  
    GGML_ASSERT(ncols % GGML_CUDA_DMMV_X == 0);  
    const int block_num_y = (nrows + GGML_CUDA_MMV_Y - 1) / GGML_CUDA_MMV_Y;  
    const dim3 block_nums(1, block_num_y, 1); // (1,4096,1)  
    const dim3 block_dims(WARP_SIZE, GGML_CUDA_MMV_Y, 1);  //(32,1,1)  
    dequantize_mul_mat_vec<QK8_0, QR8_0, dequantize_q8_0>  
        <<<block_nums, block_dims, 0, stream>>>(vx, y, dst, ncols, nrows);  
}

//kernel code  
static __device__ __forceinline__ void dequantize_q8_0(const void * vx, const int ib, const int iqs, dfloat2 & v){  
    //因为此时的int8量化是采用的是均匀对称量化  
    //根据量化公式，反量化就是int8 * scale  
    const block_q8_0 * x = (const block_q8_0 *) vx;

    const dfloat d = x[ib].d; //scale

    v.x = x[ib].qs[iqs + 0]; //int8 weight   
    v.y = x[ib].qs[iqs + 1]; //int8 weight 

#ifdef GGML_CUDA_F16  
    //FP16的情况  
    v = __hmul2(v, {d, d});  
#else  
    //FP32的情况  
    v.x *= d; //反量化  
    v.y *= d; //反量化  
#endif // GGML_CUDA_F16  
}

//gridDim = {1,4096,1} , blockDim = {32,1,1}

template <int qk, int qr, dequantize_kernel_t dequantize_kernel>  
static __global__ void dequantize_mul_mat_vec(const void * __restrict__ vx, const dfloat * __restrict__ y, float * __restrict__ dst, const int ncols, const int nrows) {  
    // qk = quantized weights per x block  
    // qr = number of quantized weights per data value in x block

      const int row = blockIdx.y*blockDim.y + threadIdx.y;  //0-4095

    if (row >= nrows) {  
        return;  
    }

    const int tid = threadIdx.x; //0-31

    const int iter_stride = 2*GGML_CUDA_DMMV_X; // 2 * 32  
    const int vals_per_iter = iter_stride / WARP_SIZE; //2  num quantized vals per thread and i iter  
                                                       //单个线程，for循环的一次迭代所处理的数据量--2  
    const int y_offset = qr == 1 ? 1 : qk/2; // 1

// partial sum for each thread  
#ifdef GGML_CUDA_F16  
    half2 tmp = {0.0f, 0.0f}; // two sums for f16 to take advantage of half2 intrinsics  
#else  
    float tmp = 0.0f;  
#endif // GGML_CUDA_F16  
    //32个线程需要处理4096组数据的乘加

        for (int i = 0; i < ncols; i += iter_stride) {  
        const int col = i + vals_per_iter*tid; //列坐标，因为一个线程一次for循环迭代处理两个数据，所以32个线程一次迭代可以处理64个数据  
        const int ib = (row*ncols + col)/qk; // x block index ，就是weight数据的第几个block结构体  
        const int iqs = (col%qk)/qr; // x quant index，当前列坐标所对应的weight数据block结构体内部的第几个索引  
        const int iybs = col - col%qk; // y block start index，与当前weight数据block 对应的input_tensor的起始index

// processing >2 values per i iter is faster for fast GPUs  
        //前面说过一个线程每次迭代都处理两个数据，向量化存取有效利用量化所节省的带宽  
#pragma unroll  
        for (int j = 0; j < vals_per_iter; j += 2) {  
            // process 2 vals per j iter

            // dequantize  
            // for qr = 2 the iqs needs to increase by 1 per j iter because 2 weights per data val  
            dfloat2 v; //float2类型，就是两个float  
            dequantize_kernel(vx, ib, iqs + j/qr, v); //反量化之后的数据存到v

            // matrix multiplication  
            // for qr = 2 the y index needs to increase by 1 per j iter because of y_offset = qk/2  
#ifdef GGML_CUDA_F16  
            tmp += __hmul2(v, {  
                y[iybs + iqs + j/qr + 0],  
                y[iybs + iqs + j/qr + y_offset]  
            });  
#else  
            //两个数据分别相乘后相加  
            tmp += v.x * y[iybs + iqs + j/qr + 0];   
            tmp += v.y * y[iybs + iqs + j/qr + y_offset];  
#endif // GGML_CUDA_F16  
        }  
    }

    // sum up partial sums and write back result  
    //对每个block中的tmp进行累和，即为每一行weight与input_tensor进行乘加后的结果  
#pragma unroll  
    for (int mask = 16; mask > 0; mask >>= 1) {  
        tmp += __shfl_xor_sync(0xffffffff, tmp, mask, 32);  
    }  
    //当tid=0时再把每个block的结果写会结果  
    if (tid == 0) {  
#ifdef GGML_CUDA_F16  
        dst[row] = tmp.x + tmp.y;  
#else  
        dst[row] = tmp;  
#endif // GGML_CUDA_F16  
    }  
}

`
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110

quantize Linear

Linear层的第二种调用方式就是对输入tensor做量化，之后再与int8的weight做int8的运算。同样，我们以generation阶段的生成QKV的三个Linear之一为例的实现进行说明。通过Nsight 抓取的kernel 调用情况可以发现，每个mul_mat_vec_q在被调用之前，都会有一个quantize_q8_1 ，quantize_q8_1用于对输入tensor进行量化，mul_mat_vec_q则是进行int8的矩阵向量乘法。前面说过此时的输入tensor shape是[1, 1, 4096]，weight shape是[1, 4096 , 4096]，其中weight的数据依然是采用block_q8_0这种结构体的方式存储。

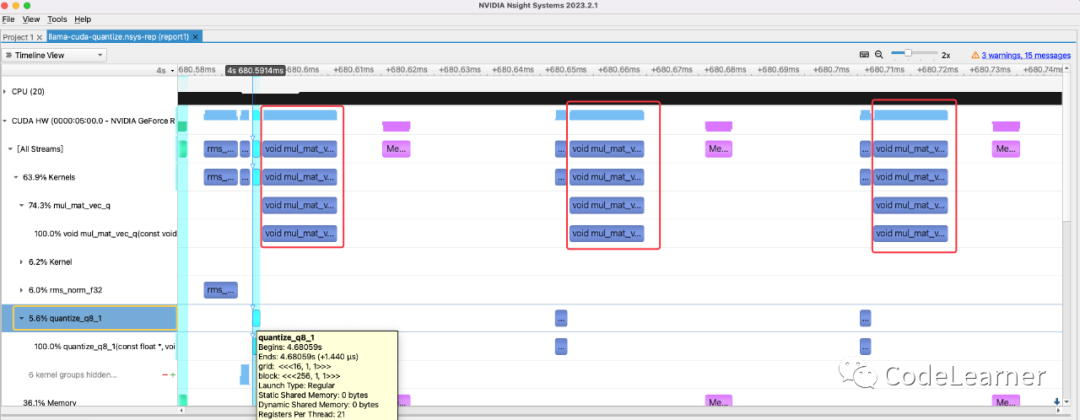
quantize-linear

具体的kernel实现和调用如下

• 量化函数 ——quantize_q8_1

quantize_q8_1 kernel用于对数据进行int8的对称均匀量化，具体而言，此时就是对输入shape为[1,1,4096]的fp32数据进行量化，girdDim ={16,1,1} , blockDim={256 , 1, 1}

16 * 256 = 4096，实际就是一个线程量化一个数据

`#define QK8_1 32  
typedef struct {  
    half2   ds;             // ds.x = delta, ds.y = sum ，这里的ds存了两个half 第一个half是scale，第二half是sum  
    int8_t  qs[QK8_0];      // quants ，int8 数据  
} block_q8_1;  
static __global__ void quantize_q8_1(const float * __restrict__ x, void * __restrict__ vy, const int kx, const int kx_padded) {  
    const int ix = blockDim.x*blockIdx.x + threadIdx.x; //0-4096

    if (ix >= kx_padded) {  
        return;  
    }  
    const int iy = blockDim.y*blockIdx.y + threadIdx.y; //0  
    const int i_padded = iy*kx_padded + ix; //ix  
    block_q8_1 * y = (block_q8_1 *) vy; 

    const int ib = i_padded / QK8_1; // block index  因为结构体数据是以32为一组，所以ib计算得到当前数据所在结构体block的index  
    const int iqs = i_padded % QK8_1; // quant index iqs计算的就是当前数据所在结构体内部的index

    const float xi = ix < kx ? x[iy*kx + ix] : 0.0f; //防止超出  
    float amax = fabsf(xi); // 当前数据的绝对值  
    float sum = xi;

       //一个block内部既做归约求和也做归约求最大值  
#pragma unroll  
    for (int mask = 16; mask > 0; mask >>= 1) {  
        amax = fmaxf(amax, __shfl_xor_sync(0xffffffff, amax, mask, 32));  
        sum += __shfl_xor_sync(0xffffffff, sum, mask, 32);  
    }  
    //套用均匀对称量化的量化公式  
    //q = round(clip(r_i /scale,Q_{min},Q_{max}))  
    //scale = fmax-fmin/qmax-qmin   
    const float d = amax / 127;  
    const int8_t q = amax == 0.0f ? 0 : roundf(xi / d);  
    //存储量化后的值  
    y[ib].qs[iqs] = q;

      if (iqs > 0) {  
        return;  
    }  
    //只用iqs==0的线程将scale和sum写回  
    y[ib].ds.x = d;  
    y[ib].ds.y = sum;  
}

`
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

• 量化的矩阵向量乘——mul_mat_vec_q

对input_tensor调用了量化函数之后，再调用mul_mat_vec_q执行int8的输入与int8的weight之间的矩阵向量乘法运算，mul_mat_vec_q的gridDim = {1,4096,1} blockDim ={32,1,1}，所以同样是每个block处理一行的weight与input_tensor做乘加运算，一共4096行。每个block内部32个线程又处理4096个数据的乘加运算

`#define VDR_Q8_0_Q8_1_MMVQ 2  
static void mul_mat_vec_q8_0_q8_1_cuda(const void * vx, const void * vy, float * dst, const int ncols, const int nrows, cudaStream_t stream) {  
    GGML_ASSERT(ncols % QK8_0 == 0);  
    const int block_num_y = (nrows + GGML_CUDA_MMV_Y - 1) / GGML_CUDA_MMV_Y;  
    const dim3 block_nums(1, block_num_y, 1);  
    const dim3 block_dims(WARP_SIZE, GGML_CUDA_MMV_Y, 1);  
    //QK8_0 =32 ,QI8_0 = 8  
    mul_mat_vec_q<QK8_0, QI8_0, block_q8_0, VDR_Q8_0_Q8_1_MMVQ, vec_dot_q8_0_q8_1>  
        <<<block_nums, block_dims, 0, stream>>>(vx, vy, dst, ncols, nrows);  
}  
template <int vdr> static __device__ __forceinline__ float vec_dot_q8_0_q8_1_impl(  
    const int * v, const int * u, const float & d8_0, const float & d8_1) {  
#if __CUDA_ARCH__ >= MIN_CC_DP4A // lowest compute capability for integer intrinsics  
    int sumi = 0;  
#pragma unroll  
    for (int i = 0; i < vdr; ++i) {  
        // SIMD dot product of quantized values  
        sumi = __dp4a(v[i], u[i], sumi);  
    }  
    return d8_0*d8_1 * sumi;  
#else  
    assert(false);  
    return 0.0f; // only to satisfy the compiler  
#endif // __CUDA_ARCH__ >= MIN_CC_DP4A  
}  
static __device__ __forceinline__ float vec_dot_q8_0_q8_1(  
    const void * __restrict__ vbq, const block_q8_1 * __restrict__ bq8_1, const int & iqs) {

    const block_q8_0 * bq8_0 = (const block_q8_0 *) vbq;

    int v[VDR_Q8_0_Q8_1_MMVQ];  
    int u[VDR_Q8_0_Q8_1_MMVQ];

#pragma unroll  
    for (int i = 0; i < VDR_Q8_0_Q8_1_MMVQ; ++i) {  
        v[i] = get_int_from_int8(bq8_0->qs, iqs + i); //？  
        u[i] = get_int_from_int8_aligned(bq8_1->qs, iqs + i);  
    }

    return vec_dot_q8_0_q8_1_impl<VDR_Q8_0_Q8_1_MMVQ>(v, u, bq8_0->d, bq8_1->ds.x);  
}

//gridDim = {1,4096,1} blockDim ={32,1,1}  
//qk = 32 ， qi = 8 ， block_q_t=block_q8_0，vdr = 2， vec_dot_q_cuda = vec_dot_q8_0_q8_1  
template <int qk, int qi, typename block_q_t, int vdr, vec_dot_q_cuda_t vec_dot_q_cuda>  
static __global__ void mul_mat_vec_q(const void * __restrict__ vx, const void * __restrict__ vy, float * __restrict__ dst, const int ncols, const int nrows) {  
    const int row = blockIdx.y*blockDim.y + threadIdx.y; //the index of row

    if (row >= nrows) {  
        return;  
    }  
    const int blocks_per_row = ncols / qk; //4096 /32 = 128 一行数据共有128个block_q8_0的结构体  
    const int blocks_per_warp = vdr * WARP_SIZE / qi; // 2*32/8 = 8  一个warp一次处理8个block_q8_0的结构体  
                                                      // 所以，每轮迭代4个线程处理一个block_q8_0的结构体  
                                                      // 所以，每轮迭代每个线程处理8个int8数据

   // partial sum for each thread  
    float tmp = 0.0f;  
    //block_q_t = block_q8_0  
    const block_q_t  * x = (const block_q_t  *) vx;  //weight 所对应的结构体指针数据  
    const block_q8_1 * y = (const block_q8_1 *) vy;  //量化input_tensor的结构体指针  
    //根据之前的关系，所以每个线程需要迭代128 / 8 =16次  
    for (int i = 0; i < blocks_per_row; i += blocks_per_warp) {  
        //weight数据 结构体指针block的索引  
        //row*blocks_per_row是当前row的block index  ，i，  
        const int ibx = row*blocks_per_row + i + threadIdx.x / (qi/vdr); // x block index

              //input_tensor数据 结构体指针block的索引，是与weight数据对齐的  
        const int iby = (i + threadIdx.x / (qi/vdr)) * (qk/QK8_1); // y block index that aligns with ibx  
        //iqs = [0 ，2，4，6]   
        const int iqs  = vdr * (threadIdx.x % (qi/vdr)); // x block quant index when casting the quants to int  
        //按照之前的说法，应该是一个线程处理8个数据，但是感觉这里的iqs应该没有办法覆盖到8个数据吧？  
        //大家能解答我的疑惑，还请不吝赐教  
        tmp += vec_dot_q_cuda(&x[ibx], &y[iby], iqs);   
    }

    // sum up partial sums and write back result  
    //对一个block内部求和  
#pragma unroll  
    for (int mask = 16; mask > 0; mask >>= 1) {  
        tmp += __shfl_xor_sync(0xffffffff, tmp, mask, 32);  
    }  
    //结果写回  
    if (threadIdx.x == 0) {  
        dst[row] = tmp;  
    }  
}

`
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89

2.2.3 rope_f32

前文Llama 2详解 对rope 这种位置编码的方式说明过，我们这里在回忆一下rope的公式

对于rope的处理，只会对Q和K进行位置编码，通过Nsight 抓取的kernel调用也能发现

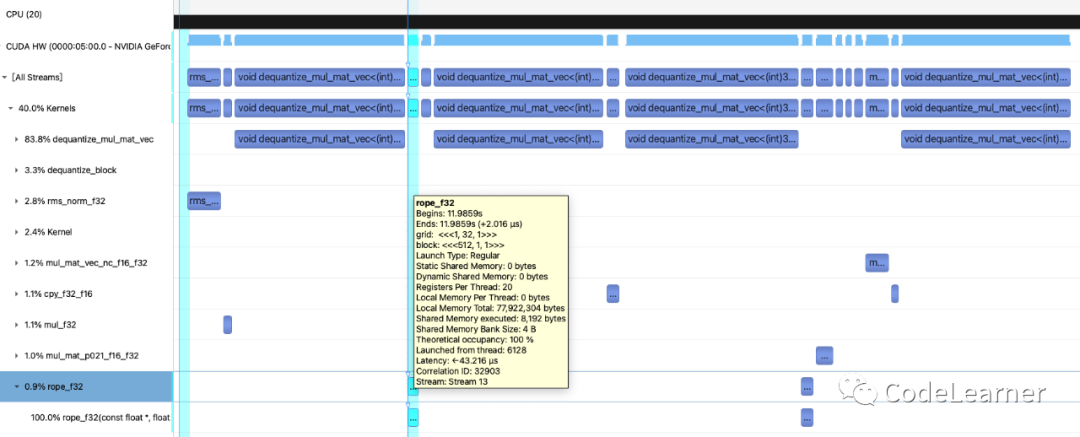
rope

`//(1,32,1)  (512 ,1,1)  
static __global__ void rope_f32(const float * x, float * dst, const int ncols, const float p0,  
                                const float p_delta, const int p_delta_rows, const float theta_scale) {

      const int col = 2*(blockDim.x*blockIdx.x + threadIdx.x); //0-1022  
    //ncols =128  
    if (col >= ncols) {  
        return;  
    }  
    //做了截断所以col的值域为{0，2，4...126}   
    //其实这里不是太懂为什么要512个线程处理，然后又做截断，实际每个block只有64个线程进行了后续运算  
    const int row = blockDim.y*blockIdx.y + threadIdx.y; //0-31  
    const int i = row*ncols + col; //数据的索引  
    //p0 = n_past 就是在生成当前token之前已处理的token长度  
    //p_delta = 1.0  
    //theta_scale = 0.865964  
    //p_delta_rows = 32  
    const float theta = (p0 + p_delta * (row/p_delta_rows))*powf(theta_scale, col/2);  
    const float sin_theta = sinf(theta);  
    const float cos_theta = cosf(theta);

    const float x0 = x[i + 0];  
    const float x1 = x[i + 1];  
    //这里用了32个block处理32个头的rope计算  
    //其中每个block中又只有64   
    dst[i + 0] = x0*cos_theta - x1*sin_theta;  
    dst[i + 1] = x0*sin_theta + x1*cos_theta;  
}

`
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

2.1.4 Copy Kernel

我们之前说过，无论在prompting阶段还是generation阶段，生成的K和V都是要缓存下来的，区别在于prompting阶段是将提示token对应的KV直接写入，而generation阶段则是将单个token对应的KV追加至KV cache。在对K V缓存时，可以直接对FP32数据进行缓存，也可以通过将FP32数据转换为FP16之后再进行缓存，后者虽然会损失一定的精度，但是节省了显存。如下两个kernel用于对数据类型进转换

llama.cpp 中会提前为KV cache分配显存空间，然后prompting阶段和generation阶段生成的KV都会写入。如当最大context大小设置为512时，以FP32为例，每一个Transformer Block会分别给K cache 和 V cache分配512 * 4096 * 4 = 8MB 的存储空间，KV cache一共16MB，那么32个Transformer Block一共512 MB的 KV cache空间。如果使用FP16缓存，则KV cache空间减半

`//fp32 -> fp32  
static __device__ void cpy_1_f32_f32(const char * cxi, char * cdsti) {  
    const float * xi = (const float *) cxi;  
    float * dsti = (float *) cdsti;

    *dsti = *xi;  
}  
//fp32 -> fp16  
static __device__ void cpy_1_f32_f16(const char * cxi, char * cdsti) {  
    const float * xi = (const float *) cxi;  
    half * dsti = (half *) cdsti;

    *dsti = __float2half(*xi); //通过内置函数将数据从fp32转换为fp16  
}

`
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

cpy_f32_f16就是实际的显存拷贝核函数，通过上述的两个kernel的调用将数据拷贝至fp32或fp16。

`template <cpy_kernel_t cpy_1>  
static __global__ void cpy_f32_f16(const char * cx, char * cdst, const int ne,  
                                   const int ne00, const int ne01, const int nb00, const int nb01, const int nb02,  
                                   const int ne10, const int ne11, const int nb10, const int nb11, const int nb12) {  
    const int i = blockDim.x*blockIdx.x + threadIdx.x;

    if (i >= ne) {  
        return;  
    }  
    // determine indices i02/i12, i01/i11, i00/i10 as a function of index i of flattened tensor  
    // then combine those indices with the corresponding byte offsets to get the total offsets  
    // 结合之前的ggml_tensor的ne 和 nb的定义  
    // nb[i] = nb[i-1] * ne[i-1] , nb[0] =sizeof(type)

      const int i02 = i / (ne00*ne01); //the index of ne02   
    const int i01 = (i - i02*ne01*ne00) / ne00; //the index of ne01   
    const int i00 = i - i02*ne01*ne00 - i01*ne00; //the index of ne00  
    const int x_offset = i00*nb00 + i01*nb01 + i02*nb02; //计算偏移

       const int i12 = i / (ne10*ne11); //dst同上  
    const int i11 = (i - i12*ne10*ne11) / ne10;  
    const int i10 = i - i12*ne10*ne11 - i11*ne10;  
    const int dst_offset = i10*nb10 + i11*nb11 + i12*nb12;

    cpy_1(cx + x_offset, cdst + dst_offset); //将cx[x_offset] 转换为fp16写到cdst[dst_offset]  
}

`
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

另外，注意一点，一旦对tensor做了view或者reshape之类的操作使得内存排布不在连续，nb[i] = nb[i-1] * ne[i-1]这个条件可能就不满足了

2.1.5 Multi-Head-Attention

MHA 是整个Transformer Block中最核心的Kernel了，Attention的计算公式如下

在前文中我们也说过Llama 2 会采用一种分组共享KV cache的Attention计算GQA，但是因为我们是以7B模型为例进行说明的，7B模型并没有采用GQA，依然是采用的MHA，可参考Llama repo。所以本文还是以MHA为例进行说明此处的kernel调用情况

对于Q*K 和 Attention Score * V这两个乘法操作****，****在prompting阶段和generation阶段所调用的算子并不一样，在prompting阶段因为QKV三个都是多个单词所对应的tensor，即shape为[1, 32, seq_len , 128] ****，所以prompting阶段在处理时依然是直接调用的cublasSgemm实现。所以我们还是主要来看看generation阶段所调用的算子，在generation阶段 Q的shape为[1, 32, 1 , 128] ，Q需要与新生成的K V，以及之前推理缓存下来的KV cache一起做self-attention运算

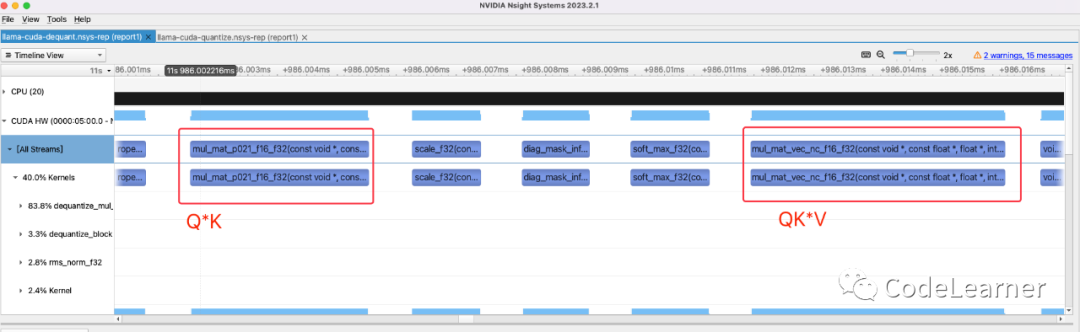
上图为generation阶段Multi-Head-Attention的算子调用，主要包括5个kernel

• Q*K 的算子——mul_mat_p021_f16_f32

generation阶段此时Q的shape是[1, 32,1,128] , K cache的shape为[1,32,seq_len,128]，此处的seq_len就是当前处理的tokens的数量，会随着generation阶段，逐渐加1。如下kernel

这里说一句，这里说的Q和K的shape只是方便理解Attention的计算过程，实际Q和K在物理内存上可能不是按shape排列的方式存储的，比如这里的K cache，内存存放的次序还是[1, seq_len, 4096]

以下kernel调用时的gridDim = {1,seq_len,32} ,blockDim = {32,1,1}，也就是说一个block处理一个头中的Q与K cache中的一行K进行乘加运算

`// gridDim = {1,seq_len,32} ,blockDim = {32,1,1}  
static __global__ void mul_mat_p021_f16_f32(  
    const void * __restrict__ vx, const float * __restrict__ y, float * __restrict__ dst,  
    const int ncols_x, const int nrows_x, const int nchannels_x, const int nchannels_y) {

    const half * x = (const half *) vx; //vx就是K cache

    const int row_x = blockDim.y*blockIdx.y + threadIdx.y; //这个维度是seq_len 的索引，[0,..,seq_len-1]  
    const int channel = blockDim.z*blockIdx.z + threadIdx.z; //这个维度是multi head的索引[0,1,2..,31]  
    const int channel_x = channel / (nchannels_y / nchannels_x);//这个是对于GQA的时候用的，就是Q分组共享K cache  
                                                                //此处我们是以7B模型为例，依然是MHA

    const int nrows_y = ncols_x;  //128  
    const int nrows_dst = nrows_x;//seq_len  
    const int row_dst = row_x; //[0,..,seq_len-1]

    float tmp = 0.0f;  
    //因为一个block(32个线程)处理128个数据，所以每个线程for循环迭代次数为128/32  
    for (int col_x0 = 0; col_x0 < ncols_x; col_x0 += blockDim.x) {  
        const int col_x = col_x0 + threadIdx.x; //计算列索引[0-127]

        if (col_x >= ncols_x) {  
            break;  
        }

        // x is transposed and permuted  
        // 计算K cache的index  
        // 前面说过K cache在内存存的次序还是[seq_len , multihead , head_dim]  
        // 所以这里的index的计算方式 理解一下  
        const int ix = row_x*nchannels_x*ncols_x + channel_x*ncols_x + col_x;  
        //K cache不是为了节省内存用的FP16存着嘛，所以用一个__half2float内置函数将FP16转换为FP32  
        const float xi = __half2float(x[ix]);  
        //K cache的列索引 等于 Q的 列索引  
        //名字叫row_y但还是列索引，因为Q的内存排布还是[32,128]  
        const int row_y = col_x;

        // y is not transposed but permuted  
        const int iy = channel*nrows_y + row_y;//计算Q的全局index

        tmp += xi * y[iy]; //乘后累和到tmp  
    }

    // dst is not transposed and not permuted  
    //dst的shape为[32,1,seq_len] ,所以内存排布为[32,seq_len]  
    //所以dst的index计算方式如下  
    const int idst = channel*nrows_dst + row_dst;

    // sum up partial sums and write back result  
    // 又是熟悉的block内求和  
#pragma unroll  
    for (int mask = 16; mask > 0; mask >>= 1) {  
        tmp += __shfl_xor_sync(0xffffffff, tmp, mask, 32);  
    }

    if (threadIdx.x == 0) {  
        dst[idst] = tmp;//写回dst  
    }  
}

`
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

• 除以 —— scale_f32

Attention(Q,K,V)公式中的Q乘K之后的除以，这个kernel没啥好说的，按元素乘

`static __global__ void scale_f32(const float * x, float * dst, const float scale, const int k) {  
    const int i = blockDim.x*blockIdx.x + threadIdx.x;

    if (i >= k) {  
        return;  
    }

    dst[i] = scale * x[i];  
}

`
1
2
3
4
5
6
7
8
9
10
11

• attention mask —— diag_mask_inf_f32

对于Attention中的mask操作，我们看下面这个图，一目了然，在原生Transformer Decode阶段，加入mask的是为了防止前面token的Q与后面token的K计算得到一个较高的Attention Score，所以通过一个上三角(且上三角元素全为-INF)矩阵，来保证句子中单词之间的时序性。

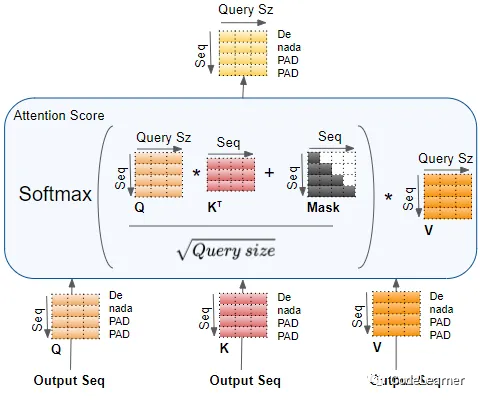
attention-mask

如下kernel就是实现mask操作的，也是逐元素，根据其坐标来判断是否需要mask。不过这里多说一句，在通过Nsight抓取的MHA部分的kernel调用情况的截图中可以看到，generation阶段也调用了diag_mask_inf_f32这个kernel，实际是不需要调用的。因为生成阶段生成的Q就是最新的单词所对应的Q，他与KV cache中的每个KV 计算的Attention Score都不会mask， mask的操作只需要存在于prompting阶段中，想来这里也是因为llama.cpp的作者为了省事～

这里不太明白为什么generation阶段不需要mask的可以移步至B站CodeLearner

`static __global__ void diag_mask_inf_f32(const float * x, float * dst, const int ncols, const int rows_per_channel, const int n_past) {  
    const int col = blockDim.x*blockIdx.x + threadIdx.x;  
    const int row = blockDim.y*blockIdx.y + threadIdx.y;

    if (col >= ncols) {  
        return;  
    }

    const int i = row*ncols + col;  
    // dst[i] = col > n_past + row ? -INFINITY : x[i];  
    dst[i] = x[i] - (col > n_past + row % rows_per_channel) * INT_MAX; // equivalent within rounding error but slightly faster on GPU  
}

`

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

• Attention Score * V 的算子 mul_mat_vec_nc_f16_f32

generation阶段Attention Score 的shape为[1, 32 , 1, seq_len]，V的shape为[1, 32 ,seq_len,128] . mul_mat_vec_nc_f16_f32算子调用的gridDim={1,128,32} ，blockDim={32,1,1} ，所以 blockDim.z维度对应于multihead=32 维度，blockDim.y维度对应于head_dim=128维度，然后每个block中32个线程用来处理每个seq_len长度序列的乘加。

`//gridDim={1,128,32},blockDim={32,1,1}  
static __global__ void mul_mat_vec_nc_f16_f32( // nc == non-contiguous  
    const void * __restrict__ vx, const float * __restrict__ y, float * __restrict__ dst, const int ncols_x, const int nrows_x,  
    const int row_stride_x, const int channel_stride_x, const int channel_x_divisor) {  
    //ncols_x = seq_len, nrows_x=128, row_stride_x=512 , channel_stride_x = 65536, channel_x_divisor=1

    const half * x = (const half *) vx; //V cache 存储时使用的FP16

    const int row_x = blockDim.y*blockIdx.y + threadIdx.y; // index of head_dim ->  0-127  
    const int channel = blockDim.z*blockIdx.z + threadIdx.z; // index of multi-head -> 0-31  
    const int channel_x = channel / channel_x_divisor; // channel/1

    const int nrows_y = ncols_x; //seq_len  
    const int nrows_dst = nrows_x; //128  
    const int row_dst = row_x; // index of head_dim ->  0-127

        //Attention Score * V 最终的shape为[1,32,1,128]  
    //所以idst = （index of multi-head） * (128) + (index of head_dim)  
    const int idst = channel*nrows_dst + row_dst; 

    float tmp = 0.0f;  
    //循环处理seq_len序列，每个线程处理seq_len/blockDim.x 个数  
    for (int col_x0 = 0; col_x0 < ncols_x; col_x0 += blockDim.x) {  
        const int col_x = col_x0 + threadIdx.x;

        if (col_x >= ncols_x) {  
            break;  
        }  
        // V cache的index  
        const int ix = channel_x*channel_stride_x + row_x*row_stride_x + col_x;  
        //fp16转fp32  
        const float xi = __half2float(x[ix]);  
        // Attention Score index  
        const int row_y = col_x;  
        const int iy = channel*nrows_y + row_y;

        tmp += xi * y[iy]; //乘加  
    }

    // sum up partial sums and write back result  
    //还是熟悉的block内部求和  
#pragma unroll  
    for (int mask = 16; mask > 0; mask >>= 1) {  
        tmp += __shfl_xor_sync(0xffffffff, tmp, mask, 32);  
    }  
    //结果写回  
    if (threadIdx.x == 0) {  
        dst[idst] = tmp;  
    }  
}

`
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

2.1.6 add_f32

add_f32 用于残差连接一下输入tensor 与Attention Block的输出，kernel的实现没啥好说的，就是最简单向量相加

`static __global__ void add_f32(const float * x, const float * y, float * dst, const int kx, const int ky) {  
    const int i = blockDim.x*blockIdx.x + threadIdx.x;

    if (i >= kx) {  
        return;  
    }  
    dst[i] = x[i] + y[i%ky];  
}

`
1
2
3
4
5
6
7
8
9
10

输入tensor shape为[1,1,4096] ,Attention Block的输出为[1,1,4096] 。在FeedForward Block最后也是同样会调用add_f32 将FeedForward Block的输入连残差连接到输出，所调用的kernel为同一个

2.2 FeedForward Block

FeedForward Block 上层算法流程以及其在prompting阶段和generation阶段所调用的CUDA算子，如下图所示。整个过程中主要的就是几个Linear层，在前面的2.1.2节中详细介绍过了，所以这里就不过多赘述了～

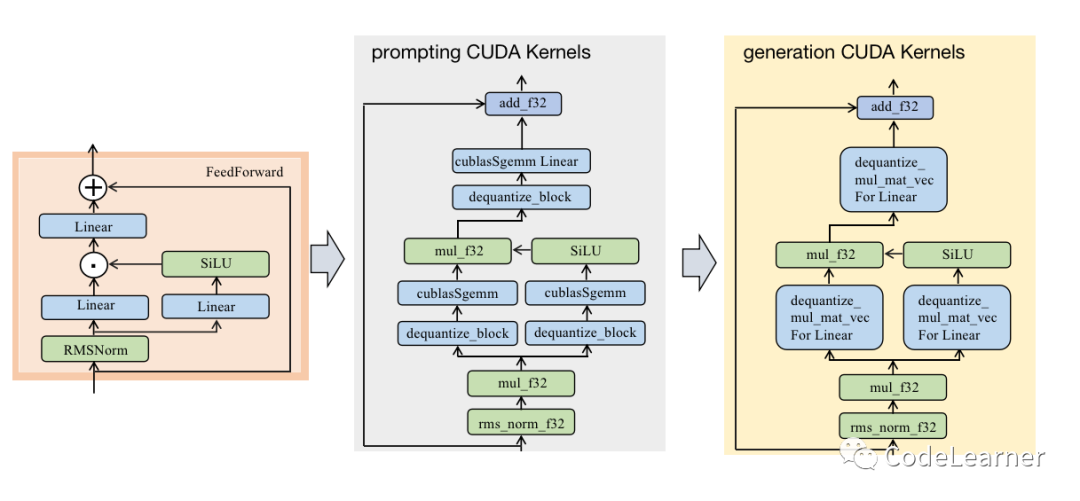
2.2.1 silu_f32

FeedForward Block中在之前没有出现过的kenrel就是silu_f32这个激活函数kernel。同样，我们先回顾一下SiLU函数的公式

`static __global__ void silu_f32(const float * x, float * dst, const int k) {  
    const int i = blockDim.x*blockIdx.x + threadIdx.x;

    if (i >= k) {  
        return;  
    }  
    //silu公式  
    dst[i] = x[i] / (1.0f + expf(-x[i]));  
}

`
1
2
3
4
5
6
7
8
9
10
11
12

整个Kernel在调用时blocksize 在prompting阶段和generation阶段的值不一样，因为FeedForward Block中前两个Linear层的输出尺寸是11008 ，所以在prompting阶段需要prompting_length * 11008 个线程来处理prompting_length * 11008 个数据，而在generation阶段则需要11008 个线程来处理11008 个数据。所以如下图所示，为generation阶段的调用silu的Nsight截图，该kernel用了43个block，每个block 256个线程，= 43 * 256。prompting阶段类比。

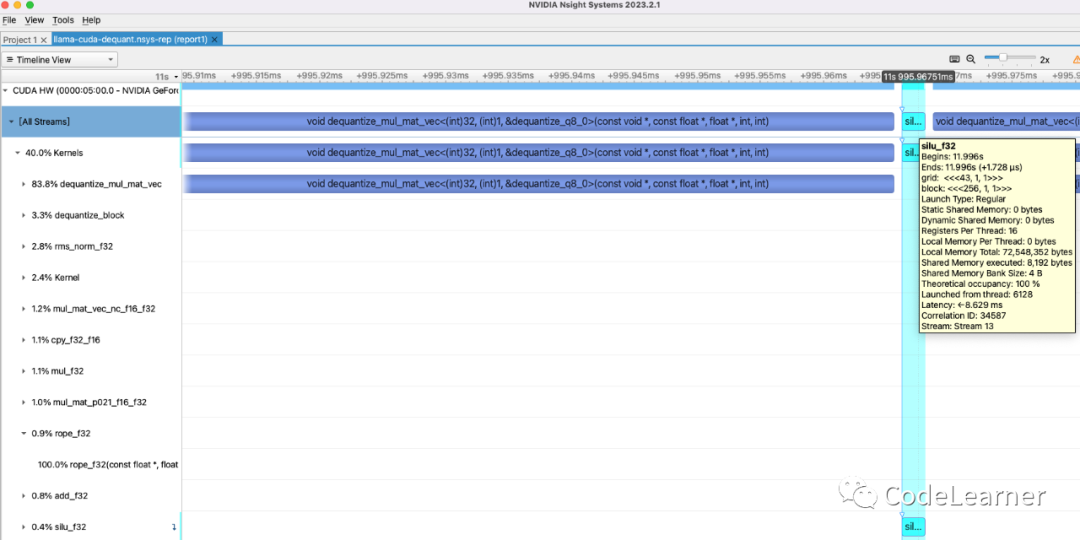
silu

至此就算把Llama 2 中完整的单个Tranformer Block中的所有llama.cpp调用的CUDA Kernel 说明完啦～