新版白话空间统计（19）空间关系对莫兰指数的影响_geoda莫兰指数散点图怎么加字

CSDN的被爬虫专用声明：虾神原创，公众号\知乎：虾神说D

转发、转载和爬虫，请主动保留此声明。

前文再续，书接上一回。

上一回我们说到用GeoDa可以自定义空间权重矩阵和空间关系，那么空间关系到底在我们的分析中，会产生什么样的影响呢？今天我们通过一个简单的例子来给大家示例一下：

首先我们用常规的方式演示一下在GeoDa里面如何做莫兰指数：

打开GeoDa，打开我们需要分析的数据，比如还是中国的人口GDP的shape file（数据获取在虾神的gitee&github上面，公众号发送 6 获取仓库地址，不会下载的，发送 仓库 二字）

点击工具条上的表格图标，可以打开查看属性表：

我们随便选择一个年份来进行距离，比如就用2016吧，可以先用2016年的各省GDP来做一个分位数地图渲染：

在地图窗口上点击鼠标右键，然后选择“更改当前地图类型”——“分位数”——5，把地图分成五级：

然后选定要渲染的字段，比如这里选的GDP2016：

就可以看见根据GDP，对全国的数据分成了5个等级：

GeoDa做探索性数据分析的功能极强，效果也非常好，大家可以自行探索，依然保持了它的一贯特色：简明扼要，简单好用。

下面就可以做空间关系了，具体流程不解释了，大家可以回去看上一篇文章：

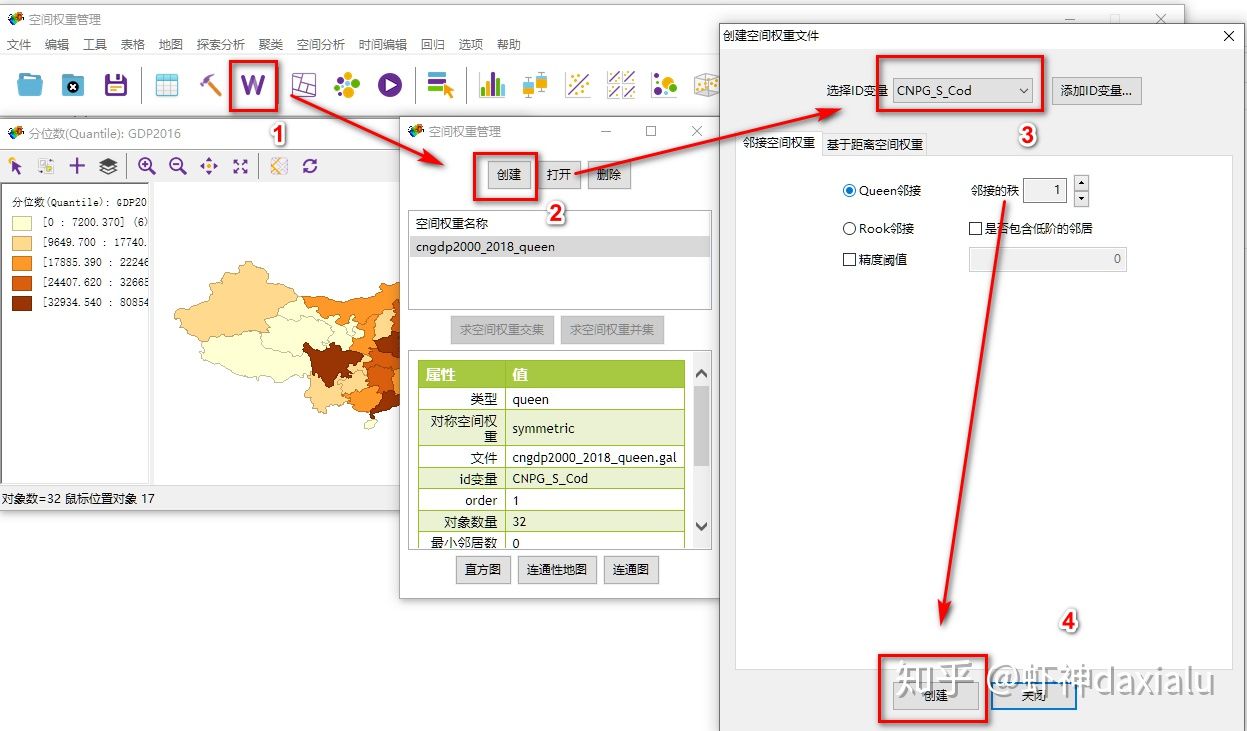
创建完成之后，直接点击空间分析——单变量Moran's I：

选定要分析的字段，点击确定，就完成了计算：

当然， 这里肯定会爆出一个警告，有独立要素，系统告诉你，它们就不参与计算了，这种情况你当然只能选是：

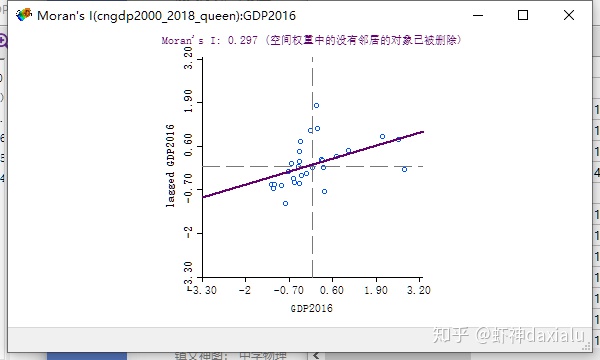
结果如下：最上面的要的title，就是我们要的结果：Moran's I : 0.297，下面是莫兰指数的散点图，关于这个散点图的原理和作用，我们以后将LISA的时候，会给大家详细解答：

记住这个数值，下面我们修改一下空间关系，比如我用中国传统六大区域法来组织空间关系：

空间关系矩阵定义如下：（截图了一部分，其他到仓库里面去看原数据）

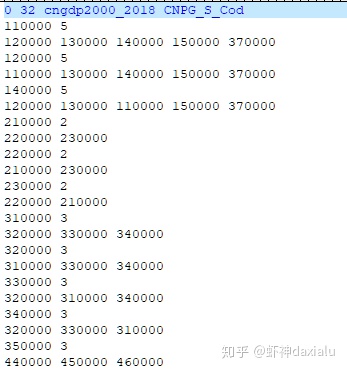
然后导入到GeoDa里面，查看连接图：

结果如下：

可以看见，我们按照传统中国7大区划，划分了区域，然后再做一个Moran's I，这一次空间权重矩阵，选择七大区域这个：

得到了一个不一样的结果：在传统的七大区域定义模式下的，Moran's I为0.126。

可以看见，同一份数据，在不同的空间关系下，显示出了不同的结论，从0.297直接降到了0.126，P值直接超过0.13，降幅几近60%，基本上就等于从高度聚集变成了随机分布……

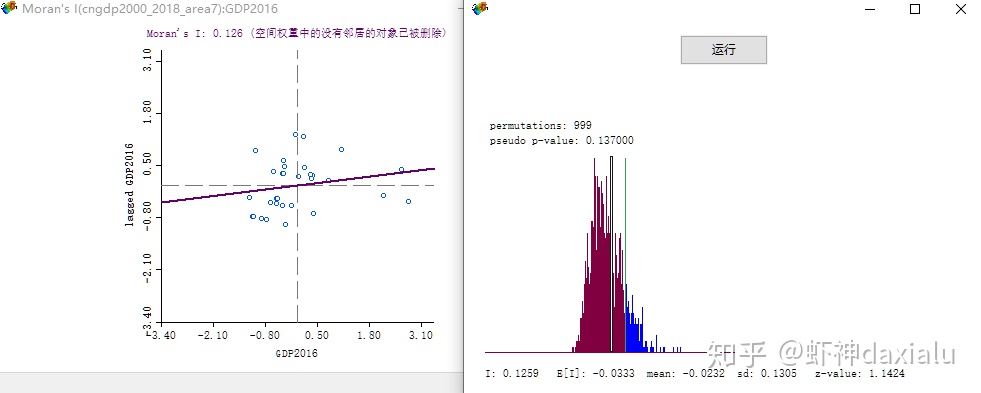
到这里，可能就有同学就会问了，莫兰指数下降代表什么呢？前面我们说过了，正向的莫兰指数代表了数据表现出了正相关的聚集模式。也就是所谓的“强的旁边，普遍出现强省；弱的旁边普遍出现弱的”。

那么我们可以就上面的实验解读如下：

1、在自然相邻的关系，空间分布呈现的正相关趋势更高，说明了在经济发展下，自然相邻的省域经济关联程度更高。相较之下，如果按照七大区域的划分方法，经济的关联程度会有所降低，但是发展均衡程度要比自然相邻方式要高。

用大白话来解释一下：

如果我们给定一个比较极端的情况，只允许空间关系规定的，相邻的省份之间进行经济活动，（自然相邻的省份与接壤的省，七大区域与自身区域内的省进行相关经济活动，那么自然相邻的省份要比区域封闭的省相关性更高。

正相关和聚集，除了可以表现为强强聚集，发展不均衡以外，还可以代表领头羊带动作用，跟着强省在一起，自身也会变得强一些，反之亦然（近朱者赤近墨者黑）。那么极端情况下，如果就按七大区域划分，不与其他区域交流的话，强省对弱省的带动，要弱于自然相邻情况下。

也可以视为，七大区域分区的方法，会让每个区域内出现强省和弱省的概率都相等，而强省对弱省的带动效应并不十分明显。

我们可以用两种空间模式，做一个2000年-2018年，18年的比较，当然，如果你用GeoDa工具一个个做，也是阔以的……也就是18 * 2 = 36次而已，一般来说，能够选择编程实现，就不用做这种劳力活了，能够读取GeoDa空间权重矩阵的方式有很多，比如R语言的spdep包，或者Python的PySAL，都可以，我们选择最简单的一种，R语言来实现，编写脚本如下：

分析结果如下：

需要源代码以及数据的，在公众号发送“R语言”，获得仓库地址。

打完收工。

CSDN的被爬虫专用声明：虾神原创，公众号\知乎：虾神说D

转发、转载和爬虫，请主动保留此声明。