统计学中，似然函数是一种关于统计模型参数的函数，表示模型参数中的似然性。计算上：给定输出x时，关于参数θ的似然函数L(θ|x)（在数值上）等于给定参数θ后数据X的概率：L(θ|x)=P(X=x|θ)。简单意思就是，把参数设出来，记为θ，那似然函数就是在参数θ下，样本事件所发生的概率表述。但是我们要注意在统计学中，似然和概率又不一样，概率用于在已知一些参数的情况下，预测接下来的观测所得到的结果，而似然性则是用于在已知某些观测所得到的结果时，对有关事物的性质的参数进行估计。

1.2先验概率p(θ)

先验概率（prior probability）通俗来讲是指根据以往经验和分析得到的概率分布。

1.3后验概率P(θ|x)

在贝叶斯统计中，一个随机事件或者一个不确定事件的后验概率是在给出相关证据或数据后所得到的条件概率。

1.4共轭先验分布

共轭，顾名思义，两个及以上的对象，互相牵制、控制。

那在贝叶斯理论里，在已知似然函数情况下（已经有样本数据了），根据先验概率函数求后验概率。问题是：选取什么样的先验分布，会让后验分布与先验分布具有相同的数学形式呢，从这里提出了共轭分布理论。

在贝叶斯概率理论中，如果后验概率P(θ|x)和先验概率p(θ)满足同样的分布律（同分布），那么，先验分布叫作似然函数的共轭先验分布，先验分布和后验分布被叫作共轭分布。

共轭先验的好处主要在于代数上的方便性，可以直接给出后验分布的封闭形式，否则的话只能数值计算。共轭先验也有助于获得关于似然函数如何更新先验分布的直观印象。

2.pLSA

本章节出处：https://blog.csdn.net/xiaocong1990/article/details/72662052

主题模型就是用来对文档建模的数学工具，它是一个生成模型，何谓生成模型，就是要求的目标概率，必须先通过求联合概率，然后再利用概率运算公式得到。一般符合下式：

其中， P(y|x) 是要求的结果，表示给定输入量，输出关于输入的概率分布。

从上式中可以明显看到生成模型的结果并不是直接从数据中得到的，它有一个中间过程。

在主题模型的框架里，每一篇文档的产生都遵循着这样一个步骤：每一篇文档都有一系列主题，这些主题共同符合一定的概率分布（当然不同文档的主题概率分布不尽相同），依据这个概率分布随机选择一个主题，然后再从这个主题里按照另一个概率分布选择一个词。这个词就是文档的第一个词，其余的词都是这个过程。用公式来表示就是：

P(词|文档)= $\sum$ P(词|主题)P(主题|文档)

矩阵表示为：

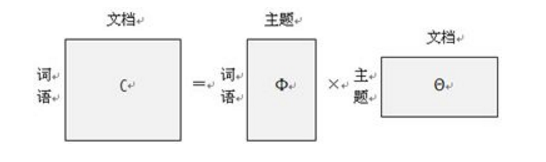
主题模型有很多方法，主要有两种：pLSA(Probabilistic latent semantic analysis)和LDA(Latent Dirichlet allocation)。

pLSA的另一个名称是probabilistic latent semantic indexing(pLSI)，假设在一篇文档d中，主题用c来表示，词用w来表示，则有如下公式：

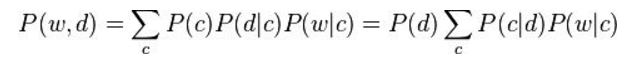
第一个等式是对称形式，其主要思路是认为文档和词都按照一定的概率分布（分别是P(d|c)和P(w|c)）从主题c中产生；第二个等式是非对称形式，更符合我们的直觉，主要思路是从该文档中按照一定概率分布选择一个主题（即P(c|d)），然后再从该主题中选择这个词，这个概率对应是P(w|c)，这个公式恰好和上文所讲的一致。即把这里的非对称形式的公式左右都除以P(d)便得到下面这个公式：

即有M篇文档，每一篇文档d自身有个概率P(d)，从d到主题c有一个概率分布P(c|d)，随后从主题c到词w又是一个概率分布P(w|c)，由此构成了w和c的联合概率分布P(w,d)。

pLSA的参数个数是cd+wc，

所以参数个数随着文档d的增加而线性增加。但是很重要的的是，pLSA只是对已有文档的建模，也就是说生成模型只是适合于这些用以训练pLSA算法的文档，并不是新文档的生成模型。这一点很重要，因为我们后文要说的pLSA很容易过拟合，还有LDA为了解决这些问题引入的狄利克雷分布都与此有关。

3.LDA（Latent Dirichlet allocation）

本段参考来源：

作者：weizier
链接：https://www.zhihu.com/question/23642556/answer/38969800
来源：知乎

在LDA中，每一篇文档都被看做是有一系列主题，在这一点上和pLSA是一致的。实际上，LDA的不同之处在于，pLSA的主题的概率分布P(c|d)是一个确定的概率分布，也就是虽然主题c不确定，但是c符合的概率分布是确定的，比如符合高斯分布，这个高斯分布的各参数是确定的，但是在LDA中，这个高斯分布都是不确定的，高斯分布又服从一个狄利克雷先验分布(Dirichlet prior)，说的绕口一点是主题的概率分布的概率分布，除了主题有这个特点之外，另外词在主题下的分布也不再是确定分布，同样也服从一个狄利克雷先验分布。所以实际上LDA是pLSA的改进版，延伸版。

这个改进有什么好处呢？就是我们上文说的pLSA容易过拟合，何谓过拟合？过拟合就是训练出来的模型对训练数据有很好的表征能力，但是一应用到新的训练数据上就挂了。这就是所谓的泛化能力不够。我们说一个人适应新环境的能力不行，也可以说他在他熟悉的环境里过拟合了。

那为什么pLSA容易过拟合，而LDA就这么牛逼呢？这个要展开讲，可以讲好多好多啊，可以扯到频率学派和贝叶斯学派关于概率的争论，这个争论至今悬而未决，在这里，我讲一下我自己的看法，说的不对的，希望指正。

pLSA中，主题的概率分布P(c|d)和词在主题下的概率分布P(w|c)既然是概率分布，那么就必须要有样本进行统计才能得到这些概率分布。更具体的讲，主题模型就是为了做这个事情的，训练已获得的数据样本，得到这些参数，那么一个pLSA模型便得到了，但是这个时候问题就来了：这些参数是建立在训练样本上得到的。这是个大问题啊！你怎么能确保新加入的数据同样符合这些参数呢？你能不能别这么草率鲁莽？但是频率学派就有这么任性，他们认为参数是存在并且是确定的，只是我们未知而已，并且正是因为未知，我们才去训练pLSA的，训练之后得到的参数同样适合于新加入的数据，因为他们相信参数是确定的，既然适合于训练数据，那么也同样适合于新加入的数据了。

但是真实情况却不是这样，尤其是训练样本量比较少的情况下的时候，这个时候首先就不符合大数定律的条件（这里插一句大数定律和中心极限定律，在无数次独立同分布的随机事件中，事件的频率趋于一个稳定的概率值，这是大数定律；而同样的无数次独立同分布的随机事件中，事件的分布趋近于一个稳定的正态分布，而这个正太分布的期望值正是大数定律里面的概率值。所以，中心极限定理比大数定律揭示的现象更深刻，同时成立的条件当然也要相对来说苛刻一些。非数学系出身，不对请直接喷），所以频率并不能很好的近似于概率，所以得到的参数肯定不好。我们都知道，概率的获取必须以拥有大量可重复性实验为前提，但是这里的主题模型训练显然并不能在每个场景下都有大量的训练数据。所以，当训练数据量偏小的时候，pLSA就无可避免的陷入了过拟合的泥潭里了。为了解决这个问题，LDA给这些参数都加入了一个先验知识，就是当数据量小的时候，我人为的给你一些专家性的指导，你这个参数应该这样不应该那样。比如你要统计一个地区的人口年龄分布，假如你手上有的训练数据是一所大学的人口数据，统计出来的结果肯定是年轻人占比绝大多数，这个时候你训练出来的模型肯定是有问题的，但是我现在加入一些先验知识进去，专家认为这个地区中老年人口怎么占比这么少？不行，我得给你修正修正，这个时候得到的结果就会好很多。所以LDA相比pLSA就优在这里，它对这些参数加入了一些先验的分布进去。（但是我这里并没有任何意思说贝叶斯学派优于频率学派，两学派各有自己的优势领域，比如很多频率学派对贝叶斯学派的攻击点之一是，在模型建立过程中，贝叶斯学派加入的先验知识难免主观片面，并且很多时候加入都只是为了数学模型上运算的方便。我这里只是举了一个适合贝叶斯学派的例子而已）

但是，当训练样本量足够大，pLSA的效果是可以等同于LDA的，因为过拟合的原因就是训练数据量太少，当把数据量提上去之后，过拟合现象会有明显的改观。

4.LDA数学分析

本章节参考出处：https://www.cnblogs.com/pinard/p/6831308.html

LDA是基于贝叶斯模型的，涉及到贝叶斯模型离不开“先验分布”，“数据（似然）”和"后验分布"三块。在朴素贝叶斯算法原理小结中我们也已经讲到了这套贝叶斯理论。在贝叶斯学派这里：

先验分布 + 数据（似然）= 后验分布

　　　　这点其实很好理解，因为这符合我们人的思维方式，比如你对好人和坏人的认知，先验分布为：100个好人和100个的坏人，即你认为好人坏人各占一半，现在你被2个好人（数据）帮助了和1个坏人骗了，于是你得到了新的后验分布为：102个好人和101个的坏人。现在你的后验分布里面认为好人比坏人多了。这个后验分布接着又变成你的新的先验分布，当你被1个好人（数据）帮助了和3个坏人（数据）骗了后，你又更新了你的后验分布为：103个好人和104个的坏人。依次继续更新下去。

LDA主题模型

问题是这样的，我们有MM篇文档，对应第d个文档中有有NdNd个词。即输入为如下图：

我们的目标是找到每一篇文档的主题分布和每一个主题中词的分布。在LDA模型中，我们需要先假定一个主题数目KK，这样所有的分布就都基于KK个主题展开。那么具体LDA模型是怎么样的呢？具体如下图：

LDA假设文档主题的先验分布是Dirichlet分布，即对于任一文档dd, 其主题分布θdθd为：

其中，αα为分布的超参数，是一个KK维向量。

LDA假设主题中词的先验分布是Dirichlet分布，即对于任一主题kk, 其词分布βkβk为：

其中，ηη为分布的超参数，是一个VV维向量。VV代表词汇表里所有词的个数。

对于数据中任一一篇文档dd中的第nn个词，我们可以从主题分布θdθd中得到它的主题编号zdnzdn的分布为：

而对于该主题编号，得到我们看到的词wdnwdn的概率分布为：

理解LDA主题模型的主要任务就是理解上面的这个模型。这个模型里，我们有MM个文档主题的Dirichlet分布，而对应的数据有MM个主题编号的多项分布，这样(α→θd→z⃗ dα→θd→z→d)就组成了Dirichlet-multi共轭，可以使用前面提到的贝叶斯推断的方法得到基于Dirichlet分布的文档主题后验分布。

如果在第d个文档中，第k个主题的词的个数为：n(k)dnd(k), 则对应的多项分布的计数可以表示为：

利用Dirichlet-multi共轭，得到θdθd的后验分布为：

同样的道理，对于主题与词的分布，我们有KK个主题与词的Dirichlet分布，而对应的数据有KK个主题编号的多项分布，这样(η→βk→w(k))就组成了Dirichlet-multi共轭，可以使用前面提到的贝叶斯推断的方法得到基于Dirichlet分布的主题词的后验分布。如果在第k个主题中，第v个词的个数为：n(v)knk(v), 则对应的多项分布的计数可以表示为：

利用Dirichlet-multi共轭，得到βkβk的后验分布为：

由于主题产生词不依赖具体某一个文档，因此文档主题分布和主题词分布是独立的。理解了上面这M+KM+K组Dirichlet-multi共轭，就理解了LDA的基本原理了。

现在的问题是，基于这个LDA模型如何求解我们想要的每一篇文档的主题分布和每一个主题中词的分布呢？

一般有两种方法，第一种是基于Gibbs采样算法求解，第二种是基于变分推断EM算法求解。

5.LDA的应用场景和缺点

应用场景一般有四种：

(1) 相似文档发现。(2) 新闻个性化推荐。(3) 自动打标签。(4) wordRank

缺点：处理短文本效果不太理想。

6.LDA的sklearn实现及其参数

本章节参考出处：https://www.cnblogs.com/pinard/p/6908150.html

在scikit-learn中,LDA主题模型的类在sklearn.decomposition.LatentDirichletAllocation包中，其算法实现主要基于变分推断EM算法，而没有使用基于Gibbs采样的MCMC算法实现。

scikit-learn除了我们标准的变分推断EM算法外，还实现了另一种在线变分推断EM算法，它在原理篇里的变分推断EM算法的基础上，为了避免文档内容太多太大而超过内存大小，而提供了分步训练(partial_fit函数)，即一次训练一小批样本文档，逐步更新模型，最终得到所有文档LDA模型的方法。

scikit-learn LDA主题模型主要参数和方法

我们来看看LatentDirichletAllocation类的主要输入参数:

　　　　1) n_topics: 即我们的隐含主题数KK,需要调参。KK的大小取决于我们对主题划分的需求，比如我们只需要类似区分是动物，植物，还是非生物这样的粗粒度需求，那么KK值可以取的很小，个位数即可。如果我们的目标是类似区分不同的动物以及不同的植物，不同的非生物这样的细粒度需求，则KK值需要取的很大，比如上千上万。此时要求我们的训练文档数量要非常的多。

　　　　2) doc_topic_prior:即我们的文档主题先验Dirichlet分布θdθd的参数αα。一般如果我们没有主题分布的先验知识，可以使用默认值1/K1/K。

　　　　3) topic_word_prior:即我们的主题词先验Dirichlet分布βkβk的参数ηη。一般如果我们没有主题分布的先验知识，可以使用默认值1/K1/K。

　　　　4) learning_method: 即LDA的求解算法。有 ‘batch’ 和 ‘online’两种选择。 ‘batch’即我们在原理篇讲的变分推断EM算法，而"online"即在线变分推断EM算法，在"batch"的基础上引入了分步训练，将训练样本分批，逐步一批批的用样本更新主题词分布的算法。默认是"online"。选择了‘online’则我们可以在训练时使用partial_fit函数分布训练。不过在scikit-learn 0.20版本中默认算法会改回到"batch"。建议样本量不大只是用来学习的话用"batch"比较好，这样可以少很多参数要调。而样本太多太大的话，"online"则是首先了。

　　　　5）learning_decay：仅仅在算法使用"online"时有意义，取值最好在(0.5, 1.0]，以保证"online"算法渐进的收敛。主要控制"online"算法的学习率，默认是0.7。一般不用修改这个参数。

　　　　6）learning_offset：仅仅在算法使用"online"时有意义，取值要大于1。用来减小前面训练样本批次对最终模型的影响。

　　　　7） max_iter ：EM算法的最大迭代次数。

　　　　8）total_samples：仅仅在算法使用"online"时有意义，即分步训练时每一批文档样本的数量。在使用partial_fit函数时需要。

　　　　9）batch_size: 仅仅在算法使用"online"时有意义，即每次EM算法迭代时使用的文档样本的数量。

　　　　10）mean_change_tol :即E步更新变分参数的阈值，所有变分参数更新小于阈值则E步结束，转入M步。一般不用修改默认值。

　　　　11） max_doc_update_iter: 即E步更新变分参数的最大迭代次数，如果E步迭代次数达到阈值，则转入M步。

　　　　从上面可以看出，如果learning_method使用"batch"算法，则需要注意的参数较少，则如果使用"online",则需要注意"learning_decay", "learning_offset"，“total_samples”和“batch_size”等参数。无论是"batch"还是"online", n_topics(KK), doc_topic_prior(αα), topic_word_prior(ηη)都要注意。如果没有先验知识，则主要关注与主题数KK。可以说，主题数KK是LDA主题模型最重要的超参数。

6.scikit-learn LDA中文主题模型实例


from sklearn.feature_extraction.text import CountVectorizer
from sklearn.decomposition import LatentDirichletAllocation
 
corpus = [] # corpus为语料，包含多个sentence
 
cntVector = CountVectorizer(stop_words='stopwordslist') # stopwordslist为停用词list
 
cntTf = cntVector.fit_transform(corpus) # 转换词频向量
 
print (cntTf)
# 定义LDA模型 
lda = LatentDirichletAllocation(n_topics=2,
                                learning_offset=50.,
                                random_state=0)
 
docres = lda.fit_transform(cntTf)
 
print (docres) # 主题分部
print (lda.components_) # 主题词分布

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/Gausst松鼠会/article/detail/289939