python基于预训练大模型权重实现文本向量化开发构建微博评论数据情感极向识别模型_python 大模型

因为最近的一些项目涉及到了大模型相关的技术开发研究，在我前面的博文中也已经有一些实践记录学习资料分享的文章了，今天是在做模型训练的时候突然想到一个有意思的想法，按照我之前做文本分类的方法，基本主流的技术路线都是先对文本数据进行清洗分词处理，之后借助于指定的算法开发实现文本向量化处理，最终搭建机器学习模型或者是深度学习模型来实现文本数据的分类处理，这里其实比较重要的一部分就是文本向量化的实现。

下面是一个文本分类的详细实现流程：

1. 数据准备：首先，需要准备好用于训练和评估的文本数据集。这可以是一个已经标注好类别的数据集，其中每个样本都有一个对应的类别标签。

2. 数据预处理：对文本数据进行预处理，包括清洗、分词、去除停用词等操作。可以使用常见的Python库如nltk或中文分词工具例如jieba来执行这些步骤。

3. 特征提取：将文本转换成机器学习算法可以处理的特征表示。常用的方法包括使用词袋模型（Bag-of-Words）、TF-IDF、Word2Vec、BERT等。选择适合任务需求的特征提取方法。

4. 划分数据集：将数据集划分为训练集和测试集。训练集用于构建分类模型，测试集用于评估模型性能。

5. 模型选择与训练：选择适合文本分类的模型，例如朴素贝叶斯、支持向量机、深度学习模型如卷积神经网络（CNN）、循环神经网络（RNN）或Transformer-based模型（如BERT）。使用训练集上的数据对模型进行训练。

6. 模型评估：使用测试集上的数据对训练好的模型进行评估。常用的评估指标包括准确率、精确率、召回率、F1值等。

7. 调参与优化：根据评估结果，进行模型的调参与优化。可以尝试不同的超参数配置、特征提取方法或模型架构。

8. 模型应用：使用训练好的模型对新的未标记文本进行分类预测。

以上是一个通用的文本分类实现流程，具体的步骤和代码实现会根据选定的算法和工具库而有所不同。在每个步骤中，根据任务需求和数据特点进行调整，并进行适当的实验和改进来提高模型的性能。

最近受到一些chatGPT类模型的启发，我就想如果不自己开发训练词向量化模型直接使用这些预训练开源的模型权重怎么样，是否是可行的呢？

本文的核心目的就是想要实现验证这一流程，这里选用的是之前制作的微博情感极向数据集，为了简单期间，我这里仅仅是分成了正向情感和负向情感，每个类别的数据集都只选取了1000条的样本数据，因为数据量越多计算时间也越久，这里我主要是以实践为主。

首先来简单看下数据集：
正向情感数据截图如下所示：

 负向情感数据如下所示：

 接下来我们来看基于预训练大模型权重开发实现文本向量化的方法，其实借助于现成的transformer库可以说是非常非常简单化了，如下所示：

from transformers import TFBertTokenizer
 
tokenizer= TFBertTokenizer.from_pretrained("这里填入你选择的模型即可")

接下来就可以实现文本的向量化了，核心代码实现如下所示：

# 将文本序列转换为模型输入张量
inputs = tokenizer.convert_ids_to_tensors(tokens)
 
# 获取文本的向量表示
outputs = model(**inputs)
text_vector = outputs.pooler_output
 
# 打印文本向量
print(text_vector)

接下来只需要自己简单的编写一个循环处理转化的语句即可实现数据集整体批量的转化处理了，这里就不再赘述了。

完成文本的向量化处理之后接下来就是可以搭建模型实现文本数据的分类处理了，这里我选用的是机器学习里面比较有特色的三种模型，分别是：逻辑回归模型、支持向量机模型和随机森林模型。

逻辑回归模型：

逻辑回归（Logistic Regression）是一种用于二分类问题的机器学习算法。尽管名字中带有"回归"，但实际上它是一种分类算法。

在逻辑回归中，我们试图建立一个能够根据输入特征预测样本属于某一类别的概率的模型。逻辑回归通过将线性函数的输出映射到一个[0,1]之间的值，并使用一个阈值来判定样本属于哪个类别。

下面是逻辑回归模型的数学表示：

给定一个样本的输入特征向量为 x，逻辑回归模型通过以下公式计算样本属于正类的概率 P(y=1|x)：

[ P(y=1|x) = \frac{1}{1 + e^{-z}} ]

其中，z 是一个线性函数：

[ z = b + w_1x_1 + w_2x_2 + \ldots + w_nx_n ]

b 是偏置项（intercept），w 是权重矩阵，x 是输入特征向量。

训练逻辑回归模型主要涉及以下几个步骤：

1. 数据准备：收集并整理包含特征和对应类别标签的训练数据集。

2. 特征缩放：对输入特征进行缩放，以确保它们的值范围在合理的区间内，避免梯度下降等优化算法受到不必要的影响。

3. 参数初始化：初始化模型的权重和偏置项。

4. 定义损失函数：选择适当的损失函数来衡量模型的预测值与真实标签之间的差异。在逻辑回归中，常用的损失函数是二元交叉熵损失函数。

5. 优化算法：使用优化算法（如梯度下降）来最小化损失函数，并更新模型的参数。

6. 模型评估：使用测试集对训练好的模型进行评估，计算分类准确率、精确率、召回率等指标。

逻辑回归模型具有以下优点：

• 实现简单，计算效率高。
• 可解释性强，可以理解各个特征对结果的贡献程度。
• 对于线性可分的数据，逻辑回归能够表现良好。

然而，逻辑回归也有一些限制：

• 逻辑回归是一个线性分类模型，对于非线性问题表现较差。
• 对异常值敏感，可能会导致模型的性能下降。
• 无法处理类别不平衡的数据集。

尽管逻辑回归在某些情况下可能不够灵活，但其简单性和可解释性使其成为许多分类问题的有用工具。

代码实现实现如下所示：

model = LogisticRegression()
model.fit(X_train, y_train)
y_predict = model.predict(X_test)
y_pred = y_predict.tolist()
accuracy = model.score(X_test, y_test)
print("LogisticRegression model accuracy: ", accuracy)

支持向量机模型：

支持向量机（Support Vector Machine，SVM）是一种常用的监督学习算法，用于二分类和多分类问题。它的目标是找到一个超平面，将不同类别的样本尽可能地分开，并最大化样本与超平面之间的间隔。

以下是支持向量机模型的详细解释：

1. 线性可分情况：在线性可分的情况下，SVM试图找到一个最优的超平面，将两个不同类别的样本分开。这个超平面被定义为具有最大间隔的那个，即离两个类别最近的样本点的距离最大化。

2. 非线性可分情况：如果数据不是线性可分的，SVM可以通过使用核函数来引入非线性映射，将数据从原始特征空间映射到一个高维特征空间。在高维特征空间中，数据可能变得线性可分。常用的核函数有线性核、多项式核和高斯核等。

3. 支持向量：在训练过程中，SVM选择了一些样本作为“支持向量”，这些样本位于超平面附近或对分类超平面有较大影响。支持向量决定了超平面的位置和边界。

4. 优化问题：支持向量机的训练过程可以转化为一个凸优化问题，通过最小化正则化的损失函数来求解。其中损失函数通常是Hinge损失或对率损失。

5. 软间隔与正则化：在实际应用中，数据很少是完全线性可分的，SVM引入了“软间隔”概念，允许一些样本位于超平面的错误一侧。通过设置惩罚参数C，可以控制分类错误与间隔之间的权衡关系。较大的C值会增强对错误分类的惩罚，可能导致更复杂的模型。

6. 多类别分类：SVM也可以用于解决多类别分类问题。一种常见的方法是使用一对多（One-vs-Rest）策略，将每个类别与其余类别进行二分类比较。

SVM具有以下优点：

• 在高维空间中表现良好，适用于处理高维数据。
• 可以通过核函数处理非线性问题。
• 泛化能力强，对于少量支持向量的改变不敏感。
• 通过调整惩罚参数C可以控制模型的复杂度和鲁棒性。

然而，SVM也有一些限制：

• 当数据集非常大时，训练时间可能很长。
• 对于多类别分类问题，需要进行额外的处理。
• 需要选择合适的核函数和调整超参数。

支持向量机是一种强大的算法，在各种任务中被广泛应用。选择适当的核函数和调整参数，可以发挥它的优势并取得良好的分类效果。

核心代码实现如下所示：

model = SVC(
            kernel="linear",
            C=10,
            gamma="auto",
            degree=5,
            tol=0.1,
            decision_function_shape="ovo",
        )
model.fit(X_train, y_train)
y_predict = model.predict(X_test)
y_pred = y_predict.tolist()
accuracy = model.score(X_test, y_test)
print("SVM model accuracy: ", accuracy)

随机森林模型：

随机森林（Random Forest）是一种集成学习方法，用于解决分类和回归问题。它通过组合多个决策树来进行预测，并结合这些决策树的结果来做出最终的预测。

以下是随机森林模型的详细解释：

1. 决策树：决策树是由节点和边组成的树状结构，用于对数据进行分类和回归。每个节点表示一个特征，每个边代表一个特征值。从根节点开始，根据特征对样本进行划分，直到达到叶节点并得到一个预测结果。

2. 随机森林的组成：随机森林由多个决策树组成，每个决策树使用不同的训练样本和特征子集进行训练。这种随机性可以增加模型的多样性，并减少过拟合风险。最终的预测结果由所有决策树的投票或平均值决定。

3. 特征选择：在每个决策树的训练过程中，随机森林会随机选择特征的子集作为候选的划分特征。这种随机选择有助于避免某些特征对整体模型的过度依赖。

4. 决策树生长：每个决策树通常通过递归地进行二分划分来生长。随机森林可以设置树的最大深度、叶节点最小样本数等参数来控制决策树的复杂度。

5. 预测和集成：对于分类问题，随机森林采用多数投票的方式得出最终的预测结果；对于回归问题，随机森林将各个决策树的预测结果取平均值作为最终的预测结果。

6. 优点：

   • 随机森林在处理高维数据和大规模数据时表现较好。
   • 它能够处理缺失值和不平衡数据。
   • 对异常值有一定的鲁棒性。

7. 限制：

   • 随机森林可能会在某些噪声较大的数据集上产生过拟合。
   • 训练时间相对较长，特别是当决策树数量较多时。

随机森林是一种强大且广泛使用的机器学习算法，适用于许多分类和回归问题。通过调整参数，如决策树数量和特征子集大小等，可以优化随机森林模型的性能。

核心代码实现如下所示：

model = RandomForestClassifier(n_estimators=200)
model.fit(X_train, y_train)
y_predict = model.predict(X_test)
y_pred = y_predict.tolist()
accuracy = model.score(X_test, y_test)
print("RandomForestClassifier model accuracy: ", accuracy)

我们依次训练开发构建了三种不同的模型，并对模型的性能进行了评估分析，结果详情如下所示：

{
	"svm": {
		"accuracy": 0.856,
		"F_value": 0.8559792610135859,
		"precision": 0.8559587813620072,
		"recall": 0.8560271429485948
	},
	"lr": {
		"accuracy": 0.884,
		"F_value": 0.8839981439703035,
		"precision": 0.8840885816692268,
		"recall": 0.8841623455604635
	},
	"rf": {
		"accuracy": 0.948,
		"F_value": 0.9479966717869943,
		"precision": 0.948715484656288,
		"recall": 0.9483707829204277
	}
}

为了直观进行对比分析可视化，这里绘制对比柱状图，如下所示：

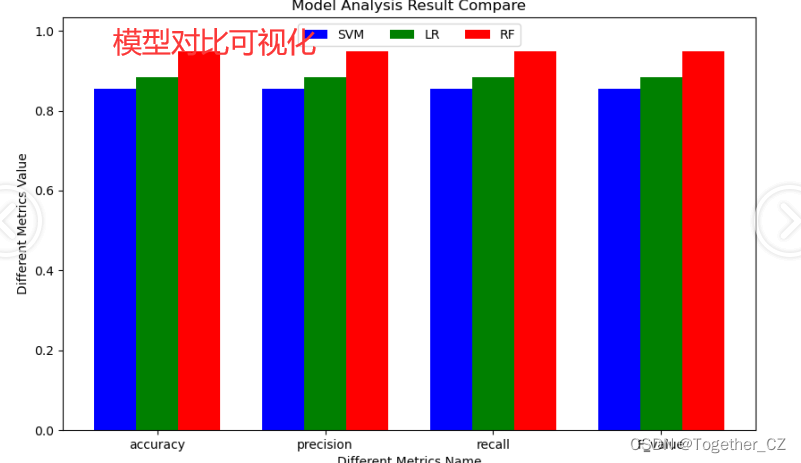
 接下来我们想要更加深入细致的分析不同子类别下模型的性能是否会有显著的差异，这里依次对三款不同的模型依次进行单独子类别的计算测试分析，结果如下所示：

【逻辑回归模型】

 【随机森林模型】

 【支持向量机模型】

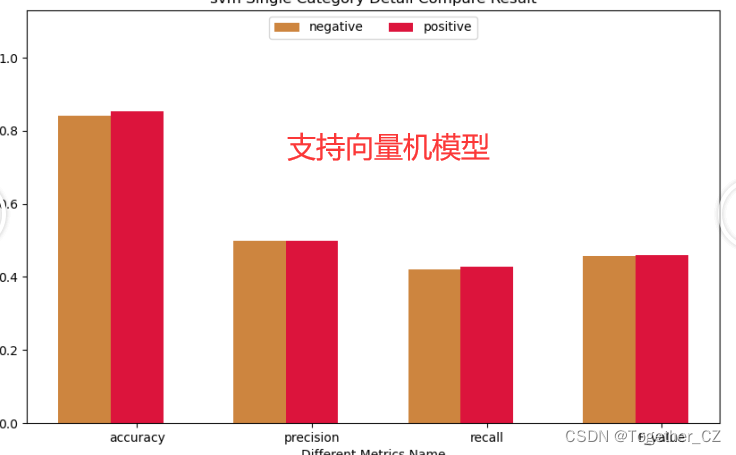
 从整体实验结果分析对比来看：随机森林的模型效果最优，另外针对不同子类别数据来说，三款模型呈现出来的整体趋势基本一致，并没有出现很明显的差异化或者是在不同子类别上有明显的差异，还是比较不错的。感兴趣的话都可以试试。