文本生成（二）【NLP论文复现】Relative position representations 相对位置编码突破Bert的文本长度限制！_相对位置编码bert

---

前言

论文原文：
Self-Attention with Relative Position Representations
NEZHA: NEURAL CONTEXTUALIZED REPRESENTATION FOR CHINESE LANGUAGE UNDERSTANDING

最近在研究苏神的《SPACES：“抽取-生成”式长文本摘要（法研杯总结）》
面向法律领域裁判文书的长文本摘要生成，涉及到长文的输入与输出，其输入加输出长度远超过bert限定的512，（Bert的postion_embedding是在预训练过程中训练好的，最长为512)。因此需要寻找解决突破输入长度限制的方法，目前了解到的解决方案：

1. Bert层次编码
2. T5模型相对位置编码
3. NEZHA相对位置编码

本文选择了华为的NEZHA模型的相对位置编码作为复现目标，先比T5来说，NEZHA沿用了 Self-attention with relative position representations 文中的相对位置编码方法，实现起来较为简单，并不需要给模型增加额外的可训练参数，问题在于增加了模型的计算量。

---

Self-Attention with Relative Position Representations

1. position_embedding的意义：position_embedding表征了token在输入中的位置信息，该位置信息主要在self-attention阶段被利用，具体可以理解为，在self-attention阶段，我们希望attention不仅要考虑word-embedding的信息，同时也要考虑到Q与K的位置关系。
2. 不同于Transformer的绝对位置编码，论文作者希望将原来从first input传入的position_embedding 转移到self-attention中，并希望模型能在训练的过程中学习到这相对位置编码参数，最后作出假设：Residual connections help propagate position information to higher layers.
3. 论文将token之间相对位置输入建模为一个有向的、全联接的图模型， 希望通过直接创建两组边关系aVij and aKij 分别适用于attention中的QK点积计算，与V与softmax结果的点积计算，由此可以避免一些多余的线性变换。
4. V与softmax结果的点积计算，将相对位置信息传递给下游任务：
   
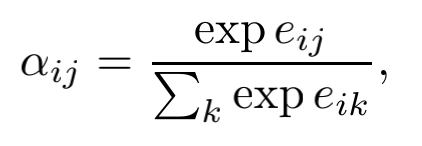
   This extension is presumably important for tasks where information about the edge types selected by a given attention head is useful to downstream encoder or decoder layers.
5. attention中的QK点积计算，通过相对位置信息影响注意力分布：
   
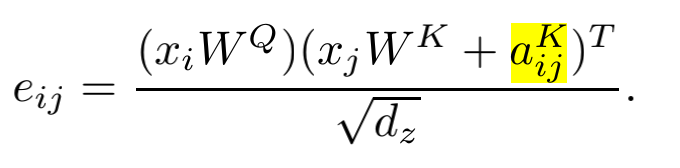
   model will consider edges when determining compatibility
6. 对相对位置编码距离进行截断，将其最大相对位置设置为固定值K：
   
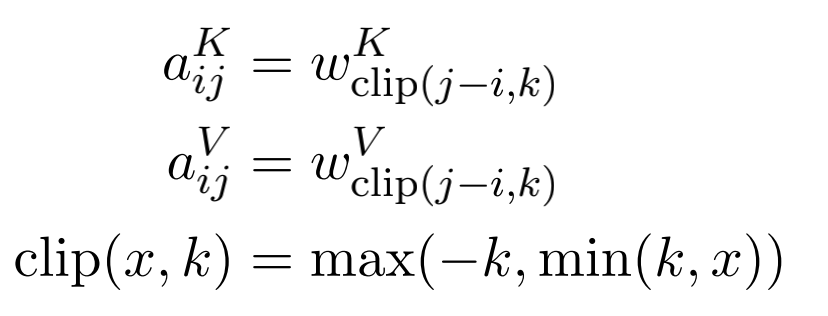
   We hypothesized that precise relative position information is not useful beyond a
   certain distance.
7. 更有效的计算：
   1. 多头attention共享一组相对位置编码，we reduce the space complexity of storing relative position representations from O(hn²da) to O(n²da) by sharing them across each heads. Additionally, relative position representations can be shared across sequences.
   2. 当不考虑相对位置编码时，原有的QKattend可以通过矩阵点积的方式实现并行计算，但当我们在eij的计算公式，对于不同的i 我们需要给不同的Wj 加上对应aij，这不利于用矩阵惩罚的广播机制，论文通过如下变换解决了并行计算的问题：
      
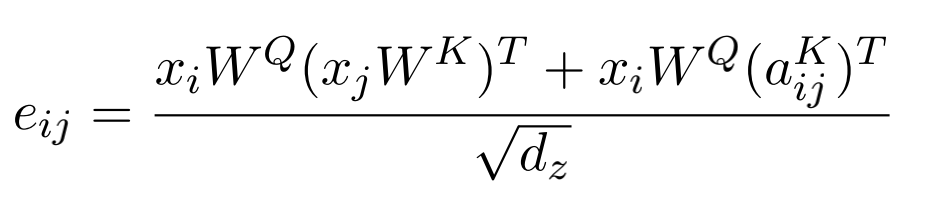
      式子的左半部分与原attention相同，可以通过矩阵乘法并行计算，观察式子的右半部分我们可以发现，对于eij部分的计算已经与K无关，我们可以分开计算两部分后再相加，右半部分我们可以通过 i 次并行的 j * d · d * 1 = j * 1 矩阵乘法得到可以与左半部分对位相加的 e_ij 矩阵，以此加快了模型的计算速度。
      勉强一看的示意图：
      

---

NEZHA

这里只阐述NEZHA的相对位置编码方法，模型的其他细节还是看论文来的实在啦～

1. 前言中也说道：Bert模型之所以限制了输入token的长度要小于512，原因在于bert的postition_embedding是与word_embedding相加后输入到encode层中，虽然与transformer一样，都是绝对位置编码，但bert的postition_embedding是初始化后可以训练的参数，在预训练过程中得到，因此固定的参数大小使得当给入一个大于512的postition_id后无法在embedding矩阵中找到对应的向量。
2. 因此可以思考，既然绝对位置编码的意义在于捕获token的相对位置关系，那么我们可以直接对token的相对位置进行编码，NEZHA模型就是在相对位置编码的基础上诞生的MLM预训练模型。
3. 与上一篇论文不同的是，NEZHA相对位置编码是sinusoidal functions计算出的固定值，这使得模型可以延展到处理更长长度的句子，具体如下：

4. That is, each dimension of the positional encoding corresponds to a sinusoid, and the sinusoidal functions for different dimensions have different wavelengths. In the above equations, dz is equal to the hidden size per head of the NEZHA model (i.e., the hidden size divided by the number of heads). The wavelengths form a geometric progression from 2π to 10000 · 2π. We choose the fixed sinusoidal functions mainly because it may allow the model to extrapolate to sequence lengths longer than the ones encountered during training.
5. 用 aij 表示 i 到 j 的相对位置编码，其本质是一个n维的向量。位置编码上每一维的值沿用了sinusoidal functions来计算，j 代表 Self-attention中Q的位置，i 代表K的位置，k表示该位置编码向量上的第k维，dz则与一个attention-head的hidden_size对齐，由此我们就构建好了相对位置编码矩阵，且该矩阵在训练过程中固定不变。
6. 论文沿用了Self-Attention with Relative Position Representations的相对位置编码在Attention中的计算方法。

---

How to build Relative Position

Tensorflow-GPU 2.0.0
Transformers 3.1.0

Get Relative Position Embedding

class Sinusoidal(tf.keras.initializers.Initializer):
    def __call__(self, shape, dtype=None):
        """
        Sin-Cos形式的位置向量
        用于创建relative position embedding
        后续通过计算位置差来对embedding进行查询 得到相对位置向量
        embedding的shape 为[max_k（最大距离）,deep（相对位置向量长度)]
        """
        vocab_size, depth = shape
        embeddings = np.zeros(shape)
        for pos in range(vocab_size):
            for i in range(depth // 2):
                theta = pos / np.power(10000, 2. * i / depth)
                embeddings[pos, 2 * i] = np.sin(theta)
                embeddings[pos, 2 * i + 1] = np.cos(theta)
        return embeddings
    
class RelativePositionEmbedding(tf.keras.layers.Layer):
	'''
	input_dim: max_k 对最大相对距离进行截断
	output_dim:与最后的eij相加,由于各个head之间共享相对位置变量，
	因此该参数为 hidden_size / head_num = head_size
	embeddings_initializer：初始化的权重，此处使用Sinusoidal()
	'''
    def __init__(
        self, input_dim, output_dim, embeddings_initializer=None, **kwargs
    ):
        super(RelativePositionEmbedding, self).__init__(**kwargs)
        self.input_dim = input_dim
        self.output_dim = output_dim
        self.embeddings_initializer = embeddings_initializer

    def build(self, input_shape):
        super(RelativePositionEmbedding, self).build(input_shape)
        self.embeddings = self.add_weight(
            name='embeddings',
            shape=(self.input_dim, self.output_dim),
            initializer = self.embeddings_initializer,
            trainable=False
            # 此处注意设置trainable = False 固定相对位置编码
        )

    def call(self, inputs):
    	'''
    	(l,l) 根据embedding查表得到相对位置编码矩阵 (l,l,d)
    	'''
        pos_ids = self.compute_position_ids(inputs)
        return K.gather(self.embeddings, pos_ids)

    def compute_position_ids(self, inputs):
    	'''
    	通过传入的hidden_size (b,l,h)
    	根据长度计算相对位置矩阵（l,l)(k个相对位置值）
    	'''
        q, v = inputs
        # 计算位置差
        q_idxs = K.arange(0, K.shape(q)[1], dtype='int32')
        q_idxs = K.expand_dims(q_idxs, 1)
        v_idxs = K.arange(0, K.shape(v)[1], dtype='int32')
        v_idxs = K.expand_dims(v_idxs, 0)
        pos_ids = v_idxs - q_idxs
        # 后处理操作
        max_position = (self.input_dim - 1) // 2
        
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63