【数据结构第五章】- 树_树在数据结构三种存储结构表示 习题

目录

一、树的定义

二、树的基本术语

三、树的存储结构 

3.1 - 双亲表示法

3.2 - 孩子表示法

3.3 - 孩子兄弟表示法

---

---

一、树的定义

树（Tree）是 n（n >= 0）个结点的有限集，它或为空树（n = 0）；或为非空树，对于非空树 T：

1. 有且仅有一个称之为根的结点；

2. 除根结点以外的其余结点可分为 m（m > 0） 个互不相交的有限集 T1, T2, ..., Tm，其中每一个集合本身又是一棵树，并且称为根的子树（SubTree）。

例如，在下图中，(a) 是只有一个根结点的树；(b) 是有 13 个结点的树，其中 A 是根，其余结点分成 3 个互不相交的子集；T1 = { B, E, F, K, L }，T2 = { C, G }，T3 = { D, H, I, J, M }。T1、T2 和 T3 都是根 A 的子树，且本身也是一棵树。例如 T1，其根为 B，其余结点分为两个互不相交的子集：T11 = { E, K, L }，T2 = { F }。T11 和 T12 都是 B 的子树。而 T11 中 E 是根，{ K } 和 { L } 是 E 的两棵互不相交的子树，其本身又是只有一个根结点的树。

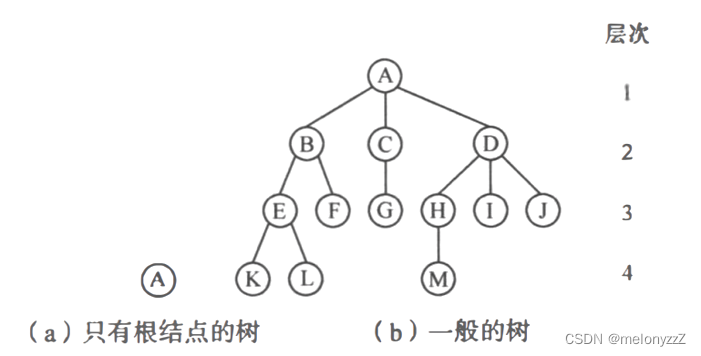
树的结构定义是一个递归的定义，即在树的定义中又用到树的定义，它道出了树的固有特性。

根据定义可知，除了根结点以外，任何一个结点都有且仅有一个双亲结点。

---

二、树的基本术语

• 结点：树中的一个独立单元。包含一个数据元素及若干指向其子树的分支。

• 结点的度：结点拥有的子树数为结点的度。

• 树的度：树的度是树内各结点度的最大值。

• 叶子：度为 0 的结点称为叶子或终端结点。

• 非终端结点：度不为 0 的结点称为非终端结点或分支结点。除根结点以外，非终端结点也称为内部结点。

• 结点的层次：结点的层次从根开始定义，根为第一层，根的孩子为第二层。树中任一结点的层次等于其双亲结点的层次加 1。

• 树的深度：树中结点的最大层次称为树的深度或高度。

• 双亲和孩子：结点的子树的根称为该结点的孩子，相应地，该结点称为孩子的双亲。

• 兄弟：同一个双亲的孩子之间互称兄弟。

• 祖先：从根到该结点所经分支上的所有结点。

• 子孙：以某结点为根的子树中的任一结点都称为该结点的子孙。

• 堂兄弟：双亲在同一层的结点互为堂兄弟。‘

• 有序树和无序树：如果将树中结点的各子树看成从左至右是有次序的（即不能互换），则称该树为有序树，否则称为无序树。在有序树中最左边的子树的根称为第一个孩子，最右边的称为最后一个孩子。

• 森林：是 m（m >= 0）棵互不相交的树的集合。对于树中每个结点而言，其子树的集合即为森林。由此，也可以用森林和树相互递归的定义来描述树。

---

三、树的存储结构 

在大量的应用中，人们曾使用多种形式的存储结构来表示树。下面介绍 3 种常用的表示方法。

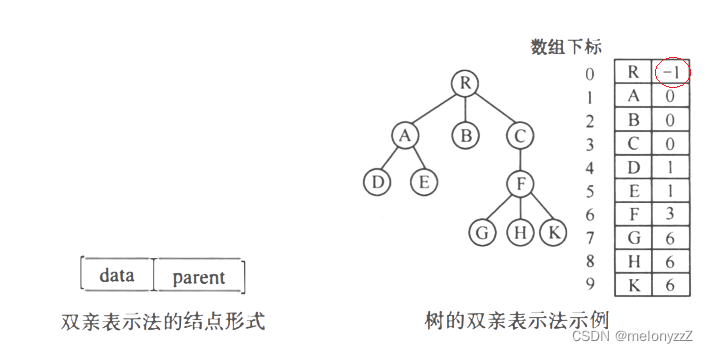
3.1 - 双亲表示法

这种表示方法中，以一组连续的存储单元存储树的结点，每个结点除了数据域 data 外，还附设一个 parent 域用以指示其双亲结点的位置。

// 结点结构
typedef struct
{
    DataType data;
    int parent;  // 双亲结点的位置
}PTNode;
 
// 树结构
typedef struct
{
    PTNode* nodes;  // 动态的结点数组
    int size;  // 结点数
    int capacity;  // 容量
    int root;  // 根结点的位置
}PTree;

这种存储结构利用了每个结点（除根以外）只有唯一的双亲的性质。在这种存储结构下，求结点的双亲十分方便，也很容易求树的根，但求结点的孩子时需要遍历整个结构。

3.2 - 孩子表示法

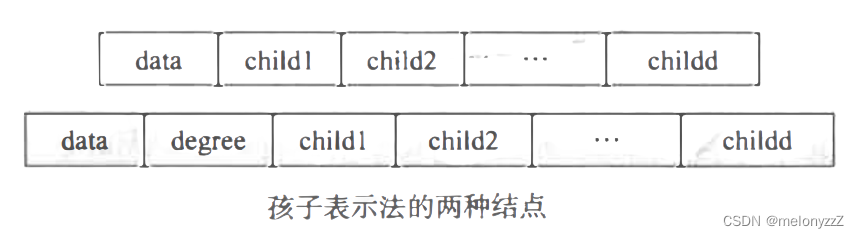
由于树中每个结点可能有多棵子树，则可用多重链表，即每个结点有多个指针域，其中每个指针指向一棵子树的根结点。此时链表中的结点可以有如下图所示两种结点格式。

1. 若采用第一种结点格式，则多重链表中的结点是同构的，其中 d 为树的度。由于树中很多结点的度小于 d，所以链表中有很多空链域，空间较浪费。不难推出，在一棵有 n 个结点、度为 k 的树中必有 n(k - 1) + 1 个空链域。

2. 若采用第二种结点格式，则多重链表中的结点是不同构的，其中 d 为结点的度，degree 域的值同 d。此时，虽然能节约存储空间，但操作不方便。

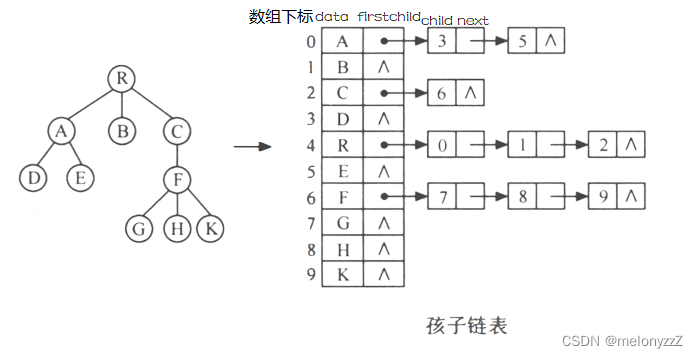
另一种办法是，把每个结点的孩子结点排列起来，看成是一个线性表，且以单链表做存储结构，则 n 个结点有 n 个孩子链表（叶子结点的孩子链表为空表）。而 n 个头指针又组成一个线性表，为了便于查找，可采用顺序存储结构。

// 孩子结点
typedef struct CTNode
{
    int child;
    struct CTNode* next;
}CTNode, *ChildPtr;
 
// 双亲结点
typedef struct
{
    DataType data;
    ChildPtr firstchild;
}CTBox;
 
// 树结构
typedef struct
{
    CTBox* nodes;  // 动态的结点数组
    int size;  // 结点数
    int capacity;  // 容量
    int root;  // 根结点的位置
}CTree;

与双亲表示法相反，孩子表示法便于那些涉及孩子的操作的实现。可以把双亲表示法和孩子表示法结合起来，即将双亲表示法和孩子链表合在一起。如下图所示。

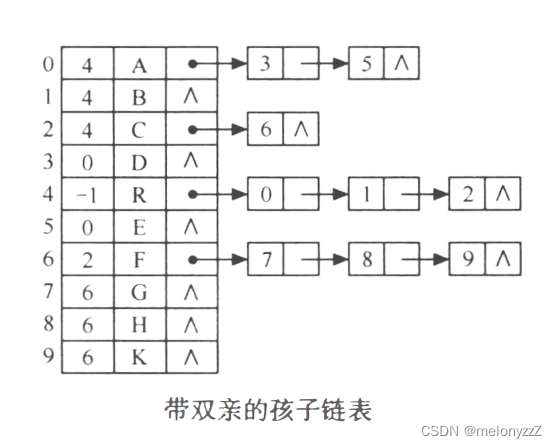
3.3 - 孩子兄弟表示法

又称二叉树表示法，或二叉链表表示法，即以二叉链表做树的存储结构。链表中结点的两个指针域分别指向该结点的第一个孩子结点和下一个兄弟结点，分别命名为 firstchild 域和 nextsibiling 域。

typedef struct CSNode
{
    DataType data;
    CSNode* firstchild;
    CSNode* nextsibling;
}CSNode, *CSTree;

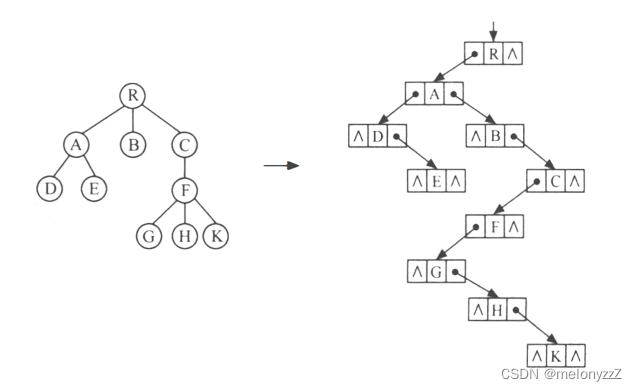
上图所示为树的孩子兄弟链表。利用这种存储结构便于实现各种树的操作。首先易于实现找结点孩子等操作。例如，若要访问结点 x 的第 i 个孩子，则只要先从 firstchild 域找到第一个孩子结点，然后沿着孩子结点的 nextsibling 域连续走 i - 1 步，便可找到 x 的第 i 个孩子。当然，如果为每个结点增设一个 parent 域，则同样能方便地实现查找双亲的操作。

这种存储结构的优点是它和二叉树的二叉链表表示完全一样，便于将一般的树结构转换为二叉树进行处理，利用二叉树的算法实现对树的操作。因此孩子兄弟表示法是应用较为普遍的一种树的存储表示方法。