回归分析：最小二乘法估计线性回归模型的参数_spss最小二乘法估计参数

一、一元线性回归

回归分析可以用来分析变量间的关联强度和关联方向，而且还可以通过回归方程式，利用已知的自变量预测未知的因变量。

一元线性回归又称简单线性回归，是只包括一个自变量和一个因变量，而且二者的关系可以用一条直线近似表示，会建立出一个一元线性回归方程。设为

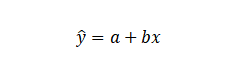
二、最小二乘法求一元线性回归方程

回归分析中要确定一个一元线性回归方程，很简单，只需要通过样本数据求出公式中a和b两个参数的值，一元线性回归方程就唯一确定。

a和b如何确定，有一种比较好的计算方法，叫做最小二乘法。这里以一个简单小案例具体介绍如何用最小二乘法估计参数a和b。

案例数据：为了研究受教育年限和职业声望之间的关系，得到了8个抽样调查结果如下：

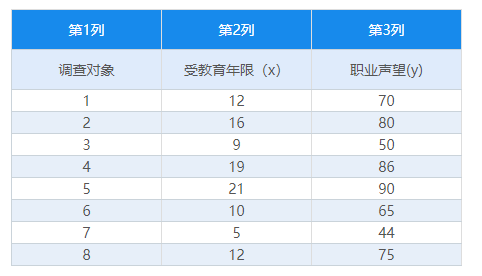
首先分析样本数据，先绘制一个散点图，看看数据的分布情况，这里将数据整理成上方表格的形式，上传到SPSSAU，上传成功如下图所示，【受教育年限】为自变量，【职业声望】为因变量：

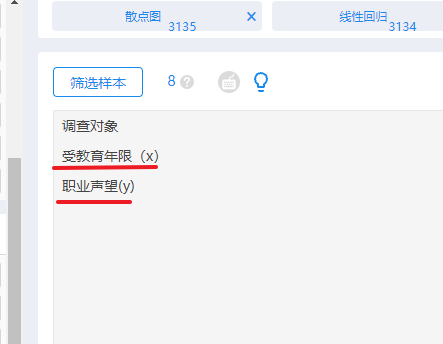
选择【可视化】板块中的【散点图】，以受教育年限】和【职业声望】两个变量的数据来绘制散点图：

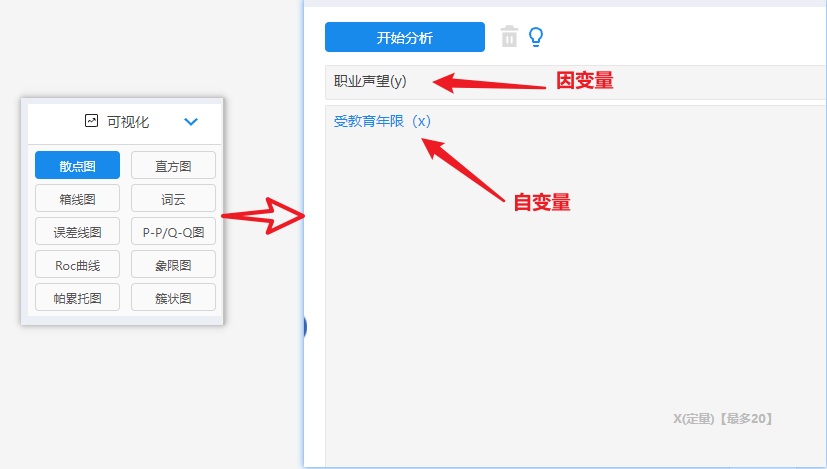
输出散点图：

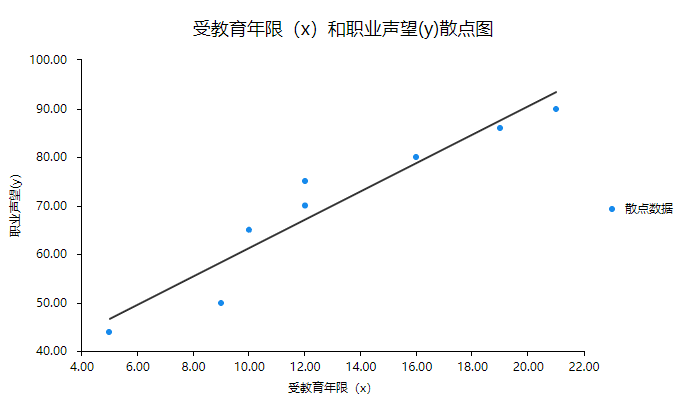
由散点图可见，职业声望（Y）随受教育年限（X）的增加而增加，且这些点呈直线趋势，所以我们可以求出一条最能代表这8个数据分布点分布趋势的直线：

不妨设为：

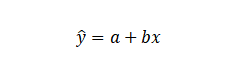
使用最小二乘法对这个直线回归方程中的参数a和b进行估计:

公式如下：

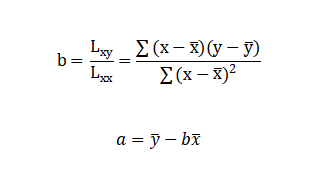
具体求法：

第一步：求出变量x的平均值

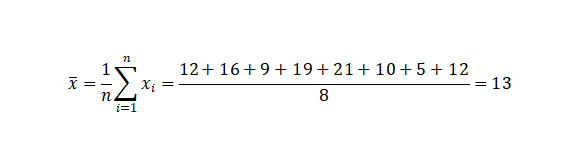
第二步：求出变量y的平均值

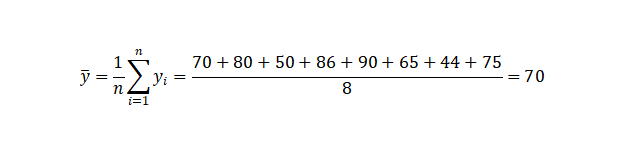
第三步：求出系数b

第四步：求出截距a

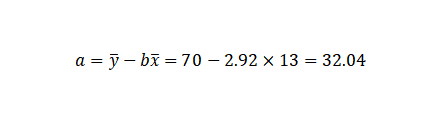
这样就得到了一元线性回归方程：

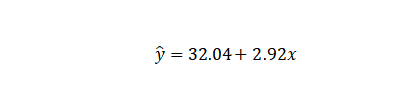
三、SPSSAU线性回归分析

需要对数据进行线性回归分析，可以使用SPSSAU，快速完成数据分析，在【通用方法】中选中【线性回归】方法，将【受教育年限】与【职业声望】分别放入对应分析框中，点击【开始分析】可一键输出结果，如下图：

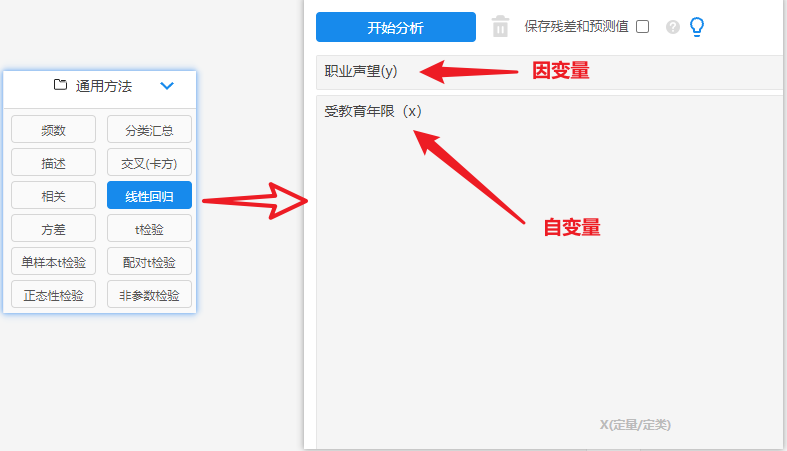
输出结果：

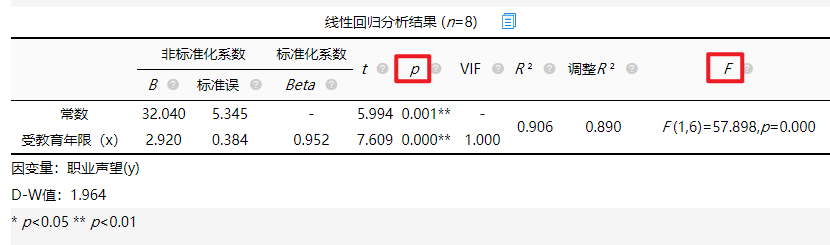
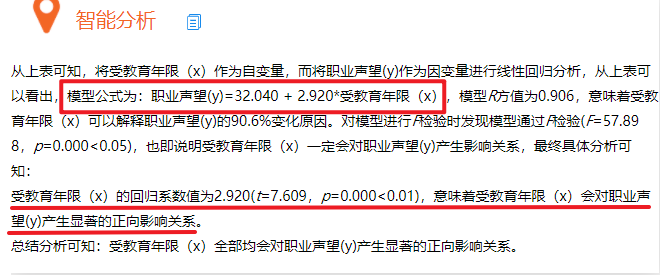
智能分析：由文字分析可知，SPSSAU算出的线性回归模型公式和我们之前手算的公式完全一样，另外自动分析出受教育年限会对职业声望产生显著的正向影响关系。

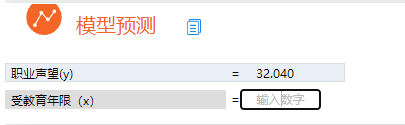
模型预测：另外还提供简单线性回归的模型预测，输入自变量【受教育年限】的值，系统会自动预测【职业声望】的值。如下图：

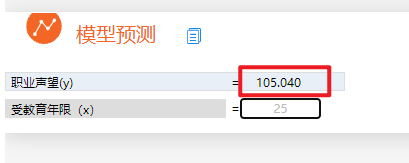
此时我们预测受教育年限为25时的职业声望，如下图：

另外可以通过线性回归的方差分析检验回归模型：

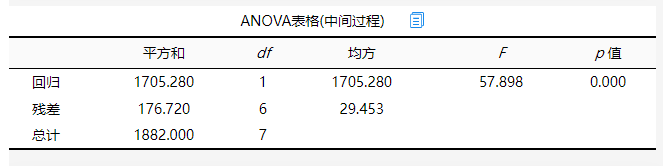
方差分析可知，对模型进行F检验时发现模型通过F检验(F=57.898，p=0.000<0.05)，也即说明模型构建有意义。