transformer详解

框架

基本结构

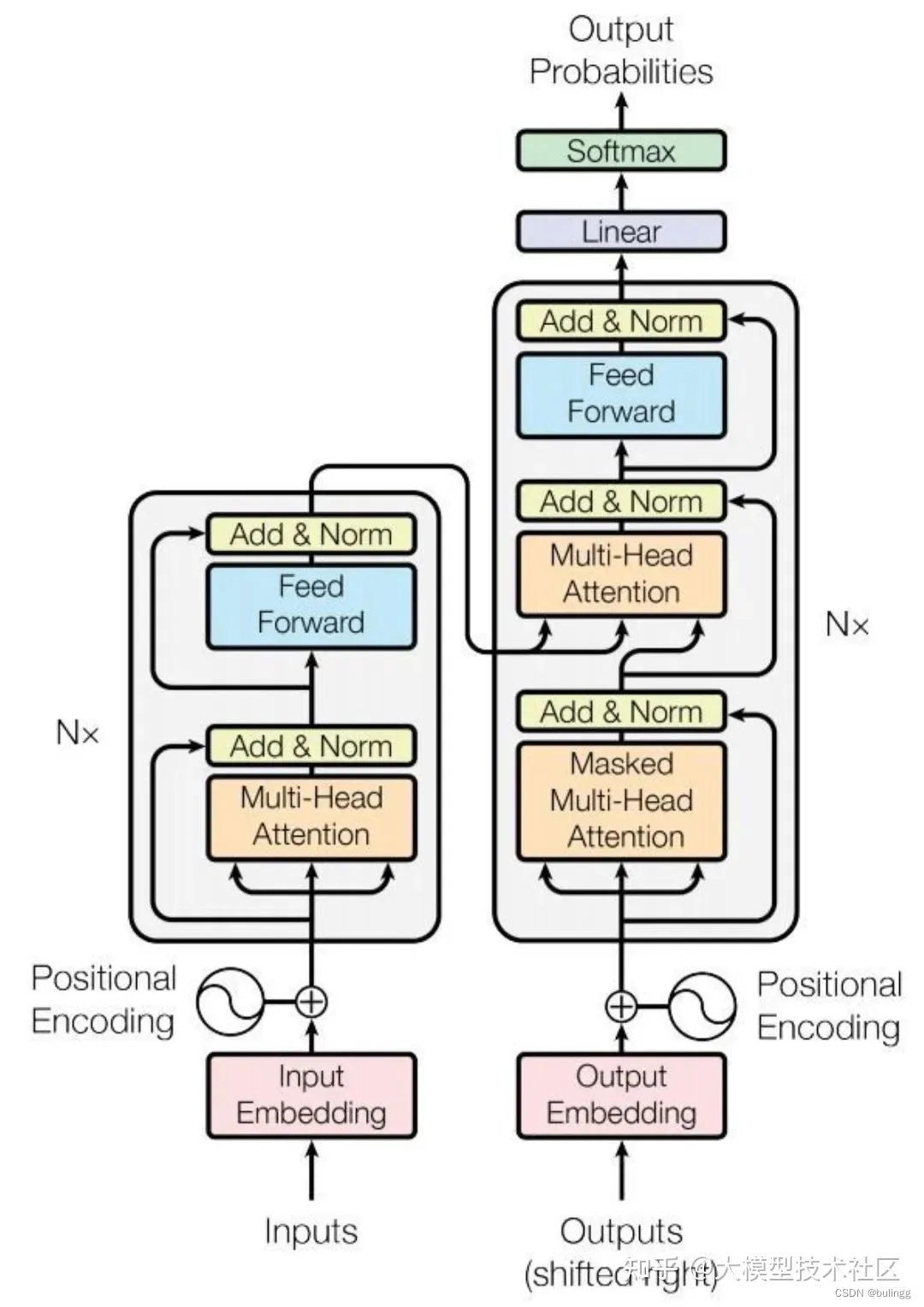
transformer主要分为两个部分，包括Encoder和Decoder，其中Encoder对输入信息编码，Decoder结合输出对输入信息进行解码。
Encoder的输入由Input Embedding和位置嵌入Position Embedding求和输入encoder中的block中，包括multi-head attention中，然后经过Add & Layer normalization，再经过feed forward进行输入，然后经过Add & Layer normalization
Decoder的输入也是由output embedding和position embedding组成，decoder中的block相较于encoder而言，增加了一个masked multi-head attention，确保模型仅看到当前步及以前的信息

注意力机制

三要素：查询（query），键（key），值（value）
通过query序列检索key，获取合适的value信息

注意力评分函数(scoring function)

假设有一个查询 $q\in {\mathcal{R}}^q$和$m$个键值对$(k_1,v_1),\cdots ,(k_m,v_m)$，$k\in {\mathcal{R}}^k,v\in {\mathcal{R}}^v$
注意力函数可表示为加权和的形式：
$$f(q,(k_1,v_1),\cdots ,(k_m,v_m))=\sum _{i=1}^m\alpha (q,k_i)v_i\in {\mathcal{R}}^v$$
其中$\alpha (q,k_i)$是由注意力评分函数$a$通过$softmax$函数归一化得到
$$$\alpha (q,k_i)=softmax(a(q.k_i))=\frac{exp(a(q,k_i))}{{\sum }_j^{m}exp(a(q,k_j))}$$
$a$有以下几种形式：

• 加性注意力(Additive Attention)：(当query，key为不同长度的矢量时)
  $$a(q,k_i)=W_v^{T}tanh(W_{q}q+W_{k}k)\in \mathcal{R}$$
  其中，$W_q\in {\mathcal{R}}^{h\times q},W_k\in {\mathcal{R}}^{h\times k},W_v\in {\mathcal{R}}^{h\times 1}$
  即，将查询和键连结起来后输入到一个多层感知机（MLP）中， 感知机包含一个隐藏层，其隐藏单元数$h$是一个超参数，$tanh$作为激活函数，并禁用偏置项（即使添加了偏置项，即$tanh(X+b)$，在经过$softmax$归一化时会被消除，仍然无效）
• 点积注意力(Dot Product Attention )：（要求query和key长度相同）
  $$a(q,k_i)=q^T{k}_i$$
• 缩放点积注意力(Scaled Dot-Product Attention):$q,k_i\in R^{d_k}$，并假设其中的元素均为0均值，1方差
  $$a(q,k_i)=q^{T}k/\sqrt{d}$$
  当query和key的维度$d_k$较小时，点积注意力和加性注意力表现效果相似，但是当$d_k$较大时，方差也会变大($D(q\cdot k)=d_k$)，分布趋于陡峭，当点积的数据量级较大时，经过$softmax$后，梯度会很小，容易导致梯度消失，不利于计算，需要进行一定的缩放，将其方差控制为1。
  证明可见：self-attention中的dot_product为什么要被缩放

除以$d_k$的原因

1. 防止输入softmax的值过大，导致偏导数趋近于0，避免梯度消失
2. 使得$q\cdot k$的值满足期望为0，方差为1的分布

Scaling的作用
1 防止梯度消失
在计算注意力得分时，如果不进行缩放，随着序列长度的增加，点积的值可能会变得非常大，导致softmax函数的梯度接近于0，从而引起梯度消失问题。通过缩放点积的结果，可以减少这种效应，确保梯度的稳定。
2 维持数值稳定性
Scaling有助于保持模型在训练过程中的数值稳定性。通过除以维度的平方根，可以使得得分分布的方差维持在一个合理的范围内，避免因为数值过大导致的计算问题，如浮点数溢出。
3 提高优化效率
适当的缩放可以使得优化过程更加高效。它有助于梯度下降算法更快地找到损失函数的极小值，因为缩放后的得分范围更适合softmax函数处理，从而加速了模型的收敛速度。

当实际应用一个批量数据进行运算时，基于$n$个查询和$m$个键-值对计算注意力，其中查询，键长度为$d$，值长度为$v$，则$Q\in {\mathcal{R}}^{n\times d}，K\in {\mathcal{R}}^{m\times d},V\in {\mathcal{R}}^{m\times v}$的缩放点击注意力为：
$$softmax(\frac{Q{K}^T}{\sqrt{d}})V\in {\mathcal{R}}^{n\times v}$$

区别：Dot Product Attention 和 Additive Attention两者在复杂度上是相似的。但是Additive Attention增加了三个可学习的矩阵，所以相比另外两个效果会更好，同时也增加了更多的模型参数，计算效率会较低。

自注意力机制（self-attention）

查询、键、值均由同一个输入经过不同的“线性投影”变化得到，并采用缩放点积注意力得到最终输出
$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d}})V\in {\mathcal{R}}^{n\times v}$$

masked self-attention

作用：防止Transformer在训练时泄露后面的它不应该看到的信息，确保仅看到当前及以前得信息

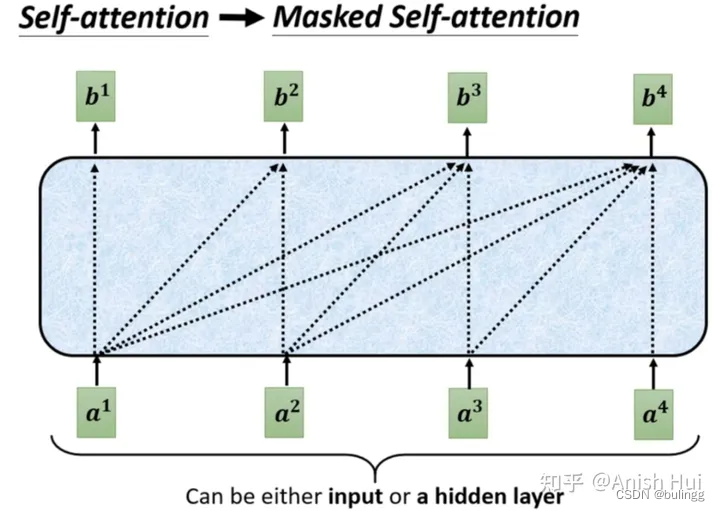
更多可见：MultiHead-Attention和Masked-Attention的机制和原理

多头注意力（multi-head attention）

原理：在给定相同的查询、键、值时，使用**h个独立的"线性投影"**来变换q,k,v，然后并行得使用h个注意力机制，学习到不同的行为，然后将h个自注意力的输出拼接在一起，通过另一个可学习的线性投影进行变换，产生最终的输出，来捕捉序列内各种范围内的依赖关系（例如短距离依赖和长距离依赖）
其中，每个自注意力被称为一个头

• 作用：将模型分为多个头，期望形成多个相互独立的子空间，可以让模型关注不同的信息

Transformer多头注意力的物理意义

1. 多样性的表示学习
   多头注意力机制允许模型在不同的表示子空间中并行地学习信息。每个“头”可以被看作是一个独立的注意力学习模块，它能够捕捉序列内不同种类的特征，例如不同级别的语法结构和语义信息。这种设计在物理意义上类似于人类大脑的并行处理机制，能够同时处理多种类型的信息
2. 增强模型的关注能力
   在物理意义上，多头注意力机制模仿了人类在处理信息时的注意力分配。就像人类会在阅读或听别人说话时关注不同的信息点，多头注意力允许模型同时关注序列中的多个位置，从而更好地理解上下文和抓住关键信息。
3. 提高模型的泛化能力
   每个注意力头学习到的信息都是不同的，这种差异性使得模型在整合各个头的输出时能够获得更加丰富和全面的信息。在物理意义上，这类似于从不同角度观察问题，能够提供更全面的视角，从而增强模型对新数据的泛化能力。

总结来说，Transformer中的多头注意力机制在物理意义上代表了一种并行和多角度的信息处理方式，它通过模拟人类的注意力分配和信息处理机制，提高了模型对序列数据的表示能力和理解深度。

import torch
from torch import nn

##### 使多个头可以进行并行计算，p_q = p_k = p_v = p_o/h，p_o=num_hiddens，
# 直接用nn.Linear(query_size,num_hiddens),num_hiddens=p_v*h，即多个线性变换结合在一起

 # 假设输出维度为num_hiddens,同时h*p_v = num_hiddens
def transpose_qkv(X, num_heads): # 将组合起来的输入，变换为num_heads个输入
    # 输入X的shape为(batch_size,查询或者“键值对”的个数，num_hiddens)
    # 输出X的shape为(batch_size,查询或者“键值对”的个数，num_heads，num_hiddens/num_heads) 
    X = X.reshape(X.shape[0],X.shape[1], num_heads,-1)
    # 输出X的形状:(batch_size，num_heads，查询或者“键－值”对的个数,
    # num_hiddens/num_heads)
    X = X.permute(0,2,1,3)
    # 最终输出的形状:(batch_size*num_heads,查询或者“键－值”对的个数,
    # num_hiddens/num_heads)
    return X.reshape(-1,X.shape[2],X.shape[3])

def transpose_output(X,num_heads): # 将组合起来的输出，变换为num_heads个输出
    """逆转transpose_qkv函数的操作"""
    X = X.reshape(-1,num_heads,X.shape[1].X.shape[2])
    X = X.permute(0,2,1,3)
    return X.reshape(X.shape[0], X.shape[1],-1)
    
    
class MultiHeadAttention(nn.Module):
    def __init__(self,key_size,query_size,value_size,num_hiddens,num_heads,dropout,bias=False,**kwargs)
    super(MultiHeadAttention,self).__init__(**kwargs)
    self.num_heads = num_heads
    self.attendtion = DotProductAttendtion(droupout)
    self.W_q = nn.Linear(query_size,num_hiddens, bias)
    self.W_k = nn.Linear(key_size,num_hiddens, bias)
    self.W_v = nn.Linear(value_size,num_hiddens, bias)
    self.W_o = nn.Linear(num_hiddens,num_hiddens, bias)
    
   def forward(self,queries, keys, values, valid_lens):
    # queries，keys，values的形状:
        # (batch_size，查询或者“键－值”对的个数，num_hiddens)
    # valid_lens　的形状:
        # (batch_size，)或(batch_size，查询的个数)
    # 经过变换后，输出的queries，keys，values　的形状:
        # (batch_size*num_heads，查询或者“键－值”对的个数，
        # num_hiddens/num_heads)
        
    queries = transpose_qkv(self.W_q(queries),self.num_heads)
    keys = transpose_qkv(self.W_k(keys),self.num_heads)
    values = transpose_qkv(self.W_v(values),self.num_heads)
    
    if valid_lens is not None:
        # 按行重复num_heads遍
        valid_lens = torch.repeat_interleave(
                valid_lens, repeats=self.num_heads, dim=0)
    
    output = self.attention(queries,keys, values,valid_lens)
    
    output_concat = transpose_output(output, self.num_heads)
    return self.W_o(output_concat)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

位置编码

作用：self-attention能够看到全局信息，忽略了顺序关系，为了使用序列的顺序信息，通过在输入表示中添加位置编码（positional encoding）来注入绝对的或相对的位置信息

假设输入$X\in {\mathcal{R}}^{n\times d}$表示一个序列中$n$个词元的$d$维嵌入表示。位置编码使用与输入$X$相同形状的位置嵌入矩阵$P\in {\mathcal{R}}^{n\times d}$表示

固定位置编码：
$$P_{i,2j}=sin(\frac{i}{10000^{2j/d}})$$
$$P_{i,2j+1}=cos(\frac{i}{10000^{2j/d}})$$
即对于每个词元，奇数维度采用$cos$函数，偶数维度采用$sin$函数
包含以下两种信息

• 绝对位置信息：（$i,j$分别表示词元在序列中的位置、位置编码的维度）

• 相对位置信息：
  对于任何确定的位置偏移$\delta$，位置处$i+\delta$的位置编码可以线性投影位置$i$处的位置编码来表示。
  $(P_{i,2j},p_{i,2j+1})\to (p_{i+\delta },p_{i+\delta ,2j+1}))$
  

缺点：当词嵌入维度较大时，较大维度的位置编码值完全一致

Layer normalization

因为神经网络的Block大部分都是矩阵运算，一个向量经过矩阵运算后值会越来越大，为了网络的稳定性，我们需要及时把值拉回正态分布。归一化的方式可以分为：

• BatchNorm就是通过对batch size这个维度归一化来让分布稳定下来。
• LayerNorm则是通过对Hidden size这个维度归一化来让某层的分布稳定。独立于batch size的算法，所以无论样本数多少都不会影响参与LN计算的数据

作用：神经网络的学习过程中，对于神经网络中间的每一层，其前面层的参数在学习中会不断改变，导致其输出也在不断改变，不利于这一层及后面层的学习，学习收敛速度会变慢，就会出现Internal Covariate Shift（内部协变量偏移）. 随着网络的层数不断增大，这种误差就会不断积累，最终导致效果欠佳。

更多可见Batch normalization和Layer normalization

Resnet（Add）

1. 在模型能够收敛的情况下，网络越深，模型的准确率越低，同时，模型的准确率先达到饱和，此后迅速下降。称之为网络退化（Degradation），resnet能够有效训练出更深的网络模型（可以超过1000层），使得深网络的表现不差于浅网络，避免网络退化。
2. 避免梯度消失/爆炸（主要通过归一化初始化和中间规归一化层来解决）

结构如下：

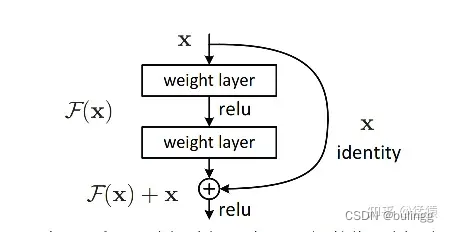
使数据可以跨层流动，残差模块的输出为：
$$H(x)=F(x)+x$$
其中，$F(x)$为残差函数，在网络深层的时候，在优化目标的约束下，模型通过学习使得逼近0（residule learning)，让深层函数在学到东西的情况下，又不会发生网络退化的问题。

更多可见：ResNet（残差网络）几个关键问题的理解

Feed Forward

结构：全连接神经网络，由多个相互连接的隐藏层组成，每一层通过线性变化，激活函数以及dropout等处理
作用：通过非线性变换，先将数据映射到高纬度的空间再映射到低纬度的空间，提取了更深层次的特征

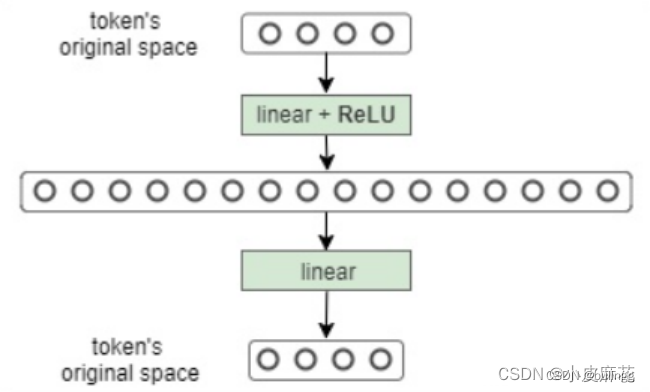
输入是multi-head attention的输出做了残差连接和norm之后的数据
前馈线性层只做了四件事情：

• 对文本中的每个位置(用向量表示)，进行逐位置的线性计算。
• 对线性运算的输出应用ReLU函数。
• 对上一步骤ReLU运算的输出进行再一次线性运算。
• 最后，将其添加到第 3 层的输出中。
  $$FFn(x)=W_2(max(0,W_{1}x+b_1))+b_2$$

作用
1 非线性变换
FFN为Transformer模型提供了非线性处理能力。它通常由两层线性变换组成，中间夹杂着一个非线性激活函数（如ReLU或GELU）。这种结构使得模型能够学习到更加复杂的特征表示。
2 增加模型容量
FFN增加了模型的参数量，从而扩展了模型的容量。这使得模型能够拟合更复杂的数据分布，并有助于提高模型的表达能力。
3 位置独立的特征处理
与注意力机制不同，FFN对序列中的每个位置进行相同的操作，这意味着它是位置无关的。这种设计有助于模型捕捉位置独立的特征，并且为模型引入了额外的非线性。