GAMES101学习笔记_games101笔记

变换Transformation

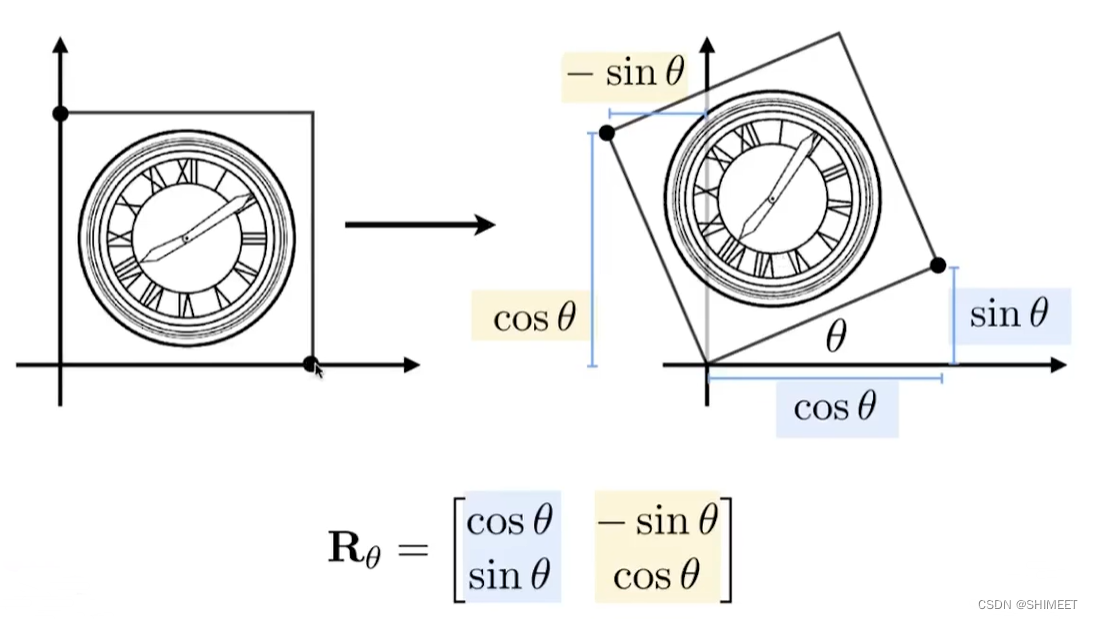
2D Transformations

• 旋转矩阵
  

• 仿射变换
  先线性变换，再平移变换

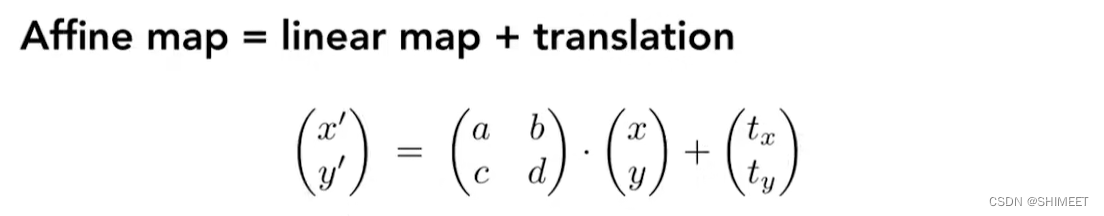
• 齐次坐标描述的矩阵

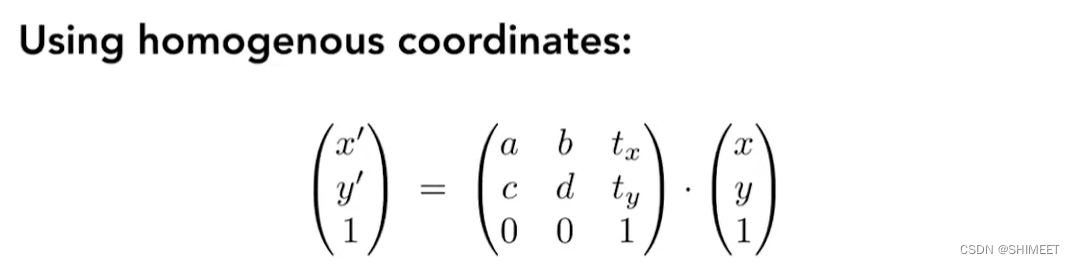
• 当w=0时，代表向量；当w≠0时，代表点(x/w, y/w, 1)

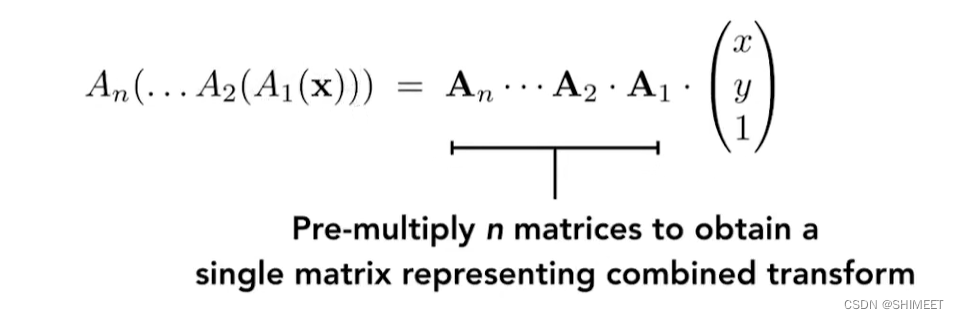
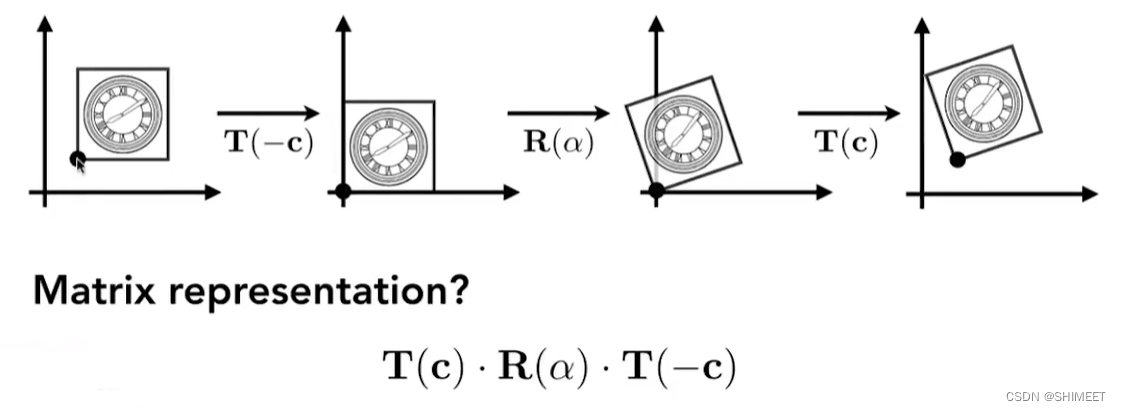
• 组合变换时，先缩放，再旋转，最后平移【矩阵乘法不满足交换律，但是满足结合律】

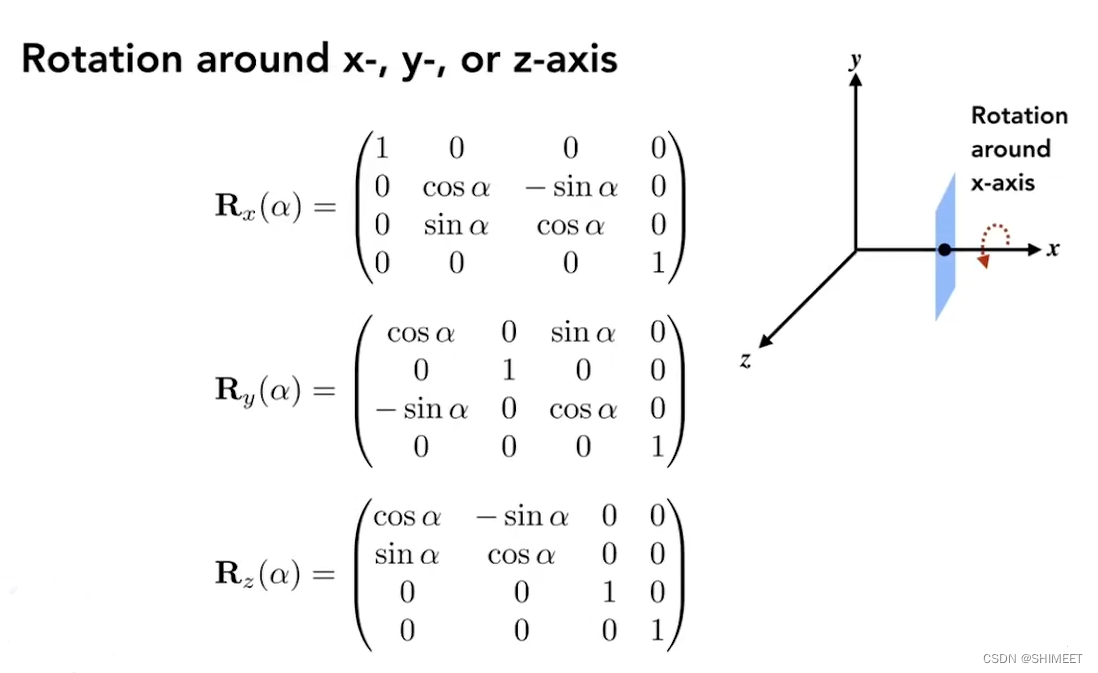
3D Transformations

• 旋转矩阵是正交矩阵
• 旋转矩阵的逆=旋转矩阵的转置，即(Rθ)T=(Rθ)-1

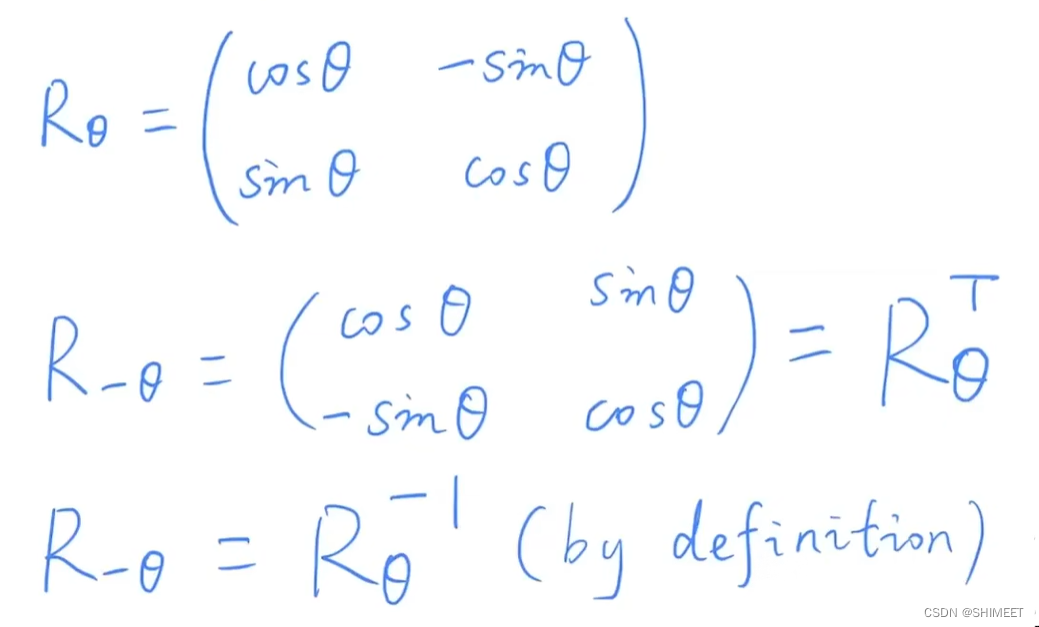
Viewing(观测) Transformation

• View(视图)/Camera transformation
• Projection(投影) transformation
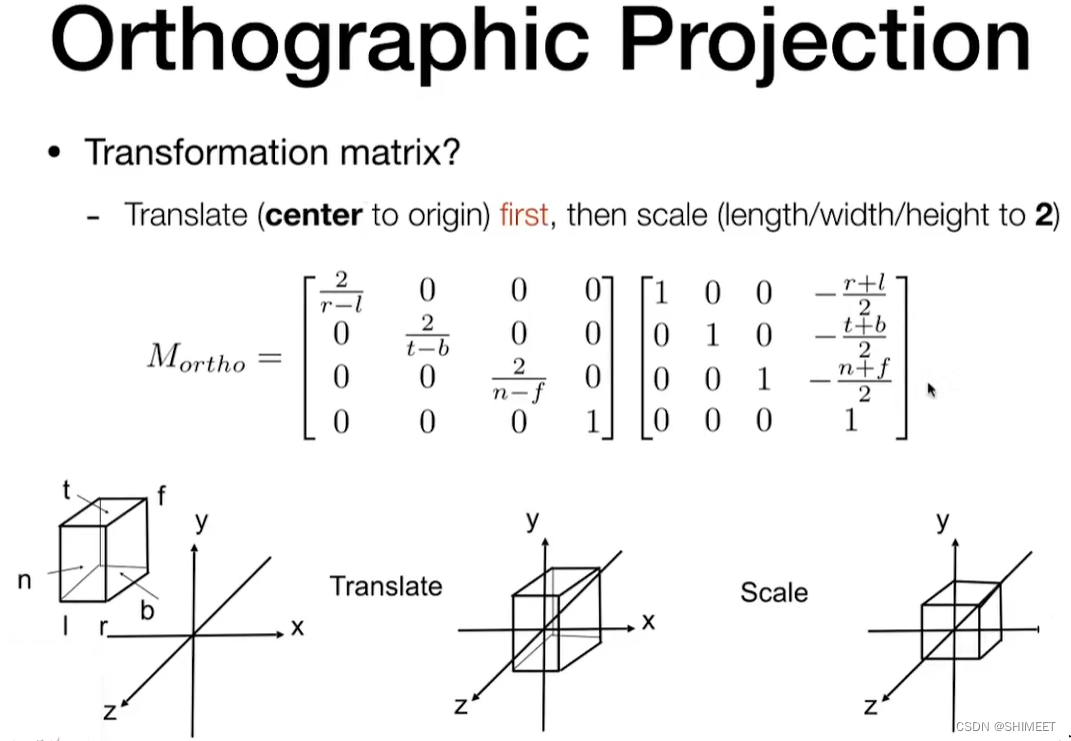
  Orthographic(正交) projection
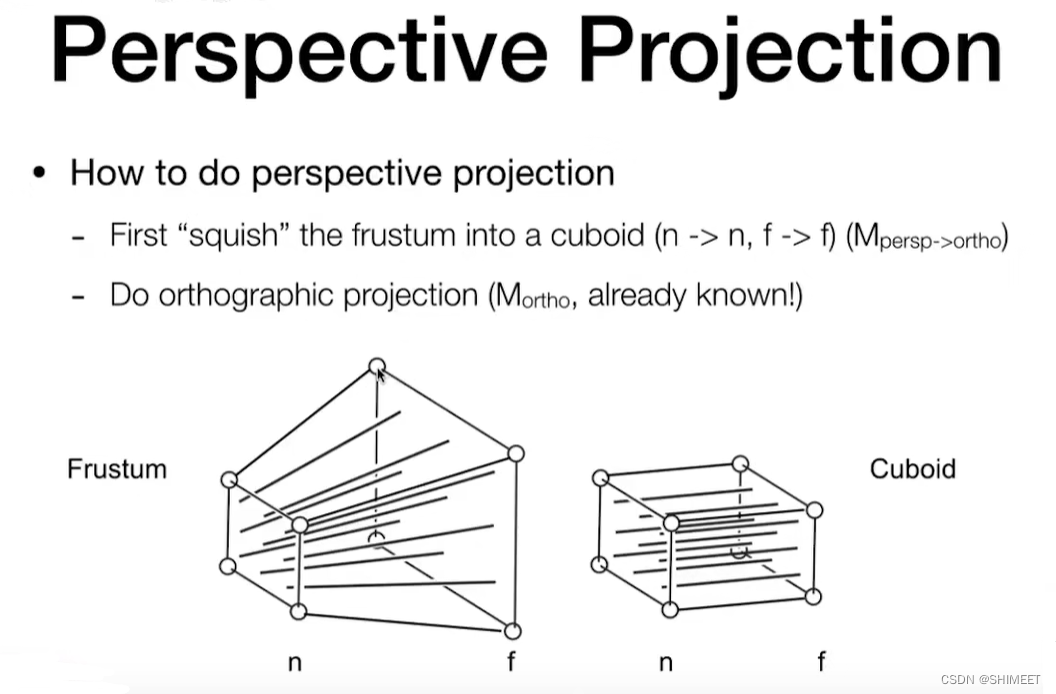
  Perspective(透视) projection

y不同的原因：右手坐标系，【Y = Z x X】 ≠ 【Y = X x Z】

Rodrigues’ Rotation Formula 任意旋转矩阵，分解在3个轴

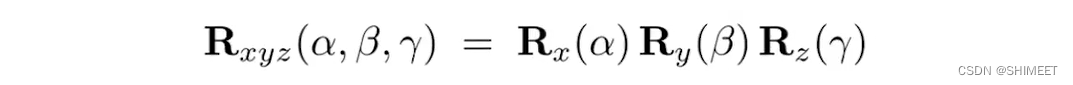
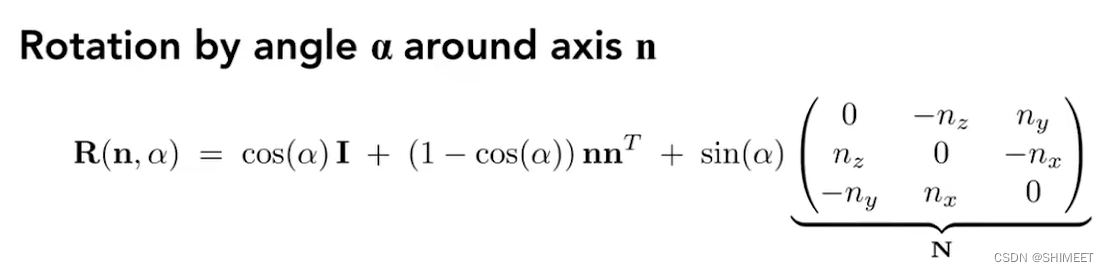
Viewing/Camera Transformation

相机位于原点，up轴为Y轴，朝向为-Z轴

Orthographic projection

Perspective projection

先"挤压"成正交投影，然后再执行正交投影

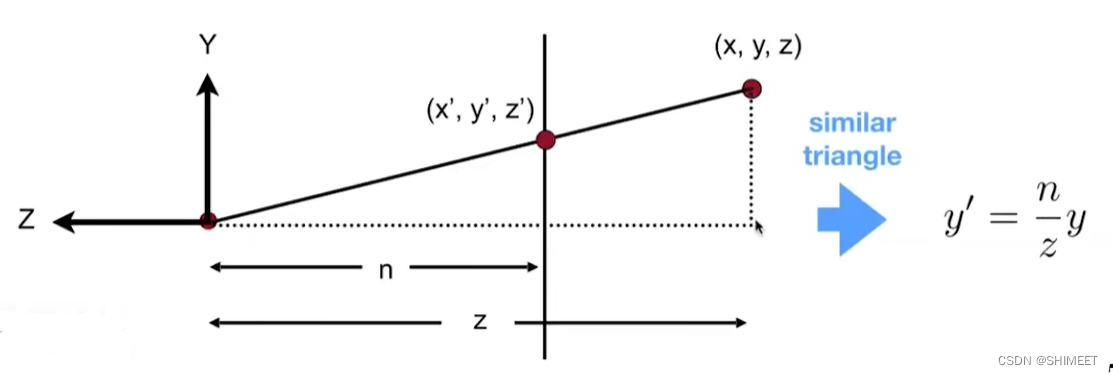
根据相似三角形得到


根据最近面上z不变得到

根据最远面上中心点位置不变得到

求解得到