leedcode——图数据结构相关3_给定一个有n个顶点和m条边的图,边的长度或距离(如下所示)。没有两条边连接 相同的

51. 检查边长度限制的路径是否存在

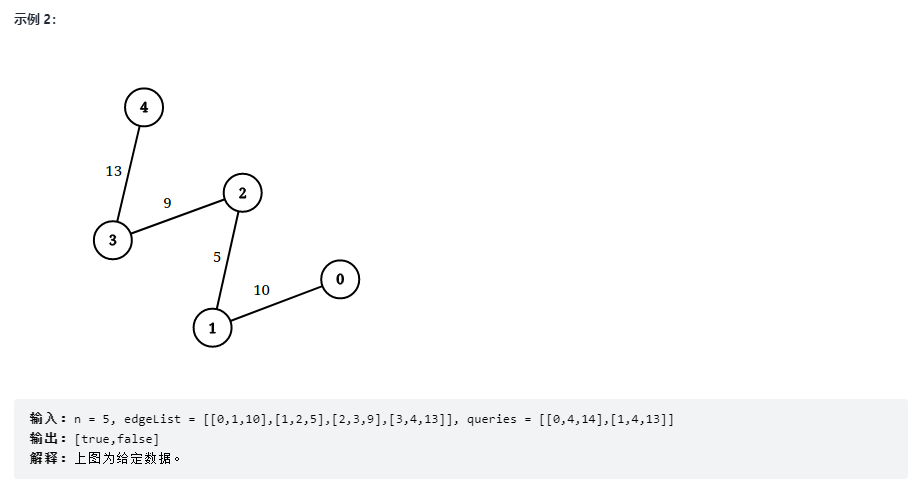
给你一个 n 个点组成的无向图边集 edgeList ，其中 edgeList[i] = [ui, vi, disi] 表示点 ui 和点 vi 之间有一条长度为 disi 的边。请注意，两个点之间可能有 超过一条边 。

给你一个查询数组queries ，其中 queries[j] = [pj, qj, limitj] ，你的任务是对于每个查询 queries[j] ，判断是否存在从 pj 到 qj 的路径，且这条路径上的每一条边都 严格小于 limitj 。

请你返回一个 布尔数组 answer ，其中 answer.length == queries.length ，当 queries[j] 的查询结果为 true 时， answer 第 j 个值为 true ，否则为 false 。

解法：离线思想+并查集检测连通性

感觉这是力扣第一次出离线思维的题目。

离线的意思是，对于一道题目会给出若干询问，而这些询问是全部提前给出的，也就是说，你不必按照询问的顺序依次对它们进行处理，而是可以按照某种顺序（例如全序、偏序（拓扑序）、树的 DFS 序等）或者把所有询问看成一个整体（例如整体二分、莫队算法等）进行处理。

与离线相对应的是在线思维，即所有的询问是依次给出的，在返回第 k 个询问的答案之前，不会获得第 k+1个询问。

实际上，力扣平台上几乎所有的题目都是离线的，即一次性给出所有的询问。但在大部分情况下，我们按照下标顺序处理这些询问是没有问题的，也就是用在线的思维在离线的场景下解决问题。然而对于本题而言，我们必须按照一定的顺序处理 queries 中的询问，否则会使得时间复杂度没有保证。

思路与算法

我们将queries 按照 limit 从小到大进行排序，这样所有的询问中对边权的限制就单调递增了。

注意在给query排序的时候，可以另起一个数组qid,qid[i]=i,然后对这个数组进行排序，数组排序的比较函数是queris[i][2]<queris[j][2]。这样就可以保存queries中的id索引，索引按照queries的限制limit排序

同时，我们将edgeList 按照dis从小到大进行排序，这样所有的边权也就单调递增了。

使用并查集维护图的连通性，并且使用指针 count表示当前往并查集中添加的最后一条边。当我们处理到询问queriesj=(p,q,limit) 时，由于jlimits 是单调递增的，因此我们只需要往并查集中添加新的边，即不断地在 edgeList 中向右移动指针 count，直到当前指向的边权 >=limit为止。随后我们只需要使用并查集判断p和q是否连通即可。

在排序之后，我们依次遍历所有的元素。如果当前元素是 queries，我们就使用并查集进行查询（询问两个点是否连通）操作；如果当前元素是 edgeList，我们就是用并查集进行修改（添加一条边）操作。。

代码：

class UnionFind6{
public:
    vector<int>father;//父亲节点
    vector<int>rank;//秩的数
    int n;//节点个数
    int setCount;//连通分量数
public:
    //查询父结点
    UnionFind6(int _n):n(_n),setCount(_n),rank(_n,1),father(_n){
        //iota函数，令father[i]=i;
        iota(father.begin(),father.end(),0);
    }
    int find(int x){
        if(x==father[x])
            return x;
        else{
            father[x]=find(father[x]);
            return father[x];
        }
    }

    //并查集合并
    void merge(int i,int j){
        int x=find(i);
        int y=find(j);
        if(x!=y){
            if(rank[x]<=rank[y]){
                father[x]=y;
            }
            else{
                father[y]=x;
            }
            if(rank[x]==rank[y]&&x!=y)
                rank[y]++;
            setCount--;
        }
    }
    bool isConnected(int x,int y){
        x=find(x);
        y=find(y);
        return x==y;
    }
};
class Solution {
public:
    vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {
      vector<int>qid(queries.size());
      iota(qid.begin(),qid.end(),0);
      sort(qid.begin(),qid.end(),[&](int i,int j){
          return queries[i][2]<queries[j][2];
      });
      sort(edgeList.begin(),edgeList.end(),[](const vector<int>&e1, const vector<int>&e2){
          return e1[2]<e2[2];
      });
      //边按照边长排序，查询也按照边长限制排序
      int count=0;
      UnionFind6 unionFind6(n);
      vector<bool>ans(queries.size());
      for(int id:qid){
          while(count<edgeList.size()&&edgeList[count][2]<queries[id][2]){
              unionFind6.merge(edgeList[count][0],edgeList[count][1]);
              count++;
          }
          ans[id]=unionFind6.isConnected(queries[id][0],queries[id][1]);
      }
      return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

执行结果：

时间复杂度：O(mlogm+qlogq)，其中 m 和 qq分别是数组edgeList 和 queries 的长度。时间复杂度的瓶颈在于排序。

空间复杂度：O(n+logm+q)，其中 O(n) 为并查集，O(logm) 为数组 edgeList 排序使用的栈空间，O(q) 为存储所有询问的编号，对应排序中 O(logq) 的栈空间可以忽略。

52. 到达目的地第二短时间

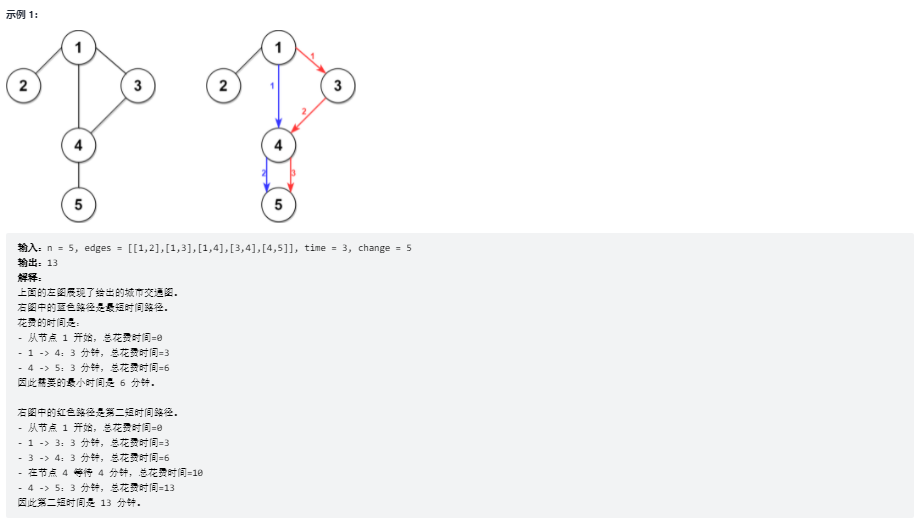
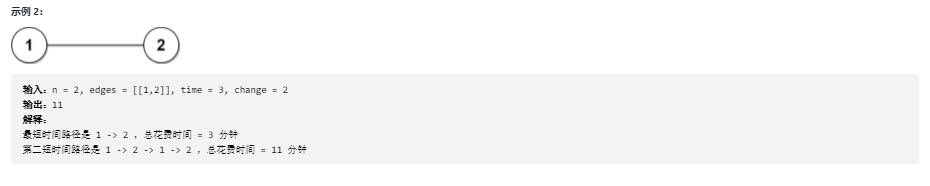
城市用一个 双向连通 图表示，图中有 n 个节点，从 1 到 n 编号（包含 1 和 n）。图中的边用一个二维整数数组 edges 表示，其中每个 edges[i] = [ui, vi] 表示一条节点 ui 和节点 vi 之间的双向连通边。每组节点对由 最多一条 边连通，顶点不存在连接到自身的边。穿过任意一条边的时间是 time 分钟。

每个节点都有一个交通信号灯，每 change 分钟改变一次，从绿色变成红色，再由红色变成绿色，循环往复。所有信号灯都 同时 改变。你可以在 任何时候 进入某个节点，但是 只能 在节点 信号灯是绿色时 才能离开。如果信号灯是 绿色 ，你 不能 在节点等待，必须离开。

第二小的值 是 严格大于 最小值的所有值中最小的值。

例如，[2, 3, 4] 中第二小的值是 3 ，而 [2, 2, 4] 中第二小的值是 4 。
给你 n、edges、time 和 change ，返回从节点 1 到节点 n 需要的 第二短时间 。

注意：

你可以 任意次 穿过任意顶点，包括 1 和 n 。
你可以假设在 启程时 ，所有信号灯刚刚变成 绿色 。

解法1：BFS按层次遍历

依题意知，同一路径长度所需要花费的时间是相同的（因为经过每条边所需要的时间相同），所以路径越长，所需时间越久。因此，如果我们可以求得到达目的地的严格次短路径，就可以直接计算到达目的地的第二短时间。

求解权重相同的最短路径问题可以采用广度优先搜索，这里我们做一些修改。使用广度优先搜索求解最短路径时，经过的点与初始点的路径长度是所有未搜索过的路径中的最小值，因此每次广度优先搜索获得的经过点与初始点的路径长度是非递减的。我们可以记录下所有点与初始点的最短路径与严格次短路径，一旦求得目的点的严格次短路径，我们就可以直接计算到达目的地的第二短时间。

算法思路：

平时我们都是求从某点出发，到某个点的最短距离或者时间，今天的题目则是让我们求第二短时间，但仔细想想，好像也和求最短时间没有太大的区别。

我们设置一个(n+1)*2的数组visit，dist[i][0]表示第一次到达第i个节点的最短时间，dist[i][1]表示第二次到达第i个节点的第二最短时间。

我们逐层遍历，设当前从队列中取出的节点为u，其连接的节点为v，当前花费的时间为step，移动花费的时间为time，则有：

如果step+time<dist[i][0]，则dist[i][0]不再是到达i的最短时间，而是第二短，故把dist[i][0]赋值给dist[i][1]，在用step+time更新dist[i][0]
如果step+time>dist[i][0] 且step+time<dist[i][1]，则dist[i][1]不再是到达i的第二短时间，直接用step+time更新dist[i][1]
在每层遍历结束后，我们需要更新step，每次遍历都需要+time。同时我们需要判断信号灯的颜色：

如果step/change为奇数，说明当前灯颜色为红灯，故需要等待，等待时间为 ((step/change)+1)*change-step
如果step/change为偶数，说明当前灯的颜色为绿灯，则可以继续走，不用等待。

代码：

class Solution {
public:
    int secondMinimum(int n, vector<vector<int>>& edges, int time, int change) {
        vector<vector<int>> graph(n + 1);
        for (auto &e : edges) {
            graph[e[0]].push_back(e[1]);
            graph[e[1]].push_back(e[0]);
        }
        queue<int>q;
        q.push(1);
        //dist[n][0]表示从1点到n点的最短距离
        //dist[n][1]表示1点到n的次短距离
        vector<vector<int>>dist(n+1,vector<int>(2,INT_MAX));
        dist[1][0]=0;
        int step=0; //step为到达第节点的时间，ti+1=step+twait+time
        while(dist[n][1]==INT_MAX){
            int len=q.size();
            for(int i=0;i<len;i++){
                int node=q.front();
                q.pop();
                for(int neigh:graph[node]){
                    if(step+time<dist[neigh][0]){
                        dist[neigh][1]=dist[neigh][0];
                        dist[neigh][0]=step+time;
                        q.push(neigh);
                    }
                    else if(step+time>dist[neigh][0]&&step+time<dist[neigh][1]){
                        dist[neigh][1]=step+time;
                        q.push(neigh);
                    }
                }
            }
            step+=time;
            int light=step/change;
            step+=(light%2==1)?(light+1)*change-step:0;
        }
        return dist[n][1];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

执行结果：

时间复杂度：O（n+m）n为节点数，m为边数

空间复杂度：O（n+m）n为节点数，m为边数

53.直方图的水量

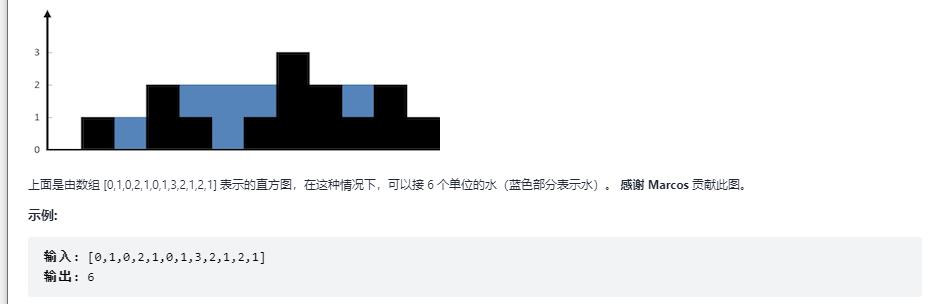
给定一个直方图(也称柱状图)，假设有人从上面源源不断地倒水，最后直方图能存多少水量?直方图的宽度为 1。

解法一：动态规划

按照列进行计算，可以看到第一列和最后一列肯定不能装水，那么中间的列可以装多少水，取决于它的左右两边。

求每一列的水，我们只需要关注当前列，以及左边最高的墙，右边最高的墙就够了。

装水的多少，当然根据木桶效应，我们只需要看左边最高的墙和右边最高的墙中较矮的一个就够了。

所以，根据较矮的那个墙和当前列的墙的高度可以分为三种情况。

1.较矮的墙的高度大于当前列的墙的高度。

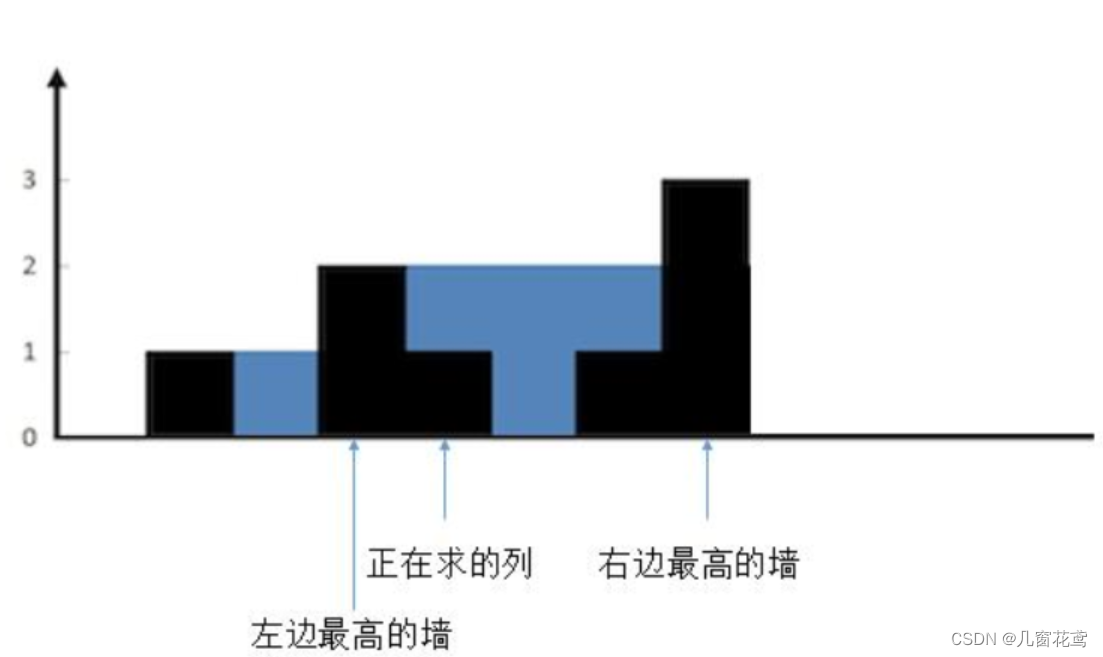
这样就很清楚了，现在想象一下，往两边最高的墙之间注水。正在求的列会有多少水？

很明显，较矮的一边，也就是左边的墙的高度，减去当前列的高度就可以了，也就是 2 - 1 = 1，可以存一个单位的水。

2.较矮的墙的高度小于当前列的墙的高度

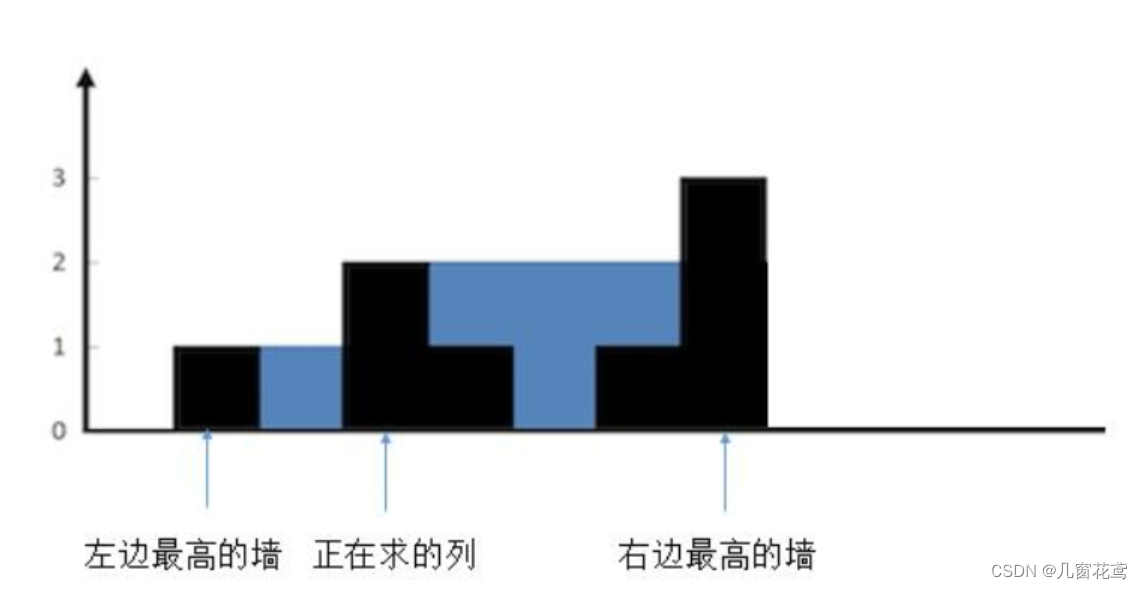
想象下，往两边最高的墙之间注水。正在求的列会有多少水？

正在求的列不会有水，因为它大于了两边较矮的墙。

3.较矮的墙的高度等于当前列的墙的高度

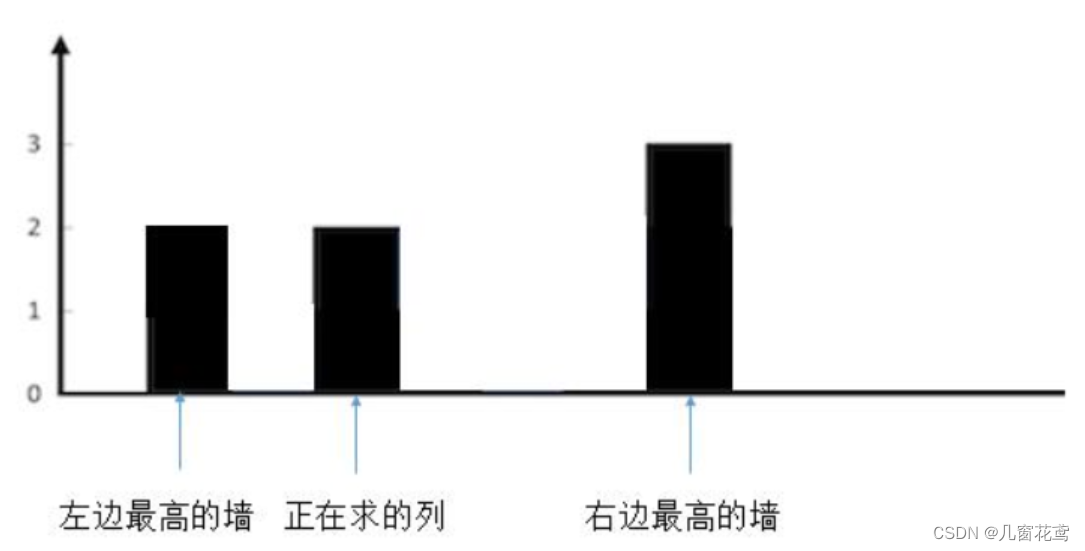
和第二种情况一样不会有水

因为求每列左边最高的墙和右边最高的墙的解法重复，其实可以使用动态规划的解法

maxLeft [i] 代表第 i 列左边最高的墙的高度，maxRight[i] 代表第 i 列右边最高的墙的高度。

maxLeft [i] = Max(maxLeft [i-1],height[i-1])。它前边的墙的左边的最高高度和它前边的墙的高度选一个较大的，就是当前列左边最高的墙了。

而maxRight[i] = Max(maxRight[i+1],height[i+1]) 。它后边的墙的右边的最高高度和它后边的墙的高度选一个较大的，就是当前列右边最高的墙了。

同时可以知道maxLeft[0]=0,和maxRight[height-1]=0,可以作为初始条件。

之后使用for循环找到每一列的maxLeft和maxRight的最小值与自己作比较，如果最小值比自己大，那么可以装水，否则不行。

同时需要注意，动态规划初始化时候maxLeft[0]和maxRight[n-1]都是0.

所以循环从1~n-2,但是由于n-2在for循环可能造成数组越界，所以开头判断如果n<2时，直接返回0.

代码：

class Solution {
public:
    int trap(vector<int>& height) {
         if(height.size()<2){
            return 0;
        }
        int res=0;
        int n=height.size();
        vector<int>maxLeft(n);
        vector<int>maxRight(n);
        maxLeft[0]=0;
        maxRight[n-2]=0;
        for(int i=1;i<=n-2;i++){
            maxLeft[i]=max(maxLeft[i-1],height[i-1]);
        }
        for(int j=n-2;j>=1;j--)
        {
            maxRight[j]=max(maxRight[j+1],height[j+1]);
        }
        for(int i=1;i<=n-2;i++){
            int m=min(maxLeft[i],maxRight[i]);
            if(m>height[i]){
                res+=(m-height[i]);
            }
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

执行结果：

时间复杂度：O(n)，其中 n 是数组 height 的长度。计算数组leftMax 和 rightMax 的元素值各需要遍历数组 height 一次，计算能接的水的总量还需要遍历一次。

空间复杂度：O(n)，其中 n 是数组 height 的长度。需要创建两个长度为 n 的数组leftMax 和 rightMax。

解法二：双指针

max_left = Math.max(max_left, height[i - 1]);

设置指针left=1;right=n-2;

height [ left - 1] 是可能成为 max_left 的变量， 同理，height [ right + 1 ] 是可能成为 right_max 的变量。

只要保证 height [ left - 1 ] < height [ right + 1 ] ，那么 max_left 就一定小于 max_right。

因为 max_left 是由 height [ left - 1] 更新过来的，而 height [ left - 1 ] 是小于 height [ right + 1] 的，而 height [ right + 1 ] 会更新 max_right，所以间接的得出 max_left 一定小于 max_right。

反之，我们就从右到左更。

代码：

class Solution {
public:
   int trap(vector<int>& height) {
        int sum=0;
        int n=height.size();
        int left=1;
        int right=n-2;
        int maxLeft=0;
        int maxRight=0;
        for(int i=1;i<=n-2;i++){
            //更新左指针
            if(height[left-1]<height[right+1]){
                maxLeft=max(maxLeft,height[left-1]);
                if(maxLeft>height[left])
                    sum+=maxLeft-height[left];
                left++;
            }
            //更新右指针
            else{
                maxRight=max(maxRight,height[right+1]);
                if(maxRight>height[right])
                    sum+=maxRight-height[right];
                right--;
            }
        }
        return sum;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

执行结果：

时间复杂度：O(n)，其中 n 是数组 height 的长度。计算数组leftMax 和 rightMax 的元素值各需要遍历数组 height 一次，计算能接的水的总量还需要遍历一次。

空间复杂度：O（1），使用双指针

54.T秒后青蛙的位置

给你一棵由 n 个顶点组成的无向树，顶点编号从 1 到 n。青蛙从 顶点 1 开始起跳。规则如下：

在一秒内，青蛙从它所在的当前顶点跳到另一个 未访问 过的顶点（如果它们直接相连）。
青蛙无法跳回已经访问过的顶点。
如果青蛙可以跳到多个不同顶点，那么它跳到其中任意一个顶点上的机率都相同。
如果青蛙不能跳到任何未访问过的顶点上，那么它每次跳跃都会停留在原地。
无向树的边用数组 edges 描述，其中 edges[i] = [fromi, toi] 意味着存在一条直接连通 fromi 和 toi 两个顶点的边。

返回青蛙在 t 秒后位于目标顶点 target 上的概率。

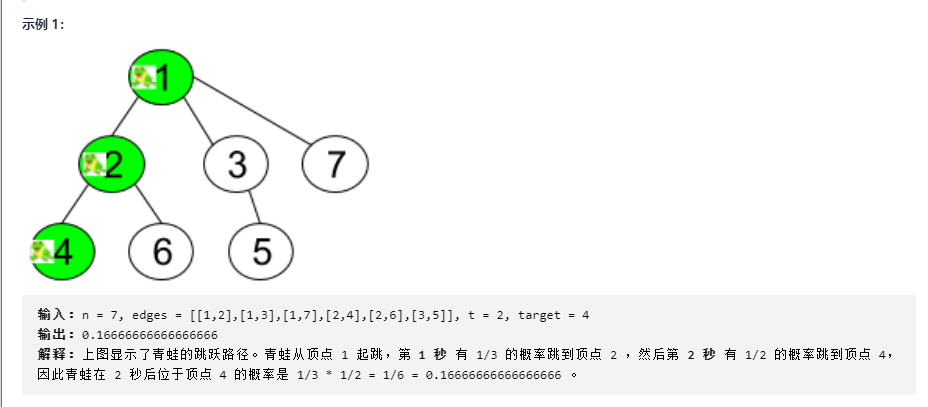
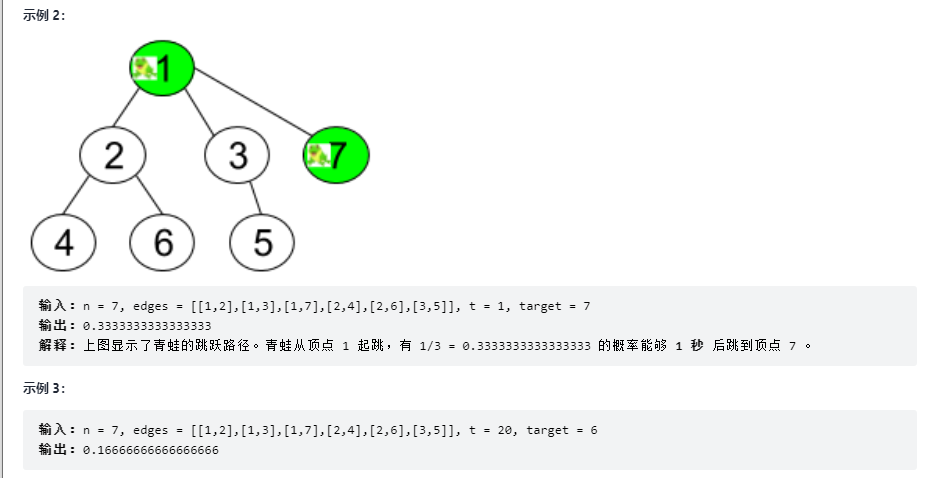
解法１：BFS宽度优先遍历

这是一道很容易想到用宽度优先遍历来解决的问题

其中需要关注几个问题

• 首先需要记录的是每个节点所在的层次，因为层次与给定的t设置有关系
• 每个节点需要去判断是否为叶子节点
• 同时因为是无向图，向下传递概率的时候需要考虑是否是1节点

进行bfs遍历，并记录每个节点的层次，概率，是否叶子节点的信息，因为青蛙不走回头路，需要用visited数组遍历记录是否访问过。

对于给定的target和t

• 如果target的层次比t大，那么肯定无法到达
• 如果target的层次比t小，并且target是叶子节点，那么可以到达,否则不行
• 如果target的层次与t相同时，可以到达

对于1节点，它的所有子节点的概率时起始节点的概率1与1/(连接的边数)的乘积

对于非1节点，它的概率传递时由起始节点的概率与与1/(连接的边数-1)的乘积

比如示例1中的2节点，连结3条边，其中有一条是父结点

55.互质树

给你一个 n 个节点的树（也就是一个无环连通无向图），节点编号从 0 到 n - 1 ，且恰好有 n - 1 条边，每个节点有一个值。树的 根节点 为 0 号点。

给你一个整数数组 nums 和一个二维数组 edges 来表示这棵树。nums[i] 表示第 i 个点的值，edges[j] = [uj, vj] 表示节点 uj 和节点 vj 在树中有一条边。

当 gcd(x, y) == 1 ，我们称两个数 x 和 y 是 互质的 ，其中 gcd(x, y) 是 x 和 y 的 最大公约数 。

从节点 i 到 根 最短路径上的点都是节点 i 的祖先节点。一个节点 不是 它自己的祖先节点。

请你返回一个大小为 n 的数组 ans ，其中 ans[i]是离节点 i 最近的祖先节点且满足 nums[i] 和 nums[ans[i]] 是 互质的 ，如果不存在这样的祖先节点，ans[i] 为 -1 。

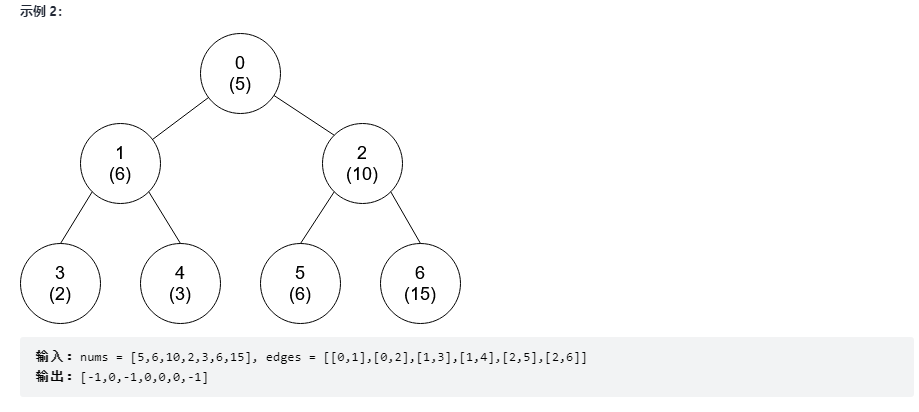
解法：DFS 记录所有最近的互质节点

切入点和解题思路
如果用蛮力检查一个节点的所有的祖先节点，那么，一个节点的祖先节点最多能有 n−1 个，显然会超时的。
一个重要的切入点是： nums[i]≤50。我们不妨换一种思路：从节点的值 x 出发，枚举满足 1≤y≤50 且 gcd(x,y)=1 的 y，并对每个 y 找出离着节点 i 最近的点，最后再在这些点中求出离着当前点最近的点即可。这样只需检查 50 次即可。
那么，如何对于任一数字 y，找出离当前节点 i 最近的祖先节点呢？首先可以想到的是，离着节点 i 最近的满足条件的祖先节点，也是这些点中 最深 的。我们不妨对每个数字 1∼50 维护一个栈，并采用 dfs 的思路。每当我们要遍历下一个节点时，就把当前节点的编号 （node）和节点的深度（level）push 到 当前节点的值 （x） 对应的栈中。这样，栈顶就是数字 x 的、最深 的节点，也是我们之后需要的关于数字x 的 最近 的节点。此外，要记得 dfs 完成后要将之前 push 进去的元素 pop 出来。（回溯）

总结：

对每个数字 1∼50 维护一个栈，向下dfs过程中栈顶就是数字 x 的层数最深的节点，也即当前结点的最近父代结点，各个候选人全在栈顶
dfs 回溯阶段栈顶元素需要出栈

代码：

class Solution {
public:
    vector<vector<int>> G;
    stack<pair<int,int>> lasts[55];
    vector<int> res;
    void dfs(int node, int pre, int level, vector<int>& a) {
        int re = -1, lev = -1;
        for(int i = 1; i <= 50; ++i) {
            if(lasts[i].size() && lasts[i].top().first > lev && __gcd(i, a[node]) == 1) {
                re = lasts[i].top().second;
                lev = lasts[i].top().first;
            }
        }
        res[node] = re;
        for(int ne : G[node]) {
            if(ne != pre) {
                lasts[a[node]].push({level, node});
                dfs(ne, node, level + 1, a);
                lasts[a[node]].pop();
            }
        }
    }
    vector<int> getCoprimes(vector<int>& nums, vector<vector<int>>& edges) {
        int n = nums.size();
        G.resize(n);
        for(auto& e : edges) {
            G[e[0]].push_back(e[1]);
            G[e[1]].push_back(e[0]);
        }
        res.resize(n);
        dfs(0, -1, 0, nums);
        return res;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

执行结果：

时间复杂度：O（n+m）

空间复杂度：O（n）

56.花括号展开

如果你熟悉 Shell 编程，那么一定了解过花括号展开，它可以用来生成任意字符串。

花括号展开的表达式可以看作一个由 花括号、逗号 和 小写英文字母 组成的字符串，定义下面几条语法规则：

如果只给出单一的元素 x，那么表达式表示的字符串就只有 “x”。R(x) = {x}
例如，表达式 “a” 表示字符串 “a”。
而表达式 “w” 就表示字符串 “w”。
当两个或多个表达式并列，以逗号分隔，我们取这些表达式中元素的并集。R({e_1,e_2,…}) = R(e_1) ∪ R(e_2) ∪ …
例如，表达式 “{a,b,c}” 表示字符串 “a”,“b”,“c”。
而表达式 “{{a,b},{b,c}}” 也可以表示字符串 “a”,“b”,“c”。
要是两个或多个表达式相接，中间没有隔开时，我们从这些表达式中各取一个元素依次连接形成字符串。R(e_1 + e_2) = {a + b for (a, b) in R(e_1) × R(e_2)}
例如，表达式 “{a,b}{c,d}” 表示字符串 “ac”,“ad”,“bc”,“bd”。
表达式之间允许嵌套，单一元素与表达式的连接也是允许的。
例如，表达式 “a{b,c,d}” 表示字符串 “ab”,“ac”,“ad”。
例如，表达式 “a{b,c}{d,e}f{g,h}” 可以表示字符串 “abdfg”, “abdfh”, “abefg”, “abefh”, “acdfg”, “acdfh”, “acefg”, “acefh”。
给出表示基于给定语法规则的表达式 expression，返回它所表示的所有字符串组成的有序列表。

假如你希望以「集合」的概念了解此题，也可以通过点击 “显示英文描述” 获取详情。

解法1：BFS广度优先遍历树

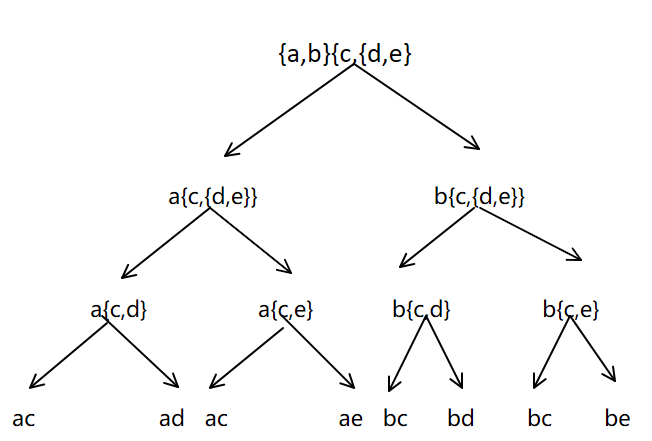
如果所示，上述题目可以分解成一个广度优先遍历树的形式

所以可以从左到右，从里到外去遍历寻找“{”和“}”作为切割的关键

将字符串切割成三个部分，“{”左边，“}”右边，以及“{”“}”中间以“，”分割

之后将左边，右边和中间分割后的string数组中的每一个拼接后入队

之后在重复上述操作，直到没有括号，将结果加入结果集

注意结果集需要用set来去重

代码：

class Solution {
public:    
  vector<string> braceExpansionII(string expression)
    {
        unordered_set<string>res;
        queue<string>que;
        que.push(expression);
        while(!que.empty()){
            string str=que.front();
            que.pop();
            if(str.find("{")==string::npos){
                res.insert(str);
                continue;
            }
            int i=0;
            int left=0;
            int right=0;
            while(str[i]!='}'){
                if(str[i]=='{')
                    left=i;
                i++;
            }
            right=i;
            string leftStr=str.substr(0,left);
            string midStr=str.substr(left+1,right-left-1);
            string rightStr="";
            if(right+1<str.size())
               rightStr=str.substr(right+1);
            vector<string>mid=split(midStr,',');
            for(string &m:mid){
                que.push(leftStr+m+rightStr);
            }
        }
        vector<string>ans(res.begin(),res.end());
        sort(ans.begin(),ans.end());
        return ans;
    }


    //因为c++没有split函数，所以需要自己编写一个split
    vector<string> split(string s, char x)
    {
        int n = s.size();
        vector<string> res;
        int L = 0;
        int R = 0;
        while (R < n)
        {
            if (s[R] != x)
                R ++;
            else
            {
                res.push_back(s.substr(L, R - L));
                L = R + 1;
                R = L;
            }
        }
        if (L < R)
            res.push_back(s.substr(L, R - L));
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

执行结果：

时间复杂度：O（n^2）

空间复杂度：O（n）

57.规定时间内到达终点的最小花费

一个国家有 n 个城市，城市编号为 0 到 n - 1 ，题目保证 所有城市 都由双向道路 连接在一起 。道路由二维整数数组 edges 表示，其中 edges[i] = [xi, yi, timei] 表示城市 xi 和 yi 之间有一条双向道路，耗费时间为 timei 分钟。两个城市之间可能会有多条耗费时间不同的道路，但是不会有道路两头连接着同一座城市。

每次经过一个城市时，你需要付通行费。通行费用一个长度为 n 且下标从 0 开始的整数数组 passingFees 表示，其中 passingFees[j] 是你经过城市 j 需要支付的费用。

一开始，你在城市 0 ，你想要在 maxTime 分钟以内 （包含 maxTime 分钟）到达城市 n - 1 。旅行的 费用 为你经过的所有城市 通行费之和 （包括 起点和终点城市的通行费）。

给你 maxTime，edges 和 passingFees ，请你返回完成旅行的 最小费用 ，如果无法在 maxTime 分钟以内完成旅行，请你返回 -1 。

解法：动态规划

这是一道很明显的动态规划题目，首先抓住会转变的变量：花费时间t,以及城市。

对于路径并没有要求最短路径，只要在不超过maxTime的路径即可。

定义二维数组dp[t][i]

我们用dp[t][i] 表示使用恰好 t 分钟到达城市 i 需要的最少通行费总和。

在状态转移时，我们考虑最后一次通行是从城市 j 到达城市 i 的，那么有状态转移方程：

$$dp[t][i]=mi{n}_{(j,i)\in E}(dp[t-cost(j,i)][j]+passingFees[i],dp[t][i])$$
cost(j,i)为这两个城市连接花费的费用

初始状态``dp[0][0]=passingFees[0]` 一开始0分钟通过0号城市的费用为passingFees[0]

由于我们的状态转移方程中的目标的最小值，因此对于其它的状态，我们可以在一开始赋予它们一个极大∞。如果最终的答案为∞，说明无法在 maxTime 及以内完成旅行，返回 −1。

此外，本题中的道路是以数组 edges 的形式给定的，在动态规划的过程中，如果我们使用两重循环枚举 t 和 i，就不能利用 edges，而需要使用额外的数据结构存储以 i 为端点的所有道路。一种合理的解决方法是，我们使用一重循环枚举 t，另一重循环枚举 edges 中的每一条边 (i,j,cost)，通过这条边更新dp[t][i]以及dp[t][i]的值。

58.重新安排行程

给你一份航线列表 tickets ，其中 tickets[i] = [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。

所有这些机票都属于一个从 JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。

例如，行程 [“JFK”, “LGA”] 与 [“JFK”, “LGB”] 相比就更小，排序更靠前。
假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次。

解法：DFS深度优先遍历+贪心+优先队列

我们化简本题题意：给定一个 nn 个点 mm 条边的图，要求从指定的顶点出发，经过所有的边恰好一次（可以理解为给定起点的「一笔画」问题），使得路径的字典序最小。

这种「一笔画」问题与欧拉图或者半欧拉图有着紧密的联系，下面给出定义：

通过图中所有边恰好一次且行遍所有顶点的通路称为欧拉通路。

通过图中所有边恰好一次且行遍所有顶点的回路称为欧拉回路。

具有欧拉回路的无向图称为欧拉图。

具有欧拉通路但不具有欧拉回路的无向图称为半欧拉图。

因为本题保证至少存在一种合理的路径，也就告诉了我们，这张图是一个欧拉图或者半欧拉图。我们只需要输出这条欧拉通路的路径即可。

欧拉通路和欧拉图：

如果没有保证至少存在一种合理的路径，我们需要判别这张图是否是欧拉图或者半欧拉图，具体地：

对于无向图 G，G 是欧拉图当且仅当 G 是连通的且没有奇度顶点。

对于无向图 G，G 是半欧拉图当且仅当 G 是连通的且 G 中恰有 2 个奇度顶点。

对于有向图 G，G 是欧拉图当且仅当 G 的所有顶点属于同一个强连通分量且每个顶点的入度和出度相同。

对于有向图 G，G是半欧拉图当且仅当 G 的所有顶点属于同一个强连通分量且

恰有一个顶点的出度与入度差为 1；

恰有一个顶点的入度与出度差为 1；

所有其他顶点的入度和出度相同。

让我们考虑下面的这张图：

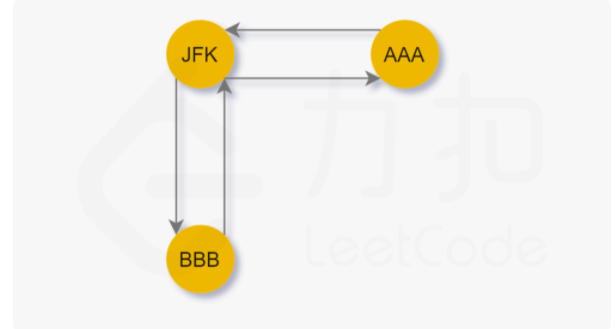
我们从起点 \text{JFK}JFK 出发，合法路径有两条：

JFK→AAA→JFK→BBB→JFK

JFK→BBB→JFK→AAA→JFK

既然要求字典序最小，那么我们每次应该贪心地选择当前节点所连的节点中字典序最小的那一个，并将其入栈。最后栈中就保存了我们遍历的顺序。

为了保证我们能够快速找到当前节点所连的节点中字典序最小的那一个，我们可以使用优先队列存储当前节点所连到的点，每次我们 O(1) 地找到最小字典序的节点，并 O(logm) 地删除它。

然后我们考虑一种特殊情况：

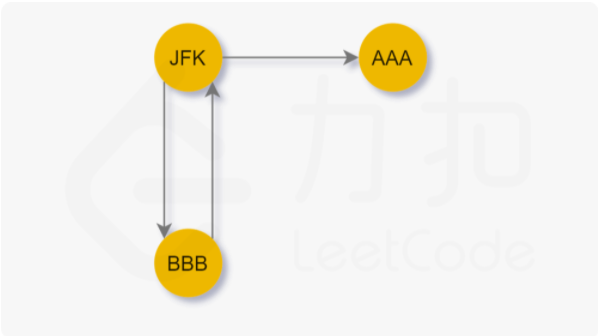
当我们先访AAA 时，我们无法回到 JFK，这样我们就无法访问剩余的边了。

也就是说，当我们贪心地选择字典序最小的节点前进时，我们可能先走入「死胡同」，从而导致无法遍历到其他还未访问的边。于是我们希望能够遍历完当前节点所连接的其他节点后再进入「死胡同」。

注意对于每一个节点，它只有最多一个「死胡同」分支。依据前言中对于半欧拉图的描述，只有那个入度与出度差为 1 的节点会导致死胡同。

方法一：Hierholzer 算法
思路及算法

Hierholzer 算法用于在连通图中寻找欧拉路径，其流程如下：

从起点出发，进行深度优先搜索。

每次沿着某条边从某个顶点移动到另外一个顶点的时候，都需要删除这条边。

如果没有可移动的路径，则将所在节点加入到栈中，并返回。

当我们顺序地考虑该问题时，我们也许很难解决该问题，因为我们无法判断当前节点的哪一个分支是「死胡同」分支。

不妨倒过来思考。我们注意到只有那个入度与出度差为 1 的节点会导致死胡同。而该节点必然是最后一个遍历到的节点。我们可以改变入栈的规则，当我们遍历完一个节点所连的所有节点后，我们才将该节点入栈（即逆序入栈）。[下面代码中使用了vector结构，并在头部插入，最后可以直接返回结果，不用逆序]

对于当前节点而言，从它的每一个非「死胡同」分支出发进行深度优先搜索，都将会搜回到当前节点。而从它的「死胡同」分支出发进行深度优先搜索将不会搜回到当前节点。也就是说当前节点的死胡同分支将会优先于其他非「死胡同」分支入栈。

这样就能保证我们可以「一笔画」地走完所有边，返回结果。

代码：

class Solution {
public:
    unordered_map<string,priority_queue<string,vector<string>,greater<string>>>graph;
    vector<string>res;//用栈保存
    vector<string> findItinerary(vector<vector<string>>& tickets) {
        for(auto &t:tickets){
            graph[t[0]].emplace(t[1]);
        }
        dfs("JFK");
        return res;
    }
    void dfs(const string & c){
        while(graph.count(c)&&graph[c].size()>0){
            string tmp=graph[c].top();
            graph[c].pop();
            dfs(tmp);
        }
        res.insert(res.begin(),c);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

执行结果：

时间复杂度：O(mlogm)，其中 mm 是边的数量。对于每一条边我们需要 O(logm) 地删除它，最终的答案序列长度为 m+1，而与 n 无关。

空间复杂度：O(m)，其中 m 是边的数量。我们需要存储每一条边。

59.解出数学表达式的学生分数

给你一个字符串 s ，它 只 包含数字 0-9 ，加法运算符 ‘+’ 和乘法运算符 ‘*’ ，这个字符串表示一个 合法 的只含有 个位数数字 的数学表达式（比方说3+5*2）。有 n 位小学生将计算这个数学表达式，并遵循如下 运算顺序 ：

按照 从左到右 的顺序计算 乘法 ，然后
按照 从左到右 的顺序计算 加法 。
给你一个长度为 n 的整数数组 answers ，表示每位学生提交的答案。你的任务是给 answer 数组按照如下 规则 打分：

如果一位学生的答案 等于 表达式的正确结果，这位学生将得到 5 分。
否则，如果答案由 一处或多处错误的运算顺序 计算得到，那么这位学生能得到 2 分。
否则，这位学生将得到 0 分。
请你返回所有学生的分数和。

解法一：DFS递归+记忆化搜索

利用递归的操作计算出所有的可能的错误计算结果，其中必须使用记忆化搜索，否则可能超时。

例如“7+3*2”

从第一个符号“+”开始，递归得到+左右两边的错误值的集合（用set 因为可能有重复）

递归的出口为当递归的字符串只有一个数字时，递归的结果集中加入这个数组，可以直接返回。

递归的过程：

移动符号，得到符号左边的算式结果集和符号右边的算式的结果集

两个结果集的所有结果根据这个符号做“+"或者”*“。

最后使用map记忆化的记录中间过程，返回结果集。

注意条件 计算的结果在0-1000，那么可以在这里进行剪枝，因为+和乘法只会使得数字越来越大，所以只有递归结果<1000，才加入错误结果集

代码：

class Solution {
public:
    unordered_map<string ,unordered_set<int>>map;
    int scoreOfStudents(string s, vector<int>& answers) {
        unordered_set<int>errRes=getErrRes(s);
        int right=getRight(s);
        auto it=errRes.erase(right);
        int ans=0;
        for(int i=0;i<answers.size();i++){
            int a=answers[i];
            if(a==right)
                ans+=5;
            else if(errRes.count(a))
                ans+=2;
        }
        return ans;
    }
    int getRight(string &s){
        stack<int>stack;
        stack.push(s[0]-'0');
        for(int i=1;i<s.length();i+=2){
            if(s[i]=='+'){
                stack.push(s[i+1]-'0');
            }
            else{
                stack.top()*=(s[i+1]-'0');
            }
        }
        int sum=0;
        while(!stack.empty()){
            sum+=stack.top();
            stack.pop();
        }
        return sum;
    }
    unordered_set<int> getErrRes(const string &s){
        unordered_set<int>errres;
        if(s.length()==1)
            errres.insert(s[0]-'0');
        if(map.count(s)){
            return map[s];
        }
        for(int i=1;i<s.length();i+=2){
            char ch =s[i];
            unordered_set<int>leftSet=getErrRes(s.substr(0,i-0));
            unordered_set<int>rightSet=getErrRes(s.substr(i+1));
            for(int left:leftSet)
                for(int right:rightSet){
                    int val=(ch=='*'?(left*right):left+right);
                    if(val<=1000)
                        errres.insert(val);
                }
        }
        map[s]=errres;
        return errres;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

执行结果：

时间复杂度：O（n^4）

空间复杂度：O（n）

解法二：动态规划

既然可以使用dfs+记忆化搜索，那么自然可以使用动态规划求解

这个题难点在于对运算顺序自由组合时，不知道怎么做组合。
其实可以简单的把一个表达式，拆分成

总表达式 = (左侧表达式) 运算符 (右侧表达式)

的形式，先计算左侧表达式所有可能结果，再计算右侧表达式所有可能结果，再两两组合得到总表达式的所有结果。

具体操作时，对于一个总表达式，枚举它内部所有的运算符位置，然后每次计算左和右。可以观察到，左和右表达式显然长度≤总表达式长度，不难想到应该用 dp来解。

具体代码时，使用区间 dp 的方法，使用一个二维数组dp[i][j] 表示字符串 s[i…j]总共可以通过调换计算顺序，得到哪些计算结果。

如此一来，假设我们知道了两个区间结果 dp[i][k]和 dp[k][j]，那我们就可以通过

来一步步从小区间扩大到大区间。

代码：

class Solution {
public:    
    int scoreOfStudents(string s, vector<int>& answers) {
        int len = s.length();
        //统计学生答案
        vector<int> count(1001);
        for (int p:answers)
            count[p]++;
        //计算正确结果
        stack<int> stack;
        stack.push(s[0] - '0');
        for (int i = 1; i < s.length(); i += 2) {
            if (s[i] == '+') {
                stack.push(s[i + 1] - '0');
            } else {
                stack.top() *= (s[i + 1] - '0');
            }
        }
        int sum = 0;
        while (!stack.empty()) {
            sum += stack.top();
            stack.pop();
        }
        //计算正确结果的得分
        int ans = 5 * count[sum];
        vector<vector<unordered_set<int>>> dp(len, vector<unordered_set<int>>(len));
        //枚举其他所有的可能结果 dp[i][j]表示字符串s[i,j]的所有可能结果
        for (int j = 0; j < len; j += 2) {
            dp[j][j].insert(s[j] - '0');
        }//相当于dfs的递归出口
        for (int step = 2; step < len; step += 2) {
            //枚举左半部分的开始位置i
            for (int i = 0; i + step < len; i += 2) {
                //枚举左半部分的长度t
                for (int t = 0; t < step; t += 2) {
                    //x是左半部分的所有可能值
                    //y是右半部分的所有可能值
                    for (auto x:dp[i][i + t]) {
                        for (auto y:dp[i + t + 2][i + step]) {
                            //根据左半部分和右半部分的中间连接符来计算后的值
                            int tmp = s[i + t + 1] == '+' ? x + y : x * y;
                            if (tmp <= 1000)
                                dp[i][i + step].insert(tmp);
                        }
                    }
                }
            }
        }
        //统计错误同学得分
        for(int p:dp[0][len-1]){
            if(p!=sum){
                ans+=2*count[p];
            }
        }
        return ans;
    }

};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

执行结果：

时间复杂度：O（n^3）

空间复杂度：O（n^2）

60.树节点的第K个祖先

给你一棵树，树上有 n 个节点，按从 0 到 n-1 编号。树以父节点数组的形式给出，其中 parent[i] 是节点 i 的父节点。树的根节点是编号为 0 的节点。

请你设计并实现 getKthAncestor(int node, int k) 函数，函数返回节点 node 的第 k 个祖先节点。如果不存在这样的祖先节点，返回 -1 。

树节点的第 k 个祖先节点是从该节点到根节点路径上的第 k 个节点。

解法：动态规划

Binary Lifting 的本质其实是 dp。dp[node][j] 存储的是 node 节点距离为 2^j 的祖先是谁。

根据定义，dp[node][0] 就是 parent[node]，即 node 的距离为 1 的祖先是 parent[node]。

状态转移方程是：dp[node][j] = dp[dp[node][j - 1]][j - 1]。

意思是：要想找到 node 的距离 2^j 的祖先，先找到 node 的距离 2^(j - 1) 的祖先，然后，再找这个祖先的距离 2^(j - 1) 的祖先。两步得到 node 的距离为 2^j 的祖先。

这样可能有点绕，举个例子：

例如dp[3][1]是要找节点三的第2个祖先，dp[3][1]=dp[dp[3][0]][0] 它就等于找3的第一个祖先的第一个祖先，就是节点3的第二个祖先了。

所以，我们要找到每一个 node 的距离为 1, 2, 4, 8, 16, 32, … 的祖先，直到达到树的最大的高度。树的最大的高度是 logn 级别的。

这样做，状态总数是 O(nlogn)，可以使用 O(nlogn) 的时间做预处理。

之后，根据预处理的结果，可以在 O(logn) 的时间里完成每次查询：对于每一个查询 k，把 k 拆解成二进制表示，然后根据二进制表示中 1 的位置，累计向上查询。

代码：

   class TreeAncestor {
        vector<vector<int>>dp;
    public:
        //预处理
        TreeAncestor(int n, vector<int>& parent) {
            int m=0;
            for(int i=1;i<=n;i*=2){
                m++;
            }
            dp.assign(n,vector<int>(m,-1));
            for(int i=0;i<n;i++){
                dp[i][0]=parent[i];
            }
            for(int i=0;i<n;i++)
                for(int j=1;j<m;j++){
                    if(dp[i][j-1]==-1){ //有可能节点i没有第2^{j-1}个祖先节点
                        continue;
                    }
                    dp[i][j]=dp[dp[i][j-1]][j-1];
                }
        }

        int getKthAncestor(int node, int k) {
            //因为k的最大为5*10^4,2^16=65535 所以只要最多16位二进制就能表示
            for(int i=0;i<16;i++){
                if(k&(1<<i))node=dp[node][i];
                if(node==-1)break;
            }
            return node;
        }
    };
/**
 * Your TreeAncestor object will be instantiated and called as such:
 * TreeAncestor* obj = new TreeAncestor(n, parent);
 * int param_1 = obj->getKthAncestor(node,k);
 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

执行结果：

时间复杂度：O（nlogn)

空间复杂度：O（1）

61.全部开花最早的一天

你有 n 枚花的种子。每枚种子必须先种下，才能开始生长、开花。播种需要时间，种子的生长也是如此。给你两个下标从 0 开始的整数数组 plantTime 和 growTime ，每个数组的长度都是 n ：

plantTime[i] 是 播种 第 i 枚种子所需的 完整天数 。每天，你只能为播种某一枚种子而劳作。无须 连续几天都在种同一枚种子，但是种子播种必须在你工作的天数达到 plantTime[i] 之后才算完成。
growTime[i] 是第 i 枚种子完全种下后生长所需的 完整天数 。在它生长的最后一天 之后 ，将会开花并且永远 绽放 。
从第 0 开始，你可以按 任意 顺序播种种子。

返回所有种子都开花的 最早 一天是第几天。

解法：贪心算法

很容易想到，最好让生长期长的种子先播种，可以尽量在其他花生长的期间去播种更多种子。

贪心策略证明：

代码：

class Solution {
public:
    int earliestFullBloom(vector<int>& plantTime, vector<int>& growTime) {
        vector<int>order(plantTime.size());
        iota(order.begin(),order.end(),0);
        //使用lambd自定义排序行排序
        //捕获外部作用域中所有变量，并作为引用在函数体中使用（按引用捕获）
        sort(order.begin(),order.end(),[&](int i,int j){
            return growTime[i]>growTime[j];
        });
        int ans=0;
        int endtime=0;
        for(int i:order){
            endtime+=plantTime[i];
            ans=max(ans,endtime+growTime[i]);
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

执行结果：

时间复杂度：O（nlogn）

空间复杂度：O(n)

62. 合并多棵二叉搜索树

给你 n 个 二叉搜索树的根节点 ，存储在数组 trees 中（下标从 0 开始），对应 n 棵不同的二叉搜索树。trees 中的每棵二叉搜索树 最多有 3 个节点 ，且不存在值相同的两个根节点。在一步操作中，将会完成下述步骤：

选择两个 不同的 下标 i 和 j ，要求满足在 trees[i] 中的某个 叶节点 的值等于 trees[j] 的 根节点的值 。
用 trees[j] 替换 trees[i] 中的那个叶节点。
从 trees 中移除 trees[j] 。
如果在执行 n - 1 次操作后，能形成一棵有效的二叉搜索树，则返回结果二叉树的 根节点 ；如果无法构造一棵有效的二叉搜索树，返回 null 。

二叉搜索树是一种二叉树，且树中每个节点均满足下述属性：

任意节点的左子树中的值都 严格小于 此节点的值。
任意节点的右子树中的值都 严格大于 此节点的值。
叶节点是不含子节点的节点。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KPjaRn95-1651404758969)(C:\Users\gcc\AppData\Roaming\Typora\typora-user-images\image-20220217235434191.png)]

解法：DFS递归遍历+哈希表

合成一棵树的前提条件
条件一：叶子节点的值不能重复。

不难发现，合并操作只会删掉根节点，无法删除其他位置的节点。

因此如果叶子节点有重复，必然无法构造出二叉搜索树。

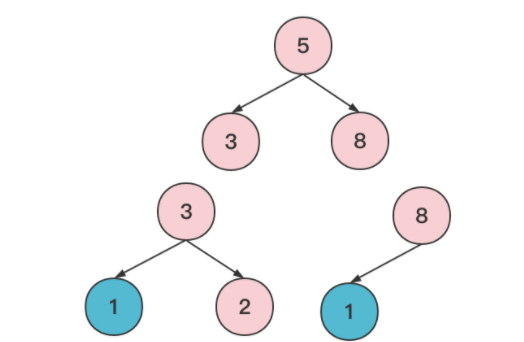
条件二：设 S 为叶子节点的值的集合，则有且仅有一个根节点的值不在 S 内。

当有多个根节点的值不在 S 内时，意味着有多棵树无法合并到其他树的叶子节点，则必然无法合成一棵树。

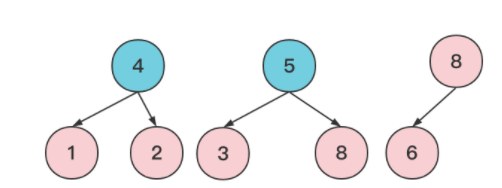
当所有根节点的值都在 S 内时，意味着有出现了合并的回路，类似于下图：

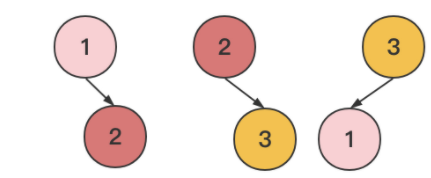
假设输入数据符合上述条件，不妨设值不在 SS 中的根节点为 final_rootfinal_root。

为了方便实现合并操作，维护一个根节点的值到根节点的映射关系：

接下来，开始遍历 final_root 代表的树:

每遇到一个叶子节点 leaf，就从 dict中取出对应的根节点 root
并将 root 合并到 leaf，并从 dict 中删除 root
继续遍历 leaf 的左右子节点
从 dict 中删除 root 是为了避免局面合并回路导致死循环，比如：

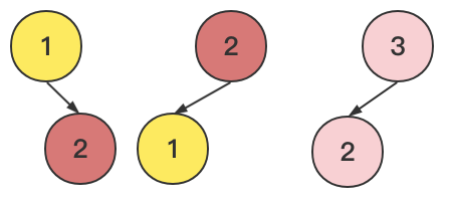
如果不删除，则遍历会陷入 3->2->1->2->1->... 的死循环。

最后，需要再做一次中序遍历，如果中序遍历是升序，则为二叉搜索树，否则不是。

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<int,TreeNode*>root;
    TreeNode* canMerge(vector<TreeNode*>& trees) {
        //首先如果叶子节点重复，不能构造二叉搜索树
        //而且必须只有一棵树的根节点不在叶子节点的集合中
        unordered_set<int>leaves;
        //检查叶子节点是否重复
        for(auto t:trees){
            //set的insert方法返回pair<迭代器，是否插入成功bool>
            //如果返回的bool值为false，说明叶子节点已经存在了，叶子节点重复
            //肯定没办法形成二叉搜索树，直接返回false
            if(t->left!=nullptr){
               if( leaves.insert(t->left->val).second== false)
                   return nullptr;
            }
            if(t->right!= nullptr){
                if( leaves.insert(t->right->val).second== false)
                    return nullptr;
            }
        }
        //检查是否只有一棵树的根节点不在叶子节点的集合中
        int count=0;
        TreeNode * binaryRoot;
        for(auto t:trees){
            if(leaves.count(t->val)){
                count++;
            }
            else{
                binaryRoot=t;
            }
        }
        if(count+1!=trees.size())
            return nullptr;
        //构造根节点的集合
        for(auto t:trees){
            if(t!=binaryRoot){
                root[t->val]=t;
            }
        }
        dfs(binaryRoot);
        if(!root.empty())
            return nullptr;
        vector<int>arr;
        midorder(binaryRoot,arr);
        if(isValid(arr))
            return binaryRoot;
        else
            return nullptr;

    }
   void dfs(TreeNode* node){
        if(node== nullptr){
            return ;
        }
        if(node->left== nullptr&&node->right==nullptr){
            auto it=root.find(node->val);
            if(it!=root.end()){
                node->left=root[node->val]->left;
                node->right=root[node->val]->right;
                root.erase(node->val);
            }
        }
        dfs(node->left);
        dfs(node->right);
    }
   void midorder(TreeNode *root,vector<int>&arr){
        if(root){
            midorder(root->left,arr);
            arr.push_back(root->val);
            midorder(root->right,arr);
        }
    }
    bool isValid(vector<int>arr){
        int n=arr.size();
        for(int i=0;i<n-1;i++){
            if(arr[i]>arr[i+1])
                return false;
        }
        return true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93

执行结果：

时间复杂度：O（n）

空间复杂度：O（n）