devbox
IT小白
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

Pytorch：RNN、LSTM、GRU、Bi-GRU、Bi-LSTM、梯度消失、梯度爆炸

作者：IT小白 | 2024-04-06 17:19:43

赞

踩

bi-gru

日萌社

人工智能AI：Keras PyTorch MXNet TensorFlow PaddlePaddle 深度学习实战（不定时更新）

1. RNN架构解析

1.1 认识RNN模型

  • 学习目标:
    • 了解什么是RNN模型.
    • 了解RNN模型的作用.
    • 了解RNN模型的分类.

  • 什么是RNN模型:

    • RNN(Recurrent Neural Network), 中文称作循环神经网络, 它一般以序列数据为输入, 通过网络内部的结构设计有效捕捉序列之间的关系特征, 一般也是以序列形式进行输出 
  • 一般单层神经网络结构:

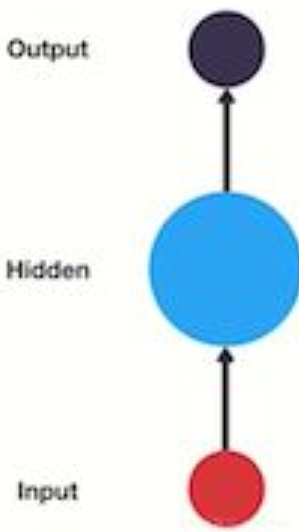
  • RNN单层网络结构:

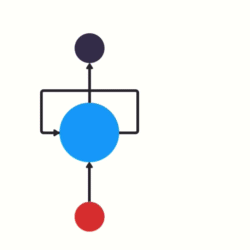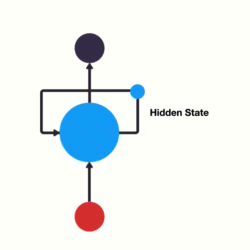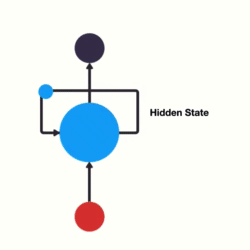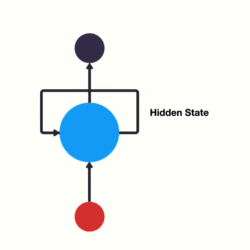
  • 以时间步对RNN进行展开后的单层网络结构:


  • RNN的循环机制使模型隐层上一时间步产生的结果, 能够作为当下时间步输入的一部分(当下时间步的输入除了正常的输入外还包括上一步的隐层输出)对当下时间步的输出产生影响.
  • RNN模型的作用:
    • 因为RNN结构能够很好利用序列之间的关系, 因此针对自然界具有连续性的输入序列, 如人类的语言, 语音等进行很好的处理, 广泛应用于NLP领域的各项任务, 如文本分类, 情感分析, 意图识别, 机器翻译等.
  • 下面我们将以一个用户意图识别的例子进行简单的分析:

  • 第一步: 用户输入了"What time is it ?", 我们首先需要对它进行基本的分词, 因为RNN是按照顺序工作的, 每次只接收一个单词进行处理.

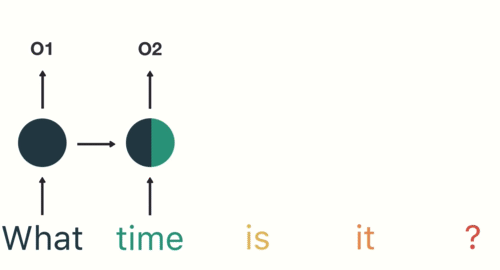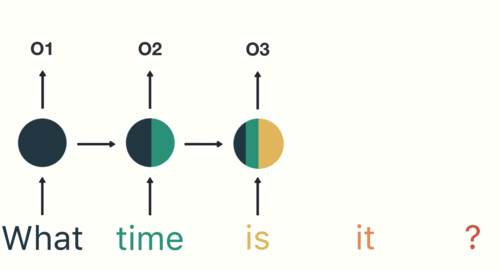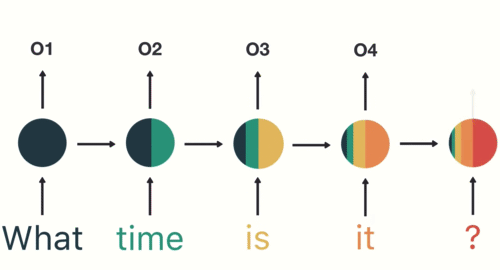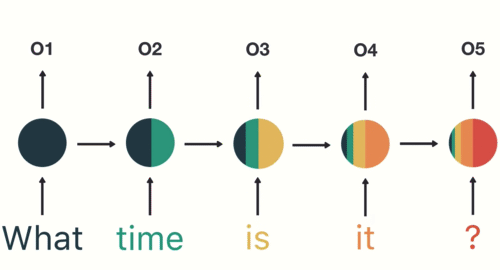
  • 第二步: 首先将单词"What"输送给RNN, 它将产生一个输出O1.


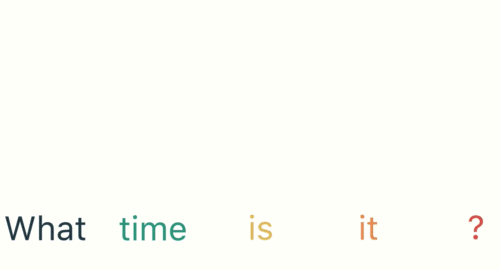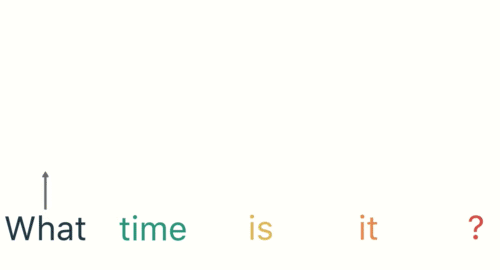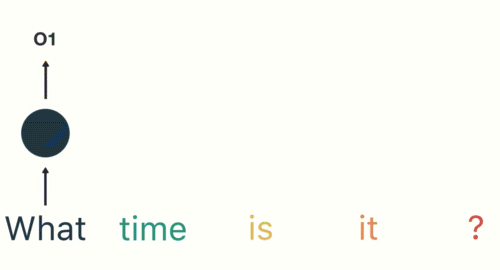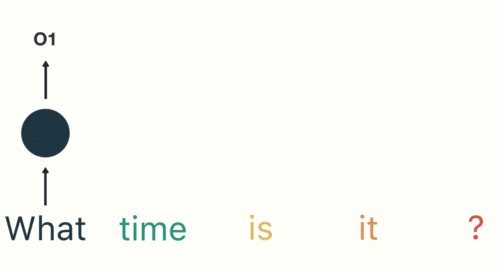
  • 第三步: 继续将单词"time"输送给RNN, 但此时RNN不仅仅利用"time"来产生输出O2, 还会使用来自上一层隐层输出O1作为输入信息.

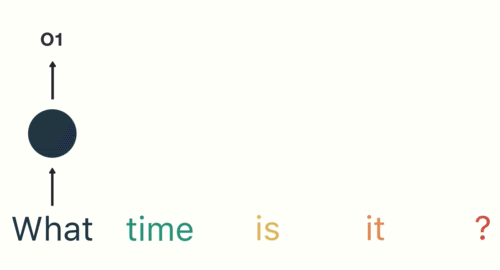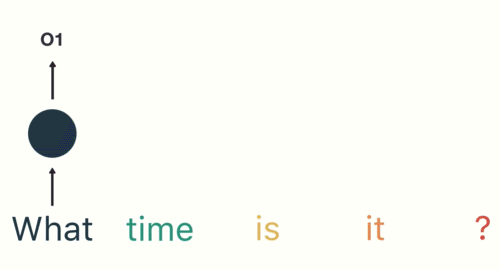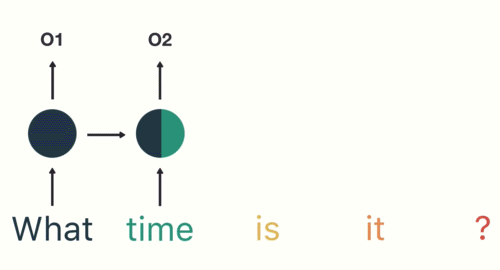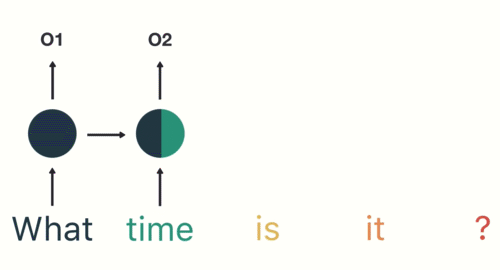
  • 第四步: 重复这样的步骤, 直到处理完所有的单词.


  • 第五步: 最后，将最终的隐层输出O5进行处理来解析用户意图.

  • RNN模型的分类:

    • 这里我们将从两个角度对RNN模型进行分类. 第一个角度是输入和输出的结构, 第二个角度是RNN的内部构造.

  • 按照输入和输出的结构进行分类:

    • N vs N - RNN
    • N vs 1 - RNN
    • 1 vs N - RNN
    • N vs M - RNN

  • 按照RNN的内部构造进行分类:

    • 传统RNN
    • LSTM
    • Bi-LSTM
    • GRU
    • Bi-GRU
  • N vs N - RNN:
    • 它是RNN最基础的结构形式, 最大的特点就是: 输入和输出序列是等长的. 由于这个限制的存在, 使其适用范围比较小, 可用于生成等长度的合辙诗句.

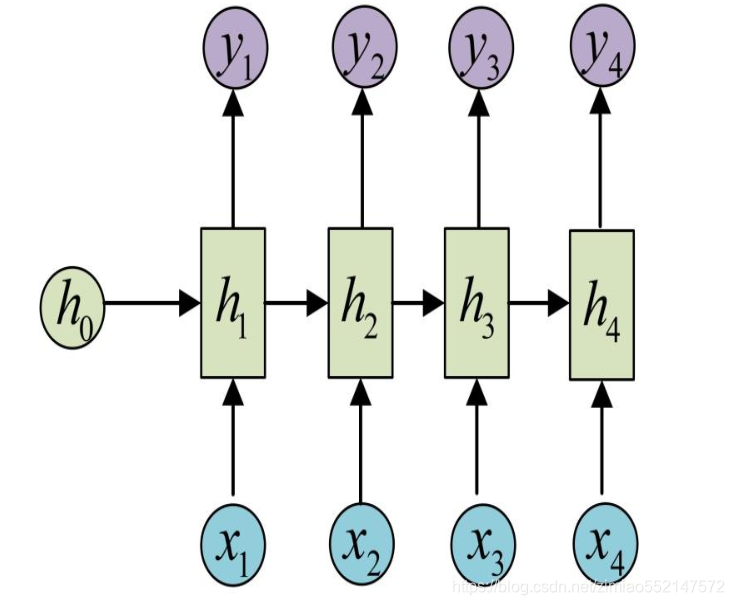
  • N vs 1 - RNN:
    • 有时候我们要处理的问题输入是一个序列，而要求输出是一个单独的值而不是序列，应该怎样建模呢？我们只要在最后一个隐层输出h上进行线性变换就可以了，大部分情况下，为了更好的明确结果, 还要使用sigmoid或者softmax进行处理. 这种结构经常被应用在文本分类问题上.

  • 1 vs N - RNN:
    • 如果输入不是序列而输出为序列的情况怎么处理呢？我们最常采用的一种方式就是使该输入作用于每次的输出之上. 这种结构可用于将图片生成文字任务等.

  • N vs M - RNN:
    • 这是一种不限输入输出长度的RNN结构, 它由编码器和解码器两部分组成, 两者的内部结构都是某类RNN, 它也被称为seq2seq架构. 输入数据首先通过编码器, 最终输出一个隐含变量c, 之后最常用的做法是使用这个隐含变量c作用在解码器进行解码的每一步上, 以保证输入信息被有效利用.

  • seq2seq架构最早被提出应用于机器翻译, 因为其输入输出不受限制，如今也是应用最广的RNN模型结构. 在机器翻译, 阅读理解, 文本摘要等众多领域都进行了非常多的应用实践.
  • 关于RNN的内部构造进行分类的内容我们将在后面使用单独的小节详细讲解.

  • 小节总结:

    • 学习了什么是RNN模型:
      • RNN(Recurrent Neural Network), 中文称作循环神经网络, 它一般以序列数据为输入, 通过网络内部的结构设计有效捕捉序列之间的关系特征, 一般也是以序列形式进行输出.
    • RNN的循环机制使模型隐层上一时间步产生的结果, 能够作为当下时间步输入的一部分(当下时间步的输入除了正常的输入外还包括上一步的隐层输出)对当下时间步的输出产生影响.
    • 学习了RNN模型的作用:
      • 因为RNN结构能够很好利用序列之间的关系, 因此针对自然界具有连续性的输入序列, 如人类的语言, 语音等进行很好的处理, 广泛应用于NLP领域的各项任务, 如文本分类, 情感分析, 意图识别, 机器翻译等.
    • 以一个用户意图识别的例子对RNN的运行过程进行简单的分析:
      • 第一步: 用户输入了"What time is it ?", 我们首先需要对它进行基本的分词, 因为RNN是按照顺序工作的, 每次只接收一个单词进行处理.
      • 第二步: 首先将单词"What"输送给RNN, 它将产生一个输出O1.
      • 第三步: 继续将单词"time"输送给RNN, 但此时RNN不仅仅利用"time"来产生输出O2, 还会使用来自上一层隐层输出O1作为输入信息.
      • 第四步: 重复这样的步骤, 直到处理完所有的单词.
      • 第五步: 最后，将最终的隐层输出O5进行处理来解析用户意图.
    • 学习了RNN模型的分类:
      • 这里我们将从两个角度对RNN模型进行分类. 第一个角度是输入和输出的结构, 第二个角度是RNN的内部构造.
    • 按照输入和输出的结构进行分类:
      • N vs N - RNN
      • N vs 1 - RNN
      • 1 vs N - RNN
      • N vs M - RNN
    • N vs N - RNN:
      • 它是RNN最基础的结构形式, 最大的特点就是: 输入和输出序列是等长的. 由于这个限制的存在, 使其适用范围比较小, 可用于生成等长度的合辙诗句.
    • N vs 1 - RNN:
      • 有时候我们要处理的问题输入是一个序列，而要求输出是一个单独的值而不是序列，应该怎样建模呢？我们只要在最后一个隐层输出h上进行线性变换就可以了，大部分情况下，为了更好的明确结果, 还要使用sigmoid或者softmax进行处理. 这种结构经常被应用在文本分类问题上.
    • 1 vs N - RNN:
      • 如果输入不是序列而输出为序列的情况怎么处理呢？我们最常采用的一种方式就是使该输入作用于每次的输出之上. 这种结构可用于将图片生成文字任务等.
    • N vs M - RNN:
      • 这是一种不限输入输出长度的RNN结构, 它由编码器和解码器两部分组成, 两者的内部结构都是某类RNN, 它也被称为seq2seq架构. 输入数据首先通过编码器, 最终输出一个隐含变量c, 之后最常用的做法是使用这个隐含变量c作用在解码器进行解码的每一步上, 以保证输入信息被有效利用.
      • seq2seq架构最早被提出应用于机器翻译, 因为其输入输出不受限制，如今也是应用最广的RNN模型结构. 在机器翻译, 阅读理解, 文本摘要等众多领域都进行了非常多的应用实践.
    • 按照RNN的内部构造进行分类:
      • 传统RNN
      • LSTM
      • Bi-LSTM
      • GRU
      • Bi-GRU
    • 关于RNN的内部构造进行分类的内容我们将在后面使用单独的小节详细讲解.

1.2 传统RNN模型

  • 学习目标:
    • 了解传统RNN的内部结构及计算公式.
    • 掌握Pytorch中传统RNN工具的使用.
    • 了解传统RNN的优势与缺点.
  • 传统RNN的内部结构图:

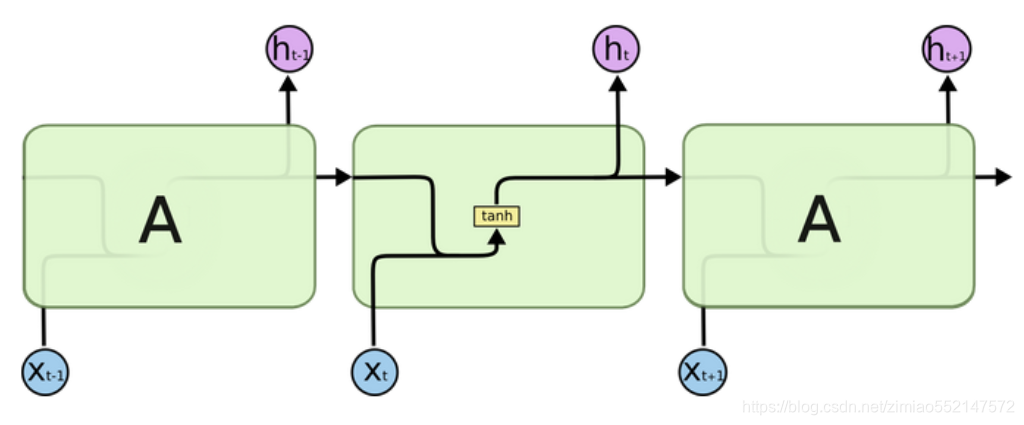
  • 结构解释图:

  • 内部结构分析:
    • 我们把目光集中在中间的方块部分, 它的输入有两部分, 分别是h(t-1)以及x(t), 代表上一时间步的隐层输出, 以及此时间步的输入, 它们进入RNN结构体后, 会"融合"到一起, 这种融合我们根据结构解释可知, 是将二者进行拼接, 形成新的张量[x(t), h(t-1)], 之后这个新的张量将通过一个全连接层(线性层), 该层使用tanh作为激活函数, 最终得到该时间步的输出h(t), 它将作为下一个时间步的输入和x(t+1)一起进入结构体. 以此类推.
  • 内部结构过程演示:

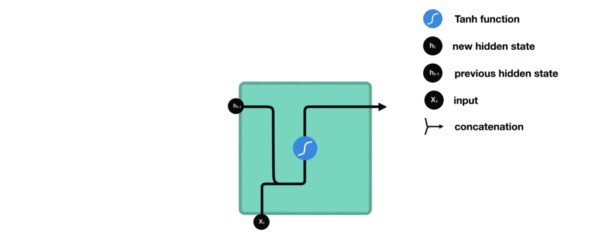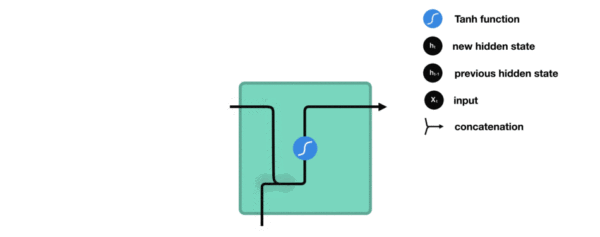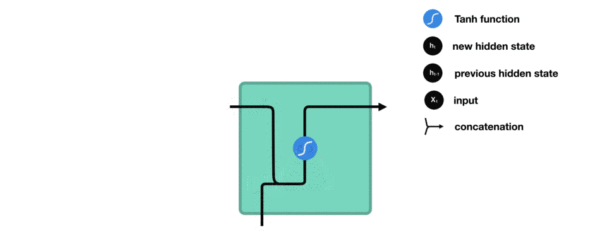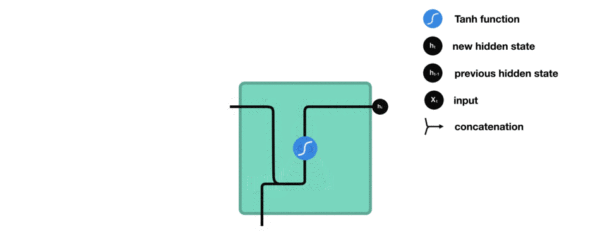
  • 根据结构分析得出内部计算公式:

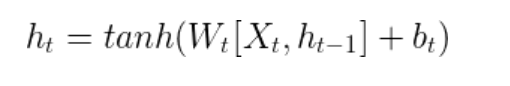
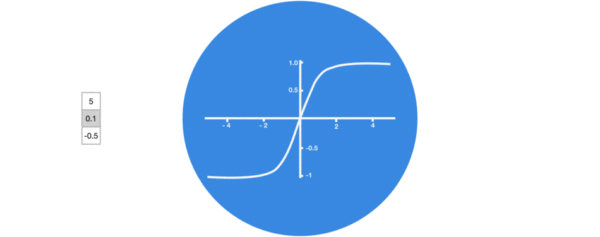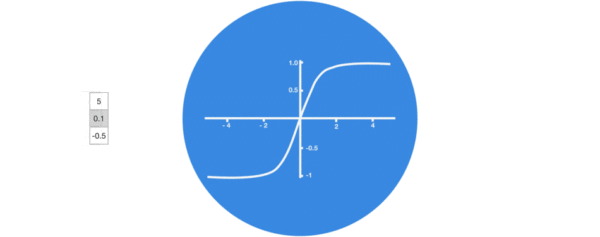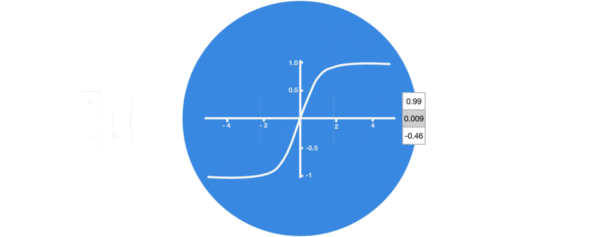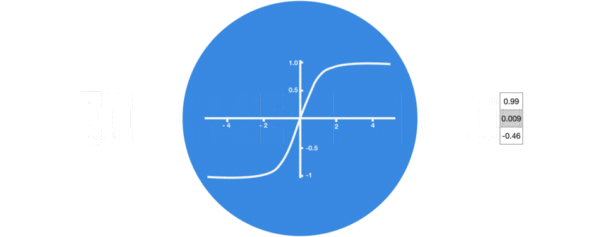
  • 激活函数tanh的作用:
    • 用于帮助调节流经网络的值, tanh函数将值压缩在-1和1之间.

  • Pytorch中传统RNN工具的使用:

    • 位置: 在torch.nn工具包之中, 通过torch.nn.RNN可调用.
  • nn.RNN类初始化主要参数解释:
    • input_size: 输入张量x中特征维度的大小.
    • hidden_size: 隐层张量h中特征维度的大小.
    • num_layers: 隐含层的数量.
    • nonlinearity: 激活函数的选择, 默认是tanh.
  • nn.RNN类实例化对象主要参数解释:
    • input: 输入张量x.
    • h0: 初始化的隐层张量h.
  • nn.RNN使用示例:
  1. >>> import torch
  2. >>> import torch.nn as nn
  3. >>> rnn = nn.RNN(5, 6, 1)
  4. >>> input = torch.randn(1, 3, 5)
  5. >>> h0 = torch.randn(1, 3, 6)
  6. >>> output, hn = rnn(input, h0)
  7. >>> output
  8. tensor([[[ 0.4282, -0.8475, -0.0685, -0.4601, -0.8357,  0.1252],
  9.          [ 0.5758, -0.2823,  0.4822, -0.4485, -0.7362,  0.0084],
  10.          [ 0.9224, -0.7479, -0.3682, -0.5662, -0.9637,  0.4938]]],
  11.        grad_fn=<StackBackward>)
  12.  
  13. >>> hn
  14. tensor([[[ 0.4282, -0.8475, -0.0685, -0.4601, -0.8357,  0.1252],
  15.          [ 0.5758, -0.2823,  0.4822, -0.4485, -0.7362,  0.0084],
  16.          [ 0.9224, -0.7479, -0.3682, -0.5662, -0.9637,  0.4938]]],
  17.        grad_fn=<StackBackward>)
  • 传统RNN的优势:
    • 由于内部结构简单, 对计算资源要求低, 相比之后我们要学习的RNN变体:LSTM和GRU模型参数总量少了很多, 在短序列任务上性能和效果都表现优异.
  • 传统RNN的缺点:
    • 传统RNN在解决长序列之间的关联时, 通过实践，证明经典RNN表现很差, 原因是在进行反向传播的时候, 过长的序列导致梯度的计算异常, 发生梯度消失或爆炸.
  • 什么是梯度消失或爆炸呢？
    • 根据反向传播算法和链式法则, 梯度的计算可以简化为以下公式:

  • 其中sigmoid的导数值域是固定的, 在[0, 0.25]之间, 而一旦公式中的w也小于1, 那么通过这样的公式连乘后, 最终的梯度就会变得非常非常小, 这种现象称作梯度消失. 反之, 如果我们人为的增大w的值, 使其大于1, 那么连乘够就可能造成梯度过大, 称作梯度爆炸.

  • 梯度消失或爆炸的危害:

    • 如果在训练过程中发生了梯度消失，权重无法被更新，最终导致训练失败; 梯度爆炸所带来的梯度过大，大幅度更新网络参数，在极端情况下，结果会溢出（NaN值）.

  • 小节总结:

    • 学习了传统RNN的结构并进行了分析;
      • 它的输入有两部分, 分别是h(t-1)以及x(t), 代表上一时间步的隐层输出, 以及此时间步的输入, 它们进入RNN结构体后, 会"融合"到一起, 这种融合我们根据结构解释可知, 是将二者进行拼接, 形成新的张量[x(t), h(t-1)], 之后这个新的张量将通过一个全连接层(线性层), 该层使用tanh作为激活函数, 最终得到该时间步的输出h(t), 它将作为下一个时间步的输入和x(t+1)一起进入结构体. 以此类推.
    • 根据结构分析得出了传统RNN的计算公式.
    • 学习了激活函数tanh的作用:
      • 用于帮助调节流经网络的值, tanh函数将值压缩在-1和1之间.
    • 学习了Pytorch中传统RNN工具的使用:
      • 位置: 在torch.nn工具包之中, 通过torch.nn.RNN可调用.
    • nn.RNN类初始化主要参数解释:
      • input_size: 输入张量x中特征维度的大小.
      • hidden_size: 隐层张量h中特征维度的大小.
      • num_layers: 隐含层的数量.
      • nonlinearity: 激活函数的选择, 默认是tanh.
    • nn.RNN类实例化对象主要参数解释:
      • input: 输入张量x.
      • h0: 初始化的隐层张量h.
    • 实现了nn.RNN的使用示例, 获得RNN的真实返回结果样式.
    • 学习了传统RNN的优势:
      • 由于内部结构简单, 对计算资源要求低, 相比之后我们要学习的RNN变体:LSTM和GRU模型参数总量少了很多, 在短序列任务上性能和效果都表现优异.
    • 学习了传统RNN的缺点:
      • 传统RNN在解决长序列之间的关联时, 通过实践，证明经典RNN表现很差, 原因是在进行反向传播的时候, 过长的序列导致梯度的计算异常, 发生梯度消失或爆炸.
    • 学习了什么是梯度消失或爆炸:
      • 根据反向传播算法和链式法则, 得到梯度的计算的简化公式:其中sigmoid的导数值域是固定的, 在[0, 0.25]之间, 而一旦公式中的w也小于1, 那么通过这样的公式连乘后, 最终的梯度就会变得非常非常小, 这种现象称作梯度消失. 反之, 如果我们人为的增大w的值, 使其大于1, 那么连乘够就可能造成梯度过大, 称作梯度爆炸.
    • 梯度消失或爆炸的危害:
      • 如果在训练过程中发生了梯度消失，权重无法被更新，最终导致训练失败; 梯度爆炸所带来的梯度过大，大幅度更新网络参数，在极端情况下，结果会溢出（NaN值）.

1.3 LSTM模型

  • 学习目标:
    • 了解LSTM内部结构及计算公式.
    • 掌握Pytorch中LSTM工具的使用.
    • 了解LSTM的优势与缺点.
  • LSTM（Long Short-Term Memory）也称长短时记忆结构, 它是传统RNN的变体, 与经典RNN相比能够有效捕捉长序列之间的语义关联, 缓解梯度消失或爆炸现象. 同时LSTM的结构更复杂, 它的核心结构可以分为四个部分去解析:
    • 遗忘门
    • 输入门
    • 细胞状态
    • 输出门
  • LSTM的内部结构图:

  • 结构解释图:

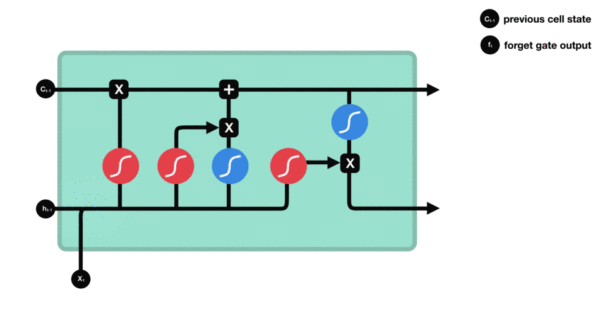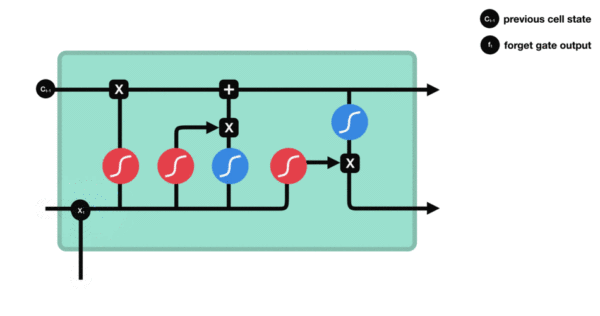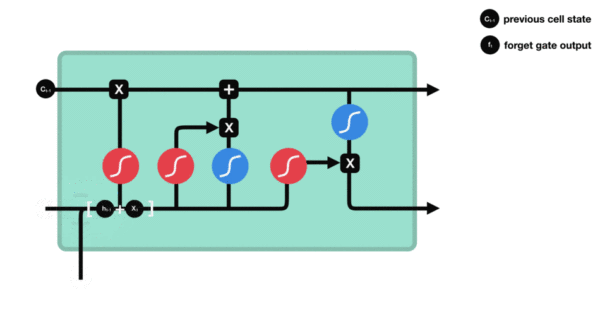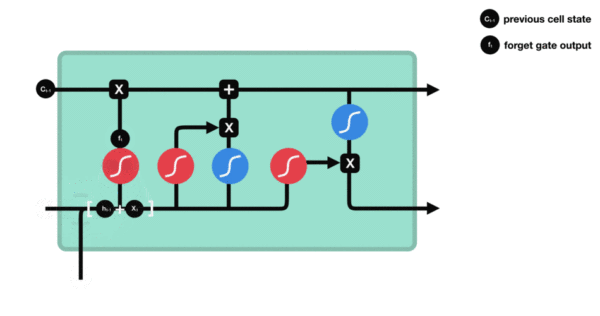
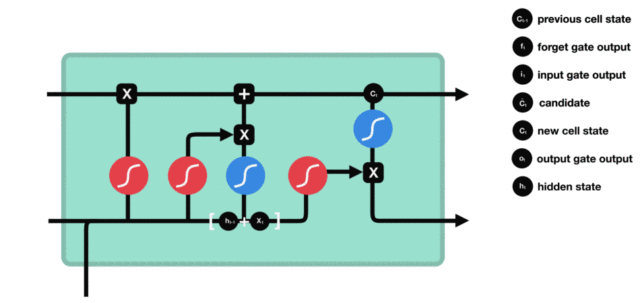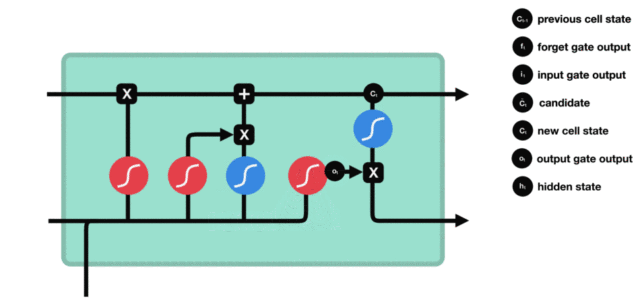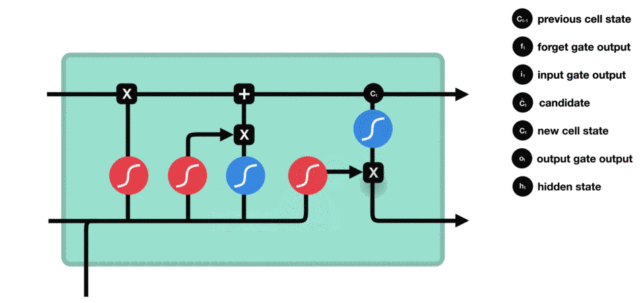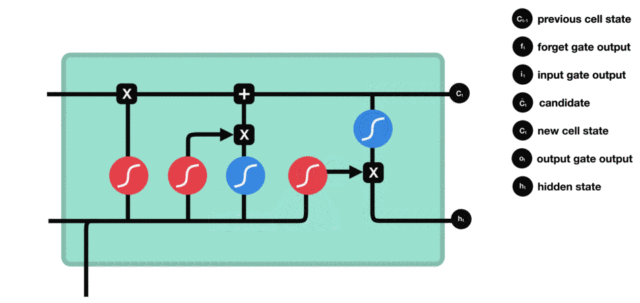
  • 遗忘门部分结构图与计算公式:

  • 遗忘门结构分析:
    • 与传统RNN的内部结构计算非常相似, 首先将当前时间步输入x(t)与上一个时间步隐含状态h(t-1)拼接, 得到[x(t), h(t-1)], 然后通过一个全连接层做变换, 最后通过sigmoid函数进行激活得到f(t), 我们可以将f(t)看作是门值, 好比一扇门开合的大小程度, 门值都将作用在通过该扇门的张量, 遗忘门门值将作用的上一层的细胞状态上, 代表遗忘过去的多少信息, 又因为遗忘门门值是由x(t), h(t-1)计算得来的, 因此整个公式意味着根据当前时间步输入和上一个时间步隐含状态h(t-1)来决定遗忘多少上一层的细胞状态所携带的过往信息.
  • 遗忘门内部结构过程演示:

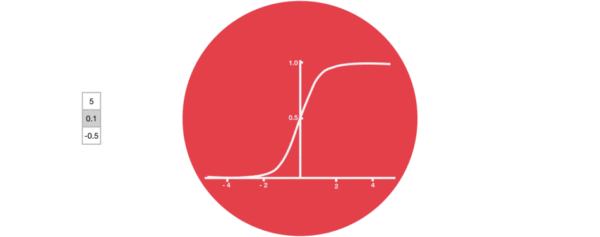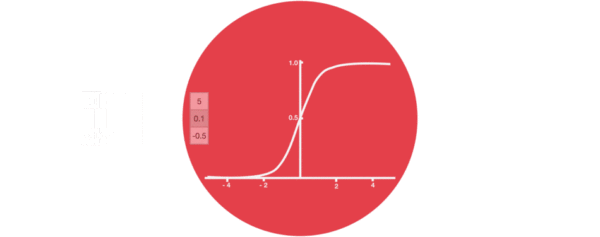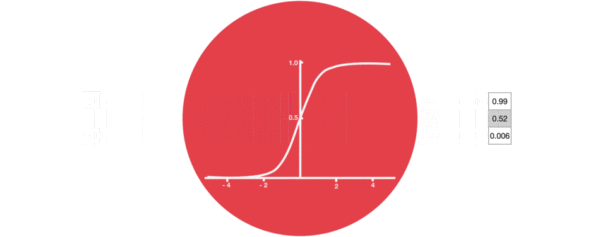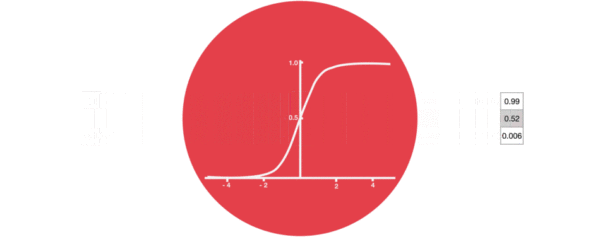
  • 激活函数sigmiod的作用:
    • 用于帮助调节流经网络的值, sigmoid函数将值压缩在0和1之间.

  • 输入门部分结构图与计算公式:

  • 输入门结构分析:
    • 我们看到输入门的计算公式有两个, 第一个就是产生输入门门值的公式, 它和遗忘门公式几乎相同, 区别只是在于它们之后要作用的目标上. 这个公式意味着输入信息有多少需要进行过滤. 输入门的第二个公式是与传统RNN的内部结构计算相同. 对于LSTM来讲, 它得到的是当前的细胞状态, 而不是像经典RNN一样得到的是隐含状态.
  • 输入门内部结构过程演示:

  • 细胞状态更新图与计算公式:

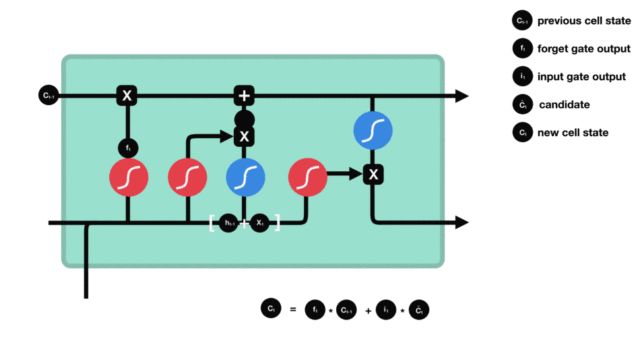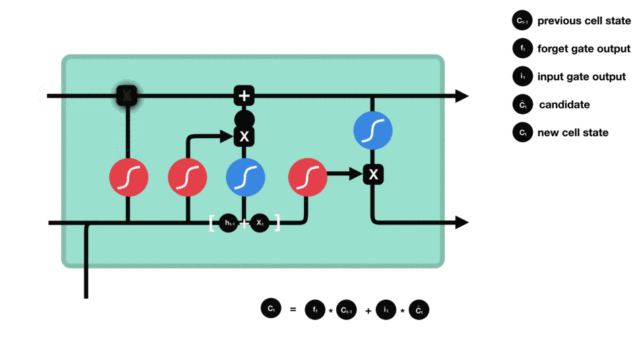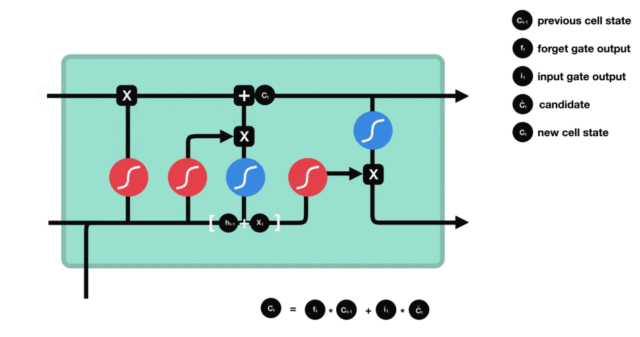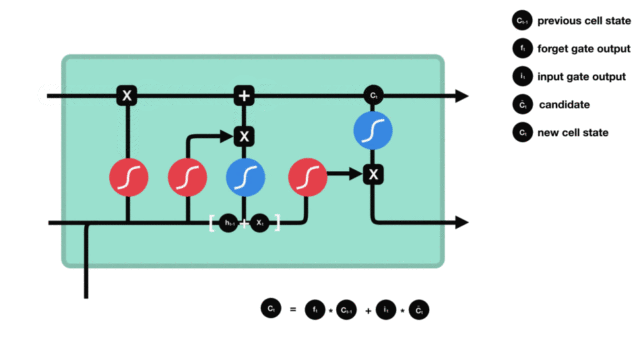
  • 细胞状态更新分析:
    • 细胞更新的结构与计算公式非常容易理解, 这里没有全连接层, 只是将刚刚得到的遗忘门门值与上一个时间步得到的C(t-1)相乘, 再加上输入门门值与当前时间步得到的未更新C(t)相乘的结果. 最终得到更新后的C(t)作为下一个时间步输入的一部分. 整个细胞状态更新过程就是对遗忘门和输入门的应用.
  • 细胞状态更新过程演示:

  • 输出门部分结构图与计算公式:

  • 输出门结构分析:
    • 输出门部分的公式也是两个, 第一个即是计算输出门的门值, 它和遗忘门，输入门计算方式相同. 第二个即是使用这个门值产生隐含状态h(t), 他将作用在更新后的细胞状态C(t)上, 并做tanh激活, 最终得到h(t)作为下一时间步输入的一部分. 整个输出门的过程, 就是为了产生隐含状态h(t).
  • 输出门内部结构过程演示:

  • 什么是Bi-LSTM ?
    • Bi-LSTM即双向LSTM, 它没有改变LSTM本身任何的内部结构, 只是将LSTM应用两次且方向不同, 再将两次得到的LSTM结果进行拼接作为最终输出.

  • Bi-LSTM结构分析:
    • 我们看到图中对"我爱中国"这句话或者叫这个输入序列, 进行了从左到右和从右到左两次LSTM处理, 将得到的结果张量进行了拼接作为最终输出. 这种结构能够捕捉语言语法中一些特定的前置或后置特征, 增强语义关联,但是模型参数和计算复杂度也随之增加了一倍, 一般需要对语料和计算资源进行评估后决定是否使用该结构.
  • Pytorch中LSTM工具的使用:
    • 位置: 在torch.nn工具包之中, 通过torch.nn.LSTM可调用.
  • nn.LSTM类初始化主要参数解释:
    • input_size: 输入张量x中特征维度的大小.
    • hidden_size: 隐层张量h中特征维度的大小.
    • num_layers: 隐含层的数量.
    • nonlinearity: 激活函数的选择, 默认是tanh.
    • bidirectional: 是否选择使用双向LSTM, 如果为True, 则使用; 默认不使用.
  • nn.LSTM类实例化对象主要参数解释:
    • input: 输入张量x.
    • h0: 初始化的隐层张量h.
    • c0: 初始化的细胞状态张量c.
  • nn.LSTM使用示例:
  1. >>> import torch.nn as nn
  2. >>> import torch
  3. >>> rnn = nn.LSTM(5, 6, 2)
  4. >>> input = torch.randn(1, 3, 5)
  5. >>> h0 = torch.randn(2, 3, 6)
  6. >>> c0 = torch.randn(2, 3, 6)
  7. >>> output, (hn, cn) = rnn(input, (h0, c0))
  8. >>> output
  9. tensor([[[ 0.0447, -0.0335,  0.1454,  0.0438,  0.0865,  0.0416],
  10.          [ 0.0105,  0.1923,  0.5507, -0.1742,  0.1569, -0.0548],
  11.          [-0.1186,  0.1835, -0.0022, -0.1388, -0.0877, -0.4007]]],
  12.        grad_fn=<StackBackward>)
  13. >>> hn
  14. tensor([[[ 0.4647, -0.2364,  0.0645, -0.3996, -0.0500, -0.0152],
  15.          [ 0.3852,  0.0704,  0.2103, -0.2524,  0.0243,  0.0477],
  16.          [ 0.2571,  0.0608,  0.2322,  0.1815, -0.0513, -0.0291]],
  17.  
  18.         [[ 0.0447, -0.0335,  0.1454,  0.0438,  0.0865,  0.0416],
  19.          [ 0.0105,  0.1923,  0.5507, -0.1742,  0.1569, -0.0548],
  20.          [-0.1186,  0.1835, -0.0022, -0.1388, -0.0877, -0.4007]]],
  21.        grad_fn=<StackBackward>)
  22. >>> cn
  23. tensor([[[ 0.8083, -0.5500,  0.1009, -0.5806, -0.0668, -0.1161],
  24.          [ 0.7438,  0.0957,  0.5509, -0.7725,  0.0824,  0.0626],
  25.          [ 0.3131,  0.0920,  0.8359,  0.9187, -0.4826, -0.0717]],
  26.  
  27.         [[ 0.1240, -0.0526,  0.3035,  0.1099,  0.5915,  0.0828],
  28.          [ 0.0203,  0.8367,  0.9832, -0.4454,  0.3917, -0.1983],
  29.          [-0.2976,  0.7764, -0.0074, -0.1965, -0.1343, -0.6683]]],
  30.        grad_fn=<StackBackward>)
  • LSTM优势:
    • LSTM的门结构能够有效减缓长序列问题中可能出现的梯度消失或爆炸, 虽然并不能杜绝这种现象, 但在更长的序列问题上表现优于传统RNN.
  • LSTM缺点:
    • 由于内部结构相对较复杂, 因此训练效率在同等算力下较传统RNN低很多.

  • 小节总结:

    • LSTM（Long Short-Term Memory）也称长短时记忆结构, 它是传统RNN的变体, 与经典RNN相比能够有效捕捉长序列之间的语义关联, 缓解梯度消失或爆炸现象. 同时LSTM的结构更复杂, 它的核心结构可以分为四个部分去解析:
      • 遗忘门
      • 输入门
      • 细胞状态
      • 输出门
    • 遗忘门结构分析:
      • 与传统RNN的内部结构计算非常相似, 首先将当前时间步输入x(t)与上一个时间步隐含状态h(t-1)拼接, 得到[x(t), h(t-1)], 然后通过一个全连接层做变换, 最后通过sigmoid函数进行激活得到f(t), 我们可以将f(t)看作是门值, 好比一扇门开合的大小程度, 门值都将作用在通过该扇门的张量, 遗忘门门值将作用的上一层的细胞状态上, 代表遗忘过去的多少信息, 又因为遗忘门门值是由x(t), h(t-1)计算得来的, 因此整个公式意味着根据当前时间步输入和上一个时间步隐含状态h(t-1)来决定遗忘多少上一层的细胞状态所携带的过往信息.
    • 输入门结构分析:
      • 我们看到输入门的计算公式有两个, 第一个就是产生输入门门值的公式, 它和遗忘门公式几乎相同, 区别只是在于它们之后要作用的目标上. 这个公式意味着输入信息有多少需要进行过滤. 输入门的第二个公式是与传统RNN的内部结构计算相同. 对于LSTM来讲, 它得到的是当前的细胞状态, 而不是像经典RNN一样得到的是隐含状态.
    • 细胞状态更新分析:
      • 细胞更新的结构与计算公式非常容易理解, 这里没有全连接层, 只是将刚刚得到的遗忘门门值与上一个时间步得到的C(t-1)相乘, 再加上输入门门值与当前时间步得到的未更新C(t)相乘的结果. 最终得到更新后的C(t)作为下一个时间步输入的一部分. 整个细胞状态更新过程就是对遗忘门和输入门的应用.
    • 输出门结构分析:
      • 输出门部分的公式也是两个, 第一个即是计算输出门的门值, 它和遗忘门，输入门计算方式相同. 第二个即是使用这个门值产生隐含状态h(t), 他将作用在更新后的细胞状态C(t)上, 并做tanh激活, 最终得到h(t)作为下一时间步输入的一部分. 整个输出门的过程, 就是为了产生隐含状态h(t).
    • 什么是Bi-LSTM ?
      • Bi-LSTM即双向LSTM, 它没有改变LSTM本身任何的内部结构, 只是将LSTM应用两次且方向不同, 再将两次得到的LSTM结果进行拼接作为最终输出.
    • Pytorch中LSTM工具的使用:
      • 位置: 在torch.nn工具包之中, 通过torch.nn.LSTM可调用.
    • LSTM优势:
      • LSTM的门结构能够有效减缓长序列问题中可能出现的梯度消失或爆炸, 虽然并不能杜绝这种现象, 但在更长的序列问题上表现优于传统RNN.
    • LSTM缺点:
      • 由于内部结构相对较复杂, 因此训练效率在同等算力下较传统RNN低很多.

1.4 GRU模型

  • 学习目标:
    • 了解GRU内部结构及计算公式.
    • 掌握Pytorch中GRU工具的使用.
    • 了解GRU的优势与缺点.
  • GRU（Gated Recurrent Unit）也称门控循环单元结构, 它也是传统RNN的变体, 同LSTM一样能够有效捕捉长序列之间的语义关联, 缓解梯度消失或爆炸现象. 同时它的结构和计算要比LSTM更简单, 它的核心结构可以分为两个部分去解析:
    • 更新门
    • 重置门
  • GRU的内部结构图和计算公式:

  • 结构解释图:

  • GRU的更新门和重置门结构图:

  • 内部结构分析:
    • 和之前分析过的LSTM中的门控一样, 首先计算更新门和重置门的门值, 分别是z(t)和r(t), 计算方法就是使用X(t)与h(t-1)拼接进行线性变换, 再经过sigmoid激活. 之后重置门门值作用在了h(t-1)上, 代表控制上一时间步传来的信息有多少可以被利用. 接着就是使用这个重置后的h(t-1)进行基本的RNN计算, 即与x(t)拼接进行线性变化, 经过tanh激活, 得到新的h(t). 最后更新门的门值会作用在新的h(t)，而1-门值会作用在h(t-1)上, 随后将两者的结果相加, 得到最终的隐含状态输出h(t), 这个过程意味着更新门有能力保留之前的结果, 当门值趋于1时, 输出就是新的h(t), 而当门值趋于0时, 输出就是上一时间步的h(t-1).
  • Bi-GRU与Bi-LSTM的逻辑相同, 都是不改变其内部结构, 而是将模型应用两次且方向不同, 再将两次得到的LSTM结果进行拼接作为最终输出. 具体参见上小节中的Bi-LSTM.
  • Pytorch中GRU工具的使用:
    • 位置: 在torch.nn工具包之中, 通过torch.nn.GRU可调用.
  • nn.GRU类初始化主要参数解释:
    • input_size: 输入张量x中特征维度的大小.
    • hidden_size: 隐层张量h中特征维度的大小.
    • num_layers: 隐含层的数量.
    • nonlinearity: 激活函数的选择, 默认是tanh.
    • bidirectional: 是否选择使用双向LSTM, 如果为True, 则使用; 默认不使用.
  • nn.GRU类实例化对象主要参数解释:
    • input: 输入张量x.
    • h0: 初始化的隐层张量h.
  • nn.GRU使用示例:
  1. >>> import torch
  2. >>> import torch.nn as nn
  3. >>> rnn = nn.GRU(5, 6, 2)
  4. >>> input = torch.randn(1, 3, 5)
  5. >>> h0 = torch.randn(2, 3, 6)
  6. >>> output, hn = rnn(input, h0)
  7. >>> output
  8. tensor([[[-0.2097, -2.2225,  0.6204, -0.1745, -0.1749, -0.0460],
  9.          [-0.3820,  0.0465, -0.4798,  0.6837, -0.7894,  0.5173],
  10.          [-0.0184, -0.2758,  1.2482,  0.5514, -0.9165, -0.6667]]],
  11.        grad_fn=<StackBackward>)
  12. >>> hn
  13. tensor([[[ 0.6578, -0.4226, -0.2129, -0.3785,  0.5070,  0.4338],
  14.          [-0.5072,  0.5948,  0.8083,  0.4618,  0.1629, -0.1591],
  15.          [ 0.2430, -0.4981,  0.3846, -0.4252,  0.7191,  0.5420]],
  16.  
  17.         [[-0.2097, -2.2225,  0.6204, -0.1745, -0.1749, -0.0460],
  18.          [-0.3820,  0.0465, -0.4798,  0.6837, -0.7894,  0.5173],
  19.          [-0.0184, -0.2758,  1.2482,  0.5514, -0.9165, -0.6667]]],
  20.        grad_fn=<StackBackward>)
  • GRU的优势:
    • GRU和LSTM作用相同, 在捕捉长序列语义关联时, 能有效抑制梯度消失或爆炸, 效果都优于传统RNN且计算复杂度相比LSTM要小.
  • GRU的缺点:
    • GRU仍然不能完全解决梯度消失问题, 同时其作用RNN的变体, 有着RNN结构本身的一大弊端, 即不可并行计算, 这在数据量和模型体量逐步增大的未来, 是RNN发展的关键瓶颈.

  • 小节总结:

    • GRU（Gated Recurrent Unit）也称门控循环单元结构, 它也是传统RNN的变体, 同LSTM一样能够有效捕捉长序列之间的语义关联, 缓解梯度消失或爆炸现象. 同时它的结构和计算要比LSTM更简单, 它的核心结构可以分为两个部分去解析:
      • 更新门
      • 重置门
    • 内部结构分析:
      • 和之前分析过的LSTM中的门控一样, 首先计算更新门和重置门的门值, 分别是z(t)和r(t), 计算方法就是使用X(t)与h(t-1)拼接进行线性变换, 再经过sigmoid激活. 之后重置门门值作用在了h(t-1)上, 代表控制上一时间步传来的信息有多少可以被利用. 接着就是使用这个重置后的h(t-1)进行基本的RNN计算, 即与x(t)拼接进行线性变化, 经过tanh激活, 得到新的h(t). 最后更新门的门值会作用在新的h(t)，而1-门值会作用在h(t-1)上, 随后将两者的结果相加, 得到最终的隐含状态输出h(t), 这个过程意味着更新门有能力保留之前的结果, 当门值趋于1时, 输出就是新的h(t), 而当门值趋于0时, 输出就是上一时间步的h(t-1).
    • Bi-GRU与Bi-LSTM的逻辑相同, 都是不改变其内部结构, 而是将模型应用两次且方向不同, 再将两次得到的LSTM结果进行拼接作为最终输出. 具体参见上小节中的Bi-LSTM.
    • Pytorch中GRU工具的使用:
      • 位置: 在torch.nn工具包之中, 通过torch.nn.GRU可调用.
    • GRU的优势:
      • GRU和LSTM作用相同, 在捕捉长序列语义关联时, 能有效抑制梯度消失或爆炸, 效果都优于传统RNN且计算复杂度相比LSTM要小.
    • GRU的缺点:
      • GRU仍然不能完全解决梯度消失问题, 同时其作用RNN的变体, 有着RNN结构本身的一大弊端, 即不可并行计算, 这在数据量和模型体量逐步增大的未来, 是RNN发展的关键瓶颈.

  1. weight_ih_l[k]
  2.     第k层的可学习输入隐藏权重的形状 (hidden_size, input_size) 
  3.     对于“k=0”。否则，形状是 (hidden_size, num_directions * hidden_size) 
  4.  
  5. weight_ih: 
  6.     可学习输入隐藏权重的形状(hidden_size, input_size)
  7.     每个单词 的嵌入维度的 向量 作为 一个时间步 输入到 一个 RNN 节点，
  8.     然后 会和 神经元数量维度的 向量 构成一个 可学习输入隐藏权重 这样的 形状 (hidden_size, input_size)，
  9.     就是 (神经元数量, 单词嵌入维度)。
  10.  
  11. def __init__(self, mode, input_size, hidden_size, 
  12.                     num_layers=1, bias=True, batch_first=False, dropout=0., 
  13.                     bidirectional=False):
  14.     #默认值bidirectional=False：那么“2 if False else 1”返回1，“2 if True else 1”返回2。
  15.     #如果RNN是双向的，num_directions应该是2，否则应该是1。
  16.     num_directions = 2 if bidirectional else 1                    
  17.         
  18. ========================================================================
  19. # nn.RNN(输入数据的词嵌入维度, 隐藏层中神经元数量, 隐藏层层数)
  20. rnn = nn.RNN(5, 6, 2)
  21. rnn = nn.GRU(5, 6, 2)
  22. rnn = nn.LSTM(5, 6, 2)
  23.  
  24. # input of shape (seq_len, batch, input_size)：(当前批次的样本个数, 当前样本的序列长度(单词个数), 词嵌入维度)
  25. # input输入数据，torch.randn(当前批次的样本个数, 当前样本的序列长度(单词个数), 词嵌入维度)
  26. input = torch.randn(4, 3, 5)
  27.  
  28. # h_0 of shape (num_layers * num_directions, batch, hidden_size)：
  29. #	RNN是单向：(隐藏层层数 * 1, 一个句子单词个数, 隐藏层中神经元数量)	
  30. #	RNN是双向：(隐藏层层数 * 2, 一个句子单词个数, 隐藏层中神经元数量)	
  31. # hn隐藏层数据，torch.randn(隐藏层层数, 当前样本的序列长度(单词个数), 隐藏层中神经元数量)
  32. h0 = torch.randn(2, 3, 6)
  33.  
  34. # c_0 of shape (num_layers * num_directions, batch, hidden_size) 
  35. #	RNN是单向：(隐藏层层数 * 1, 一个句子单词个数, 隐藏层中神经元数量)	
  36. #	RNN是双向：(隐藏层层数 * 2, 一个句子单词个数, 隐藏层中神经元数量)	
  37. c0 = torch.randn(2, 3, 6)
  38.  
  39. output, hn = rnn(input, h0)
  40. output, (hn, cn) = rnn(input, (h0, c0))
  41.  
  42. # output of shape (seq_len, batch, num_directions * hidden_size):
  43. #	RNN是单向：(当前批次的样本个数, 当前样本的序列长度(单词个数), 隐藏层中神经元数量 * 1)	
  44. #	RNN是双向：(当前批次的样本个数, 当前样本的序列长度(单词个数), 隐藏层中神经元数量 * 2)		
  45. output.shape #torch.Size([4, 3, 6])
  46.  
  47. # h_n of shape (num_layers * num_directions, batch, hidden_size)
  48. #	RNN是单向：(隐藏层层数 * 1, 一个句子单词个数, 隐藏层中神经元数量)	
  49. #	RNN是双向：(隐藏层层数 * 2, 一个句子单词个数, 隐藏层中神经元数量)	
  50. hn.shape #torch.Size([2, 3, 6])
  51.  
  52. # c_n of shape (num_layers * num_directions, batch, hidden_size)
  53. #	RNN是单向：(隐藏层层数 * 1, 一个句子单词个数, 隐藏层中神经元数量)	
  54. #	RNN是双向：(隐藏层层数 * 2, 一个句子单词个数, 隐藏层中神经元数量)
  55. hn.shape #torch.Size([2, 3, 6])
  56. ========================================================================
  57.  
  58. Examples::
  59.     #nn.LSTM(输入数据的词嵌入维度 10, 隐藏层中神经元数量 20, 隐藏层层数 2)
  60.     >>> rnn = nn.LSTM(10, 20, 2)
  61.     #input输入数据，torch.randn(当前批次的样本个数 5, 当前样本的序列长度(单词个数) 3, 词嵌入维度 10)
  62.     >>> input = torch.randn(5, 3, 10)
  63.     #h0/hn隐藏层数据，torch.randn(隐藏层层数 2, 当前样本的序列长度(单词个数) 3, 隐藏层中神经元数量 20)
  64.     >>> h0 = torch.randn(2, 3, 20)
  65.     #c0/cn细胞状态数据，torch.randn(隐藏层层数 2, 当前样本的序列长度(单词个数) 3, 隐藏层中神经元数量 20)
  66.     >>> c0 = torch.randn(2, 3, 20)
  67.     >>> output, (hn, cn) = rnn(input, (h0, c0))

RNN

  1. weight_ih: 
  2.     可学习输入隐藏权重的形状(hidden_size, input_size)
  3.     每个单词 的嵌入维度的 向量 作为 一个时间步 输入到 一个 RNN 节点，
  4.     然后 会和 神经元数量维度的 向量 构成一个 可学习输入隐藏权重 这样的 形状 (hidden_size, input_size)，
  5.     就是 (神经元数量, 单词嵌入维度)。

  1. nn.RNN(输入数据的词嵌入维度, 隐藏层中神经元数量, 隐藏层层数)
  2. Xt：输入数据，shape为(当前批次的样本个数, 当前样本的序列长度(单词个数), 词嵌入维度影)，比如[1,3,5]。
  3. h0：隐藏层数据，shape为(隐藏层层数, 当前样本的序列长度(单词个数), 隐藏层中神经元数量)，比如[1,3,6]。
  4. [Xt,ht-1]：通过concat(Xt,ht-1)把[1,3,5]和[1,3,6]进行列维度(最后一个维度)的拼接变成[1,3,11]。
  5. Wt[Xt,ht-1]：concat拼接后的[1,3,11]乘以Wt的[11,6]变成[1,3,6]。
  6. output是hn隐藏层中的最后一层输出，比如：
  7. 	当隐藏层只有一层时，rnn的输出output和隐藏层数据hn 两者完全相同，shape均为[1,3,6]。
  8. 	当隐藏层有多层时，rnn的输出output为隐藏层数据hn中的最后一个二维矩阵，比如hn为[2,3,6]，output的数据实际为hn中最后一个二维矩阵[1,3,6]。

LSTM

  1. 1.激活函数sigmiod的作用：用于帮助调节流经网络的值, sigmoid函数将值压缩在0和1之间的小数值(相当于一个百分比值)。
  2.   只要是sigmiod输出的百分比值(比如ft/it/ot) 都可作为控制阈值(保留信息比例值)，用于控制流经的数据保留多少。
  3. 2.比如此处的遗忘门中的通过sigmiod输出的ft便是一个0和1之间的小数值，ft用作在“细胞状态更新公式”中的ft*Ct-1，
  4.   因为ft本身就是一个0和1之间的小数值(相当于一个百分比值)，那么ft*Ct-1表示使用ft这个百分值保留多少Ct-1的值。

  1. 1.激活函数sigmiod的作用：用于帮助调节流经网络的值, sigmoid函数将值压缩在0和1之间的小数值(相当于一个百分比值)。
  2.   只要是sigmiod输出的百分比值(比如ft/it/ot) 都可作为控制阈值(保留信息比例值)，用于控制流经的数据保留多少。
  3. 2.比如此处输入门中的通过sigmiod输出的it便是一个0和1之间的小数值，it用作在“细胞状态更新公式”中的it*Ct~，
  4.   因为it本身就是一个0和1之间的小数值(相当于一个百分比值)，那么it*Ct~表示使用it这个百分值保留多少Ct~的值。

  1. 1.激活函数sigmiod的作用：用于帮助调节流经网络的值, sigmoid函数将值压缩在0和1之间的小数值(相当于一个百分比值)。
  2.   只要是sigmiod输出的百分比值(比如ft/it/ot) 都可作为控制阈值(保留信息比例值)，用于控制流经的数据保留多少。
  3. 2.比如输入门中的通过sigmiod输出的it便是一个0和1之间的小数值，it用作在“细胞状态更新公式”中的it*Ct~，
  4.   因为it本身就是一个0和1之间的小数值(相当于一个百分比值)，那么it*Ct~表示使用it这个百分值保留多少Ct~的值。
  5. 3.比如遗忘门中的通过sigmiod输出的ft便是一个0和1之间的小数值，ft用作在“细胞状态更新公式”中的ft*Ct-1，
  6.   因为ft本身就是一个0和1之间的小数值(相当于一个百分比值)，那么ft*Ct-1表示使用ft这个百分值保留多少Ct-1的值。

 

  1. 1.激活函数sigmiod的作用：用于帮助调节流经网络的值, sigmoid函数将值压缩在0和1之间的小数值(相当于一个百分比值)。
  2.   只要是sigmiod输出的百分比值(比如ft/it/ot) 都可作为控制阈值(保留信息比例值)，用于控制流经的数据保留多少。
  3. 2.比如此处输出门中的通过sigmiod输出的ot便是一个0和1之间的小数值，ot用作在“输出门更新公式”中的ot*tanh(Ct)，
  4.   因为ot本身就是一个0和1之间的小数值(相当于一个百分比值)，那么ot*tanh(Ct)表示使用ot这个百分值保留多少tanh(Ct)的值。

GRU

RNN和GRU.py

  1. import torch
  2. import torch.nn as nn
  3.  
  4. #nn.RNN(输入数据的词嵌入维度, 隐藏层中神经元数量, 隐藏层层数)
  5. # rnn = nn.RNN(5, 6, 2)
  6. rnn = nn.GRU(5, 6, 2)
  7. #input输入数据，torch.randn(当前批次的样本个数, 当前样本的序列长度(单词个数), 词嵌入维度影)
  8. input = torch.randn(4, 3, 5)
  9. #hn隐藏层数据，torch.randn(隐藏层层数, 当前样本的序列长度(单词个数), 隐藏层中神经元数量)
  10. h0 = torch.randn(2, 3, 6)
  11. """
  12. nn.GRU 和 nn.LSTM 和 nn.RNN中，output是hn隐藏层中的最后一层输出，有如下情况：
  13.     1.当前批量数据只有一个样本的情况：
  14.         1.当隐藏层只有一层时，rnn的输出output和隐藏层数据hn 两者完全相同，shape均为[1,3,6]。
  15.           比如output的shape均为[1,3,6]，[1,3,6]中的1表示一个样本，3表示样本的序列长度(单词个数)，6表示隐藏层中神经元数量。
  16.         2.当隐藏层有多层时，rnn的输出output实际为多层隐藏层数据hn中的最后一层数据。
  17.           比如隐藏层有4层，那么hn为[4,3,6]，output为[1,3,6]，hn的[4,3,6]中的4表示4层的隐藏层数据，
  18.           output的[1,3,6]实际为4层隐藏层中最后一层隐藏层的数据，即output的[1,3,6]中的[3,6]实际和hn中最后一个二维矩阵数据相同。
  19.     2.当前批量数据有多个样本的情况：
  20.         1.当隐藏层只有一层，批量数据有4个样本时，比如output.shape为[4, 3, 6]，hn.shape为[1, 3, 6]，
  21.           output的[4, 3, 6]中的4表示4个样本的输出数据，hn的[1, 3, 6]实际是批量数据样本中最后一个样本的输出数据，
  22.           即hn的[1, 3, 6]中的[3,6]实际和output中最后一个二维矩阵数据相同。
  23.         2.当隐藏层有多层时，比如有2层隐藏层，批量数据有4个样本时，output.shape为[4, 3, 6]，hn.shape为[2, 3, 6]。
  24.           output的[4, 3, 6]中的4表示4个样本的输出数据，hn的[2, 3, 6]中的2表示2层隐藏层数据，
  25.           只有output中的最后一个二维矩阵和hn中的最后一个二维矩阵相同，因为output是hn隐藏层中的最后一层输出的关系，
  26.           那么批量样本输出数据output中最后一个样本的输出数据和hn隐藏层中的最后一层的隐藏层数据相同。
  27. """
  28. output, hn = rnn(input, h0)
  29.  
  30. print("output.shape",output.shape)
  31. print("hn.shape",hn.shape)
  32. print("output",output)
  33. print("hn",hn)

LSTM.py

  1. import torch.nn as nn
  2. import torch
  3. #nn.LSTM(输入数据的词嵌入维度, 隐藏层中神经元数量, 隐藏层层数)
  4. rnn = nn.LSTM(5, 6, 2)
  5. #input输入数据，torch.randn(当前批次的样本个数, 当前样本的序列长度(单词个数), 词嵌入维度影)
  6. input = torch.randn(4, 3, 5)
  7. #hn隐藏层数据，torch.randn(隐藏层层数, 当前样本的序列长度(单词个数), 隐藏层中神经元数量)
  8. h0 = torch.randn(2, 3, 6)
  9. #cn细胞状态数据，torch.randn(隐藏层层数, 当前样本的序列长度(单词个数), 隐藏层中神经元数量)
  10. c0 = torch.randn(2, 3, 6)
  11.  
  12. """
  13. nn.GRU 和 nn.LSTM 和 nn.RNN中，output是hn隐藏层中的最后一层输出，有如下情况：
  14.     1.当前批量数据只有一个样本的情况：
  15.         1.当隐藏层只有一层时，rnn的输出output和隐藏层数据hn 两者完全相同，shape均为[1,3,6]。
  16.           比如output的shape均为[1,3,6]，[1,3,6]中的1表示一个样本，3表示样本的序列长度(单词个数)，6表示隐藏层中神经元数量。
  17.         2.当隐藏层有多层时，rnn的输出output实际为多层隐藏层数据hn中的最后一层数据。
  18.           比如隐藏层有4层，那么hn为[4,3,6]，output为[1,3,6]，hn的[4,3,6]中的4表示4层的隐藏层数据，
  19.           output的[1,3,6]实际为4层隐藏层中最后一层隐藏层的数据，即output的[1,3,6]中的[3,6]实际和hn中最后一个二维矩阵数据相同。
  20.     2.当前批量数据有多个样本的情况：
  21.         1.当隐藏层只有一层，批量数据有4个样本时，比如output.shape为[4, 3, 6]，hn.shape为[1, 3, 6]，
  22.           output的[4, 3, 6]中的4表示4个样本的输出数据，hn的[1, 3, 6]实际是批量数据样本中最后一个样本的输出数据，
  23.           即hn的[1, 3, 6]中的[3,6]实际和output中最后一个二维矩阵数据相同。
  24.         2.当隐藏层有多层时，比如有2层隐藏层，批量数据有4个样本时，output.shape为[4, 3, 6]，hn.shape为[2, 3, 6]。
  25.           output的[4, 3, 6]中的4表示4个样本的输出数据，hn的[2, 3, 6]中的2表示2层隐藏层数据，
  26.           只有output中的最后一个二维矩阵和hn中的最后一个二维矩阵相同，因为output是hn隐藏层中的最后一层输出的关系，
  27.           那么批量样本输出数据output中最后一个样本的输出数据和hn隐藏层中的最后一层的隐藏层数据相同。
  28. """
  29. output, (hn, cn) = rnn(input, (h0, c0))
  30.  
  31. print("output.shape",output.shape)
  32. print("hn.shape",hn.shape)
  33. print("cn.shape",cn.shape)
  34. print("output",output)
  35. print("hn",hn)
  36. print("cn",cn)
  37.

本文内容由网友自发贡献，转载请注明出处：【wpsshop博客】
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号