SCI一区 | Matlab实现BO-CNN-BiLSTM-Mutilhead-Attention贝叶斯优化卷积神经网络-双向长短期记忆网络融合多头注意力机制多特征分类预测_贝叶斯优化cnn-bilstm

SCI一区 | Matlab实现BO-CNN-BiLSTM-Mutilhead-Attention贝叶斯优化卷积神经网络-双向长短期记忆网络融合多头注意力机制多特征分类预测

分类效果

基本介绍

1.Matlab实现BO-CNN-BiLSTM-Mutilhead-Attention贝叶斯优化卷积神经网络-双向长短期记忆网络融合多头注意力机制多特征分类预测，BO-CNN-BiLSTM-Mutilhead-Attention/Bayes-CNN-BiLSTM-Mutilhead-Attention；
MATLAB实现BO-CNN-BiLSTM-Mutilhead-Attention贝叶斯优化卷积神经网络-双向长短期记忆网络融合多头注意力机制多特征分类预测。多头自注意力层 (Multihead-Self-Attention)：Multihead-Self-Attention多头注意力机制是一种用于模型关注输入序列中不同位置相关性的机制。它通过计算每个位置与其他位置之间的注意力权重，进而对输入序列进行加权求和。注意力能够帮助模型在处理序列数据时，对不同位置的信息进行适当的加权，从而更好地捕捉序列中的关键信息。
2.数据输入15个特征，输出4个类别，main.m是主程序，其余为函数文件，无需运行；
3.贝叶斯优化参数为：学习率，隐含层节点，正则化参数；
4.可视化展示分类准确率；
5.运行环境matlab2023b及以上。

模型描述

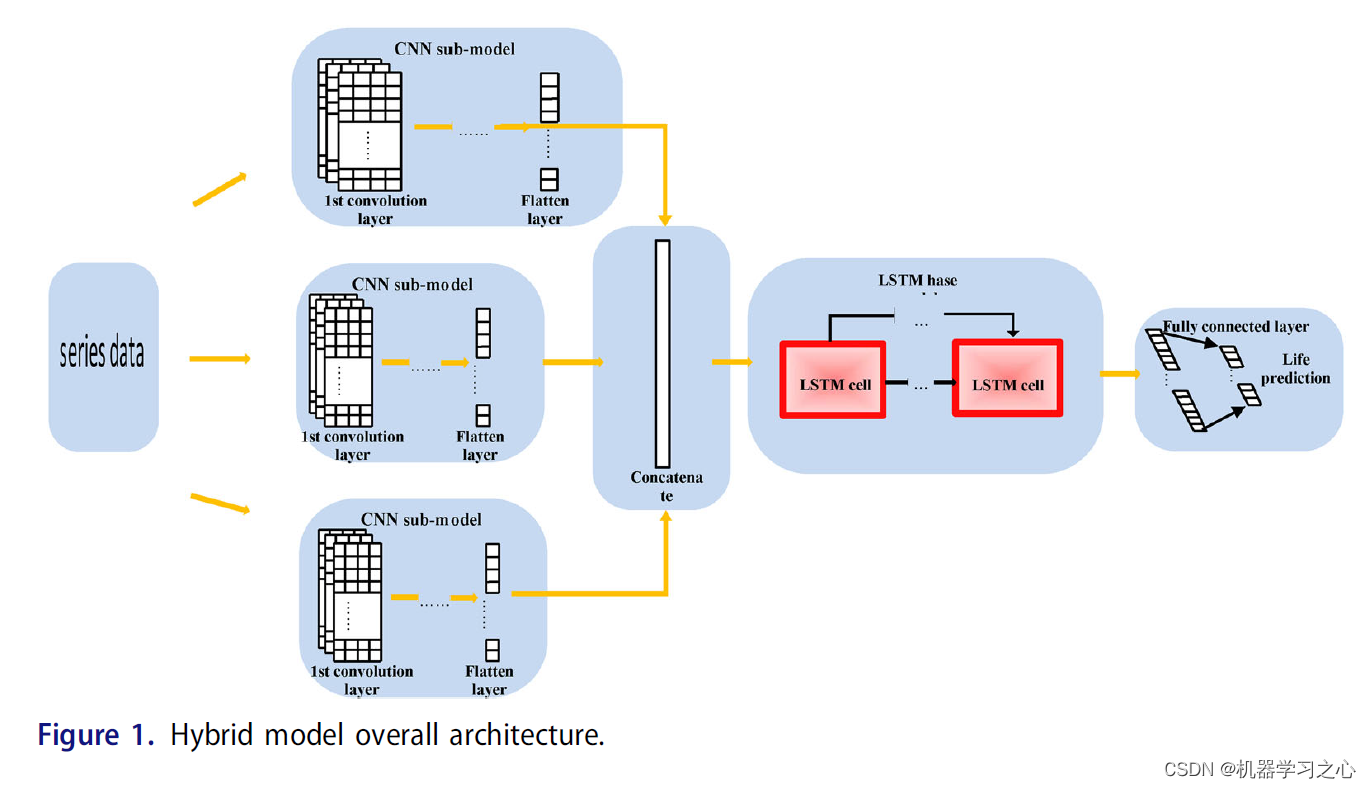
多头注意力机制（Multi-Head Attention）是一种用于处理序列数据的注意力机制的扩展形式。它通过使用多个独立的注意力头来捕捉不同方面的关注点，从而更好地捕捉序列数据中的相关性和重要性。在多变量时间序列预测中，多头注意力机制可以帮助模型对各个变量之间的关系进行建模，并从中提取有用的特征。贝叶斯优化卷积神经网络-长短期记忆网络融合多头注意力机制多变量时间序列预测模型可以更好地处理多变量时间序列数据的复杂性。它可以自动搜索最优超参数配置，并通过卷积神经网络提取局部特征，利用LSTM网络建模序列中的长期依赖关系，并借助多头注意力机制捕捉变量之间的关联性，从而提高时间序列预测的准确性和性能。

程序设计

• 完整程序和数据获取方式：私信博主回复SCI一区 | Matlab实现BO-CNN-BiLSTM-Mutilhead-Attention贝叶斯优化卷积神经网络-双向长短期记忆网络融合多头注意力机制多特征分类预测获取。

%---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%%  数据集分析
outdim = 1;                                  % 最后一列为输出
num_size = 0.7;                              % 训练集占数据集比例
num_train_s = round(num_size * num_samples); % 训练集样本个数
f_ = size(res, 2) - outdim;                  % 输入特征维度
%---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%%  划分训练集和测试集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);
%---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);
————————————————
%%  优化算法参数设置
% 参数取值上界(学习率，隐藏层节点，正则化系数)
% 卷积核大小大小
FiltZise = 10;
fitness = @fical;
%%  贝叶斯优化参数范围
optimVars = [
    optimizableVariable('NumOfUnits', [50, 100], 'Type', 'integer')
    optimizableVariable('InitialLearnRate', [1e-3, 1], 'Transform', 'log')
    optimizableVariable('L2Regularization', [1e-10, 1e-2], 'Transform', 'log')];

%%  贝叶斯优化网络参数
BayesObject = bayesopt(fitness, optimVars, ...   % 优化函数，和参数范围
        'MaxTime', Inf, ...                      % 优化时间（不限制） 
        'IsObjectiveDeterministic', false, ...
        'MaxObjectiveEvaluations', 10, ...       % 最大迭代次数
        'Verbose', 1, ...                        % 显示优化过程
        'UseParallel', false);
版权声明：本文为CSDN博主「机器学习之心」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/kjm13182345320/article/details/130471154

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

参考资料

[1] http://t.csdn.cn/pCWSp
[2] https://download.csdn.net/download/kjm13182345320/87568090?spm=1001.2014.3001.5501
[3] https://blog.csdn.net/kjm13182345320/article/details/129433463?spm=1001.2014.3001.5501