二叉树的基本运算和基本操作的接口实现（C语言）_c语言二叉树基本运算算法的实现及应用

二叉树的概念

二叉树的组成：

1. 空树
2. 非空：根节点，根节点的左子树，根节点的右子树

二叉树是递归形式的，所以接下来也是的一些基本操作都是按递归进行。

二叉树的遍历 （递归）

二叉树遍历：就是按某种特定的规则，依次对二叉树的节点进行操作。
因为前、中、后序遍历比较相似，我选一个中序遍历进行画图分析，做递归展开图。
建议：可以先观察递归展开图 ，每次函数的调用都是一次栈帧的创建，每一次函数的返回都是栈帧的销毁。

前（先）序遍历（Preorder Traversal）

定义：先访问根节点，然后访问左右子树

void PreOrder(BTNode* root)
{
	if (NULL == root)
	{
		printf("NULL ");
		return;
	}
	
	//先访问根节点，在访问左子树和右子树
	printf("%d ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13

中序遍历（Inorder Traversal）

定义：先遍历左子树，然后访问根节点，最后访问右子树

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	//先访问左子树，然后访问根节点，最后访问右子树
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);

} 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

后序遍历（Postorder Traversal）

定义：先访问左右子树，然后访问根节点。

void PostOrder(BTNode* root)
{
	if (NULL == root)
	{
		printf("NULL ");
		return;
	}

	//像=先访问左右子树，再访问根节点
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}
1
2
3
4
5
6
7
8
9
10
11
12
13

中序遍历递归展开图

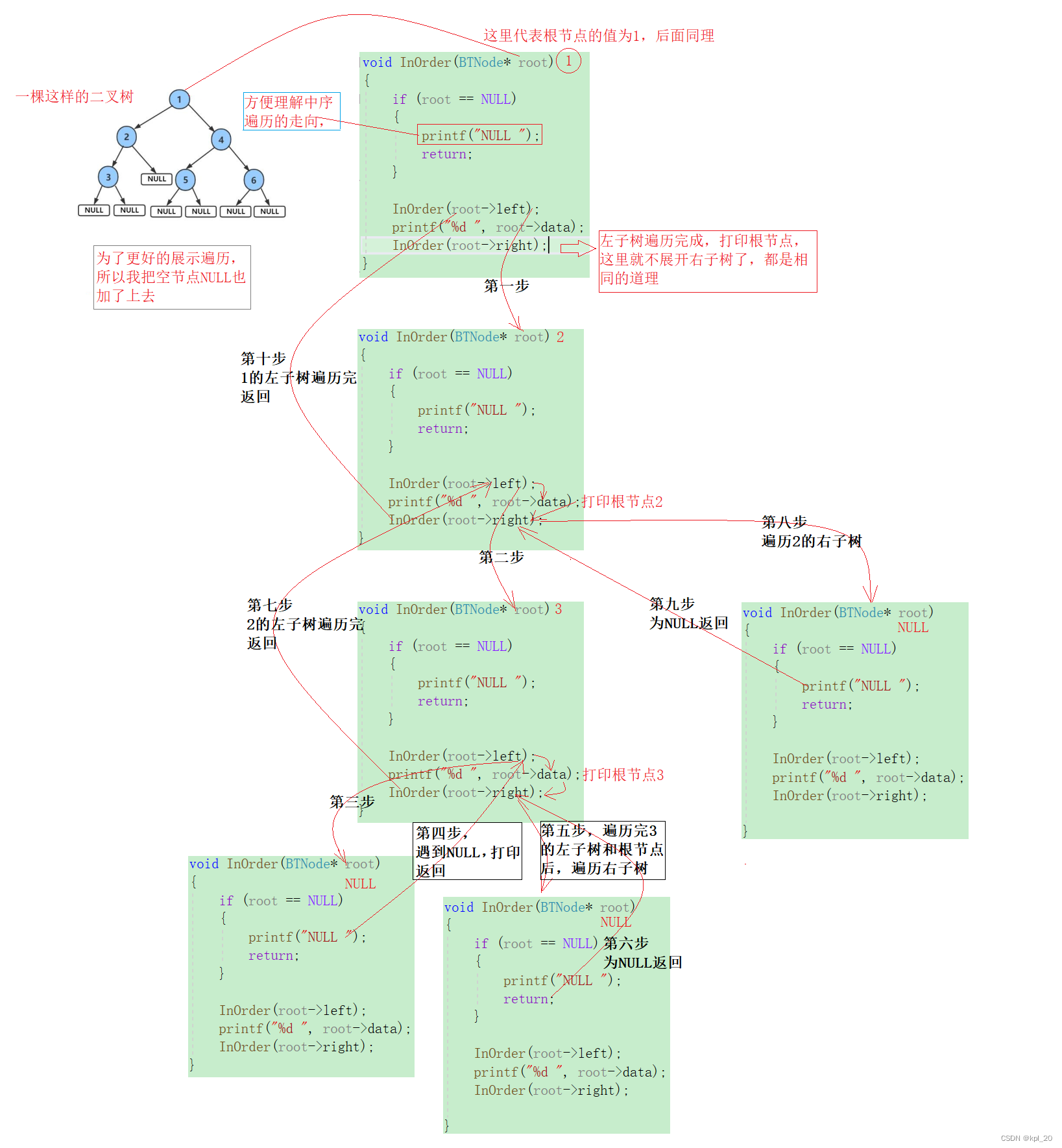
小结

1. 二叉树的遍历，都是以递归的形式实现。二叉树的遍历是很重要的运算，也是二叉树其他运算的基础。
2. 因为访问的节点一定是某子树的根。所以又称N(Node)、L(Left subtree)、R(Right subtree)。NLR:先根遍历。LNR:中根遍历。LRN:后根遍历。

二叉树的节点个数以及高度等接口的实现

选一部分接口画递归展开图。

这些基本运算都是采用分治的思想完成。分治和遍历是有区别的，我在求二叉树的节点个数接口里，会展示一次用遍历求节点个数，下面别的接口就不再展示遍历的求法了。

遍历和分治的区别

遍历通常是没有返回值的，分治是有返回值的。
遍历：通过根节点把每个节点都走个遍。
分治：分开治理，谁的孩子谁管着的原则。逻辑更清晰。

遍历：

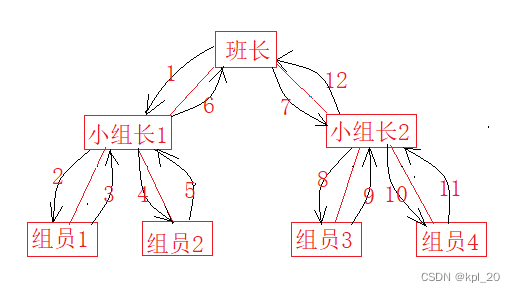
分治：

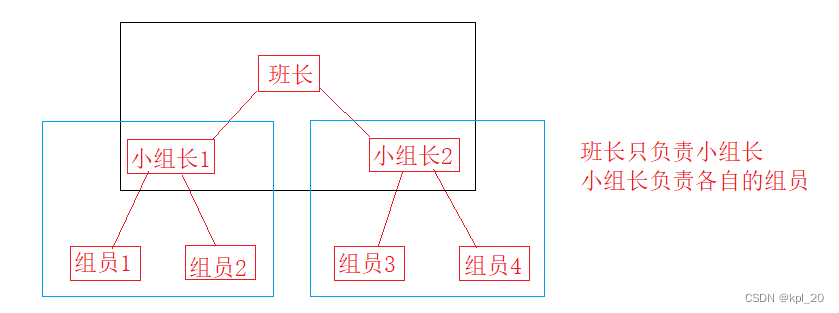
建议： 可以对照代码，在不懂的接口画递归展开图，就如同我在上面中序遍历那样，便于理解。

二叉树的节点个数

遍历

//二叉树节点个数   遍历
void BinaryTreeSize(BTNode* root, int* psize)
{
	if (NULL == root)
		return;
	//使用指针，改变数值。如果之间使用数值，可能会造成数值随着栈帧的销毁而销毁
	++(*psize);
	BinaryTreeSize(root->left, psize);
	BinaryTreeSize(root->right, psize);
}
1
2
3
4
5
6
7
8
9
10

分治

//二叉树的节点个数
int BinaryTreeSize(BTNode* root)
{
	if (NULL == root)
		return 0;
	
	//可以看我在分治和遍历的区别里介绍的分治思想的图。就如：最后一层的双亲节点（图中就是小组长），去计算下面有几个叶子节点（组员）。然后班长计算小组长汇报的情况合在一起，依次直到根节点。
	//建议画递归展开图，我在这里介绍可能还会帮读者绕进去。
	return BinaryTreeSize(root->left)
		 + BinaryTreeSize(root->right) + 1;
}
1
2
3
4
5
6
7
8
9
10
11

二叉树的高度

//二叉树的高度
int BinaryTreeHeight(BTNode* root)
{
	if (NULL == root)
		return 0;
	
	//利用好函数的返回值，既方便下次使用，又减少重复开辟栈帧的情况。
	int leftHeight = BinaryTreeHeight(root->left);
	int rightHeight = BinaryTreeHeight(root->right);
	
	//选左右子树较大的值，然后+1返回
	return leftHeight > rightHeight ? 
		   leftHeight + 1 : rightHeight + 1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

递归展开图

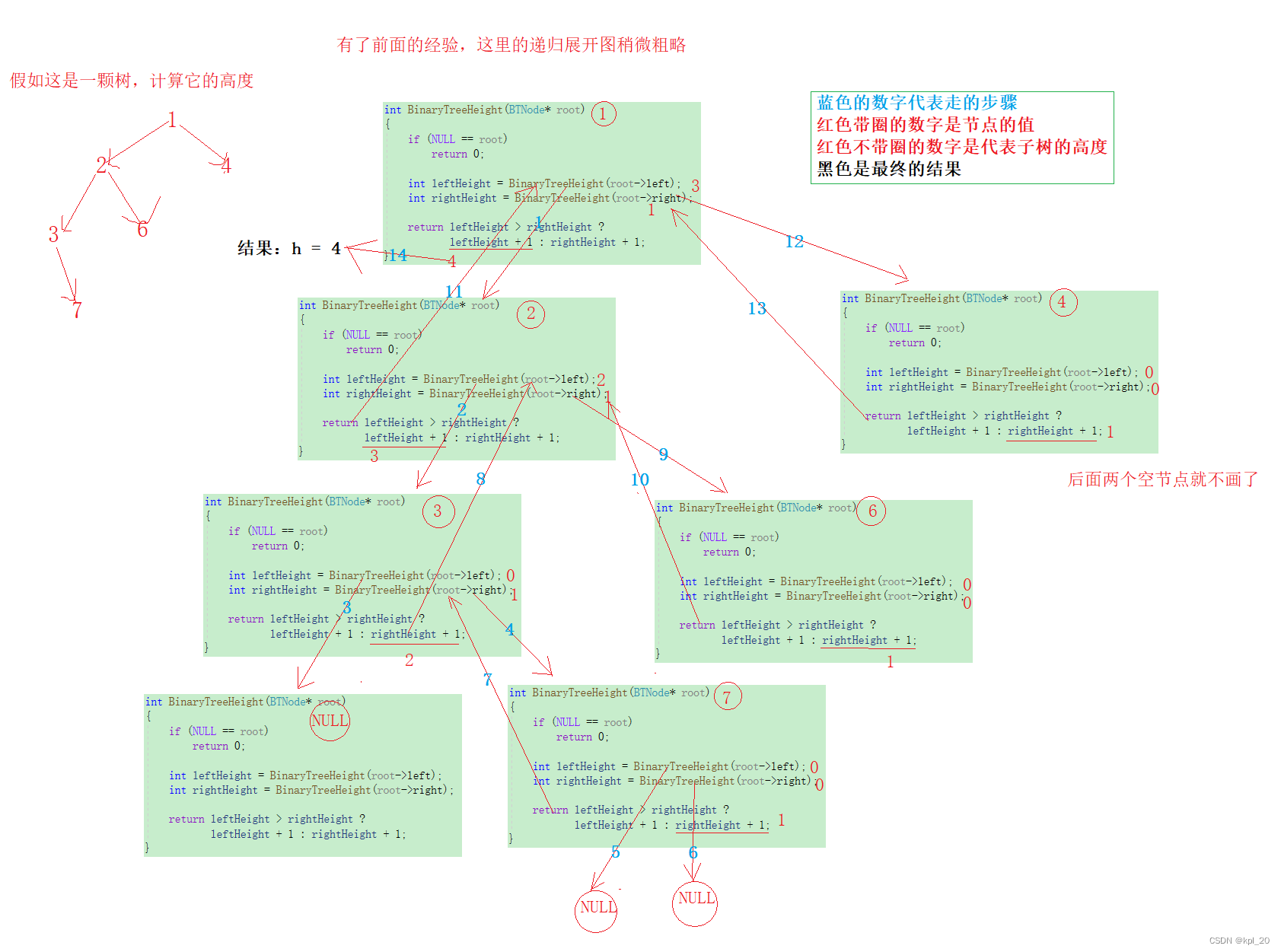
二叉树的叶子节点个数

//二叉树的叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (NULL == root)
		return 0;
		
	//判断是否为叶子节点，如果是返回1，
	if (root->left == NULL && root->right == NULL)
		return 1;

	return BinaryTreeLeafSize(root->left) 
		 + BinaryTreeLeafSize(root->right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13

二叉树的k层节点个数

//二叉树的k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	assert(k > 0);

	if (NULL == root)
		return 0;
		
	//如果不为空，能到第k层，在这里就要截停
	if (k == 1)
		return 1;
		
	//每次递归节点都要向下走一层，所以距离第k层也逐步减一。注意：递归要向递归结束的条件靠拢
	return BinaryTreeLevelKSize(root->left, k - 1)
		 + BinaryTreeLevelKSize(root->right, k - 1);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

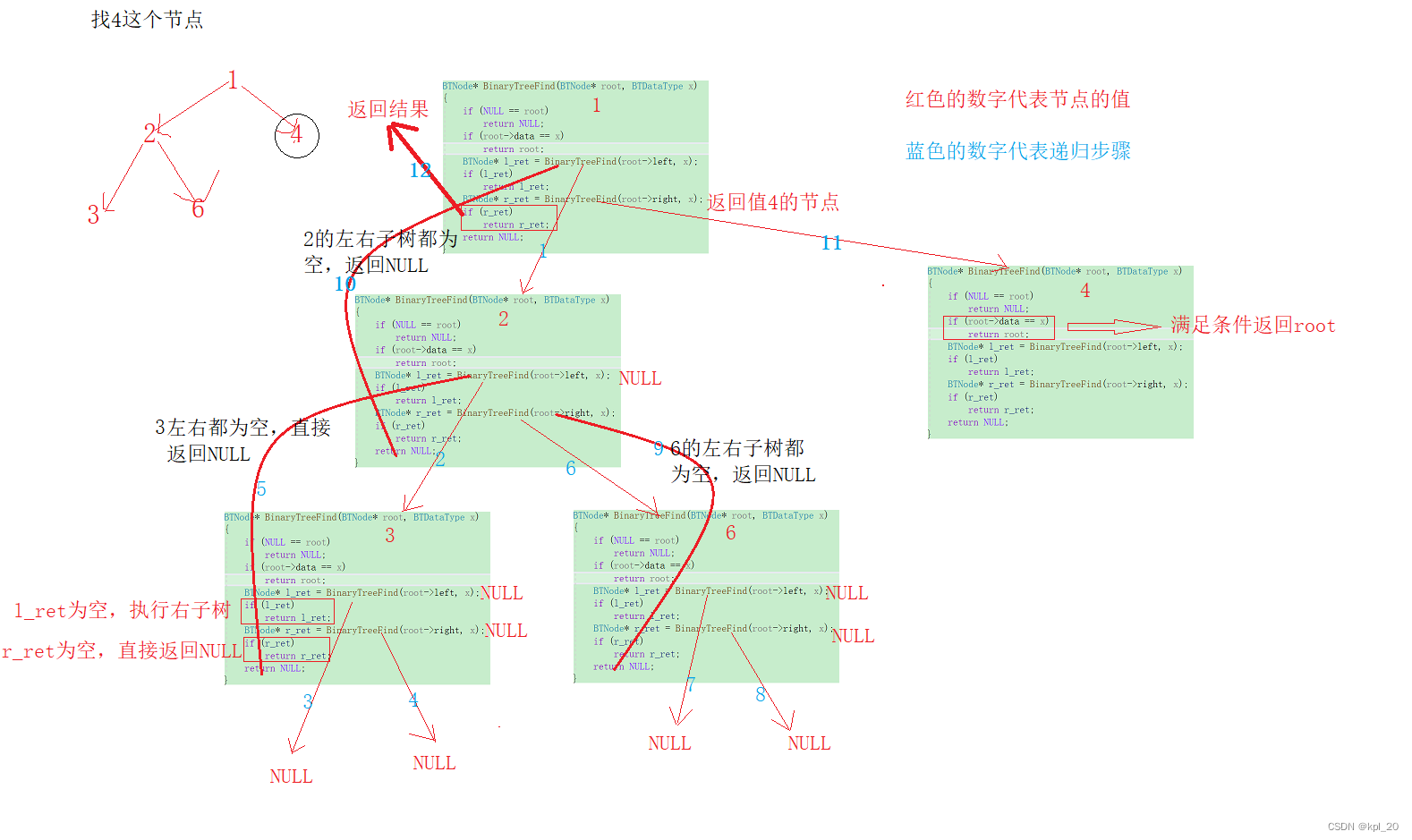
二叉树查找值为x的节点

//二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (NULL == root)
		return NULL;
		
	if (root->data == x)
		return root;

	//再次强调一下，函数的返回值一定要妥善利用
	BTNode* l_ret = BinaryTreeFind(root->left, x);
	//l_ret要么是空要么就是所要查找的节点的返回值
	if (l_ret)
		return l_ret;

	BTNode* r_ret = BinaryTreeFind(root->right, x);
	if (r_ret)
		return r_ret;

	return NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

递归展开图

二叉树的销毁

void BinaryTreeDestroy(BTNode* root)
{
    if (root == NULL)
        return 0;

	//访问左右子树，再销毁。
    BinaryTreeDestroy(root->left);
    BinaryTreeDestroy(root->right);
    free(root);
}
1
2
3
4
5
6
7
8
9
10

总结

这一块内容需要思考一下，小编在刚学的时候也有点迷茫。为什么这样做就可以计算出二叉树的节点数什么的。多画几遍递归展开图，然后思考总结。

注意： 要注意在递归的过程中函数的返回值，妥善利用。

我当初思考的时候就在想，是先有相关代码的还是先有二叉树的，两种间的联系为什么会那么巧妙。也可能是小编的脑洞太大的原因。