可扩展优化器技术的第一次努力(我们称之为第一代)开始于大约十年前，意识到需要新的数据模型、查询类、语言和计算技术。这些项目包括Exodus和StarBurst。它们的目标是让优化器更现代化和易于扩展。它们使用的技术包括层次化的组件、基于rule的transformation等等。这些工作有一些缺陷，例如扩展的复杂性、搜索效率和面向record数据模型的偏好。

可扩展优化器的第二代，例如Volcano optimizer generator，增加了更复杂的搜索技术，更多地使用物理属性来指导搜索，并更好地控制搜索策略，以实现更好地搜索性能。尽管这些优化器具有一定的灵活性，但进行扩展仍然困难而复杂。

查询优化器框架的第三代，例如Cascade、OPT++、EROC和METU，采用面向对象的设计，简化了优化器的实现、扩展和修改任务，同时保持了效率，使搜索策略更加灵活。最新一代的优化器打到了满足现代商业数据库系统需求的复杂程度。

这三代的查询优化器可以分为两类搜索策略，Starburst风格的自下而上动态规划优化器和Cascades风格的自顶向下和绑定规则驱动的基于成本的优化器。自下而上的优化器通常在传统商业数据库系统中使用，因为它被认为是有效的。但是自下而上的优化器相比自顶向下优化器缺少了扩展性，因为它要求将原始问题分解为子问题。

尽管基于之前自顶向下优化的实现表明，它们很难像自底向上的优化器那样进行性能优化，但我们相信自顶向下的优化器在效率和扩展性方面具有优势。本文其他部分描述了我们开发的一种自顶向下的优化器Columbia的尝试，以证明采用自顶向下的方法可以实现高效率。

基于Cascades Optimizer Framework的自顶向下优化，Columbia广泛利用了c++的面向对象特性，并精心设计工程师，简化了自顶向下的优化，以实现效率，同时保持可扩展性。

为了最小化CPU和内存的使用，Columbia使用了多个工程技术。包括消除重复expression的快速hash函数，group中逻辑和物理表达式的分离，小而紧凑的数据结构，优化group和input的高效算，以及处理enforcer的高效方法。

另外一个Columbia使用的重要技术是group剪枝，它极大地减少了搜索空间，同时保留了规划质量。优化器会在生成lower-level plans之前先为high-level physical plan计算cost。这些早期的cost可以作为后续优化的上界。在许多情况下，我们可以使用这些上界来避免生成整个expression group，从而在搜索空间中修剪大量可能的查询计划。

除了group剪枝，Columbia还实现了另一种剪枝技术：全局剪枝。这种技术通过生成可接受的接近最优的解来显著地修剪搜索空间。当找到一个解足够接近最优解时，优化目标就完成了，因此不需要考虑大量的表达式。对这种剪枝技术进行了分析。结果表明了优化的有效性和误差。

Chapter 2. Terminology

2.1 查询优化器

查询处理器的目的是接受用数据库系统的数据操作语言(DML)表示的请求，并根据数据库的内容对其进行评估。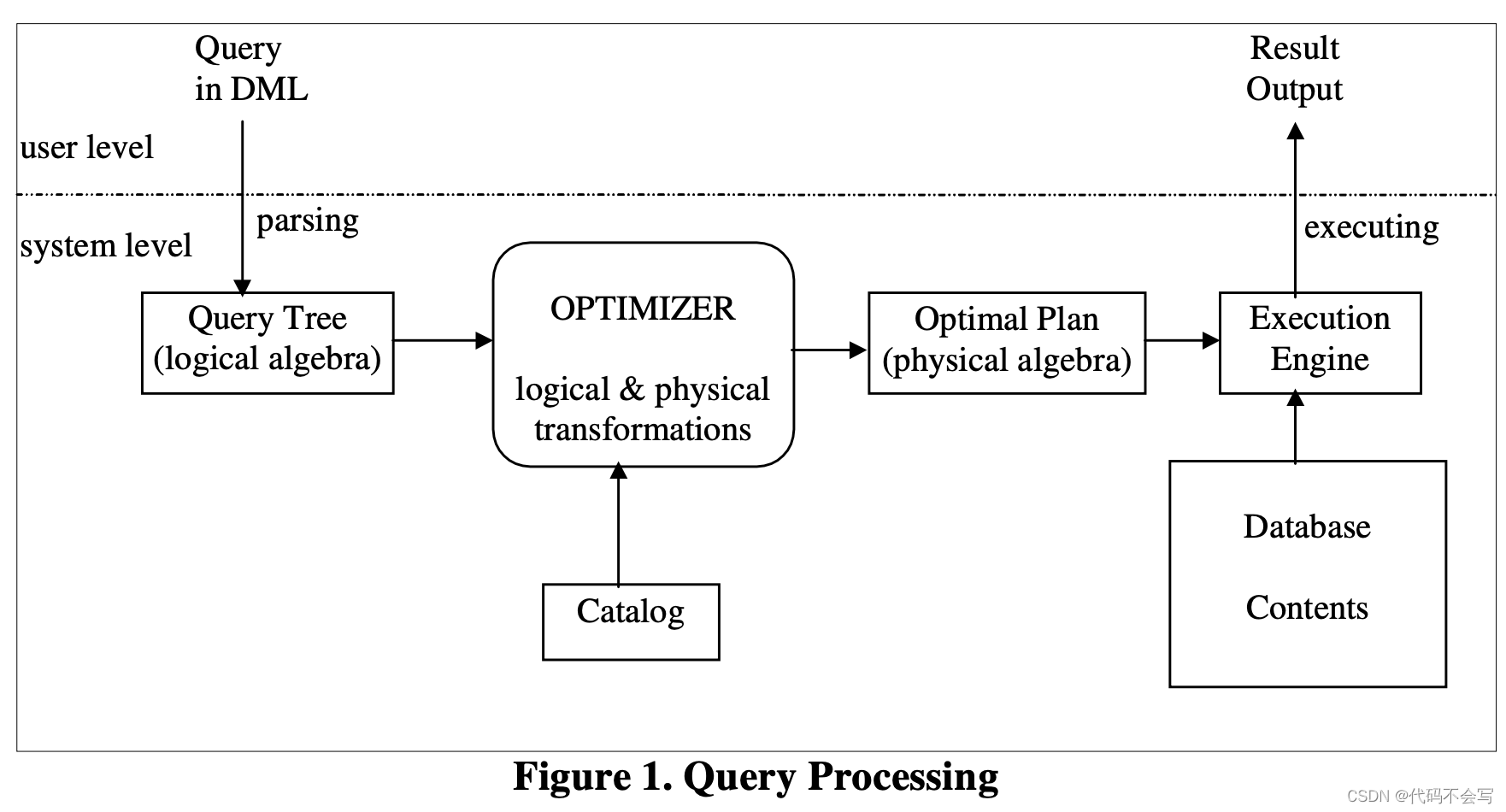

上图展示了查询处理过程中的步骤。DML语法中的原始查询被解析为逻辑代数构成的逻辑表达式树，其在后续阶段可以很容易被计算。查询的内部逻辑形式会被传递给查询优化器，它负责来将逻辑查询转换为物理查询计划，该计划会针对保存数据的物理数据结构进行执行。两种类型的transformation会被执行：

创建对查询等价的可选逻辑形式的logical transformation，例如交换树的左右子节点
和选择一种特定的物理算法来实现逻辑算子的physical transformation，例如针对join操作选择sort-merge join算法。

这个过程通常会产生大量的实现查询树的执行计划。找到最优的执行计划（相对于cost model来说，其包括了统计信息和其他catalog信息）是查询优化器的主要关注点。一旦一个最优（或是接近最优）的查询物理执行计划被选择，它就会被传递给查询执行引擎。查询执行引擎使用存储数据库作为输入来执行这个计划，并产生查询结果作为输出。

站在用户视角来看，查询处理过程是一个黑盒。用户通过high level的语言，例如SQL，Quel或是OQL，来提交查询请求到数据库系统，希望能够获得准确和快速的输出。准确性无意是一个查询处理器的绝对要求，同时性能是一个立项的特性，也是查询处理器的主要关注点。正如我们在查询处理过程的系统级别看到的一样，查询优化器一个对于高性能起作用的关键组件。对于一个查询来说，有大量的执行计划可以将它准确地执行，但是具有不同的执行性能。优化器的其中一个目标是找到具有最优执行性能的执行计划。优化器可以选择生成所有可能的执行计划并选择最优的一个。但是，探索所有可能的计划的成本非常高，因为即使是相对简单的查询，也有大量的替代计划。因此，优化器必须以某种方式缩小他们所考虑的备选方案的空间。

查询优化是一个复杂的搜索问题。研究表明，这个问题的简化版本是NP-hard。事实上，即使是最简单的关系Join，在使用动态规划时必须计算的join数量也是输入relation数量的指数关系。所以一个好的搜索策略对于优化器的成功是至关重要的。

2.2 逻辑算子和查询树

逻辑算子Logical Operator是指定了数据转换逻辑但不需要指定物理执行算法的high-level operators。在关系模型中，logical operators通常接收tables作为输入，并产生1个单独的table作为输出。每个logical operator都会接收指定数量的input（我们称之为operator的参数数量arity），并且可以会有一些能够区分operator变体的参数。

两种典型的logical operators是GET和EQJOIN。GET operator没有input，只有一个参数，即为存储relation的名称。GET从磁盘检索relation的元组并将这些元组输出给后续的operations。EQJOIN operator有2个input，即需要执行join的left和right table，以及一个参数，它是一组与左表和右表相关的连接谓词。

查询树query tree是一个代表了整个查询，并作为优化器输入的树形结构。通产来说一个query tree以一个logical operators的属性结构表示，其中每个节点是一个logical operator，有0个或多个logical operators作为它的输入。节点的子节点数量就是operator的参数数量arity。query tree用来执行operator的执行顺序。

2.3 物理算子和执行计划

物理算子Physical Operator代表着实现特定数据库操作的指定算法。一个或多个物理执行算法可以在一个数据库之上执行来实现一个给定的query logical operator。例如，EQJOIN operator可以使用nested-loop或是sort-merge或是其他算法来实现。这些特定的算法可以在不同的physical operator中实现。和logical operator一样，每一个physical operator也都有固定数量的input（即operator的参数数量arity），以及可能存在的参数。

将query tree中的logical operator替换为能够实现它们的physical operator，将产生一棵physical operator tree，对于给定查询，这被称为执行计划Execution Plan或访问计划access plan。图3显示了与图2(b)中的查询树相对应的两种可能的执行计划。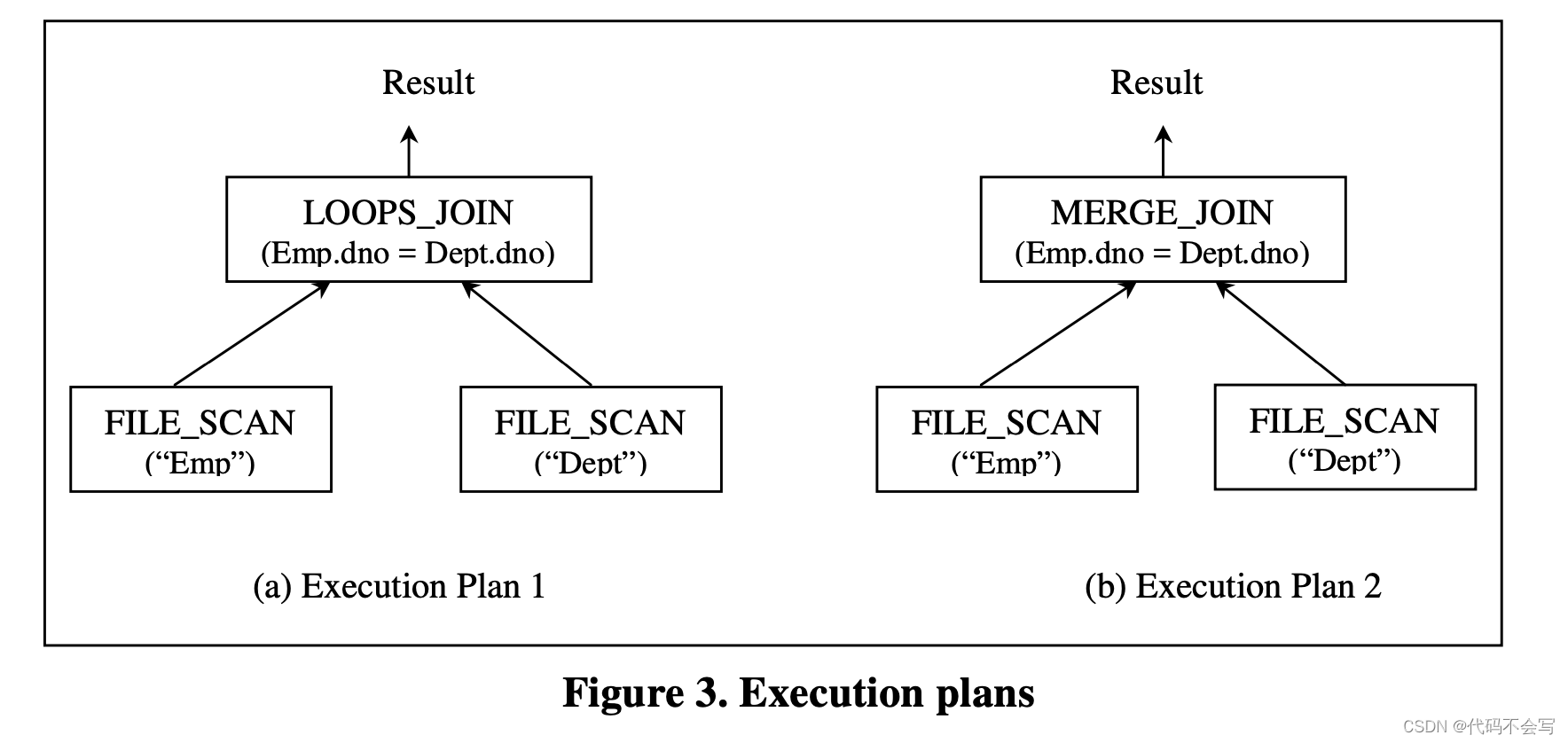

Execution plan指定了查询的评估方式。每一个执行计划都有一个与cost model和catalog信息对应的执行cost。通常来说，优化器会为一个给定查询生成一个好的执行计划，并作为查询执行引擎Query Execution Engine的输入，查询执行引擎会根据数据库系统的数据来执行整体的算法，易产生给定查询的输出结果。

2.4 Groups

一个给定的查询可以通过逻辑等价的一个或其他的query treee表达。如果两个query tree对于数据库的任意输出产生完全相同的结果，那我们就称它们是逻辑等价logicall equivalent的。对任意的query tree，通常来说都会有一个或多个实现该query tree并产生严格一致结果的execution plan。同样，这些执行计划execution plan也可以成为是逻辑等价的。下图展示了几个逻辑等价的query tree和execution plan。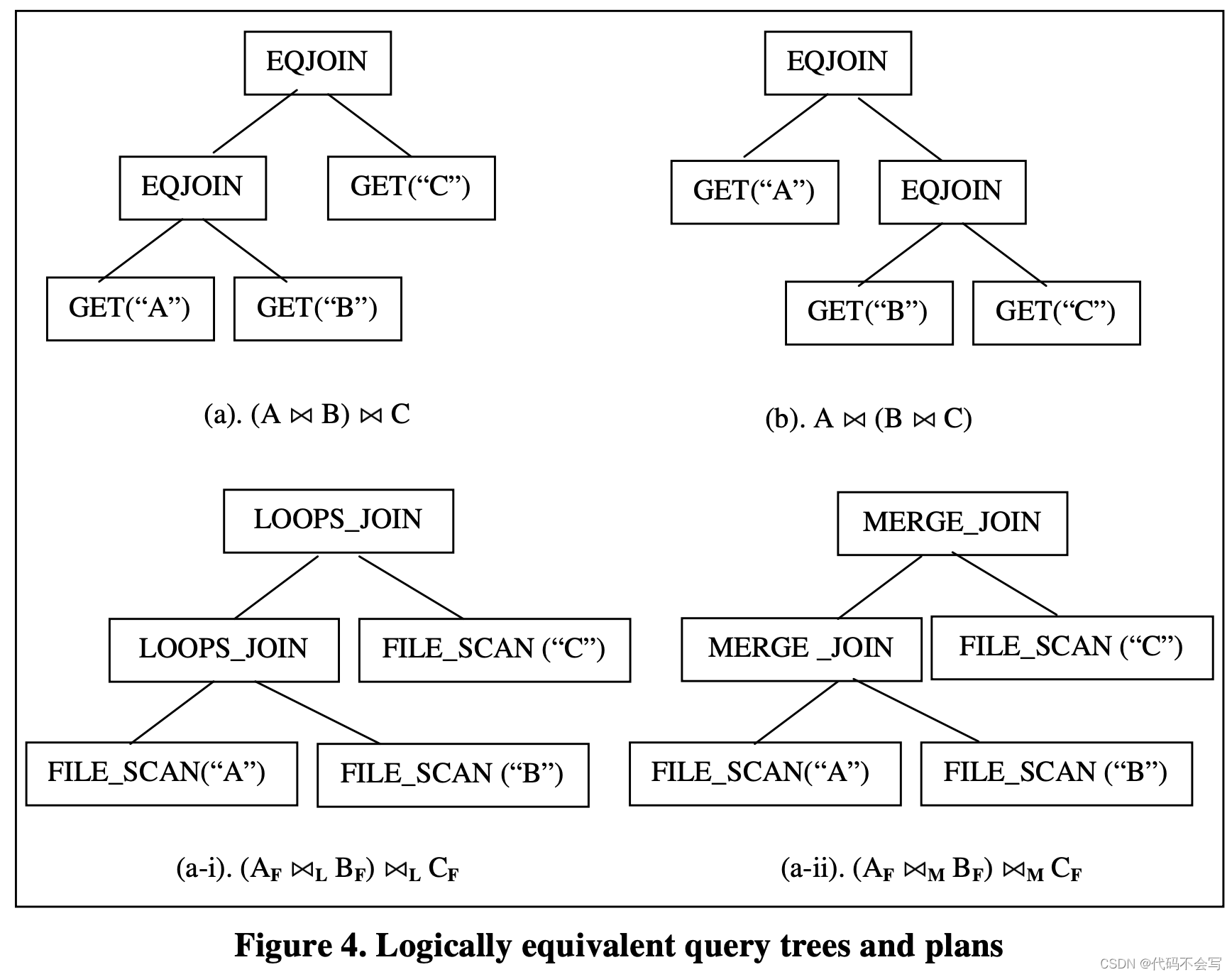

我们可以使用表达式expression来代表query tree和execution plans（或是sub trees和sub plans）。一个expression由一个operator和零个或一个input expression组成。根据operator的类型，我们将expression称为logical expression或physical expression。因此，query tree是logical plan，而execution plan是physical expression。

给定一个logical expression，它会有一系列的逻辑等价的logical和physical expressions。将它们收集到group中并定义公共的属性是非常有用的。一个Group就是一组逻辑等价的expression。通常来说，一个group会包含一个expression的所有等价的logical形式，以及这些logical形式对应的可选的physical expression。通常，一个group的每个logical expression都有不止一个physical expression。下图展示了一个包含Figure 4中的expression及其的等价expression。

为了减少一个group中的expression数量，Multi-expressions被引入了。一个Multi-expression由一个logical或是physical operator组成，并接收group作为input。Multi-expression和expression是一样的，除了它的input是group，而expression的input是其他expression。Multi-expression的优势在于，它极大地节省了空间，因为一个group中的等价multi-expression会更少。下图为group[ABC]对应的等价multi-expression。和Figure 5相比，group中的multi-expression少了。事实上，一个multi-expression通过获取group作为input可以代表多种不同的expression。

在典型的查询处理中，在产生最终结果钱会产生许多中间结果（元组的组合）。一个中间结果是通过计算一个group中的execution plan（或physical plan）产生的。在这个意义上，group对应于中间结果（这些group被称为intermediate group）。只会有一个最终结果，对应的group被称为final group。

一个group中的Logical properties被定义为结果的逻辑属性，而不管这个结果是如何物理计算和组织的。这些属性包括cardinality（元组的数量）、schema和其他属性。Logical properties作用于一个group中的所有expression

2.3 搜索空间

搜索空间search space代表对于一个给定初始化查询的logical query tree和physical plans。为了节省空间，search space使用一组group来表示，每个group接收一些group作为input。有一个top group会被执行为final group，对应于初始查询的最终评估结果。下图展示了给定查询的initial search space。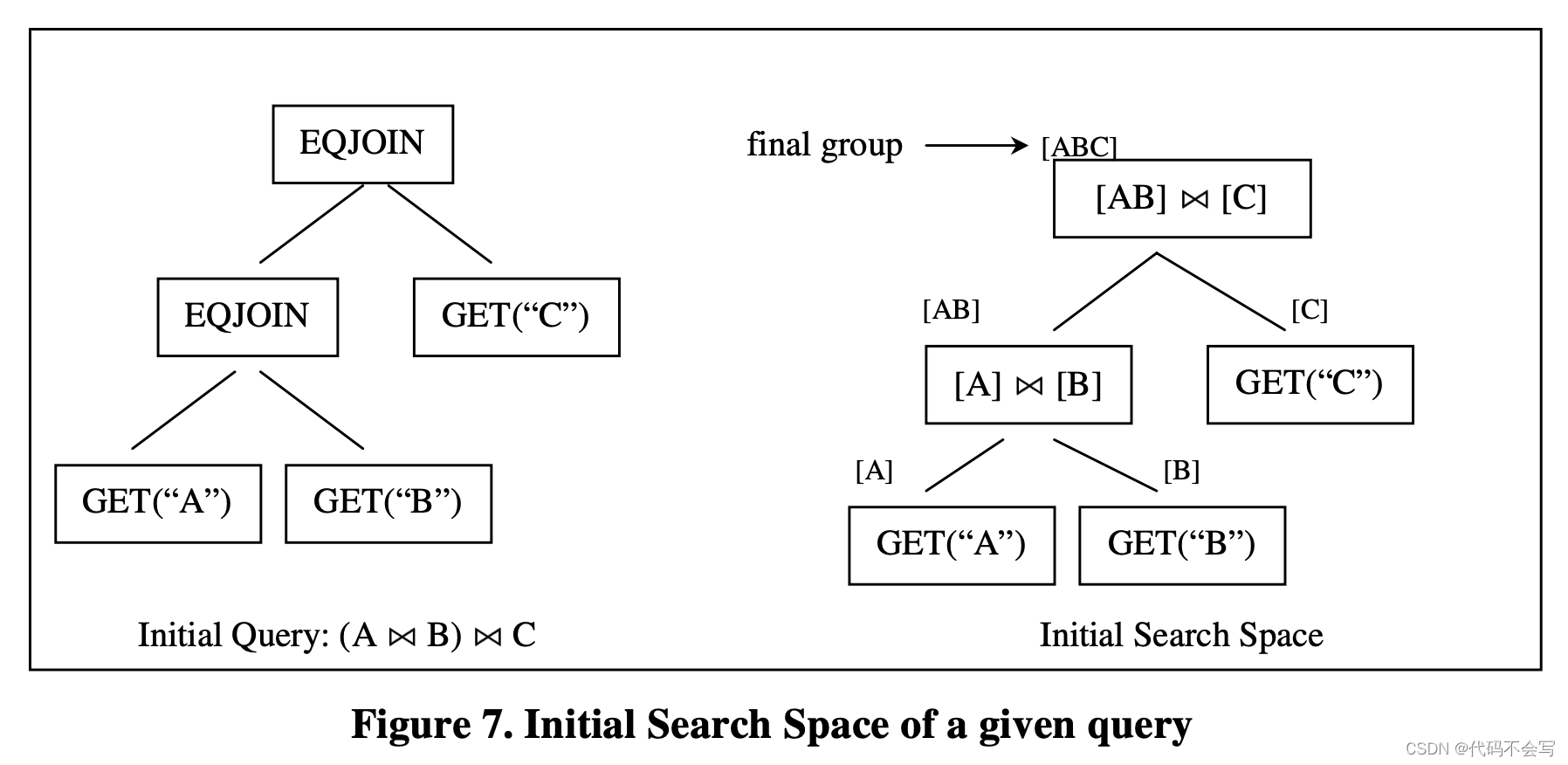

在initial search space中，每个group只包含一个logical expression，来源于初始的query tree。在上图中，group[ABC]，就是查询的final group。它对应于3个relation join的最终结果。我们可以从initial search space中导出initial query tree。Query tree中的每一个节点对应着search space中每个group中的一个multi-expression。

在优化过程中，每个group中的逻辑等价logical和physical expressions会被生成，极大地扩展了搜索空间。每个group会有大量的logical和physical expressions。在优化生产physical expression的同时，physical expression的执行cost会被计算出来。从某种意义上来说，生成所有的physical expressions是优化目标，因为我们想要找到最优的执行计划，而且我们知道cost只和physical expression相关。但是为了生成所有的physical expression，就必须生成所有的logical expression，因为physical expression是logical expression的物理实现。

在完成优化过程，即为每一个group生成了所有的等价physical expressions，并且所有可能的execution plan的cost都被计算完成后，最优的execution plan可以在search space中被定为并作为优化器的输出。一个完全扩展的search space被称为final search space。通常，一个final search space代表了给定查询的所有逻辑等价的expressions（包括loigcal和physical的）。在final search space中我们可以通过递归的方法提取出所有可能的query tree。

但潜在query tree的数量是会随着执行计划节点的增长指数增长的，下表展示了一个具有n个relation的join的完全逻辑search space的复杂度，还只是考虑logical expressions的复杂度。假设在search space中有N个loigcal expressions，并且该数据库系统中M个join 算法，那么最终搜索空间会有M*N个physical expressions.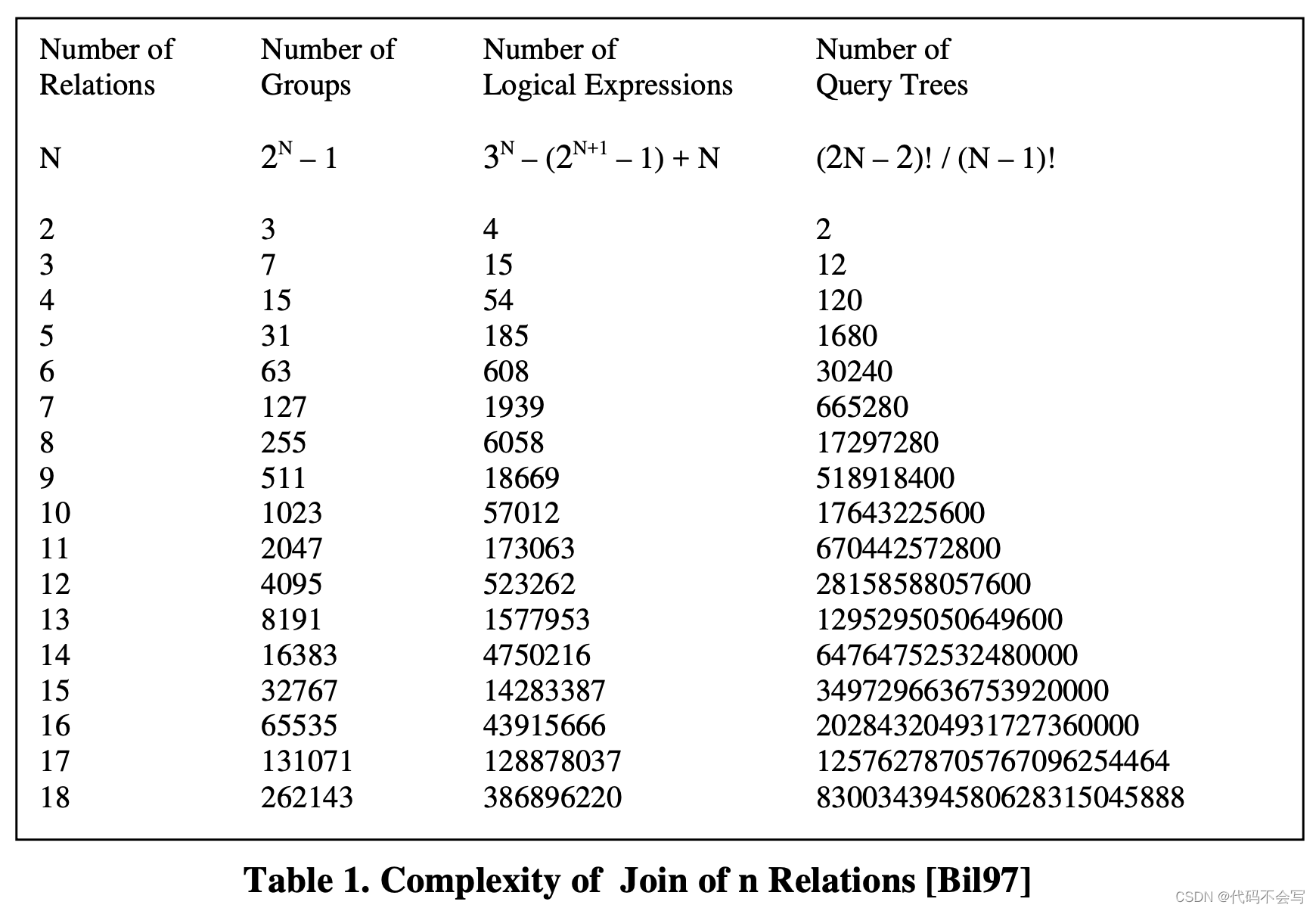

2.6 规则

许多优化器使用规则rules来生成一个给定初始查询的逻辑等价expression。一个Rule描述了如何从一个expression转换为一个逻辑等价expression。当一个Rule作用于一个给定的expression时就会产生一个新的expression。优化器会使用这些rule来扩展initial search space并基于给定的初始化查询来生成所有的逻辑等价expression。

每个rule会定义一对pattern和substitute。Pattern定义了可以应用这个rule作用的logical expression的结构。Substitute定义了在应用这个rule之后产生结果的结构。在扩展search space时，优化器会查看每一个logical expression，（注意rule不仅仅只作用于logical expression），并检查这个expression是否和rule set中的rules的任一Pattern匹配。如果一个rule的Pattern匹配上了，这个rule就会被处罚，根据rule的Substitute来生成新的逻辑等价expression。

Cascades使用expression来表示Pattern和Substitute。Pattern始终都是logical expression，但Substitute可以是logical expression或是physical expression。Transformation rules和Implementation rule是两种常见的rule类型。如果一个Rule的Substitute是logical expression，那么它被称作transformation rule。如果一个Rule的Substitute是physical expression，那么它被称为Implementation rule。这两种rule的示例如下图：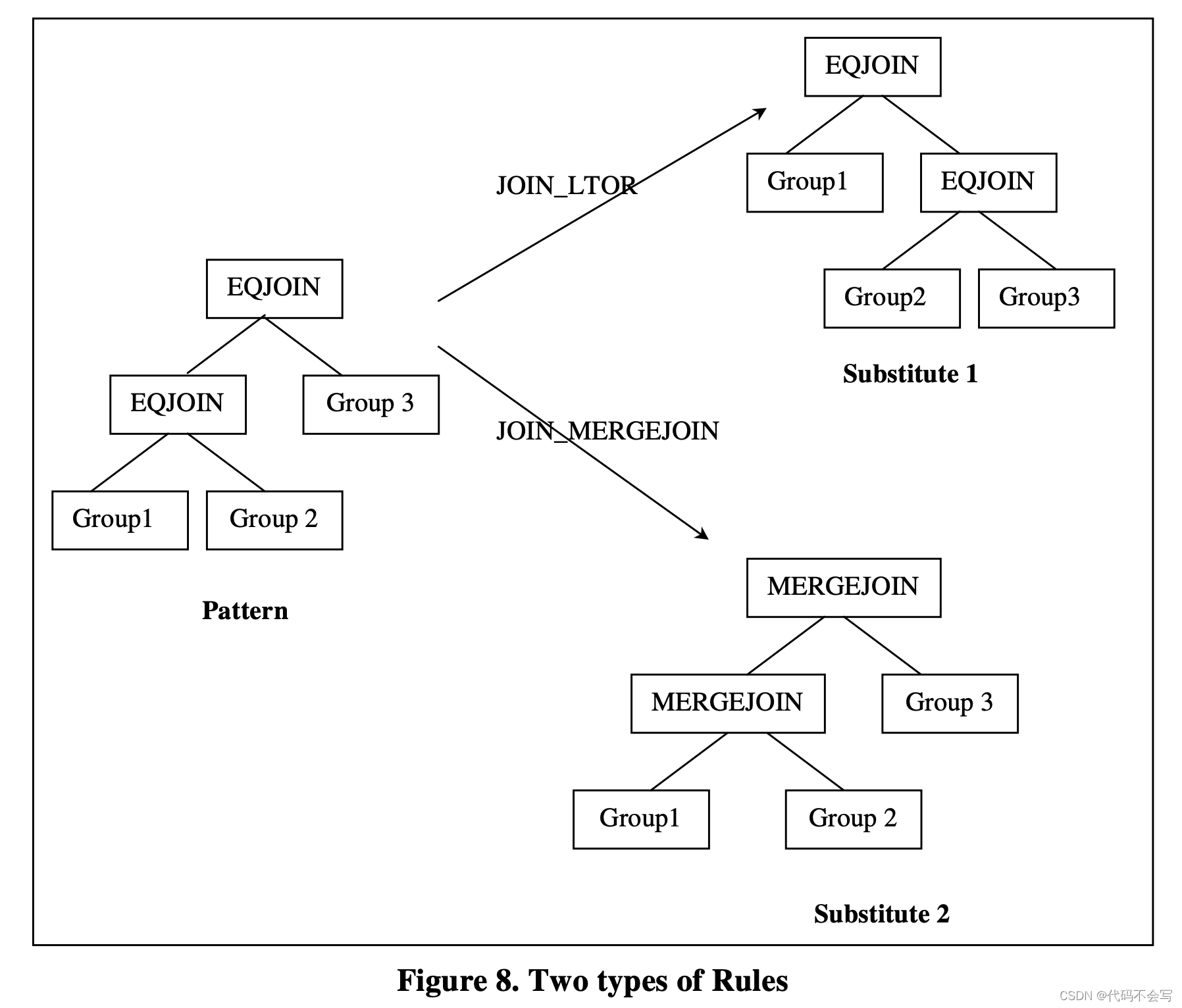

Chapter 3. Related Work

查询优化的开创性工作可以追溯到二十年前。IBM的System R优化器[SAC+79]取得了成功，并且工作得非常好，它已经成为当前许多商业优化器的基础。

数据库系统和应用程序不断发展，需要新一代的优化器来处理数据库系统的新扩展。关系数据模型扩展了更多的特性，比如支持新的数据类型和新的操作。引入面向对象的数据模型是为了处理更复杂的数据。由于早期的优化器被设计为与相对简单的关系数据模型一起使用，因此开发了新一代的可扩展优化器来满足不断发展的数据库系统的需求。新一代的优化器关注可扩展性以及所有优化器的困难目标:效率。本章将介绍一些对查询优化文献有重大贡献的著名优化器。

3.1 System R和Starburst优化器

System R优化器的一个重要的贡献是cost-based optimization。优化器使用存储在系统catalog中的relation和index的统计信息来确定一个查询评估计划的cost。cost估算分为两部分：一是对operator cost的估算。另一个是估计查询块结果的大小，以及是否对其排序。

对operator cost的估算要求获取input relation的多种参数，例如cardinality（relation的size），page的数量和可用的index。这些统计信息保留在DBMS system catalog中。size估算在cost估算中拌验证重要的角色，因为一个operator的output可以是另一个operator的input，并且operator的cost依赖于input的size。System R定义了一系列的size评估公式，这些公式在现在的查询优化器中仍然使用着，尽管近年来已经提出了基于更详细的统计数据的更复杂的技术(例如，系统值的直方图)。

System R优化器的另外一个重要的贡献是bottom-up动态规划搜索策略。动态规划的思想是在query tree中找到底层query block中的最优计划（query block概念对应于Cascade/Columnbia中的group），并只保留这些最优方案给上层的query block。它是一种自底向上的样式，因为它总是首先优化较低级的expression。为了计算上层expression的成本，必须计算其下层输入(也包括expression)的所有成本(以及结果的大小)。动态规划的技巧是：在我们优化了一个query block后（eg. 我们找到一个最优计划），我们会将这个query block的所有等价表达式都丢弃，只保留这个query block的最后计划。动态规划需要考虑O(3^N)个expressions（plan），其计算复杂度是一个指数增长的方式。当N比较大时，优化器需要考虑的expression的数量是不可接受的。因此System R优化器同时也使用了启发式heuristics的方法，例如将笛卡尔积相关的优化延迟到最终处理，或者是在优化大型查询时只考虑左深树（排除了大量的query tree，例如bushy tree）。但是，排除笛卡尔积或是只考虑左深树可能会被迫选择一个糟糕的方案，因此不能保证最优。

IBM的Starburst优化器[HCL90]使用可扩展的、更有效的方法扩展了System R优化器。Starburst由两个基于rule的子系统组成：查询重写或是查询图模型（Query Graph Model, QGM）优化器和plan优化器。QGM是查询的内部语义表示。QGM使用一组生产规则来以启发式的方式将QGM转换为一个语法等价的“更优”的QGM。这个阶段的目的是简化和改进消除冗余，并推导出更容易让计划优化器以基于成本的方式进行优化的表达式。plan优化器是一个select-project-join优化器，它由一个join枚举器和一个plan生成器组成。join枚举器使用两种连接可行性标准(强制和启发式)来限制连接的数量。join枚举器算法不是基于规则的，是用C语言编写的，并且它的模块设置允许它被其他可选的枚举算法替代。plan生成器使用类似于语法的生产规则来为join构造访问计划。这些参数化的生产规则被称为战略替代规则（Strategic Alternative Rules, STARs）。STARs可以决定那个table是inner，哪个是outer，要考虑哪些join方法等等。

在Starburst中，查询优化是一个两阶段处理。在第一个阶段，一个用QGM表达的初始化查询被传递给QGM优化器并被重写为一个“更优”的QGM。新的QGM被传递给plan优化器。在第二个阶段，plan优化器和QGM优化器通信并产生访问路径，并使用类似于System R优化器的bottom up的方法构建出一个最优的execution plan。

QGM优化器能够进行复杂的启发式优化。因此，它有助于Starburst优化器的效率。但是，启发式有时会做出错误的决定，因为它们只依赖于逻辑信息，即，不依赖于cost估计。此外，启发式很难扩展到更复杂的包含非关系算子的复杂查询。显然，基于语法和rule的方法转换QGM和plans有助于扩展查询优化，但如何使用这种方法来优化包含非关系算子和的查询和复杂转换还是未知的。

3.2 Exodus和Volcano优化生成器

Exodus优化生成器是第一个使用top-down优化方法的可扩展优化器框架。Exodus的目标是为最小化数据模型的查询优化建立一个基础设施和工具。Exodus的输入是一个模型描述文件，它描述了一组operators、一组在构建和比较访问路径时需要考虑的方法、transformation rules（定义了query tree的transformation）和implementation rules（定义了operators和methods之间的对应关系）。为了给新的数据模型实现一个查询优化器，DBI（数据库实现者）编写了一个模型描述文件和一组C过程。生成器将模型文件转换一个编译并链接到一组C过程的C程序，以生成一个特定于数据模型的优化器。生成的优化器会一步一步地转换初始的query tree，在一个名称MESH的数据结构中维护迄今为止探索的所有替代方案的信息。在优化过程中的任意时间都会有一组可能的下一步transformation，它们被存储在一个队列结构中，称为OPEN。但OPEN非空的时候，优化器会从OPEN中选择一个transformation，将它应用到MESH中的准确的节点上，为新节点执行cost估计并将新的可用transformation加入到OPEN中。

Exodus的主要贡献是top-down优化生成器框架，它将优化器的搜索策略和数据模型进行了分离，并且将transformation rule和logical operators与implementation rule和physical operators分离了出来。尽管构造高效的优化器很困难，但它为下一代可扩展优化器提供了有用的基础。

Volcano优化生成器的主要目标是提高出Exodus的效率，旨在实现更高的效率，进一步的可扩展性和有效性。该算法将动态规划与基于physical properties的定向搜索、branch-and-bound剪枝和heuristic引导相结合，形成了一种新的定向动态规划搜索算法（directed dynamic programming），从而提高了搜索效率。Volcano中的搜索策略是top-down的、面向目标的控制策略：子expression只有在必要时才会优化。也就是说，只有那些真正参与有希望的更大plan的expression和plans才会被考虑用于优化。它也使用动态编程来存储了所有最优的子plans和优化失败，直到查询完全优化。由于使用physical properties（System R中的"interesting properties"的泛化）是非常目标导向的，并且只会提取出那些有意义的expression和plans，因此这个搜索算法是非常高效的。Volcano通过基于数据模型规范生成优化器源代码，并将cost、logical properties和physical properties封装到抽象的数据类型中，实现了更多的扩展性。通过允许穷举搜索实现了有效性，它只在优化器实现者的判断下进行修剪。

Volcano搜索策略的效率允许生成真正的优化器，作用于面向对象的数据库系统，用于具有许多规则的原型科学数据库系统。

3.3 Cascades优化器框架

Cascades优化器框架是一个可扩展的查询优化器框架，它解决了许多Exodus和Volcano优化生成器的缺点。在不放弃可扩展性、动态编程和记忆化的前提下，它在功能、易用性和健壮性方面比之前的版本有了实质性的改进。

Cascades优化器有以下优点：

优化任务的抽象，作为数据结构
Rules对象化
防止属性enforcers，例如sort operation的操作抽象为rule
根据promise对行为排序
谓词operator可以同时是logical和physical的
定义了DBI-optimizer接口的抽象接口类，以及允许DBI自定义子类层次结构
C++编写的鲁棒性更强的代码，以及充分利用C++抽象机制的clean interface
广泛的跟踪支持和更好的文档来帮助DBI

在Cascades中，优化算法被拆分为多个部分，我们称之为“tasks”。Task被当做对象实现，它们拥有一个“perform”方法定义。所有这样的task对象会在一个task结构中汇总，该task结构以一个Last-In-First-Out stack的形式实现。调度一个task和调用一个function特别相似：task从stack中弹出，它的“perform”方法被调用。在优化过程中的任意时间都会有一个task的stack等待被执行。执行一个task可能会触发更多的task被压入stack中。

Cascades优化器首先会拷贝原始的查询到初始化的search space中（在Cascades中，search space被称为“memo”，这是从Volcano继承来的）。然后通过一个任务对初始search space的top group进行优化，从而触发整个优化过程，进而会轮流触发search space中更小的子group的优化操作。优化一个group意味着找到这个group中的best plan（这杯称为一个“optimization goal”），因此会将rule应用于所有的expression。在这个处理过程中，新的task会被放置到task stack中，同时新的group和expression会加入到search space中。在完成对于top group的优化后，它会要求这个top group的所有subgroups各自完成优化，top group的best plan就可以被找到，这样就完成了优化。

和Volcano优化生成器一样，Cascades从top group开始执行优化过程，被认为是采用了一种top-down的搜索策略。动态规划和记忆化也在优化一个group的过程中被用到了。在初始化所有group的expression之前，它会检查是否同样的优化目标已经执行了；若是，那么它就简单返回在更早的search过程中找到的plan。Cascades和Volcano搜索策略中的一个主要区别在于Cascades只会在有需要的时候探索一个group，而Volcano则总是会在真正的优化阶段开始之前的第一个预优化阶段生成所有等价的logical expressions。在Cascades中，这两个阶段不是分离的。推导所有expression(如predicate)的所有逻辑等价形式是没有意义的。一个group只会在有需要的条件下使用transformation rule，并且它只会创建与给定pattern相匹配的group的所有成员。由于Cascades只会为真正有用的pattern探索group，它的搜索策略是更高效的。

与Volcano优化器生成器繁琐的用户界面相比，Cascades为DBI和优化器之间提供了一个简洁的数据结构抽象和接口。Cascades优化器和DBI之间的每个组成类都被设置为子类层次结构的顶层类。优化器只依赖于这个接口中定义的方法；DBI可以在定义子类时任意新增方法。一重要的接口会涉及到operator、cost模型和rules。这个清晰的接口非常重要，因为它让优化器更加健壮，并使DBI更容易实现或是扩展优化器。

Cascades只是一个优化器框架。它提出了多种性能改进，但许多特性目前未被使用或是仅以基本形式提供。Cascades当前的设计和实现还有许多优化的空间。优化器框架和DBI规范的强分离，虚方法的广泛使用，非常频繁的对象分配和回收可能会导致性能问题。一些剪枝技术可以应用在top-down的优化过程中，可以极大地提高搜索性能。所有这些发现都激发了我们对于Cascades的研究，并开发了一种新的、更高效的优化器-Columbia优化器。

Chapter 4. Structure of the Columbia Optimizer

基于Cascades框架，Columbia主要关注优化过程的效率。本章将会描述Columbia优化器的设计和实现细节。同时也会讨论其和Cascades的对比。

4.1 Columbia优化器概览

下图展示了Columbia优化器的接口。Columbia接受一个初始化的查询文本文件作为输入，使用DBI提供的同样是文本文件格式的catalog和cost model信息，并为这个查询生成最优计划作为输出。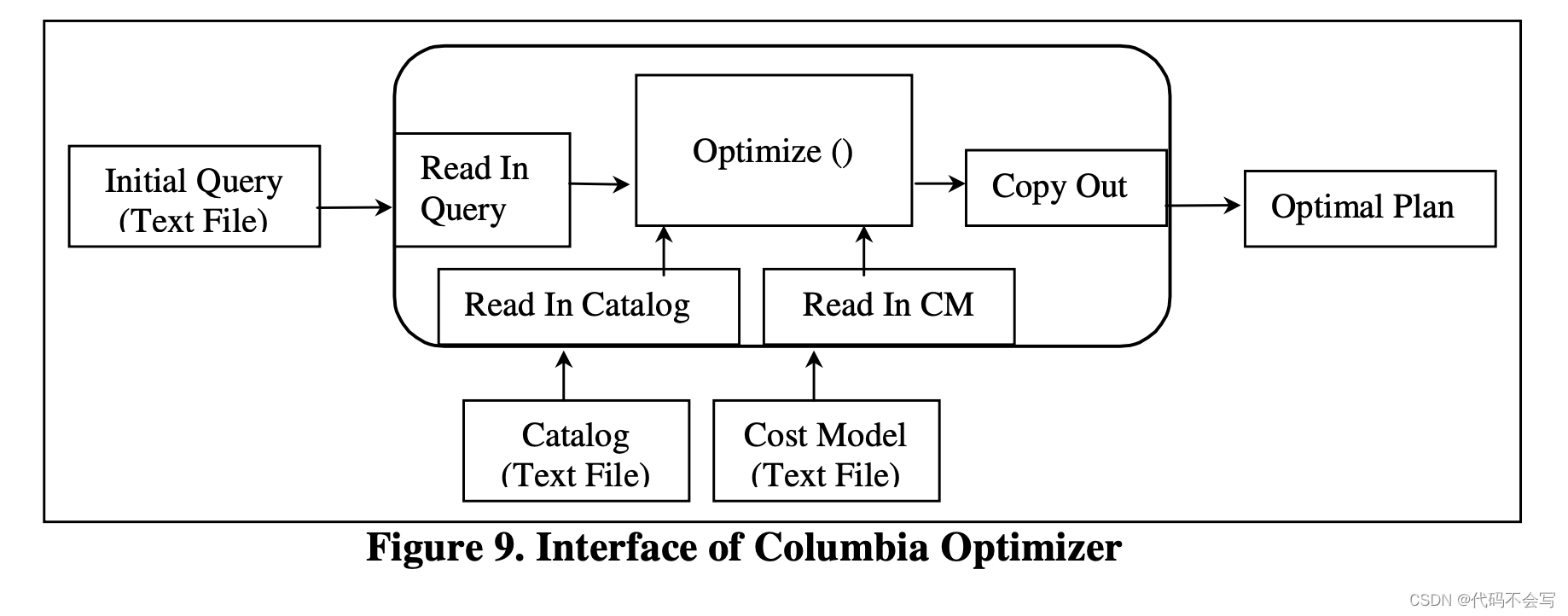

4.1.1. 优化器输入

在Columbia中，优化器输入是一个文本文件，其中包含以LISP样式树表示的初始查询树。一个tree由一个top operator和它的输入（如果有的话）组成，输入即是sub trees。每个tree或是sub tree都用括号分隔。

下表以文本格式展示了query tree的BNF定义。当前Columbia实现的logical operators包括GET, EQJOIN, PROJECT和SELECT，足以表达大多数的Select-Project-Join查询。这样的设计也可以支持logical operators的低成本扩展。（具体语法说明略）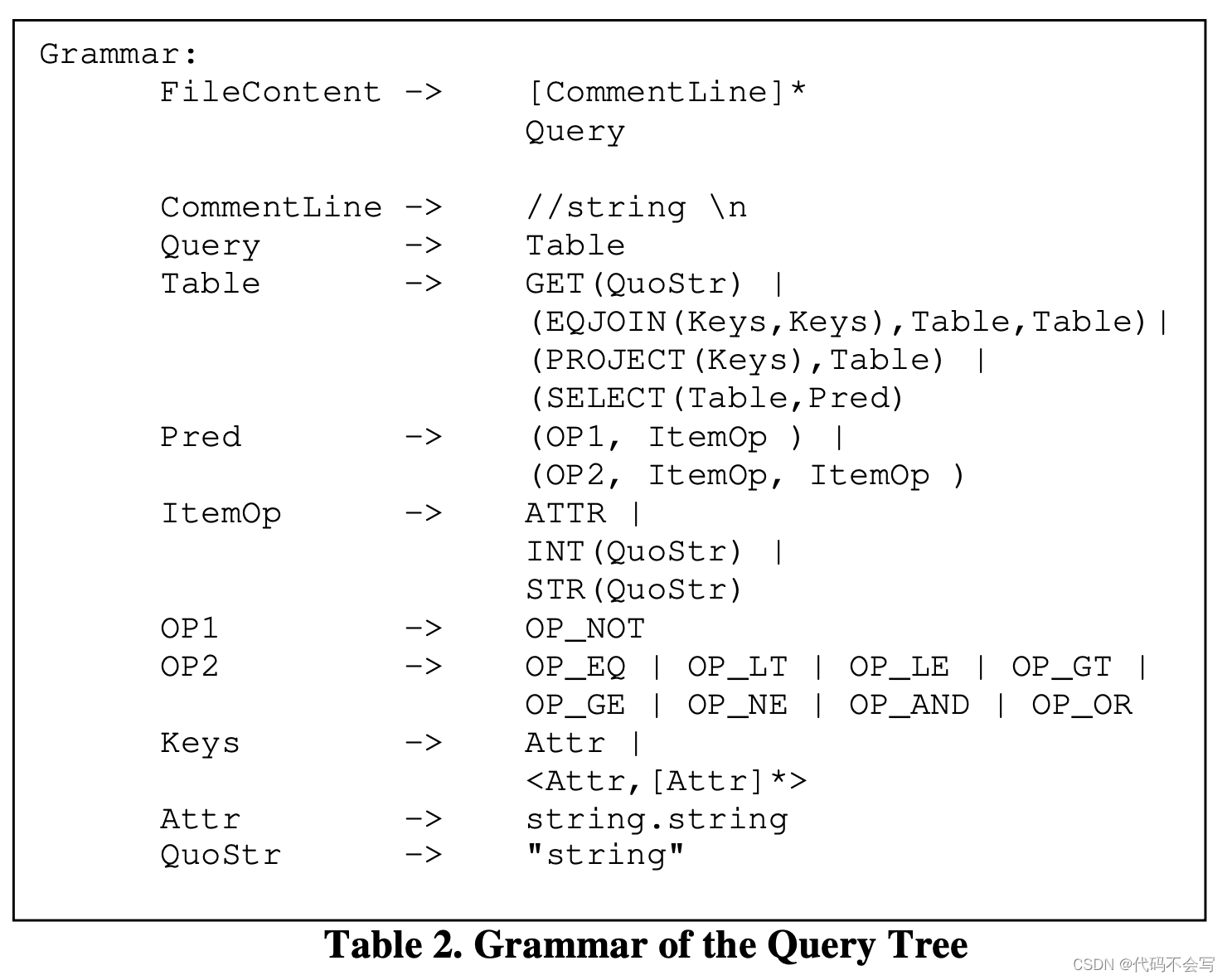

优化器中的Query Parser读取查询文本文件并将它以expression tree的形式存储。Expression tree是以一种递归的数据结构实现的，即类EXPR的一个对象，由一个Operator和0或多个EXPR对象的input组成。因此，query expression tree可以从root（top）expression开始遍历。Expression tree作为一个中间格式存在，在search space被初始化后它会被优化器拷贝到search space中去。这种模块分离允许高度的可扩展性。Query Parser和优化过程之间有一种松散的关联（它接收查询文本文件作为输入并输出一个query expression），因此parser中可以轻松地添加更多的操作来支持更多的功能，例如schema检查、查询重写等等。在Cascades中，初始化的查询以C++代码编写的expression tree标识，并内嵌到优化器的代码中。如果要优化另一个初始查询，则需要编译优化器的整个代码，以包括对初始query expression的更改。在Columbia中，只需要重写查询文本文件来表示新的初始查询，不需要编译代码。

下图展示了一个查询文本文件和对应query expression tree的样例。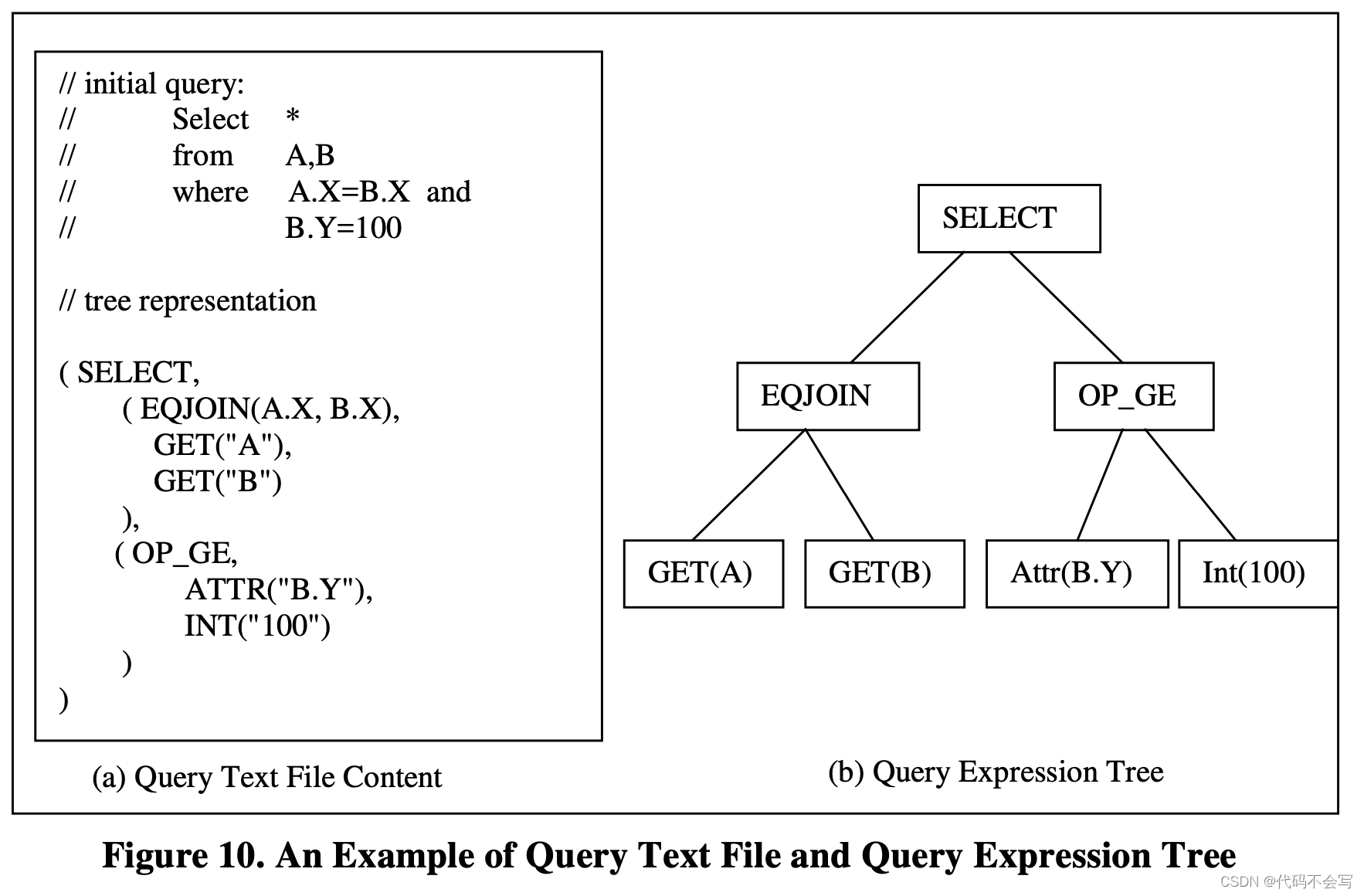

如上图，SELECT的predicate以expression tree的形式作为SELECT operator的input。在Columbia中，除了logical和physical operator，还有一个从Cascades继承来的item operator。Item operator和bulk operator（logical和physical operator）不同，它作用于一个固定数量（通常是一个）元组，而bulk operator作用于任意数量的元组。通常item operator可以认为是固定数量元组或是数值的函数。一个predicate代表了一个item operator的expression tree，返回一个bool值。Predicate的树形结构提供便捷的predicate操作，例如下推predicate through joins。

4.1.2 优化器输出

查询的最优计划是在优化处理过程中找到的，并被优化器复制出来。最优计划可以通过physical expression的缩进树形式打印出来，其代价和expression相关。最终的cost相对于特定的catalog和cost model来说是最优的。不同的catalog和cost model会对相同的查询输出不同的最优计划。

4.1.4 优化器的外部依赖

前面提到，优化器依赖于两种类型的信息：catalog和cost model。在Columbia中，catalog和cost model同样使用文本文件描述来提供扩展性和易用性。Catalog parser和cost model parser会读取这些信息，将它们存储到名为"Cat"和"Cm"的全局对象中。在优化处理过程中，优化器会从全局对象中获取信息并对应执行。、

当前Columbia支持简单版本的catalog和cost model，但文本文件的格式提供了后续的扩展性。

4.2 搜索引擎

下图展示了Columbia search engine的3个重要组件及它们之间的关系。Search engine是通过拷贝初始的query expression来初始化的。优化器的目标是扩展search space并在最终的search space中找到最优执行计划。在Columbia中，优化过程是通过一系列的“tasks”控制的。这些task会对search space中的group和expression进行优化，应用rule set中的rule，通过生成新的expression和group来扩展search space。在优化完成后，最终search space中的最优执行计划会作为优化器的输出被拷贝出来。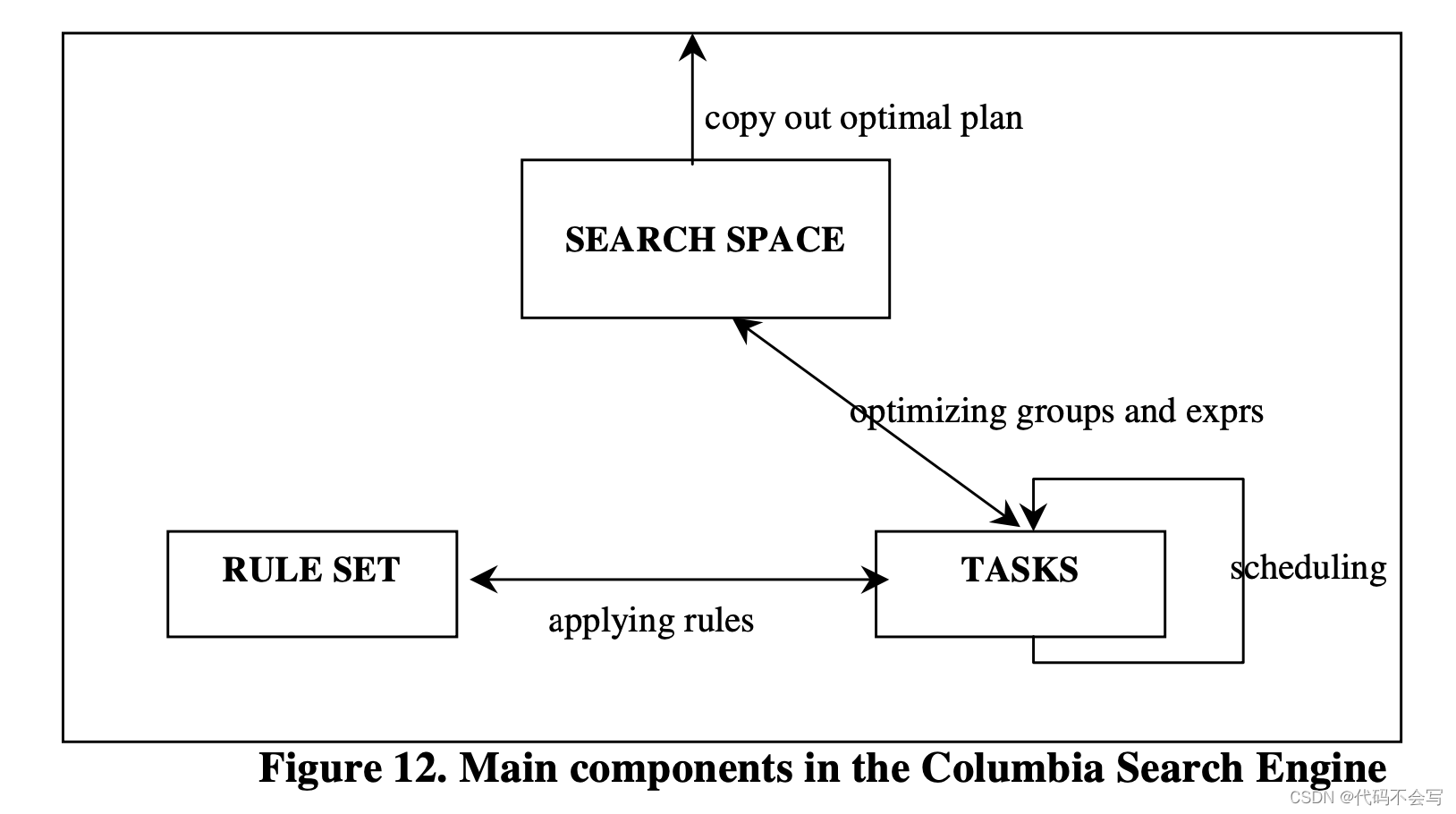

4.2.1 搜索空间

Search space中的组件是groups。每个group包含一个或多个逻辑等价的expression。

4.2.1.1 搜索空间结构 - SSP类

Search space概念是从AI中借鉴来的，它是一种解决问题的工具。在查询优化中，问题是基于特定的上下文为一个给定的查询找到最优计划。一个search space通常由一系列可能的问题及其子问题的解决方案组成。动态规划和记忆化是两种使用search space来解决问题的方案。它们都是通过逻辑等价来划分可能的解决方案。我们称每一个分区为一个Group。因此，search space有一系列的groups组成。

在Columbia中，一个和Cascades中MEMO数据结构类似的数据结构用来代表search space，我们称之为一个SSP类的实例，它包含一个group的数组，带有一个group ID来标识search space中的root group。Search space中的一个group包含一个逻辑等价的multi-expression的集合。如前面介绍，一个multi expression由一个operator及0或多个group作为input组成。因此，search space中的每个group要么是root group，或是其他group的input group。所有其他的group都可以作为root group的后代被访问到。这也是root group必须被标识出来的原因。通过拷贝初始的query expression，search space可以使用几个basic group进行初始化。每个basic group只包含1个logical multi-expression。优化过程中进一步操作会通过增加新的multi-expression和新的group到search space中来扩展search space。“CopyIn”方法会将一个expression复制为一个multi-expression并将这个multi-expression放置到search space中。它可能会将这个新的multi-expression放置到一个与其逻辑等价已有的group中，或是将这个新的multi-expression放置到一个新的group中，此时该方法会新建group并附加到search space中。SSP类中的“CopyOut”方法会在优化结束后输出最优执行计划。

4.2.1.2 搜索空间中的重复Multi-Expression检测

将一个multi-expression放置到search space中的潜在问题是可能会发生重复，即，search space中可能会有一个和次multi-expression完全一样的multi-expression。因此，在实际的添加操作前，这个multi-expression的重复行必须先在search space中进行检查。如果存在重复，那么就不应该添加。

为了检查重复性，至少有3个算法可用：

某种基于树的搜索
可扩展的hash
静态hash

尽管算法1和算法2当前已有一些代码实现，但它们比较复杂，并且很难说在这种场景下是否有效。备选方案3很简单，易于实现，尽管当multi-expression的数量出现指数增长时会出现问题。一个适用于小查询的，有固定数bucket的hash table在优化大查询时可能每个bucket都被多个元素填满，因为会生成更多的expression。

Cascades和Columbia都是用了静态hash（备选方案3）来支持multi-expression的快速重复检测。因此固定bucket数量的潜在问题是不可避免的。Search space中包含一个static hash table。multi-expression的所有三个组成部分，即operator class name、operator parameters和input group numbers，都被散列到hash table中以检查重复。Columbia和Cascades中的主要区别是Columbia使用了一个高效的hash函数。

和Cascades中使用传统hash函数（随机并质数取模）不一样，Columbia选择了一个高效的hash函数“lookup2”，这是一个由Bob Jenkins写的原始哈希函数LOOKUP2的修改。Jenkins声称LOOKUP2和许多传统hash函数相比更简单且高效。hash后key中的每一个bit都使用简单且快速的操作和其他3个“magic”数值进行混合，例如加法、除法和位操作。key中的每一个bit都会影响返回value中的每一个bit。lookup2的另一个优势在于它的hash table的大小是2的幂，这可以允许非常快的模操作。相反，一个传统的hash函数要求对素数进行模运算，这比对于2的幂的模运算要慢得多。考虑到hash操作的大量性，hash函数的效率是非常重要的。

由于重复仅仅会在优化期间（physical expression是基于logical expression唯一生成的）针对logical multi-expressions发生，优化器生成的所有logical multi-expressions都要进行hash，以便在加入search space时检查重复性。一个multi-expression有3个组成部分：一个operator class name，operator 参数和零或多个input group。为了最大化hash值的分散性，Columbia使用了这三个组成部分作为一个multi-expression的key。这三个部分依次应用于哈希函数:首先将operator class name哈希为一个值，该值作为hash operator argument的初始值。然后，这个散列值又被用作对input group进行散列的初始值。最后的散列值作为multi-expression的散列值。

SSP类的“FindDup()”方法实现了重复检测。Search space中的hash table中包含了指向search space中logical multi-expression的指针。FindDup方法接收一个multi-expression作为参数并返回在search space中的重复multi-expression（如果发现重复的话）。FindDup的算法是这样的：首先，multi-expression的hash value会被计算，然后hash table会遍历查找是否有冲突，如果有，那么会按照简单性的顺序比较两个multi-expression，例如，首先比较operator的数量，然后input groups，最后比较operator arguments。如果没有发现重复，那么新的multi-expression会被链接在原始multi-expression后面，使用相同的hash value。如果hash table没有发现冲突，那么新的multi-expression就会被直接加入到hash table中。

考虑到search space中的multi-expression数量非常多，Columbia的这种哈希机制可以在整个search space中简单有效地消除multi-expression的重复。

4.2.1.3 Group

Group类是top-down优化中的核心。一个group包含一个逻辑等价的logical和physical multi-expression的集合。由于所有的multi-expression都有相同的logical properties，Group类也会存储一个由所有multi-expression共享的logical property的指针。为了实现动态规划和记忆化，引入了一个记录着group中最优plan的winner结构。除了这些group的基本元素之外，Columbia还改进了这个类以支持更有效的搜索策略。与Cascades相比，改改进措施包括：增加了下界成员lower bound member，分离了physical和logical multi-expression，以及更优的winner结构。

Group中的Lower Bound：group中的lower bound是一个值L，group中的每一个plan P必须满足：cost(P) >= L。Lower bound是top-down优化策略中的一个重要指标，当一个group的lower bound大于当前的upper bound时，就可能会发生group剪枝。Group剪枝可以避免全量input group的枚举，同时不会错过最优plan。在4.4.1章节中我们会讨论Columbia中group剪枝的细节，这对于Columbia优化器的效率产生了重要的贡献。Group中的lower group在group被创建时就会计算，并存储在group中，以在后续的优化操作中使用。

本章讨论如何在Columbia中获得group的lower bound。显然，lower bound越高越好。我们的目标是在从group中收集到的信息中找到最高的可能lower bound。当一个group被创建时，logical property会被收集，包括cardinality和group的schema，lower bound就是从它们中派生出来的。由于lower bound只依赖于group的logical property，它可以不需要枚举group中的任一expression就能被计算出来。

在描述lower bound的计算之前，我们先给出一些定义：

touchcopy()：是一个返回数字值的函数，对于任何join，该值都小于join的cost除以join输出的cardinality。这个函数代表生成输出元组所需的访问两个所需要的元组的cost，以及将结果复制出来的cost。
Fetch()：是从disk获取一个byte的平摊成本，假设所有的数据都是以block的形式访问的。
|G|：代表group G的cardinality
给定一个group G，如果一个基础table A的一些属性X满足A.X在G的schema中，我们称这个基础table在G的schema中。则cucard(A.X)标识列A.X在G中的唯一cardinality，G中的cucard(A)代表在所有G的schema中所有A.X属性中cucard(A.X)的最大值。在不失一般性的前提下，我们假定G schema中的基表是A1，…， An, n >= 1, 同时 cucard(A1) <=…<= cucard(An)。

一个group中的lower bound计算方式如下图：

上图中，我们为group定义了三种类型的lower bound。这三种lower bound是互相独立的，因此它们汇总起来就为一个group提供了lower bound。

对于G中的top join的touch-copy。它基于G的cardinality，因为G中任意一个plan输出的元组集合就是group中的top join的输出。通过定义touchcopy()，任意join（包括copy-out cost）的cost至少是touchcopy()乘以最终join的cardinality。
对于G中non-top join的touch-copy bound。它基于G中列的唯一cardinality，例如，G schema的attributes的结构。我们能证明这个touch-copy bound是non-top joins的lower bound。（证明过程略）
对于G中的叶子节点（base tables）的fetch bound。它同样基于G schema的attributes的结构，对应从base table获取元组的cost。（证明过程略）

logical和physical multi-expressions的分离。Cascades将logical和physical multi-expressions存储到一个独立的linked list。Columbia中将它们存储在独立的list中，这从两方面节省了时间。

首先，rule会将所有的logical multi-expressions作为input来检查它们的pattern是否匹配，因此我们不需要遍历physical multi-expressions。一个group通常会包含大量的logical和physical multi-expressions，这些expression可能会占据好几个page的virtual memory，因此一个对于physical multi-expressions的独立引用可能会导致memory page错误，这可能会极大地降低程序执行的速度。通常，一个group中physical multi-expressions的数量是logical multi-expressions的两倍或三倍。通过分离logical和physical expression并只查看logical expression，Columbia中的rule绑定应该比Cascades更快。

其次，如果已经对一个group进行了优化，并正在针对另外一个property进行优化，我们可以将group中的physical和logical multi-expressions进行分别处理。Physical list中的physical multi-expressions被扫描，仅仅是为了检查是否符合要求的property一级直接计算cost，logical list中的logical multi-expression被扫描仅仅是为了看是否所有适当的rule都被执行的。只有当一个rule之前没有应用到一个expression时，logical expression才会被优化。在Cascades中，优化一个group的task不会关注physical multi-expressions，而是所有的logical multi-expression都需要被再次优化。显然，Columbia中对于group的优化方法优于Cascades，并且在group中分离logical和physical linked list有助于优化group。

更优的winner结构。动态规划和记忆化的关键思想是将搜索的winner存储起来供后续使用。每个问题或是子问题的最优解决方案的搜索都是基于上下文执行的。一个上下文由required physical property(eg. 数据必须按照A.X排序)和一个upper bound(eg. 解决方案的cost必须小于5)组成。一个WINNER是一个physical multi-expression，它在上下文的搜索中获胜并能指导search。由于不同的search上下文可能对于一个group产生不同的winner，因此group结构中会存储一个winner对象的list。

在Cascades中，一个Winner类包含一个指导search的context，和一个在search中获胜的multi-expression的pair组成。

在Columbia中，对Winner数据结构进行了简化。Columbia中的Winner不需要存储context以及连接到其他winner的链接，一个Winner类由一个在search中获胜的multi-expression、该expression的cost和search所需的required physical property组成。一个group中的winner对象代表着这个group的可能搜索结果。因此一个group会有一个winner数组，没有必要存储group中下一个winner的指针。很显然Columbia中的winner结构比Cascades中的更简单、更小。在Columbia中，winner也是用于存储搜索的临时结果。在group中的physical multi-expressions的cost被计算时，迄今计算的成本最低的一个expression会被存储为一个winner。在优化过程中，winner会被不断更新，并最终找到最佳的plan。有些时候，当根据required physical property无法找到physical multi-expression时，我们会将winner中的multi-expression指针存储为NULL，以表明当前这个physical property没有inner。由于winner同样是子问题搜索的解决方案，这个信息会被记忆下来并在后续的优化过程中被使用到。下面是Columbia中的Winner类结构：

4.2.1.4 Expressions

Expression对象有两种分类：EXPR和M_EXPR。EXPR对象对应于查询优化中的一个expression，它代表着优化器中的一个查询或是子查询。EXPR对象是一个带有参数的operator（OP类），加上一个指向input expressions的指针（EXPR类）。为了方便，它保留了operator的参数数量。EXPR被用来代表初始和最终的查询，并在rule的定义和绑定中使用。

M_EXPR实现了multi-expression接口。它是一个利用了共享的EXPR的紧凑形式。M_EXPR是一个带有参数的operator加上一个指向input GROUP而不是EXPR的指针，因此一个M_EXPR包含了几个EXPR。M_EXPR是group中的主要组件，并且所有的搜索都是基于M_EXPR完成的。因此必须有一些和M_EXPR相关的状态。下表展示了类M_EXPR的数据成员及Cascades中实现了multi-expression的对应类EXPR_LIST。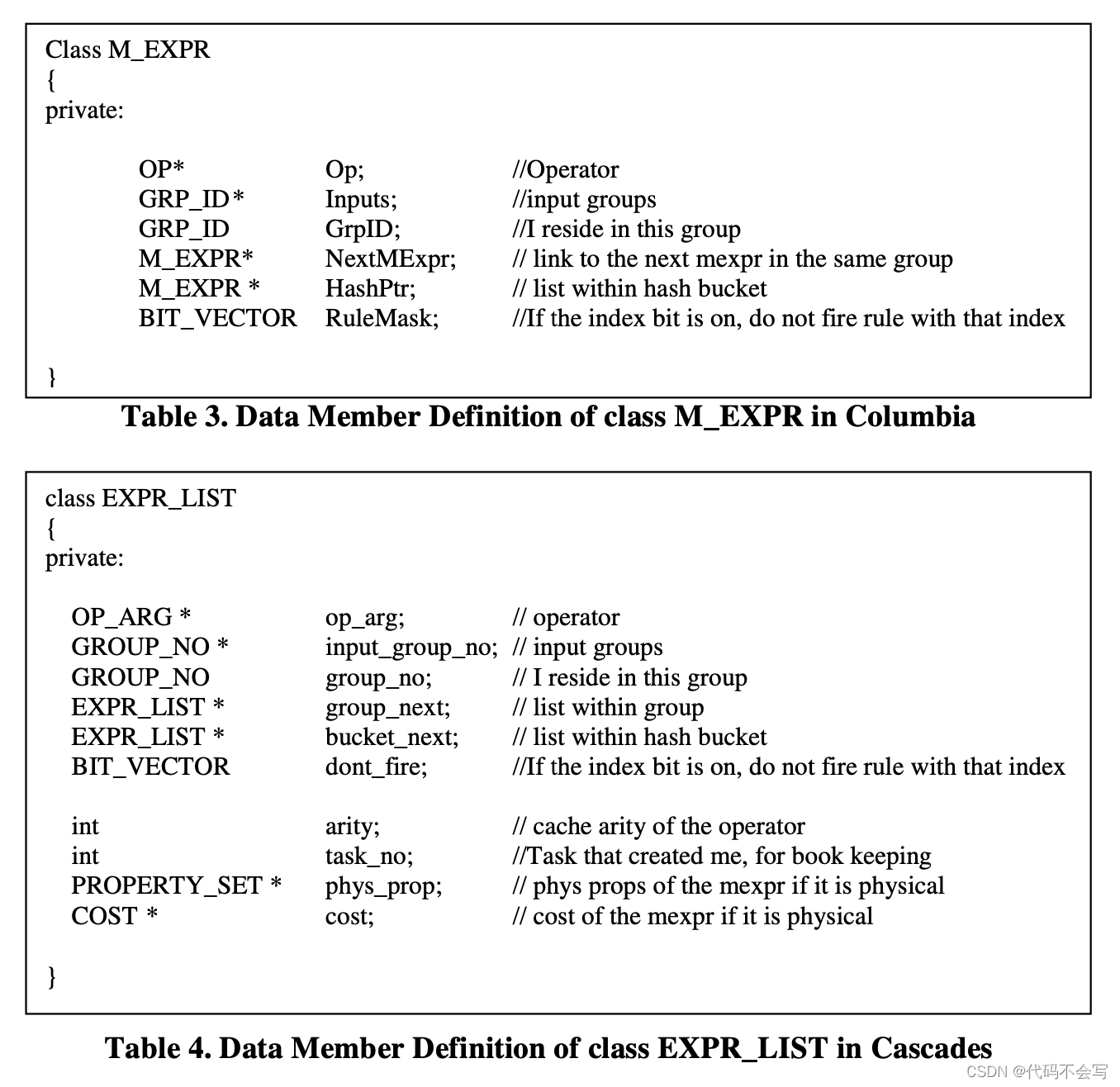

上图展示了Columbia和Cascades针对multi-expression的两个实现类。我们可以发现，Columbia中的M_EXPR数据成员更少。EXPR_LIST中的额外数据成员在M_EXPR中根本不需要：M_EXPR的参数数量可以从operator获得。没有必要跟踪创建M_EXPR的任务，也不需要存储physical M_EXPR的physical properties和cost，因为它们一旦被计算并作出决定，在任何地方就不会再使用了。由于multi-expression占据了search space中的主要内存，使这个数据结构尽可能简洁是非常关键的。例如，一个M_EXPR对象占用24 bytes内存，而EXPR_LIST对象占用40bytes内存。EXPR_LIST和M_EXPR的内存使用比例大概是1.67 : 1。如果初始查询是一个10个table的join，那么根据前面的数量级推断至少会有57k个logical multi-expressions。在Columbia中这些logical multi-expression会占用24*57k = 1368k bytes 内存，在Cascades中会占用40*57k = 2280k bytes内存。因此，Columbia中简洁的数据结构大大地节省了内存用量。

4.2.2 Rules

优化中搜索过程的rule是在一个rule set中定义的，它独立于search structure和算法。Rule set可以通过增加或是删除rule进行独立修改。附录C中展示了用于优化简单join查询的一个简单的rule set。

所有的rule都是RULE类的实例，这个类提供了rule name、一个先行词（即pattern）、和一个结果（substitute）。Pattern和Subsitute都是用expression（EXPR对象）来表示的，它们都包含leaf operator。一个leaft operator是一个特殊的只在rules中使用的operator。它没有input并且是一个pattern或是substitute expression tree中的leaf。在匹配rule时，pattern中的leaf节点可以匹配任意的子树。例如，Left To Right (LTOR) join连接rule有以下成员数据，其中L(i)代表Leaf operator i:

Pattern: ( L(1) join L(2) ) join L(3)

Substitute: L(1) join ( L(2) join L(3) )

Pattern和Substitute描述了如何在search space中产生新的multi-expression。新的multi-expression是通过APPLY_RULE::perform()方法产生的，分为两部分：首先，一个Bindery对象会生成Pattern到search space中EXPR的绑定；然后RULE::next_substitute()会产生新的expression，通过SSP::copy_in()方法集成到search space中。

Rule类中还有其他方法来协助rule的执行。top_match()方法会检查rule的top operator是否和当前希望应用rule的expression的top operator匹配。这个top match会在实际rule绑定之前执行，因此消除大量显然不匹配的expressions。

promise()方法从来决定rule应用的顺序，甚至直接不应用rule。promise()方法返回一个rule对与优化上下文（例如，我们需要考虑的required physical properties）的promise value。因此它是一个运行时的value，炳辉通知优化器该rule可能有多有用。小于等于0的promise value意味着不会调度这个rule。越高的promise value意味着会越早调度该rule。默认情况下，一个implementation rule会有值为2的promise，其他rule的promise为1，意味着implementation rule总是会被更早调度。Rule的调度机制允许优化器来控制搜索顺序，并通过调度rule来尽可能早、尽可能低成本地获得尽可能搜索边界。

Columbia继承了Cascades中关于rule机制的基础设置，但是做出了几个优化，包括绑定算法和对enforcer的处理。接下来的章节会介绍这些优化的细节。

4.2.2.1 Rule Binding

所有基于rule的优化器都必须在search space中将pattern绑定到expression上。例如，对于LTOR join相关rule，包含2个成员数据。L(i)代表下标为i的LEAF_OP：

Pattern: ( L(1) join L(2) ) join L(3)

Substitute: L(1) join ( L(2) join L(3) )

每一次优化器应用这个rule，它都必须将这个pattern绑定到search space中的一个expression上。一个简单的绑定如下：

( G7 join G4 ) join G10

其中Gi是带有GROUP_NO i的group。

一个BINDERY对象执行识别对给定pattern的所有绑定的重要任务。BINDERY对象会在它的生命周期中生产所有的绑定。为了生产一个绑定，一个bindery必须为每一个input subgroup生成一个bindery。例如，一个LOTR 相关rule的bindery，会为left input生成一个bindery，它会寻找所有对于L(1) join L(2)的pattern的绑定，以及它会为right input生成一个bindery，它会找到所有对于L(3) pattern的绑定。最终right bindery只会找到一个绑定，即整个right input group，而left bindery通常会找到多个绑定，left input group中每个join对应一个绑定。

Bindery对象分为两种类型：expression bindery和group bindery。Expression bindery将pattern到一个group中唯一的一个multi-expression上。Expression被一个作用于top group的rule使用，来绑定一个expression。Group bindery，为input group的使用而生成，会绑定一个group中的所有multi-expression。由于Columbia和它的前身只会将rule作用于logical multi-expressions，bindery对应也只会绑定logical operator。

由于search space中有大量的multi-expression，rule binding是一个耗时的任务。实际上，在Cascades中，寻找binding的Bindery::advance()函数是整个优化器系统中代价最高的函数。任何对于rule binding算法的提升都一定会导致优化器的性能提高。Columbia重定义了Bindery类和绑定算法来让rule binding过程更高效。

由于一个bindery可能会绑定search space中的多个Expr，它会经历几个stage，通常是：start，然后循环几个有效binding，最后结束。在Columbia中，这些stage由3个binding states标识，每一个都是枚举类型BINDERY_STATE中的一个。定义如下：

在Cascades中，binding算法会使用更多的states来跟踪所有的binding stages，因此使得算法更复杂并消耗了更多的CPU。在Cascades中，binding stages通过6个binding states来表示。Columbia定义如下：

在Columbia中，binding算法是在BINDERY::advance()方法中实现的，它被APPLY_RULE::perform()调用。binding函数会遍历许多嵌入在search space中的tree，已找到可能的bindings。遍历是用有限状态机完成的。如下图。

4.2.2.2 Enforcer Rule

Enforcer rule是一个特殊类型的rule，它会插入physical operators来强制或保证所需的physical properties。被enforcer rule插入的physical operator被称为enforcer。通常来说，一个enforcer会以一个group作为input并输出同一个但具有不同physical property的group。例如，QSORT physical operator是一个enforcer，它在一个搜索空间中由group标识的元组集合上实现了QSORT算法。SORT_RULE是一个enforcer rule，它将QSORT operator插入到了substitute中。这个rule可以按如下的方式表示：

Pattern: L(1)

Substitue: QSORT L(1)

L(1)代表下标为i的LEAF_OP

当search context要求一个有序的physical property是，一个enforcer rule就会被触发。例如，当一个merge-join被优化时，它的input的search context会有一个required physical propert来要求input是按照merge-join的attributes有序的。例如下面的multi-expression

MERGE_JOIN(A.X, B.X), G1, G2

当使用top-down方法来优化这个multi-expression时，input首先要在特定的context中优化。对于left input group G1，search context中的required physical property会要求按照A.X有序，同时right input group G2会有一个按照B.X有序的required physical property。当search要求一个有序的property时，SORT_RULE会被触发来插入QSORT opeartor以强制input group具有required property。

另外一个enforcer rule也是相似的，例如，HASH_RULE，会强制产生一个hashed physical property。Enforcer rule是否会被触发，取决于rule对象中的promise()方法。promise()方法只有当search context具有required property例如sortes或是hashed，时才会返回一个正的promise值。如果没有required physical property，那么会得到一个值为0的promise，意味着enforcer不会被触发。

Cascades和Columbia处理enforcer rule时有2个主要的差异：

首先，excluded property。Cascades使用promise()方法中的excluded properties（？？）来决定一个enforcer的promise值。只有当required physical property set和exclude physical property set同时不为空时，promise()方法才会返回一个非0的promise值。使用excluded property的目的是为了避免对一个group重复使用相同的enforcer。但是这些excluded properties很难跟踪并且会使用更多内存（它要求search context包含一个指向excluded property的指针），并且会使search算法处理enforcer更复杂。而Columbia不会使用excluded properties。Columbia中的context只包含一个required property和upper bound。promise()方法只根据required physical property来决定一个rule的promise值。为了避免重复应用enforcer rule的潜在问题，会对enforcer rule使用unique rule set技术。即，每个M_EXPR都有一个RuleMask数据成员，包含每一个enforcer rule的bit。当一个enforcer rule被触发，这个rule对应的bit位会被设置为on，意味着这个enforcer rule已经对这个multi-expression使用了。在下一次触发enforcer之前，会检查rule mask，不会再重复触发rule。另一方面，这个简单的方法导致了一个潜在的问题：如果一个group已经被优化了，而我们需要针对另外一个不同的property来执行优化，此时multi-expression中的enforcer rule bit可能由于上一次的优化已经被设置为on了。那么在这个新的优化阶段中，这个enforcer rule则不会针对不同的property再被执行，即便它对于这个新的physical property有一个非常好的promise值。因此，优化器可能会在这个优化阶段给出错误的答案。这个问题的解决方案导致了Columbia基于Cascades的另外一个改进。见下面第二个差异点。

其次，representation of enforcers。在Cascades中，enforcer由一个带参数的physical operator表示。例如，一个QSORT operator有两个参数：一个是需要排序的attributes，另一个是排序顺序（asc or desc）。QSORT::input_reqd_prop()方法返回required physical property，并未input返回一个经过排序的excluded property。它在向下优化一个multi-expression时为input提供了search context。Enforcer实际上是由enforcer rule生成的。在一个enforcer rule成功绑定到一个expression上之后，RULE::next_substitute()方法被触发以生产一个新的expression，其中插入了enforcer。enforcer的参数是根据search context中的required physical properties产生的。例如，如果search context有一个required physical property要求按照attributes <A.X, A.Y>有序，那么enforcer会生成一个带有参数<A.X, A.Y>的QSORT，表示为QSORT(<A.X, A.Y>)。这个新的带有enforcer的expression会加入与之前expression到相同的search space中的group中。由于enforcer有参数，具有相同name但是不同参数的enforcer会被认为是不同的enforcers。我们可以从这里看到，如果search带有许多不同的required physical properties，例如基于不同的attributes的排序，那么就会有许多有相同name但是不同参数的enforcers在search space的group。这可能是一个潜在的浪费。

相反，在Columbia中，enforcer由一个不带参数的physical operator表示。例如，一个QSORT enforcer标识为QSORT()，不包含任何参数。在优化过程中，只会在group中产生一个QSORT operator，因为在第一次SORT_RULE执行后，expression中对应的rule bit被置位并组织了后续的SORT_RULE应用。这个方法是安全的，因为我们会假设对于一个input stream的sort操作会产生相同的cost，忽略了sort keys。以下是Columbia优化器的工作原理：如果一个group已经针对一个property被优化过了，那么一个enforcer multi-expression就会被加入到group中。现在我们再针对另外一个property进行优化，那么相同的enforcer就不会再被重复生成了，因为对应的rule bit已经被置位了。因此enforcer rule就不会再被执行。另一方面，group中（包括enforcer multi-expression）所有的physical multi-expression会被检查确认期望的property是否得到满足，并在新的context中使用新的required physical property直接计算cost。由于enforcer没有参数，它会满足新的physical property，然后这个enforcer multi-expression的cost会基于新的physical property被计算，它和这个physical property会被存储在winner结构中，和普通的multi-expression winner一样。

当优化器准备将最优plan拷贝出来时，enforcer winner需要一个特殊的处理，即针对required physical properties为它们添加参数，因为实际的enforcer implementation需要参数。例如，假设enforcer multi-expression“QSORT(), G1”是一个针对physical property“sorted on A.X”的winner，当我们从这个winner进行拷贝时，实际的plan是“QSORT(A.X), G1”，即它会将真实的参数添加到enforcer中。

4.2.3 Tasks-Search Algorithm

Task是搜索过程中的一个活动。原始的task是对整个query的优化。Task之间可以互相创建和调度，当没有还未完成的task时，就意味着优化结束了。每个taks都和一个特定的context关联，并有一个“perform()”方法来真正执行task。Task类是一个抽象类，特定的task会继承它并实现一个虚方法“perform()”。PTasks类包含一组未完成需要调度和执行的tasks。PTask当前一stack结构实现，具有一个“pop()”方法来将一个task移除以执行，以及一个“push()”方法来讲一个task存储到这个stack结构中。一个PTasks对象是在优化之处创建的，此时优化top group的原始task会被push到PTasks中。当优化开始时，原始task会被pop out并调度其perform()方法以触发实际优化的开始。优化过程中会创建其余的task，push到PTasks中进行后续的调度。下图展示了优化主过程的伪代码。通过使用抽象类，我们可以实现简单清晰的代码结构。

整个搜索算法是通过优化器中所有指定task的执行完成的。Columbia中的tasks包含：group optimization（O_GROUP）、group exploration（E_GROUP）、expression optimization（O_EXPR），input optimization（O_INPUTS）、rule application（APPLY_RULE）。下图展示了tasks之间的关系。箭头表明了哪一类的task会调度（触发）另一类。本章接下来的内容会描述Columbia中每一个task的实现细节。在每个task的描述中，同样会加上和Cascades的比较。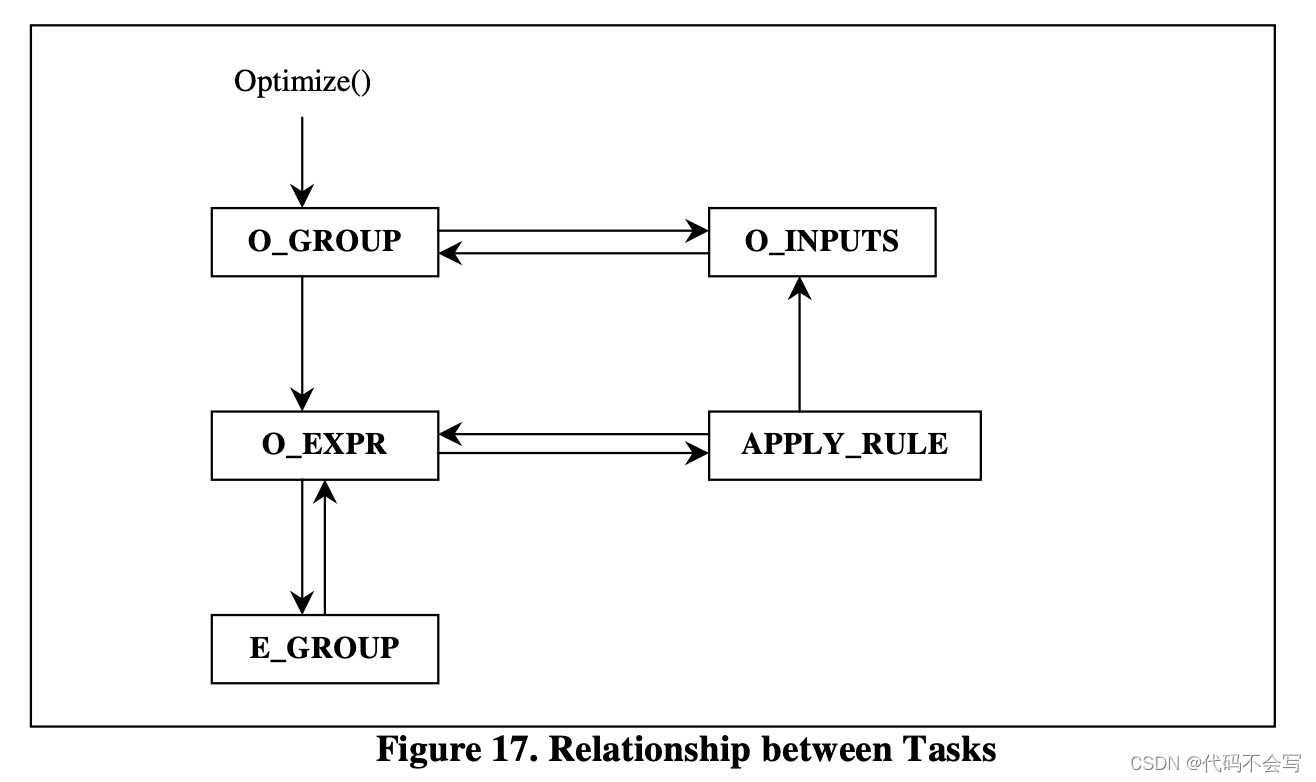

4.2.3.1 O_GROUP - Task to Optimize a Group

这个task会基于一个给定的context找到group中代价最低的plan，并将它（和context一起）存储到这个group的winner数据结构中。如果没有最优的plan（例如，upper bound限制不满足），这个context会带着一个为null的plan存储到winner结构中。这个task会为group生成所有相关的logical和physical expression，计算所有physical expression的cost并选择代价最低的那个。O_GROUP task会创建另外2种类的task来对group中的expressions进行生成和优化：O_EXPR、O_INPUTS。

动态规划和记忆化都会再task中使用到。在初始化一个group中所有expression的优化之前，它会检查是否已经有同样的优化目标已经被执行了（即相同的search context）；如果是，那么它会简单返回之前搜索所找到的plan。重用已导出的plan是动态规划和记忆化中至关重要的方面。

下图展示了O_GROUP task中的处理过程，它通过O_GROUP::perform()方法实现。

如上图，group中logical和physical multi-expression的分离方便了此任务中的搜索。

执行O_GROUP task时有两种case：

第一种，第一次优化一个group（eg. 对于一个context搜索一个group）：在这种场景下，group中只会有一个logical mexpr（初始expr）。根据算法，只会有一个task，即针对初始mexpr的O_EXPR，会被创建并push到task stack中，它会通过apply rule来生成另外一个expression。

第二种，在一个不同的context下优化一个group时，例如，一个不同的required physical property：在这种场景下，group已经被优化了并且可能有几个winners。因此group中可能会有多余一个的logical和physical multi-expression。我们需要做两件事：1. 我们需要带着新的context在每一个logical multi-expression上执行O_EXPR。因为在新的context下，一些不能应用于某个mexpr的rule会变得适用。由于唯一rule set技术，我们不会触发同样的rule两次，这避免了在group中生成重复的multi-expressions。2. 我们需要在新的context下对每一个physical mepxr执行O_INPUTS来计算这个physical mexpr的cost，并在可能的情况下为这个context生成一个winner。

在Cascades中，优化一个group的task不会处理physical multi-expressions。对于一个group的所有logical multi-expression，task会针对每一个logical multi-expression创建O_EXPR task并push到stack中。然后所有的physical multi-expression会被生成并计算cost。在第二次优化group时，会再次基于一个不同的context生成所有的physical multi-expression并计算cost。由于所有的logical和physical multi-expression存储在一个linked list中，这个方法必须遍历一个group中的所有physical multi-expressions。基于这一点比较，Columbia中优化group的算法比Cascades更高效。

4.2.3.2 E_GROUP - Task to Expand the Group

一些rule要求它们的inputs包含特定的目标opeartor，通常是logical operators。例如，一个join结合律rule要求其中一个input必须是join。当一个multi-expressions中的join operator和rule中的top join operator匹配时，这个multi-expression的left input group必须被扩展来查看group中是否有join，因为rule要求left input必须是一个join。并且group中所有的join都必须match rule中的left join。

一个E_GROUP task通过创建所有应该属于该group的目标logical operators来扩展一个group，例如，触发可以创建归属于一个join group的所有join的任何规则。这个task只会在根据rule的pattern需要进行exploration时按需调用。它由O_EXPR task按需创建并调度。

下图展示了explore一个group的过程。它被E_GROUP::perform()方法实现。

动态规划同样用于避免重复工作。在explore一个group的expressions之前，task会检查当前group是否已经被explore过了。若是，task会在不产生其他task的前提下立刻终止。当需要exploration时，task会为每个logical multi-expression触发一个O_EXPR task，并为这个multi-expression携带“exploring” flag以通知O_EXPR task来explore expression，即，仅对expressions执行transformation rule。

在Cascades中，一个E_GROUP task会创建其他类型的task，E_EXPR，来explore一个multi-expression。由于E_EXPR和O_EXPR有同样的行为，Columbia没有E_EXPR task。Columbia只是通过带有flag复用O_EXPR的方式表明task的目的。

4.2.3.3 O_EXPR - Task to Optimize a Multi-Expression

Columbia中的O_EXPR task有两个目的：一是优化一个multi-expression。这个task会触发multi-expression的rule set中的所有rule，按照promise排序。在这个task中，transformation rules会被触发来expand expression，生成新的logical multi-expressions；同时implementation rules会被触发以生成对应的physical multi-expressions。O_EXPR的另一个目的是explore一个multi-expression来为rule match做准备。在这个场景下，只有transformation rules会被触发，同时只有新的logical multi-expression会被生成。O_EXPR task有一个flag，来说明task的目的。默认情况下，这个flag被设置为“optimizing”，因为O_EXPR task还是更多地用于优化一个expression。如果tas是被用于explore，特别是由E_GROUP task衍生的情况下，这个flag会被设置为“exploring”。

下图展示了O_EXPR task的算法，有O_EXPR::perform()方法实现。在O_EXPR::perform()中，优化器会决定那个rule需要被push到PTASK stack中。注意，rule的promise是在top-most operator的input被扩展和与rule的pattern匹配之前评估的，而promise值被用于决定是否expand这些input。

Columbia和Cascades关于优化一个multi-expression的算法没有主要的区别，除了Columbia复用了O_EXPR来explore一个multi-expression。在Cascades中，使用了一个新的task，即E_EXPR来exploring。

4.2.3.4 APPLY_RULE - Task to Apply a Rule to a Multi-Expression

Columbia和Cascades中apply rule的算法没有差异。一个rule只会应用到logical expressions上。APPLY_RULE是将一个rule作用于一个logical multi-expression并生成新的logical或是physical multi-expressions到search space中的task。给定一个rule和一个logical multi-expression，task会决定所有当前seach space中可用expressions的所有合理pattern bindings，然后应用该rule并在search space中添加新的substitue expressions。新生成的multi-expressions如果是logical multi-expressions，那么就会在接下来的transformation中被优化，如果是physical multi-expression则会对其cost进行计算。

下图展示了APPLY_RULE task的算法，在APPLY_RULE::perform()方法中实现。Columbia中的实现方式与Cascades一致。

在找到binding后，RULE::condition()方法会被调用以决定这个rule是否可以实际被应用到该expression上。例如，一个将select push到join之下的rule要求具有兼容schema的condition。这个condition只有在binding之后才能被校验，因为input group的schema只有在binding之后才是可用的。

在rule被应用到multi-expression之后，multi-expression中对应的rule bit就会被置位，这样下一次同样的rule就不会被再次应用到该multi-expression上，因此可以避免重复工作。

4.2.3.5 O_INPUTS - Task to optimize inputs and derive cost of an expression

优化过程中，在一个implementation rule被应用之后，即，对于query tree中的一个节点考虑implementation 算法，优化过程会通过对implementation算法那的每一个input进行优化以推进。O_INPUTS task的目标是计算出一个physical multi-expression的cost。它会首先计算这个multi-expression的input的cost并将它们加到top operator的cost上。O_INPUTS类中的数据成员input_no，初始化时为0，它表明了哪个input已经被计算出了cost。这个task和其他task不一样的点在于它在调度起其他tasks后自身并不会停止。它会首先将自己push到stack中，然后调度下一个input的优化。当所有的input的cost都被计算完成，它就会计算整个physical multi-expression的cost。

这个task是我们在4.3章将会介绍的Columbia的剪枝技术的主要实现task。基于Cascades中的同样task，Columbia中的O_INPUTS重新设计了算法，并添加了剪枝相关的逻辑来实现Columbia中新出现的剪枝技术。

下图展示了O_INPUTS::perform()方法的伪代码，它实现了O_INPUTS task中的算法。

符号说明：

G：被优化的group

IG：G中expression的多种inputs

GLB：一个input group的Group Lower Bound，作为group的数据成员存储

Full winner：一个plan不为空的winner

InputCost[]：包含G的最优inputs的真实（或是lower bound）cost

LocalCost：正在被优化的top operator的cost

CostSoFar：LocalCost + 所有InputCost[]条目的sum

算法中有三个剪枝flag：Pruning、CuCardPruning、GlobepsPruning。优化器的使用者可以根据对Columbia中不同的剪枝技术的实验结果来设置这些flags。

四个例子可以作为Columbia的benchmarks。O_INPUTS算法使用不同的逻辑处理这四个case。在Cascades中，只处理case1和2。

Starburst - [!Pruning && !CuCardPruning]：不执行剪枝，为input groups生成所有的expressions，即，彻底展开input groups。
Simple Pruning - [Pruning && !CuCardPruning]：试图通过积极检查limits来避免input group的扩展。即，如果在优化过程中某个expression的CostSoFar大于了优化context中的upper bound，那么task就会中止不再进行后续的优化。在这种场景下，InputCost[]中的条目只会在input有一个针对优化context的winner时，存储input的winner cost。
Lower Bound Pruning - [CuCardPruning]：尝试尽可能的避免input group扩展。这个场景和simple pruning的区别在于：如果对于一个input group没有winner，当前场景会在InputCost[]条目中存储input group的GLB。此场景会假设Pruning flag是开启的，即，代码会在CuCardPruning为true时强制Pruning flag为true.
Global Epsilon Pruning - [GlobepsPruning]：如果一个plan的cost低于global epsilon value（GLOBAL_EPS），它会被认为是G的final winner，因此不再需要进一步的优化了。这个flag和其他的flag独立。它可以和其他三种情况结合在一起优化。

4.3 Pruning Techniques

在本章中，我们会讨论Columbia的两种剪枝技术。它们扩展了Cascades中的搜索算法并通过对search space的高效剪枝提升了search性能。和我们在4.2.3.5小节中介绍的一样，剪枝技术主要在O_INPUTS task中实现。

4.3.1 Lower Bound Pruning

动机：Top-down的优化器会在一些lower-level的plan生成之前为high-level physical plans计算cost。这些提前计算的cost会作为子优化的upper bounds。在许多场景下这些upper bounds可能会用于避免生成全部的expressions group。我们称之为剪枝。

由于Columbia的搜索过程是top-down且记忆化的，bounds可以用于对整个group进行剪枝。例如，假设优化器的输入是(A x B) x C。优化器会首先计算group[ABC]中一个plan的cost，假设是(A x LB) x LC，假设它的cost是5s。算法此时扩展了group[AB]，而没有在这计算5s cost的过程中考虑group[AC]或是[BC]。现在我们来考虑对group中的另一个expressions进行优化，假设为[AC] x [B]。假设group[AC]代表一个笛卡尔积，它的计算量巨大以至于将元组从[AC]复制到[ABC]就需要消耗多于5s。这意味着包含[AC]的plan用于不会是[ABC]的最优计划。在这个场景下，优化器不会生成[AC]中的所有计划，因此可以进行高效的剪枝。下图展示了对上面讨论的两个expressions进行优化后的search space。注意[AC]group没有被扩展。从另一方面来说，Starburst和其他的bottom-up优化器在开始对[ABC]的优化之前就对group[AB]、[AC]和[BC]进行了优化，因此失去了对多个plan剪枝的机会。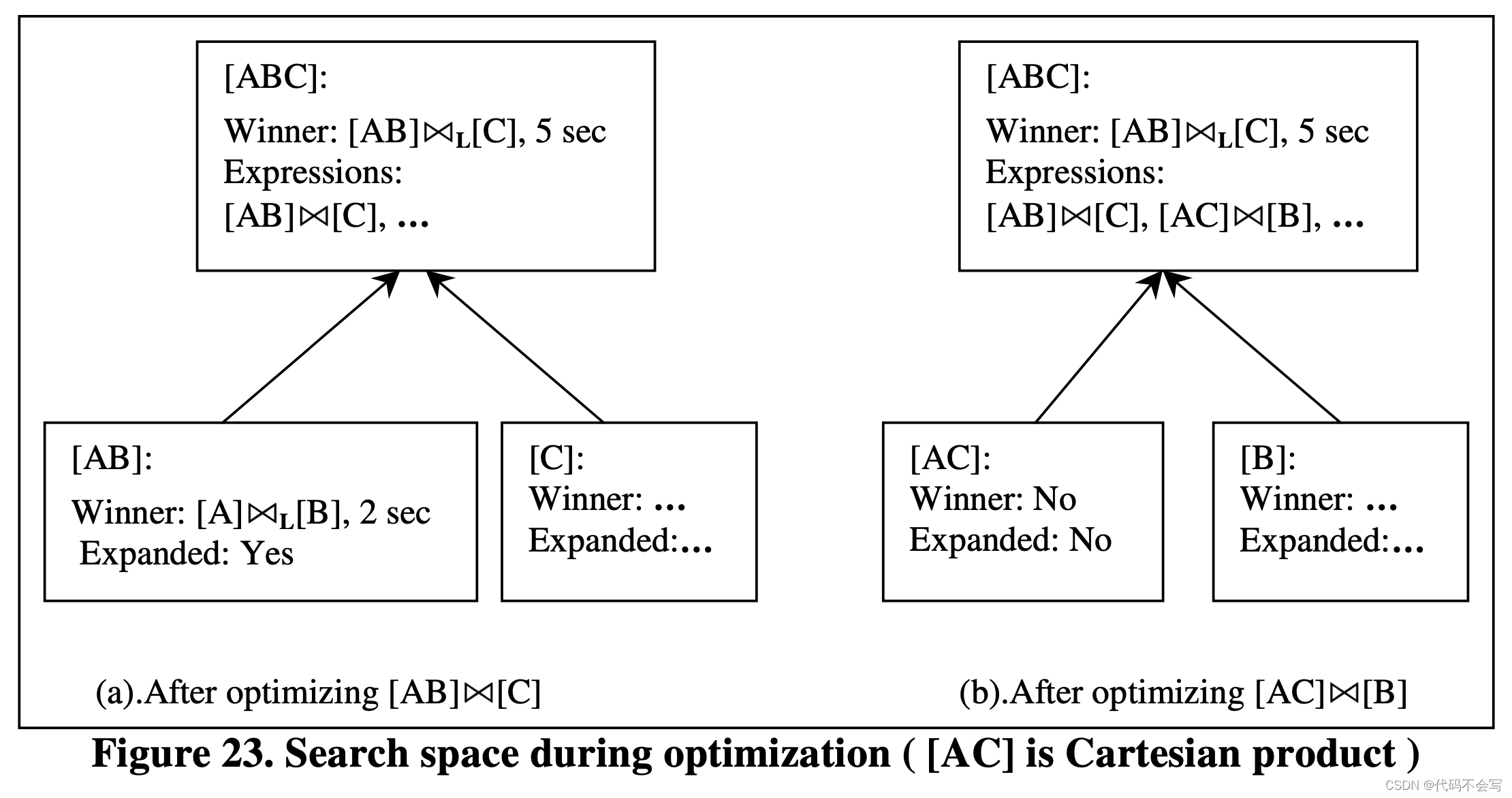

如果一个group G从不被枚举，我们就说它被剪枝了。一个剪枝后的group最后将只包含一个expression，即初始化的expression。Group剪枝可以飞铲购销：一个代表对k个tables进行join的group可能会包含2K-2个logical expressions，且一个group中的physical expressions通常会是logical expressions的两倍。

算法：在这一章节中我们会描述Columbia如何通过改进的优化算法来增加实现group剪枝的可能性。如下图所示，这个算法那是O_INPUTS task中的一部分，并且是Figure22中Note1的详细描述。

在上图中，(1)~(4)行计算了一个Expr的cost的lower bound。如果这个lower bound大于当前context中的upper bound，即Limit，那么当前路径可以直接返回，无需枚举任何input groups。这个算法和Cascades算法的区别在于，Cascades中没有line(4)的处理。

在Columbia中，一个group会有一个对应的group lower bound，它代表着将group的tuple复制出来和从group的tables中获取这些tuple的最小成本。这个group lower bound在对expressions的优化之前被计算并存储在group中，因为它只依赖于group的logical properties。Line(4)中包含了对于required properties没有最优plan的input的group lower bound，从而提高了Expr cost的lower bound，进而提高了group剪枝的可能性。

下图展示了当lower bound group剪枝发生时的场景。在这个场景中，Cascades算法将不会对group[BC]进行剪枝因为这个被优化expression的lower bound cost仅仅是当前expression的operator的cost和input中的winner（如果有的话）的cost之和。在这个场景下，它等于 1+2+0=3，并且没有比context中的upper bound更高。所以group[BC]还是被扩展了。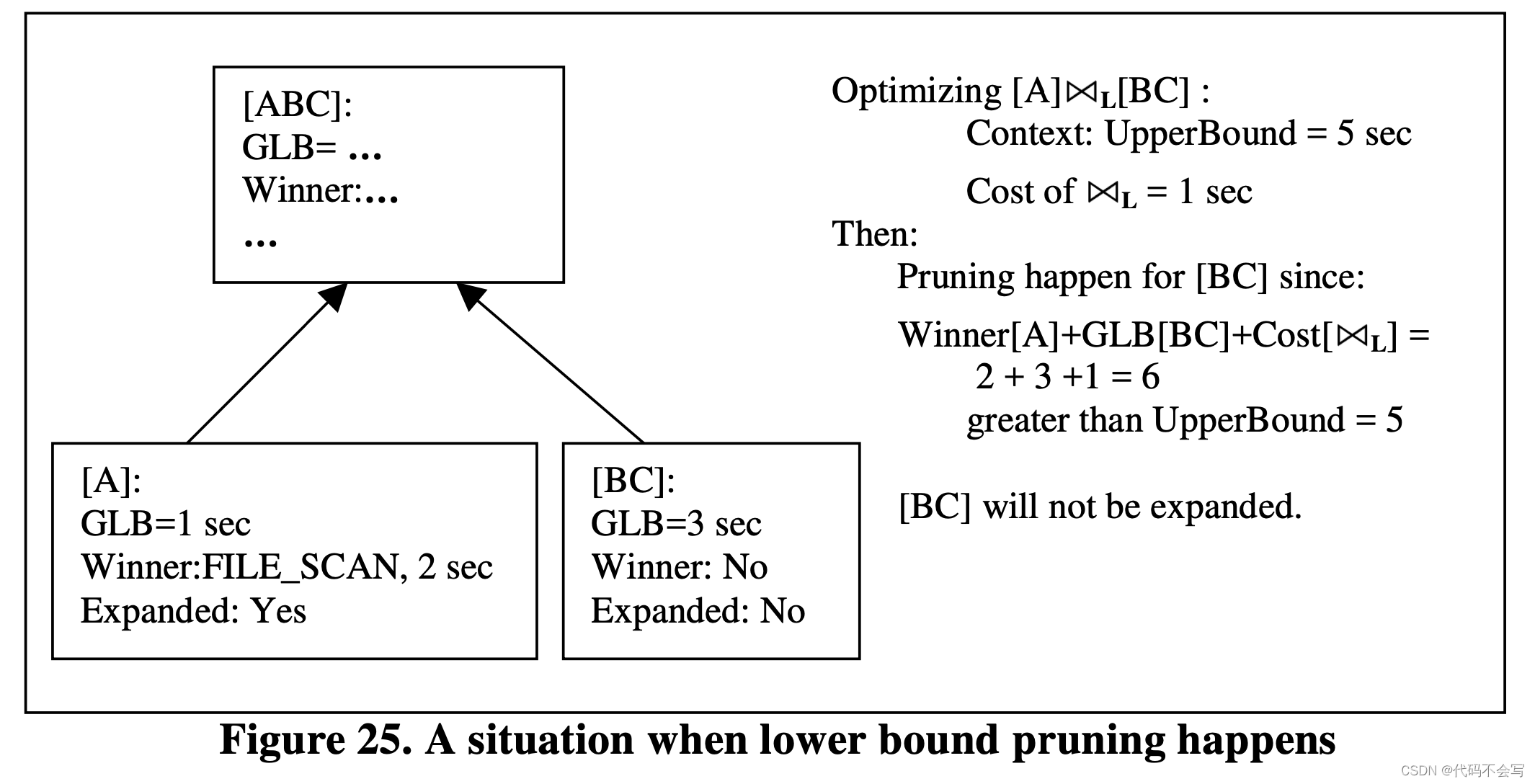

Lower Bound Group剪枝是安全的，即，优化器使用这个剪枝技术来生产最优plan。因为我们只会在一个set中的lower bound cost大于其他plan的cost时去对这个set的plans进行剪枝，并且我们在4.1.2.3中证明了我们使用的bound是一个lower bound。

4.3.2 Global Epsilon Pruning

动机：满足的概念起源于经济学。其理念是，从理论上来讲，经济系统受法律的只配，法律要求每个人在满足某些约束条件的前提下，优化自己的满意度。实际中人们却不会这样行动：他们满足于几乎满足约束条件的最优解。这个行为被称为满足。一种看待满足的方法是想想有一些常量的epsilon，并且所有事物都在epsilon中被优化/满足。满足的想法是下面这个想法的动机。

Global Epsilon Pruning：一个plan如果它的cost（with epsilon）和最优plan的cost足够接近，就可以被认为是一个group的final winner。一旦这样一个winner被宣布了，group就不再需要进一步的优化了，因此可能会对search space进行剪枝。例如，假设我们在优化group[ABC]，我们会计算在group中获取到的第一个plan的cost，假设为 (AxB)xC且它的cost为5s。如果我们选择的epsilon是6s，即，我们认为一个小于6s的plan就是一个final winner。尽管它不是最优的，但我们对它已经满足了。因此cost为5s的plan (AxB)xC被认为是group[ABC]的final winner，因此针对这个group就不会在做进一步的搜索了。换句话说，对于group[ABC]的搜索已经结束，尽管我们甚至都没有扩展group[ABC]。通过这个方法可以对search space中的许多expressions进行剪枝。

这种剪枝技术被称为Global Epsilon Pruning，因为这个epsilon在会在整个优化过程中被全局使用，而不是只针对一个指定group优化进行本地使用。

算法：选择一个全局的参数Globeps >0。遵循常用的优化算法，除非一个group中声明了final winner，如果发现了一个满足下面限制条件的plan：cost(plan) < Globeps。

进入这个group中的winner并标记search context为done，来表示这个group不再需要进一步的search了。

这个算法是在O_INPUTS task中实现的，对应于Figure22中的Note2。在一个优化expressions的cost被计算后，如果global epsilon pruning的flag被置位，就会用这个cost和global epsilon进行比较。如果cost小于epsilon那么search就会结束。

显然，Global Epsilon Pruning不会输出一个最优plan。但从某种意义上说，到绝对最优的距离是有限的。

定理：假设“absolute-optimum”代表常规优化的结果，“Globeps-optimum”代表使用Global Epsilon Pruning优化的结果。如果绝对最优有N个节点，它们的cost都小于Globeps，那么Globeps-optimum的cost和absolute-optimum相差最多：N*Globeps

证明：开始在absolute-optimum上执行一个深度优先的搜索，但使用Global Epsilon Pruning来替换first plan的每一个最优input，保证其cost小于Globeps，如果存在的话。N个这样的最优input会被替换。用P标识这个过程的结果。因为P在大多数的N个input中和absolute-optimum具有差值，最多为Globeps，那么我们就有

cost(P) - cost(absolute-optimum) < N*Globeps

由于search space中P是被Global Epsilon Pruning算法定义的，我们必须满足（？？？）

cost(Globeps-optimum) < cost(P)

不同的eplisons值会极大地影响剪枝。一个非常小的eplison可能完全不会产生剪枝因为group中所有plan的cost都大于这个eplison。另一方面，一个大的eplison会剪枝掉大量的plan，但可能会输出一个和最优plan差距极大的plan。因为剪枝技术重度依赖于我们选择的eplison，上面的定理给了我们一个如何选择eplison的想法。例如，假设我们想去优化一个10 table的join。我们估计这个join的最优计划的cost是100s，最优计划有20个节点，我们还假设与最优计划的距离为10s的计划是可以接受的。根据定理，我们可以有一个Globeps-optimum计划，其cost与最优计划的cost相差最多20*Globeps = 10，这是可以接受的。因此我们可以选择值为0.5的global epsilon。

怎么估计的最优计划cost 100s ？

在第五章中提到，我们可以首先不使用eplison pruning将服务运行一段时间，收集优化器生成的最佳执行计划的cost，然后再来指导eplison pruning。

4.4 Usability in the Columbia Optimizer

除了在前面章节中描述的Cascades上提高了效率之外，在Columbia中还通过使用window interface与用户交互并支持持续的跟踪信息来提高可用性。本节介绍Columbia对Cascades的可用性改进。

4.4.1 Windows Interface

交互界面，略

4.4.2 Tracing of the optimizer

由于优化的行为是非常复杂的，想要debug或是验证优化过程是非常困难的。在优化过程中跟踪优化器提供的信息是一种能让用户了解优化过程并了解优化器工作方式的一种方法。Columbia优化了Cascades中的跟踪机制以为用户提供易读的，可控的优化信息。

优化的跟踪可能包括：

优化器的输入内容：需要被优化的quey、catalog、cost model和优化器中的rule set。通过查看这些信息，我们可以知道优化器在做什么。
task stack中的内容：它被称为OPEN stack。这个stack包含需要被调度的task。每一次一个task从stack的顶部移除并被执行。通过查看OPEN stack，我们可以知道优化器是如何工作并调度这些优化task的。
每个task的执行细节：跟踪一个特定task的执行细节
每一个task执行后的search space内容：在每一个task被执行后，search space可能会发生变更，因为更多的expressions或是winner可能会被加入到search space中。这个信息跟踪每个task的结果。
final search space的内容：在优化完成后，final search space会被打印出来。通过查看final search sapce，用户可以找到优化器的最终状态。例如，每个group中生成了多少expressions。

上面的信息是非常具有扩展性的。一些时候用户只对跟踪结果中的一部分感兴趣。Columbia为优化器提供了设置跟踪选项的控制。跟踪控制有两组设置：

Trace To：用户可以选择跟踪信息输出目标，到文本文件、窗口等。
Trace Content：这个选项允许用户选择感兴趣的部分跟踪内容。略

Chapter 5. Result and Performance

略

Chapter 2. Conclusions and Future works

Columbia基于Cascades的基础上采用了集中工程技术来提高效率，这些技术减少了优化过程中对CPU和内存资源的消耗：

用户消除重复expressions的fast hash function
group中logical和physical expressions的分离
小而紧凑的数据结构
优化groups和inputs的高效算法
处理enforcer的高效方式

Columbia优化器实现了两种剪枝技术。通过使用lower bound group pruning，search space在没有对规划质量妥协的情况下极大地进行了剪枝。一个group lower bound可以在group被优化之前被快速获取到。Lower bound超过search limit（upper bound）的group可以安全地被剪枝。Columbia优化器中用到的另一个剪枝技术是global epsilon pruning。这个技术可以通过生成可接受的近似于最优的解决方案来对search space进行剪枝。当一个足够接近于最优解决方案的方案被找到时，优化目的就达到了。对这种剪枝技术的有效性和准确性的分析展示，通过消息选择epsilon值，优化可以非常高效并仍然能生成可接受的解决方案。

Columbia优化器还有很多额外的优化工作需要去做。当前优化器仍然使用了大量的内存来优化大查询。在优化非常大的查询，例如包含超过16个表的星型查询时，内存使用可能会变得令人望而却步。类似于周期性垃圾收集和内存共享的技术可能有助于最小化内存使用。这值得进一步的系统探查。

另一个重要的问题是优化器解决方案的正确性。很难证明优化器产生的是最有计划还是由于编程bug产生的是次优计划，特别是在优化大型查询时。尽管在Columbia优化器中添加了跟踪工具，但优化的验证和调试仍然是一项复杂且耗时的任务。一些可视化工具或快速验证工具对于验证优化器很有用。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/IT小白/article/detail/550519