shor算法

目录

1.RSA算法

 2.shor算法流程

3.shor算法的个人理解

---

1.RSA算法

RSA作为公钥加密，它的安全性主要依赖于大数分解的难度。根据整数唯一分解定理我们可以知道p和q就是n的唯一的素因子分解形式，其中n是正奇合数，p、q均为素数。利用经典方式将n分解成两个素数的乘积形式对于大数而言是很困难的，但是根据shor算法我们可以解决这个难题。

 2.shor算法流程

在介绍shor算法之前，我们需要知晓order-finding算法是什么（其实就是求阶r的一个过程），过程如下（后期填坑） ：

我们可以将n的因式分解问题归纳到求阶问题，我们先来介绍两个重要的定理来说明因式分解和求阶问题之间的关系。

定理1：假设N是一个L比特的合数（除去1和自身之外，还能够被其他的数整除，0除外），若有x*x=1(mod N)，其中x是N的非平凡解，满足x≠-1 mod N=N-1，并且x≠1 mod N=1，那么gcd(x-1,N)和gcd(x+1,N)中至少有一个数是N的非平凡因子。

我们分析一下为什么说这两个最大公约数中至少有一个数是N的非平凡因子。

 但是怎么找到使得方程x² （mod N) =1的非平凡解x呢？

我们随机地在小于N-1的整数中选取x,要求x和N是互素的，如果我们能够找到使得x的r次方模N成立的r，其中r是偶数，并且x的二分之r次方模N不等于正负1，那么我们就说x的二分之r次方模N是方程x² (mod N) =1的一个非平凡解，结合定理一，我们利用欧几里得算法可以得到N的非平凡因子，至少是一个。

 定理2：

 

从定义1我们可以看出，如果 p=gcd(x-1,N) ,q=gcd(x+1,N),p、q都是N的非平凡因子，且均为素数，那么我们就完成了N的因子分解，对应于我们在第一部分所讲的n的分解。但是如果p、q都是N的非平凡因子，但不都是素数，说明此时还是可以继续对非素数的p(或q)进行因子分解，直至将N表示为多个素因子乘积的形式。

从定理2我们可以看出来,N的素因子个数m越多，那么成功的概率也就越高。我们能够找到r是偶数，并且x的（r/2）次方 mod N≠1的概率至少是0.5，随着N素因子个数的增加，这种成功概率是越大的。

阶r的定义是使得使得x的r次方mod N=1的最小正整数,如果x的（r/2）次方 mod N=1,r就不是阶了，所以x的（r/2）次方 mod N≠1。

根据定理1我们可以看出对于1<x mod N<N-1,在定理2中，我们也要确保1<（x的r/2次方） mod N<N-1。同时我们要注意，在定理2中，x是和N互质的。

下面正式介绍如何将因子分解问题规约到求阶问题上：

输入：合数N

输出：N的不平凡因子（根据定理1，我认为至少得到一个N的非平凡因子）

过程：

（1）先判断N是否为偶数，若是，返回因子2，end。否则，进行（2）；

（2）判断N是否为a的b次幂（a>=1,b>=2）,若是，返回因子2,end。否则，进行（3）；

（3）1<=x<=N,我们随机选取x，计算gcd(x,N)=m,如果m≠1，返回m，end。否则进行（4）；

  (4) 随机选取与N互质的x，利用order-finding算法计算x 模N的阶r;

说明: 选取的x可能并不能找到满足条件的r，这时候就需要我们重新选取x，在进行步骤（4）

（5）得到r,若r满足下列要求，则至少得到一个N的非平凡因子：

 

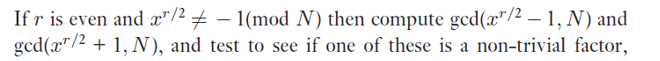
如果r不满足上述要求（r为偶数，并且x的（r/2）次幂是N的非平凡解），那么算法是失败的。所以由此看来，算法的关键在于步骤（4）找到的r是否满足条件。

上述五个步骤，只有步骤（4）调用求阶子程序，涉及量子过程。算法（1）（2）要么返回一个因子，要么保证N是一个包含多于一个素因子的奇数。步骤（3）要么返回一个因子，要么从1~N-1中随机抽取x，基于步骤3，选择和N互质的x，求阶r，步骤5结束算法。

3.shor算法的个人理解

在shor算法中，我们只是说N是个合数，如果对于33=3*11这种形式，p和q都是素数，根据定理2，我们将33表示成了两个素数乘积的形式，这个形式是唯一的。但是对于45=3*15=5*9，我们知道由于r的不同，shor算法得到的只是3*15或者5*9这两种形式的某一种。

如果要将N表示为多个素数因子乘积的唯一形式，我们还要对15（或者9）继续进行因式分解，此时N=15（或者9）,不过此时N的范围相较于最初N=45已经缩小了。

shor算法并不能保证我们的每次运行都可以得到正确的结果。首先，相位估计的结果可能会给出s/r一个糟糕的估计，但是这样的概率最多是ε，我们是可以通过调整线路的规模尽可能地降低这个误差的。第二种情况是s和r之间存在公因子，这时候我们得到的r'是r的一个因子，并不是r本身。

结合黄皮书盒子5.4来看，以0.25的概率得到0,512,1024,1536，在这个盒子中，假设的是l=1536,得到r=4，但是如果l=1024，得到r'=2（是4的因子）,但是此时x的r的阶次方 mod N ≠1，所以2不是阶。

说到这里我们不禁要思考，如果我们求得的阶r'是真实r的因子我们怎么解决这个问题，有三种方法：

（1）选择和r互质的s;

  (2) 利用 r=r' *(r/r'),其中r'是r的因子，详细见黄皮书第212页；

（3）将相位估计多重复几次，寻找r'的最小公倍数，结合盒子5.4解释如下：