备战秋招60天算法挑战，Day4

题目链接： https://leetcode.cn/problems/search-in-rotated-sorted-array/

视频题解： https://www.bilibili.com/video/BV1tz421r7xC/

LeetCode 33.搜索旋转排序数组

题目描述

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

举个例子：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4
1
2

视频题解

搜索旋转排序数组

思路解析

这道题和「LeetCode 153. 寻找旋转排序数组中的最小值」思路基本一致，主要的差异有两点：

1. 本题的target有可能是不存在的。
2. 本题的target是给定的，153中的最小值是未知的。

因为题目要求时间复杂度为 O(log n)，所以这道题目的核心思想还是二分查找。初始化索引L = 0，R = nums.size - 1，M = (L + R) / 2，假设目标target = 0。

旋转排序数组有个特点，只需要比较区间两个边界的元素的大小，就可以知道区间是否是单调的。比如，如果nums[L] < nums[M]，那么区间[L, M)就是升序的。

我们针对区间[L, M)为升序区间和(M, R]为升序区间两种情况分别讨论。

1. [L, M)为升序区间。

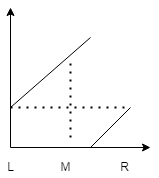
这个时候target如果在升序区间[L, M)范围，后面就只需在升序区间查找R = M - 1。否则L = M + 1。

2. (M, R]为升序区间。

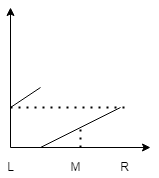
这个时候target如果在升序区间(M, R]范围，后面就只需在升序区间查找L = M + 1。否则R = M - 1。

C++代码

class Solution {
public:
    int search(vector<int>& nums, int target) {

        int nums_len = nums.size();
        int left = 0, right = nums_len - 1;
       
        while (left <= right) {
            int mid = (left + right)/2;
            //找到target
            if (target == nums[mid]) {
                return mid;
            } 
            //[left, mid)有序
            if (nums[left] <= nums[mid]) {
                //target在左侧有序范围内
                if (nums[left] <= target && target < nums[mid]) {
                    right = mid - 1;
                //target在右侧区间
                } else {
                    left = mid + 1;
                }
            //(mid, right]有序
            } else {
                //target在右侧有序范围内
                if (nums[mid] < target && target <= nums[right]) {
                    left = mid + 1;
                //target在左侧区间
                } else {
                    right = mid - 1;
                }
            }

        }
        return -1;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

java代码

class Solution {
    public int search(int[] nums, int target) {
        int numsLen = nums.length;
        int left = 0, right = numsLen - 1;

        while (left <= right) {
            int mid = (left + right) / 2;
            //找到target
            if (target == nums[mid]) {
                return mid;
            }
            //[left, mid)有序
            if (nums[left] <= nums[mid]) {
                //target在左侧有序范围内
                if (nums[left] <= target && target < nums[mid]) {
                    right = mid - 1;
                //target在右侧区间
                } else {
                    left = mid + 1;
                }
            //(mid, right]有序
            } else {
                //target在右侧有序范围内
                if (nums[mid] < target && target <= nums[right]) {
                    left = mid + 1;
                //target在左侧区间
                } else {
                    right = mid - 1;
                }
            }
        }
        return -1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

python代码

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        numsLen = len(nums)
        left, right = 0, numsLen - 1

        while left <= right:
            mid = (left + right) // 2
            #找到target
            if target == nums[mid]:
                return mid
            #[left, mid)有序
            if nums[left] <= nums[mid]:
                #target在左侧有序范围内
                if nums[left] <= target < nums[mid]:
                    right = mid - 1
                #target在右侧区间
                else:
                    left = mid + 1
            #(mid, right]有序
            else:
                #target在右侧有序范围内
                if nums[mid] < target <= nums[right]:
                    left = mid + 1
                #target在左侧区间
                else:
                    right = mid - 1
        return -1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

复杂度分析

时间复杂度： 使用了二分查找，故时间复杂度为 O(log n)，其中n为nums的长度。

空间复杂度： 这个过程就使用了有限个整型变量，故空间复杂度为O(1)。