热门标签
当前位置: article > 正文
数据结构之链表(java语言实现)_java实现链表
作者：Li_阴宅 | 2024-07-01 18:24:55
赞
踩
java实现链表
链表的底层储存结构：
相对于数组这一需要连续、足够大空间的数据结构，链表只需要利用“指针”将一组零碎的空间(在链表中称之为节点)串联起来，这样就可以避免在创建数组时一次性申请过大的空间二导致有可能创建失败的问题!!!
同时比较两种数据结构我们易发现：
1.数组“擅长”按照下标随机访问的相关操作
2.链表“擅长”插入、删除操作
在这里插入图片描述
链表的定义和操作：
在链表中为了把每个节点串联起来，每个节点除了存储数据本身外，还需要额外的空间存储下一个节点的地址。我们把记录下一个节点地址的指针称为next指针（后继指针）。
在一个链表中我们称链表的第一个节点为头节点用于存储链表的基地址，称链表的最后一个节点为尾节点，其next指针指向空地址（在Java中空地址用null表示）。
对于链表的定义Java语言代码实现如下:
public class LinkedList{
public class Node {
public int data; //假设节点储存的数据类型为int
public Node next;
}
private Node head = null;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
我们易知对于数组的插入和删除都会涉及到数据的搬移所以时间复杂度为O(N)，但是由于链表并不是连续的储存空间，所以我们只需要操作操作链表节点的next指针就可以实现插入，删除操作，其相对数组的删除插入操作效率更高为O(1)。其查找，删除，插入的代码实现如下:
//查找 public Node find(int value) { Node p = head; while (p != null && p.data != value) { p = p.next; } return p; } //插入 //其中b节点为前驱节点，x为待插入节点 void insert(Node b, Node x) { //待插入的节点在链表头部 if (b == null) { x.next = head; head = x; } elas { x.next = b.next; b.next = x; } } //删除 //a为b的前驱节点 void remove(Node a, Node b) { if (a == null) { head = head.next; } else { a.next = a.next.next; //相当去操作a.next = b.next; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
但是我们看删除函数remove我们之所以能够达到O(1)的时间复杂度是因为我们已知其前驱节点。而由于链表的空间地址是不连续的所以计算机不能想数组那样通过寻址公式直接在基地址的基础上算出第k个节点的地址，所以对于单链表的删除需要先遍历到其前驱节点在实现删除，时间复杂度为O（N）。
链表的变形结构：
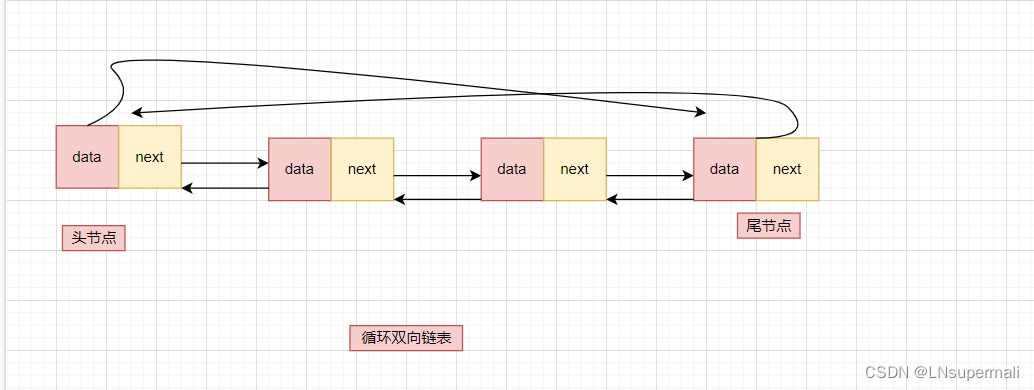
除较简单的单链表之外还有：循环链表、双向链表、循环双向链表。
1.循环链表:即链表的尾节点的next指针指向了链表头构成了一个环；
2.双向链表：在每个节点都存在一个前驱指针(pre)指向当前节点的上节点。
3.循环双向链表
对于双向链表的定义Java代码实现如下：
public class LinkedList{
public class Node {
public int data; //假设节点储存的数据类型为int
public Node next;
public Node prev;
}
private Node head = null;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
我们易发现由于多了prev指针双向链表要比单链表占用更多的内存，不过这样就能在O(1)时间复杂度的情况下找到某个节点的前驱节点，也是因为这个特点使得双向链表在某些情况下对节点的删除喝插入比单链表要更加简便！我们对删除做出两种常见的分类：
1.按照指定的值进行删除
2.按照指定的指针指向删除节点
对于第一种情况，不论是单链表还是双向链表我们都需要先从表头遍历比较时间复杂度均为：O(N)
//单链表中删除指定的值 public void remove(int value) { Node q = head; Node p = null; //q的前驱节点 while (q != null && q.next != null) { p = q; q = q.next; } if (q != null) { //找到值等于val的节点q if (p == null) { //q是头节点 head = q.next; } else { p.next = q.next; } } } //在双向链表中删除值等于value的节点 public void remove(int value) { Node q = head; while (q != null && q.data != value) { q = q.next; } if (q != null) { if (q.prev == null) { head = head.next; } else { q.prev.next = q.next; } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
但是针对于第二种情况(删除给定指针指向的节点)对于单链表，尽管我们已经找到要删除的节点，但是单链表中是没有储存前驱节点的所以我们还要从头开始遍历链表直到p.next = q为止，所以其的时间复杂度还是O(N),但是双向链表本身储存了其前驱指针，所以我们就可以省去再一次的遍历找其前驱的操作，所以其时间复杂度为O(1)
//单链表中删除节点q void remove() { if (q == null) { return; } if (head == q) { head = q.next; return; } Node p = head; while (p != null && p.next != q) { p = p.next; } if (p.next != null) { p.next = q.next; } } //在双向链表中删除值节点q void remove(Node q) { if (q == null) { return; } if (q.prev == null) { //q是头节点 head = q.next; return; } q.prev.next = q.next; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
实践操作：
读者可以尝试自己用链表完成如下操作：
1.单链表的翻转（写完可以尝试完成力扣206题）
2.链表中环的检测（写完可以尝试完成力扣141题）
3.两个有序链表的合并(写完可以尝试完成力扣21题)
4.删除链表倒数第k个节点（写完可以尝试完成力扣19题）
5.寻找链表的中间节点(有一个规律)（使用快慢指针同时讨论链表长度为奇数喝偶数时的情况)
部分代码实现：
package DataStructures.linkedlist_; /** * @author: * @data: * @description: */ public class SinglyLinkedList { /** * 1)单链表的插入、删除、查找操作 * 2)链表中储存的是int类型的数据 */ private Node head = null; public Node findByValue(int value) { Node p = head; while (p != null && p.data != value) { p = p.next; } return p; } public Node findByIndex(int index) { Node p = head; int pos = 0; while (p != null && pos != index) { p = p.next; pos++; } return p; } //无头节点 //表头部插入 //这种操作将输入的顺序相反，逆序 public void insertToHead(int value) { Node newNode = new Node(value, null); insertToHead(newNode); } public void insertToHead(Node newNode) { if (head == null) { head = newNode; } else { newNode.next = head; head = newNode; } } //顺序插入 //链表的尾部插入 public void insertTail(int value) { Node newNode = new Node(value, null); //空链表，可以插入新节点作为head，也可以不操作 if (head == null) { head = newNode; } else { Node q = head; while (q.next != null) { q = q.next; } q.next = newNode; } } public void insertAfter(Node p, int value) { Node newNode = new Node(value, null); insertAfter(p, value); } public void insertAfter(Node p, Node newNode) { if (p == null) return; newNode.next = p.next; p.next = newNode; } public void insertBefore(Node p, int value) { Node newNode = new Node(value, null); insertAfter(p, newNode); } public void insertBefore(Node p, Node newNode) { if (p == null) return; //如果p为头节点。则头插 if (head == p) { insertToHead(newNode); return; } Node q = head; while (q != null && q.next != p) { q = q.next; } if (q == null) { return; } newNode.next = p; q.next = newNode; } public void deleteByNode(Node p) { if (p == null || head == null) return; if (p == head) {//待删除的为头节点 head = head.next; return; } Node q = head; while (q != null && q.next != p) { q = q.next; } if (q == null) { return; } q.next = p.next; } public void deleteByValue(int value) { if (head == null) return; Node p = head; Node q = null; while (p != null && p.data != value) { q = p; p = p.next; } if (p == null) { return; } if (q == null) { head = head.next; } else { q.next = q.next.next; } // 可删除指定重复value的代码 /* if (head != null && head.data == value) { head = head.next; } Node pNode = head; while (pNode != null) { if (pNode.next.data == data) { pNode.next = pNode.next.next; continue; } pNode = pNode.next; } */ } public void printAll() { Node p = head; while (p != null) { System.out.print(p.data + " "); p = p.next; } System.out.println(); } //判断true or false public boolean TFResult(Node left, Node right) { Node l = left; Node r = right; boolean flag = true; System.out.println("left_:" + l.data); System.out.println("right_:" + r.data); while (l != null && r != null) { if (l.data == r.data) { l = l.next; r = r.next; continue; } else { flag = false; break; } } System.out.println("什么结果"); return flag; /* if (l == null && r == null) { System.out.println("什么结果"); return true; } else { return false; } */ } // 判断是否回文 public boolean palindrome() { if (head == null) { return false; } else { System.out.println("开始执行找到中间节点"); Node p = head; Node q = head; if (p.next == null) { System.out.println("只有一个元素"); return true; } while (q.next != null && q.next.next != null) { p = p.next; q = q.next.next; } System.out.println("中间节点" + p.data); System.out.println("开始执行奇数节点的回文判断"); Node leftLink = null; Node rightLink = null; if (q.next == null) { //此时p一定为整个链表的中点，且节点数目为奇数 rightLink = p.next; leftLink = inverseLinkList(p).next; System.out.println("左边第一个节点" + leftLink.data); System.out.println("右边第一个节点" + rightLink.data); } else { //p q均为中点 rightLink = p.next; leftLink = inverseLinkList(p); } return TFResult(leftLink, rightLink); } } //带头节点的链表翻转 public Node inverseLinkList_head(Node p) { // Head 为新建的一个头节点 Node Head = new Node(9999,null); // p 为原来整个链表的头节点，现在Head指向 整个链表 Head.next = p; /* 带头结点的链表翻转等价于 从第二个元素开始重新头插法建立链表 */ Node Cur = p.next; p.next = null; Node next = null; while (Cur != null) { next = Cur.next; Cur.next = Head.next; Head.next = Cur; System.out.println("first " + Head.data); Cur = next; } // 返回左半部分的中点之前的那个节点 // 从此处开始同步向两边比较 return Head; } // 无头节点的链表翻转 public Node inverseLinkList(Node p) { Node pre = null; Node r = head; System.out.println("z----" + r.data); Node next = null; while (r != p) { next = r.next; r.next = pre; pre = r; r = next; } r.next = pre; // 返回左半部分的中点之前的那个节点 // 从此处开始同步像两边比较 return r; } public static Node CreateNode(int value) { return new Node(value, null); } //Node public static class Node { private int data; private Node next; public Node(int data, Node next) { this.data = data; this.next = next; } public int getData() { return data; } } public static void main(String[] args) { SinglyLinkedList link = new SinglyLinkedList(); System.out.println("hello"); //int data[] = {1}; //int data[] = {1,2}; //int data[] = {1,2,3,1}; //int data[] = {1,2,5}; //int data[] = {1,2,2,1}; // int data[] = {1,2,5,2,1}; int data[] = {1,2,5,3,1}; for (int i = 0; i < data.length; i++) { //link.insertToHead(data[i]); link.insertTail(data[i]); } // link.printAll(); // Node p = link.inverseLinkList_head(link.head); // while (p != null) { // System.out.println("aa" + p.data); // p = p.next; // } System.out.println("打印元始:"); link.printAll(); if (link.palindrome()) { System.out.println("回文"); } else { System.out.println("不是回文"); } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 248
- 249
- 250
- 251
- 252
- 253
- 254
- 255
- 256
- 257
- 258
- 259
- 260
- 261
- 262
- 263
- 264
- 265
- 266
- 267
- 268
- 269
- 270
- 271
- 272
- 273
- 274
- 275
- 276
- 277
- 278
- 279
- 280
- 281
- 282
- 283
- 284
- 285
- 286
- 287
- 288
- 289
- 290
- 291
- 292
- 293
- 294
- 295
- 296
- 297
- 298
- 299
- 300
- 301
- 302
- 303
- 304
- 305
- 306
- 307
- 308
- 309
- 310
- 311
- 312
- 313
- 314
- 315
- 316
- 317
- 318
- 319
- 320
- 321
- 322
- 323
- 324
- 325
- 326
- 327
- 328
- 329
- 330
- 331
力扣刷题中的常用操作(单链表)：
package DataStructures.linkedlist_; import java.util.LinkedList; /** * @author: ln * @data: * @description: */ public class Test { public static void main(String[] args) { // Create a LinkedList LinkedList<Integer> list = new LinkedList<>(); // Add element // Time Complexity: O(1) list.add(1); list.add(2); list.add(3); // [1,2,3] System.out.println(list.toString()); // Insert element // Time Complexity: O(N) list.add(2,99); // [1,2,99,3] System.out.println(list.toString()); // Access element // Time Complexity: O(N) int element = list.get(2); // 99 System.out.println(element); // Search element // Time complexity: O(N) int index = list.indexOf(99); // 2 System.out.println(index); // Update element // Time Complexity: O(N) list.set(2,88); // [1,2,88,3] System.out.println(list.toString()); // Length // Time Complexity: O(1) int length = list.size(); // 4 System.out.println(length); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
力扣题目推荐：
对于初学的小伙伴们可以先尝试完成如下两题:(建议初学者可以跟着b站up主–"爱学习的饲养员"学习数据结构的基础和刷题常用操作)
1.力扣203题移除链表元素
2.力扣206题反转链表(重点)
注：本笔记主要来自于对《数据结构与算法之美》–王争，一书的整理笔记，若有侵权问题，请第一时间联系作者!!!
声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/Li_阴宅/article/detail/777265
推荐阅读
相关标签
