数据结构：栈 （leetcode 例题 【简】【中】【难】）_1、整数 z:表示当前回合得分为 z; 2、“add”:表示当前回合得分为前两次得分之和;

例一  棒球比赛（leetcode 682) 【简单】

https://leetcode-cn.com/problems/baseball-game/https://leetcode-cn.com/problems/baseball-game/题目描述：

你现在是一场采用特殊赛制棒球比赛的记录员。这场比赛由若干回合组成，过去几回合的得分可能会影响以后几回合的得分。

比赛开始时，记录是空白的。你会得到一个记录操作的字符串列表 ops，其中 ops[i] 是你需要记录的第 i 项操作，ops 遵循下述规则：

1、整数 x - 表示本回合新获得分数 x
2、"+" - 表示本回合新获得的得分是前两次得分的总和。题目数据保证记录此操作时前面总是存在两个有效的分数。
3、"D" - 表示本回合新获得的得分是前一次得分的两倍。题目数据保证记录此操作时前面总是存在一个有效的分数。
4、"C" - 表示前一次得分无效，将其从记录中移除。题目数据保证记录此操作时前面总是存在一个有效的分数。
请你返回记录中所有得分的总和。

示例1：

示例2：

 题目分析：

很典型的栈结构存储，将数据按要求放进去即可。

值得注意的是将 string 转换成 int 类型，需要用 istringstream 处理。

操作如下：

/*将字符串a转换成整型x*/
 
string a;
int x;
 
istringstream is(a);
 
is >> x; //完成转换

题解代码：

class Solution {
public:
    int calPoints(vector<string>& ops) {
         stack<int> aa;
 
         for(int i=0;i<ops.size();i++){
             if(ops[i]=="C"){
                 aa.pop();
             }else if(ops[i]=="D"){
                 auto xx=aa.top()*2;
 
                 aa.push(xx);
             }else if(ops[i]=="+"){
                 int q=aa.top();
                 aa.pop();
                 int p=aa.top();
 
                 int qp=q+p;
                 aa.push(q);
                 aa.push(qp);
             }else{
                 int x;
                 istringstream is(ops[i]);
                 is>>x;
                 aa.push(x);
             }
         }
 
         int count=0;
         while(!aa.empty()){
             count+=aa.top();
 
             aa.pop();
         }
 
         return count;
    }
};

例二  每日温度（leetcode 793) 【中等】

https://leetcode-cn.com/problems/daily-temperatures/https://leetcode-cn.com/problems/daily-temperatures/题目描述：

请根据每日气温列表 temperatures ，请计算在每一天需要等几天才会有更高温度。如果气温在这之后都不会升高，请在该位置用 0 来表示。

示例1：

示例2：

示例3：

题目分析：

遍历整个数组，如果栈不空，且当前数字大于栈顶元素，那么如果直接入栈的话就不是递减栈，所以需要取出栈顶元素，由于当前数字大于栈顶元素的数字，而且一定是第一个大于栈顶元素的数，直接求出下标差就是二者的距离。

继续看新的栈顶元素，直到当前数字小于等于栈顶元素停止，然后将数字入栈，这样就可以一直保持递减栈，且每个数字和第一个大于它的数的距离也可以算出来。

题解代码：

class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& temperatures) {
           int n=temperatures.size();
 
           vector<int> xx(n,0);
           stack<int> aa;
 
           for(int i=0;i<n;i++){
               while(!aa.empty()&&temperatures[i]>temperatures[aa.top()]){
                   int q=i-aa.top();
                   xx[aa.top()]=q;
 
                   aa.pop();
               }
               
               aa.push(i);
           }
 
           return xx;
    }
};

例三  接雨水 （leetcode 42) 【困难】

https://leetcode-cn.com/problems/trapping-rain-water/https://leetcode-cn.com/problems/trapping-rain-water/题目描述：

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例1：

示例2：

 

 题目分析：

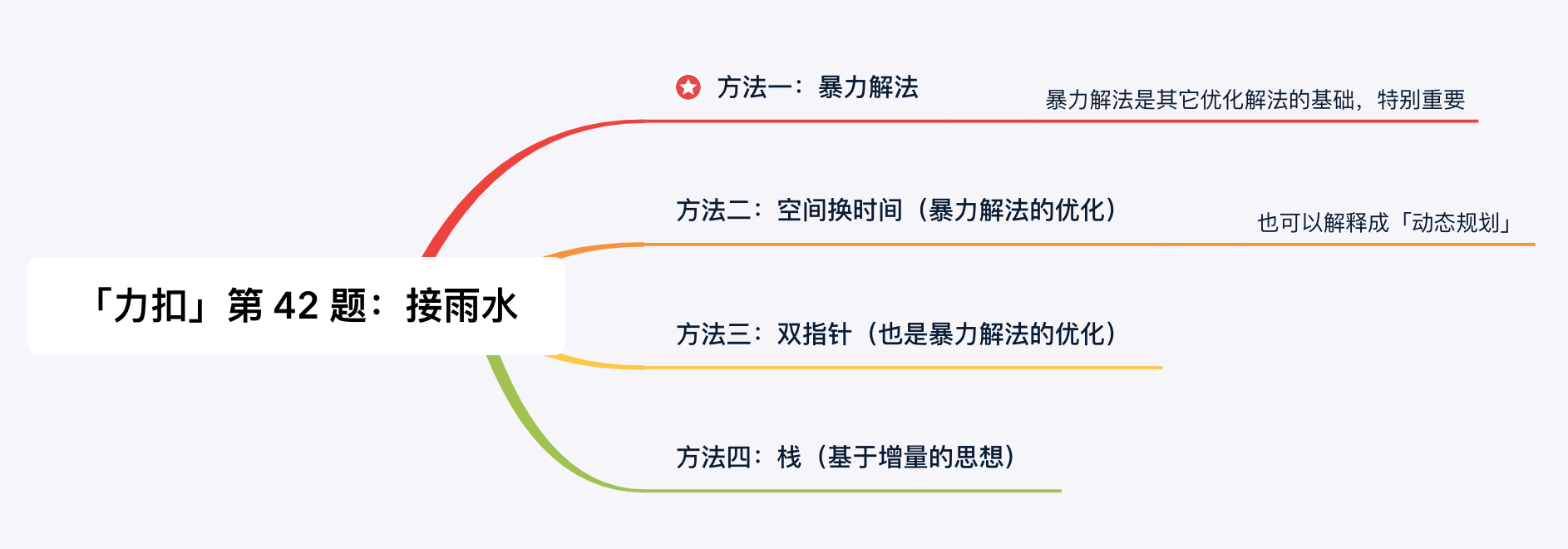
本题我们主要从栈（单调栈）的思想去考虑

我们维护一个单调递减栈 aa，用栈来存储下标（便于计算出积水的长度，从而求出体积），依次遍历一遍 height，当有 height[ i ] 大于栈的顶部元素的值 height[ aa.top() ] 则说明可以形成低洼，即可以积水。

那么此时我们记录并删除栈顶元素 x = aa.top() ，aa.pop() ，通过这时的 i 和新的栈顶元素 aa.top() 可以计算出积水的长度，即 i - aa.top() - 1 。

而高度则通过这时的 height[ i ] 和新的栈顶元素所得的值 height[ aa.top() ] 还有删除的栈顶元素所得的值 height[ x ] 可以计算得出，即 min( height[ i ] , height[ aa.top() ] ) - height[ x ] 。

于是积水的体积等于 长度乘以宽度 。记录并存储下来，如果 height[ i ] 仍大于栈顶元素对应的值，重复进行上述操作。

在对下标 i 处计算能接的雨水量之后，将 i 入栈，继续遍历后面的下标，计算能接的雨水量。遍历结束之后即可得到能接的雨水总量。

我们看一下代码理解

题解代码：

class Solution {
public:
    int trap(vector<int>& height) {
        int sum = 0;
        stack<int> aa;
 
        for(int i = 0;i < height.size();i++){
            while(!aa.empty() && height[i] > height[aa.top()]){
                  int x = aa.top();
                  aa.pop();
 
                  if(aa.empty()){
                      break;
                  }
 
                  int chang = i - aa.top() - 1;
                  int gao = min(height[i],height[aa.top()]) - height[x];
 
                  sum += chang * gao;
            }
 
            aa.push(i);
        }
 
        return sum;
    }
};

复杂性分析

1、时间复杂度：O(n)O(n)。
单次遍历 O(n)O(n) ，每个条形块最多访问两次（由于栈的弹入和弹出），并且弹入和弹出栈都是 O(1)O(1) 的。
2、空间复杂度：O(n)O(n)。 栈最多在阶梯型或平坦型条形块结构中占用 O(n)O(n) 的空间。