- 1Hadoop详解_大数据的特点谁提出的
- 2mfc用oledb链接mysql_MFC用ADO连接数据库(ACCESS)
- 3手动下载并安装nltk_data_nltk data lives in the gh-pages branch of this rep
- 46行代码入门RAG开发_rag代码
- 5matlab的边缘检测方法,Matlab多种图像边缘检测方法
- 6Axure RP 9 for Mac/win:打造极致交互体验的原型设计神器_axure mac
- 7【在FastAPI应用中嵌入Gradio界面的实现方法】如何在有一个Fastapi应用的基础上,新加一个gradio程序_gradio fastapi
- 8打造安全高效的身份管理:七大顶级CIAM工具推荐
- 9基于C++Qt实现考试系统[2024-05-05]_qt考试系统
- 10【ubuntu连接xshell最新2024史上最全小白教程】_ubuntu xshell
力扣动态规划专题(五)子序列问题 不连续子序列与连续子序列 步骤及C++实现
赞
踩

300.最长递增子序列
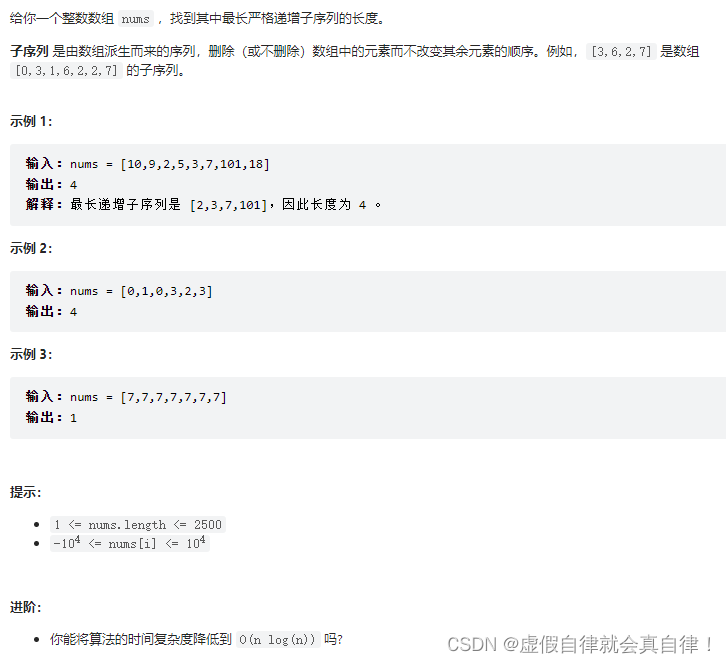
步骤
-
确定dp数组以及下标的含义
dp[i]:i之前(包括i)以nums[i]结尾的最长递增子序列的长度。递增比较时,肯定要比较两个递增子序列的末尾元素,即递增子序列肯定是以末尾元素结尾的,否则比较没有意义 -
确定递推公式
位置i 的最长升序子序列等于 = 位置j 的最长升序子序列 + 1 的最大值,j在[0, i-1]区间。假设dp[i]就是最长的升序子序列,那么dp[j]就是0~i-1的最长升序子序列再+1,即dp[i] = dp[j] + 1,为了取dp[j] + 1的最大值,if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
这里不是要dp[i] 与 dp[j] + 1进行比较,而是要取dp[j] + 1的最大值。 -
dp数组如何初始化
每一个i,对应的最长递增子序列dp[i]起始大小至少都是1 -
确定遍历顺序
dp[i] 是由0到i-1各个位置的最长递增子序列推导而来,那么遍历i一定是从前向后遍历。并且j在[0, i-1]区间,那么j既可以从前到后,也可以从后到前遍历。遍历i在外循环,遍历j在内循环 -
举例推导dp数组
输入:[0,1,0,3,2]

-
C++实现
class Solution { public: int lengthOfLIS(vector<int>& nums) { if(nums.size() <= 1) return nums.size(); vector<int> dp(nums.size(), 1); int result = 0; for(int i=1; i<nums.size(); i++) { for(int j=0; j<i; j++) { if(nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1); } if(dp[i] > result) result = dp[i]; } return result; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
674.最长连续递增子序列
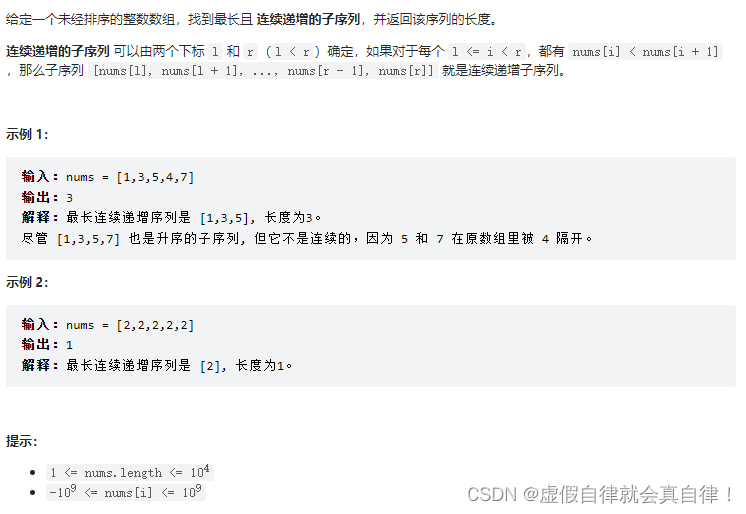
动态规划
步骤
相比于300.最长递增子序列最大的区别在于连续,要求的是最长连续递增序列,体现在递推公式
-
确定dp数组以及下标的含义
dp[i]:以下标i为结尾的连续递增的子序列长度 -
确定递推公式
如果 nums[i] > nums[i - 1],那么以 i 为结尾的连续递增的子序列长度 = 以i - 1为结尾的连续递增的子序列长度 + 1 ,dp[i] = dp[i - 1] + 1;
300题中比较的是nums[i]和nums[j],而j是在[0, i-1]区间的,需要两层for循环。本题则是比较nums[i]和nums[i-1],只需要一层for循环 -
dp数组如何初始化
以下标i为结尾的连续递增的子序列长度最少也应该是1 -
确定遍历顺序
dp[i]依赖dp[i - 1],从前向后遍历 -
举例推导dp数组
输入nums = [1,3,5,4,7]

dp[i]的最大值才是最终结果 -
C++实现
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
if(nums.size() <= 1) return nums.size();
vector<int> dp(nums.size(), 1);
int result = 1;
for(int i=1; i<nums.size(); i++)
{
if(nums[i] > nums[i-1]) dp[i] = dp[i-1] + 1;
if(dp[i] > result) result = dp[i];
}
return result;
}
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
贪心算法
只统计连续的递增序列长度,遇到nums[i] > nums[i-1]就记一次数
class Solution { public: int findLengthOfLCIS(vector<int>& nums) { //贪心算法 if(nums.size() == 0) return 0; int result = 1; int count = 1; for(int i=1; i<nums.size(); i++) { if(nums[i] > nums[i-1]) count++; else count = 1; if(count >result) result = count; } return result; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
718. 最长重复子数组

明确一点,子数组指的是连续子序列。
二维dp数组
步骤
-
确定dp数组以及下标的含义
dp[i][j] :以下标i - 1为结尾的nums1,和以下标j - 1为结尾的nums2,最长重复子数组长度 -
确定递推公式
dp[i][j]的状态只能由dp[i - 1][j - 1]推导出来,当nums1[i - 1] 和nums2[j - 1]相等时,dp[i][j] = dp[i - 1][j - 1] + 1;,因此遍历i 和 j 都要从1开始 -
dp数组如何初始化
虽然dp[i][0] 和dp[0][j]没有意义,但是为了后续递推,dp[i][0] 和dp[0][j]都要初始化为0。例如,如果nums1[0]=nums2[0],那么dp[1][1] = dp[0][0] + 1,只有dp[0][0]初始为0,才能计算dp[1][1],并且符合递推公式。 -
确定遍历顺序
遍历nums1和nums2的先后没有要求,题目要求长度最长的子数组的长度,遍历时要记录dp[i][j]的最大值 -
C++实现
class Solution { public: int findLength(vector<int>& nums1, vector<int>& nums2) { vector<vector<int>> dp(nums1.size()+1, vector<int>(nums2.size()+1, 0)); int result = 0; for(int i=1; i<=nums1.size(); i++) { for(int j=1; j<=nums2.size(); j++) { if(nums1[i-1] == nums2[j-1]) dp[i][j] = dp[i-1][j-1] + 1; if(dp[i][j] > result) result = dp[i][j]; } } return result; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
一维dp数组
二维dp数组中,dp[i][j]都是由dp[i - 1][j - 1]推出的,那么dp[i][j]压缩为一维数组dp[j],也就是dp[j]都是由dp[j - 1]推出的。相当于可以把上一层dp[i - 1][j]拷贝到下一层dp[i][j]来继续用,此时遍历B数组的时候,就要从后向前遍历,这样避免重复覆盖。
class Solution { public: int findLength(vector<int>& nums1, vector<int>& nums2) { //一维dp数组 vector<int> dp(nums2.size()+1, 0); int result = 0; for(int i=1; i<=nums1.size(); i++) { for(int j=nums2.size(); j>0; j--) { if(nums1[i-1] == nums2[j-1]) dp[j] = dp[j-1] + 1; else dp[j] = 0; // 注意这里不相等的时候要有赋0的操作 if(dp[j] > result) result = dp[j]; } } return result; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
1143.最长公共子序列
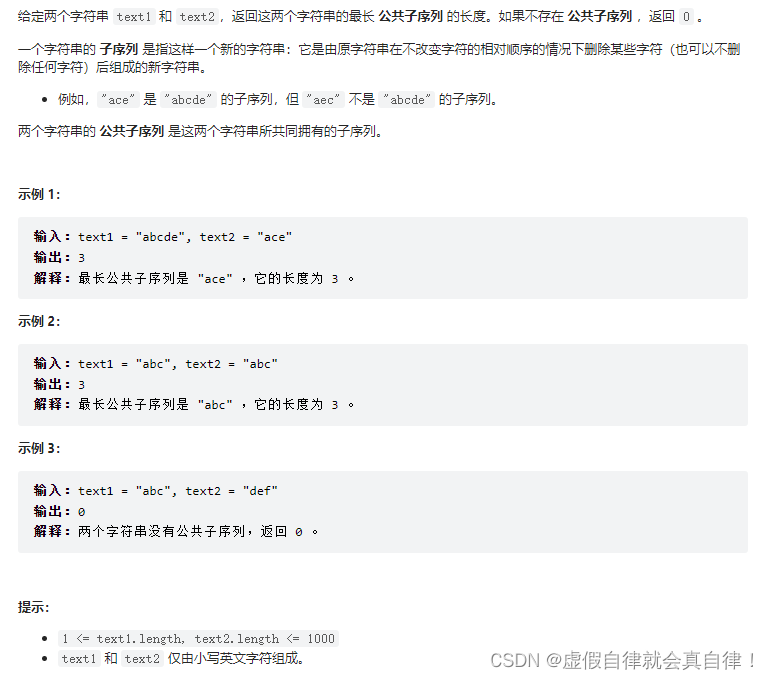
和718题的区别在于不要求连续,但要有相对顺序,例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
步骤
-
确定dp数组以及下标的含义
dp[i][j]:长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列的长度
定义为长度为[0, i]的字符串text1也可以,但是实现比较复杂,需要初始化 -
确定递推公式
- text1[i - 1] 与 text2[j - 1]相同,找到一个公共元素,
dp[i][j] = dp[i - 1][j - 1] + 1; - text1[i - 1] 与 text2[j - 1]不相同,就看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列,取最大的,
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
-
dp数组如何初始化
test1[0, i-1]和空串的最长公共子序列是0,dp[i][0] = 0;,同理dp[0][j]=0。 -
确定遍历顺序
从递推公式来看,有三个方向可以推出dp[i][j],所以要从前向后,从上到下来遍历

-
举例推导dp数组
输入:text1 = “abcde”, text2 = “ace” ,最后红框dp[text1.size()][text2.size()]为最终结果

-
C++实现
class Solution { public: int longestCommonSubsequence(string text1, string text2) { vector<vector<int>> dp(text1.size()+1, vector<int>(text2.size()+1, 0)); //从上到下 从前到后遍历 for(int i=1; i<=text1.size(); i++) { for(int j=1; j<=text2.size(); j++) { if(text1[i-1] == text2[j-1]) dp[i][j] = dp[i-1][j-1] + 1; else dp[i][j] = max(dp[i][j-1], dp[i-1][j]); } } return dp[text1.size()][text2.size()]; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
1035.不相交的线

分析
绘制一些连接两个数字nums1[i] 和nums2[j] 的直线,只要nums1[i] == nums2[j],且直线不能相交。要保证直线不相交,就不能改变数字在原始序列的位置。
换句话说,题目要求的是nums1和nums2的最长公共子序列的长度,这个公共子序列的相对顺序不能改变,也就是题1143。
步骤
-
确定dp数组以及下标的含义
dp[i][j]:长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列的长度
定义为长度为[0, i]的字符串text1也可以,但是实现比较复杂,需要初始化 -
确定递推公式
- text1[i - 1] 与 text2[j - 1]相同,找到一个公共元素,
dp[i][j] = dp[i - 1][j - 1] + 1; - text1[i - 1] 与 text2[j - 1]不相同,就看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列,取最大的,
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
-
dp数组如何初始化
test1[0, i-1]和空串的最长公共子序列是0,dp[i][0] = 0;,同理dp[0][j]=0。 -
确定遍历顺序
从递推公式来看,有三个方向可以推出dp[i][j],所以要从前向后,从上到下来遍历

-
C++实现
class Solution {
public:
int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
vector<vector<int>> dp(nums1.size()+1, vector<int>(nums2.size()+1, 0));
for(int i=1; i<=nums1.size(); i++)
{
for(int j=1; j<=nums2.size(); j++)
{
if(nums1[i-1] == nums2[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
else dp[i][j] = max(dp[i][j-1], dp[i-1][j]);
}
}
return dp[nums1.size()][nums2.size()];
}
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
53. 最大子序和

动态规划
步骤
-
确定dp数组以及下标的含义
dp[i]:包括下标i(以nums[i]为结尾)的最大连续子序列和 -
确定递推公式
dp[i]只有两个方向可以推出来
- nums[i]加入当前连续子序列和,dp[i - 1] + nums[i]
- 从头开始计算当前连续子序列和,nums[i]
取最大的,dp[i] = max(dp[i - 1] + nums[i], nums[i]);
-
dp数组如何初始化
dp[i]依赖于dp[i - 1]的状态,dp[0]是递推公式的基础。根据dp[i]的定义,dp[0] = nums[0] -
确定遍历顺序
dp[i]依赖dp[i - 1],从前向后遍历 -
举例推导dp数组
输入:nums = [-2,1,-3,4,-1,2,1,-5,4],最后的结果不是dp[nums.size() - 1],而是dp[6],和最大的连续子序列。在递推时,可以直接选出最大的dp[i]最为最终结果。

-
C++实现
class Solution { public: int maxSubArray(vector<int>& nums) { vector<int> dp(nums.size(), 0); dp[0] = nums[0];//初始化 从位置1开始遍历 int result = dp[0]; for(int i=1; i<nums.size(); i++) { //dp[i-1]~nums[i]的最长连续子序列 从nums[0]~nums[i]的最长连续子序列 //去两者最大值 dp[i] = max(dp[i-1]+nums[i], nums[i]); if(dp[i] > result) result = dp[i];//筛选出结果 } return result; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
贪心算法
局部最优的情况下,并记录最大的“连续和”,可以推出全局最优。
class Solution {
public:
int maxSubArray(vector<int>& nums) {
//贪心算法
int result = INT32_MIN;//记录最终累计和 全局解
int count = 0;//记录当前累计和 局部最优解
for(int i=1; i<=nums.size(); i++)
{
count += nums[i];//累计求和
if(count > result) result = count;
if(count <= 0) count = 0;//当前累计和小0
}
return result;
}
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15



