- 1【Android Studio】在Mac中更换JDK Location_mac 更换android studio 默认jdk版本
- 2蓝桥杯单片机第五届国赛题目_五届蓝桥杯单片机国赛真题
- 3学习笔记2--自动驾驶汽车的规划与控制_自动驾驶汽车决策与控制pdf
- 4单源最短路径复习--Dijkstra算法和Floyd算法_可以求出某一点到其他所有点的最短路径的是
- 5python中time库引用不正确的_下面关于 time 库引用不正确的是?_学小易找答案
- 6Cannot deserialize value of type `java.time.LocalDate` from Object value
- 7MySQL 8.0 安装部署3个注意事项_mysql8.0+为什么ssl
- 8Linux SSH免密通信 - “ssh-keygen”的基本用法;配置ssh 无需密码即可登录远程服务器
- 9一个快速从中文文本抽取关键短语的工具 ckpe 提取关键短语
- 10linux下安装Adobe Reader(acroread)_linux acroread
自动驾驶决策规划算法第一章_决策规划 老王 总结
赞
踩
前置学习内容: 【自动驾驶】【零基础】基础自动驾驶控制算法笔记
注意:最好学习前置控制算法,因为决策规划仿真中需要用到
感谢:忠厚老实的老王
下面是他的主页:忠厚老实的老王的个人空间_哔哩哔哩_bilibili
目录
序章:决策规划算法概述
第一章:数学基础
第二章:Apollo EM Planner理论篇
第三章:Apollo EM Planner代码篇
终章:决策规划算法总结
序章:决策规划算法概述
自动驾驶6个级别:L0-L5
| L0 | 没有任何自动驾驶功能 |
| L1 | 有横向和纵向的自动驾驶功能,但是横纵向无法联合使用 |
| L2 | 横纵向可以联合使用,但驾驶员必须对一切状况负责 |
| L3 | 功能与L2基本相同,最大的区别在于责任,对于部分场景,驾驶员不必负责 |
| L4 | 大部分道路皆可自动驾驶,大部分场景都不需要驾驶员负责 |
| L5 | 完全自动驾驶 |
两条关键因素区分:功能和责任
L0-L2主要是功能区分,L3-L5主要是责任区分,而不同公司L2与L2之间差距巨大,只要厂家宣称驾驶员需要负全责,即使功能做到了L2,本质上还是L2
L2本身比较宽泛,只有定速巡航+车道保持的汽车也是L2,什么都能做,但是驾驶员要负全责的汽车也是L2
决策规划算法就是普通L2到什么都能做的L2的一个重要模块
| 感知 | 人的眼睛,耳朵 |
| 控制 | 人的小脑,双脚 |
| 决策规划 | 人的大脑 |
功能越往上做,越丰富,越复杂,决策规划算法越重要,也越难在L4中决策规划模块可以说是最重要,也是最复杂,最难做的模块
难做到把整个模块一分为三,还要加上地图模块,每块单独地去做才能勉强完成“大脑”的工作,而且截止到2021年也不能说完全的解决
整个决策规划模块一分为三,下面分别介绍
1、导航规划算法,此算法将计算出大地图上A到B的最优路径,此算法与机器人导航,手机导航算法基本一致,长度在几公里到几百公里不等,该算法是整个规划模块中最为成熟的算法
特点:导航算法会给一个粗略的,大范围的路径,但是此路径不会考虑如何避障,也不会考虑车辆动力学约束,一般规划的路径时不规则的折线。导航算法一般只需要执行一次,只有遇到大范围的拥堵,施工,偏航等情况才会再次执行
2、行为规划算法,又叫决策算法,决定车辆行驶意图的算法 ,对于静态障碍物,到底往左绕还是往右绕,对于动态障碍物,到底该减速避让,还是加速超车?决策算法决定了车辆的意图,这也是整个规划算法中最难做的部分。
特点:决策算法会给一个车辆的行驶意图,会指导车辆该避让,该超车,该往左转该右转,但是决策不会给具体的运动建议,例如往左转多少度,车辆加速到多少。
实际环境瞬息万变,因此决策算法需要较高的执行频率,一般为10Hz
决策算法需要有一定的稳定性,不允许在周围环境稳定时出现“朝令夕改”现象
3、运动规划算法:根据决策给出的行为意图在相关的时空中搜索出(或优化出)一条具有详细路径速度信息,并且满足各个约束条件的轨迹,并将此轨迹发给控制模块去跟踪,此轨迹长度一般在几米到几十米不等
特点:运功规划生成的轨迹是决策规划模块的最终输出,具有详细的路径速度的信息,执行频率与决策相同,为10Hz,同样,运动规划也要求具有一定的稳定性。
本次教学将详细讲解决策规划算法与运动规划算法,不讲当行算法(因为相对成熟),以Apollo EM planner为例,EM planner是Apollo的经典决策规划算法,擅长处理复杂环境下的决策规划问题,也是Apollo默认的决策规划算法。
提醒:截止到2021年,Apollo已经迭代到6.0,EM planner在Apollo 1.5中加入,目前6.0的EM planner与1.5相比已经发生了一些变化,现在6.0的EM planner换了个名字叫做OnLane Planning,我现在讲解的是最初的1.5版本的EM planner,当然思想上殊途同归,不过建议学完后看一看6.0的OnLane Planning
第一章:数学基础
一、细说五次多项式
五次多项式时规划论文里的常客,本节将详细解释五次多项式的特殊性
tips:本节难度较大,但并不重要,听不懂记住结论即可
1、Jerk介绍
车辆运动规划中,一个非常重要的指标就是舒适性,在物理中,衡量舒适性的物理量是跃度,英语为Jerk
Jerk的定义为加速度的导数,即(a为加速度),Jerk的绝对值越小,意味着a的变化越平缓,a的变化越平缓也就意味着越舒适
设有一个质点的轨迹s=f(t),则 ,若在[0,T]区间的时间中,Jerk的绝对值都比较小,那就意味着在[0,T]内规划的轨迹是比较舒适的
那么数学问题就变成了:若有一个函数s = f(t),那么什么样的f(t)使得在[0,T]内Jerk的绝对值变化平缓?由于绝对值处理较繁,一般改成平方,也就是说,问题变为
显然,积分是一个关于f(t)的泛函,积分的值取决于f(t)在[0,T]上的整体形状
那么取极小值的f(t)是什么?显然,当f(t)为二次或者二次以下函数时,
最小
所以若要让Jerk在[0,T]上的绝对值最小,f(t)应取二次或者二次以下函数
但是真实情况远比想象中复杂,因为真实的s = f(t)往往带有约束
6个边界条件

二次函数只有3个系数(a,b,c),无法满足6个边界条件
在真实情况下,往往要求带边界约束的泛函
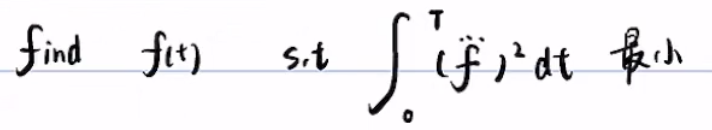
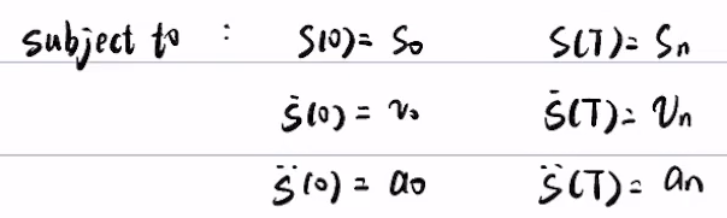
那么满足带约束的泛函极值问题的解是什么?
答案:五次多项式
解:显然f(t)只可能是在[0,T]上是有界连续函数,因为无论是无界还是有界间断函数都会使Jerk出现无穷大
所以不妨设
![]()
带入边界条件
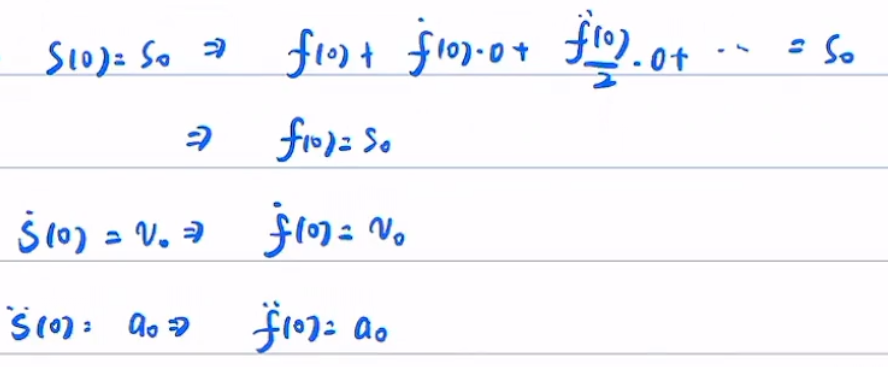
最终得到
![]()
观察这个式子,由于,所以
的值不影响Jerk
其次边界条件

记![]()
则有
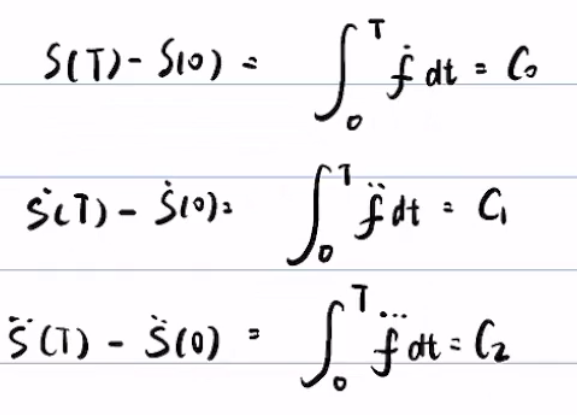
最终,问题变为求 下的极小值
下的极小值
泛函极值的必要条件为Euler-Lagrange方程
复习:使泛函![]() 取极小值的f,满足E-L方程
取极小值的f,满足E-L方程
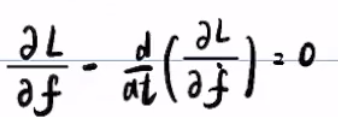
求解:泛函
约束: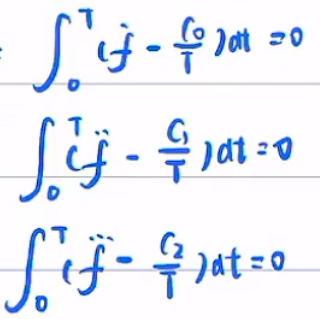
Lagrange乘子
![]()
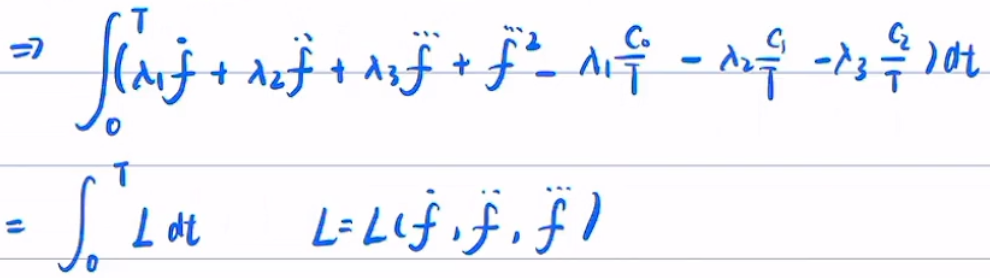
广义E-L方程:
分别求偏导得到
![]()
带入

结论:五次多项式是带约束的泛函取极小值的解函数
所以五次多项式在规划中才这么常见
二、凸优化与非凸优化
自动驾驶规划目标:算出一条满足约束的最优轨迹
然而,什么是“最优”?
指标:①平滑性;②舒适性;③尽可能短,耗时少。
约束:①轨迹连续性;②无碰撞;③遵守交规;④车辆动力学。
衡量轨迹质量用Cost function表示
假设(系数均为未知常数)
则Cost Function
J越小,意味着越平滑舒适,当然也要满足各种约束
数学问题:求解Cost Function在约束条件下的最小值问题
如何计算y=f(x)的最小值(在约束下)
回忆:高中时如何解y = f(x)在x∈[a,b]上的最小值(f(x)是连续可导函数)
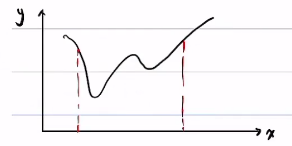
①算出
②求出y' = f'(x)
③令y' = 0,解出f'(x)= 0的根,设为
④计算与
比较,
中最小的那个就是y = f(x)在[a,b]上的最小值
但是此方法无法快速求解高维度复杂约束下的最小值问题,比如
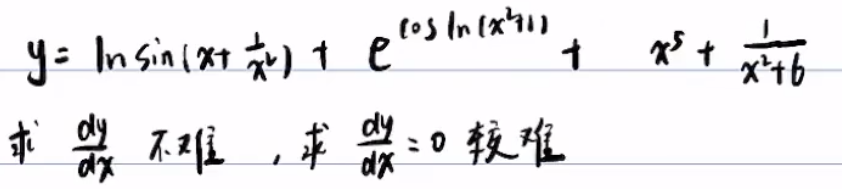
有的时候就算求出极值点,但是极值点很多,难以快速计算,或者约束复杂

一般求复杂函数在复杂约束下的最小值问题都采用迭代法
常见迭代法有
1、牛顿法《数值分析》
2、梯度下降法
3、高斯牛顿法《视觉slam十四讲》
梯度下降法大概过程

按照梯度的反向来迭代,通过导数大小来判断收敛,要么收敛到极值点,要么收敛到边界
迭代法缺点:对初值敏感,有可能会收敛到局部极小值
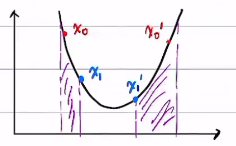

也有一些性质较好的问题,比如:

或者

这种性质比较好的问题叫做凸优化
凸优化必有两个性质:
①Cost function只有一个极值点,且为极小值(凸函数)
②约束空间是一块“完整的”“不破碎的”空间(凸空间)
求凸函数在凸空间的最小值问题称为凸优化
凸空间的严谨定义,由如多边形引申
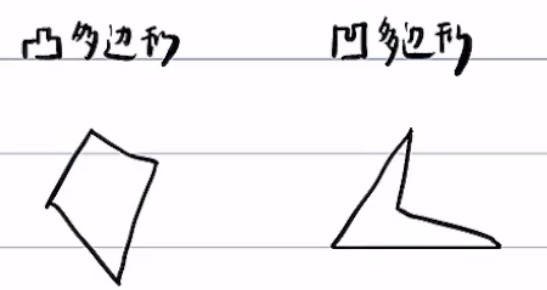
凸多边形定义:对于多边形内部任意的点x,y,都有(x+y)/2也在多边形内部,此多边形为凸多边形
凹多边形定义:对于多边形内部存在点x,y,使得(x+y)/2不在多边形内部,此多边形为凹多边形
凸空间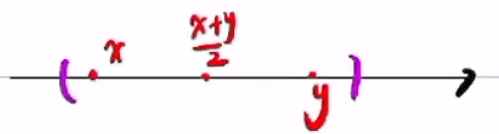
非凸空间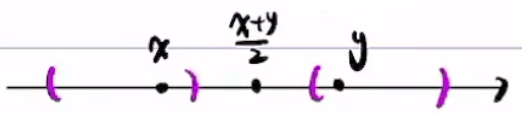
凸优化是最简单的唯一研究明白的非线性优化方法,是所有优化问题的基石
自动驾驶规划的Cost function是凸的,约束空间也得是凸空间才可以当作凸优化问题求解
问题:自动驾驶避障约束空间是不是凸空间 答案:不是
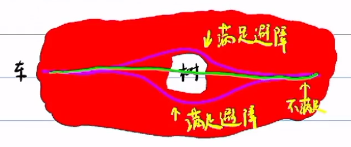
如图,上面的线和下面都满足避障约束,但是加起来除以二就不满足了,因此不是凸空间,是一个“破碎的空间”
对于动态的障碍物也是一样的
假设场景为一个人和一辆车,车要动态避障行人

规划车速快或者慢,都满足避障约束


但是如果取二分之车速,就不满足约束,会发生交通事故

静态和动态避障约束空间都不是凸的,所以规划问题是比较难的
如何求解非凸问题的最小值?
答:目前为止,并无完美的非凸问题算法,求解非凸问题的主要思路是找非凸问题中的凸结构
启发式算法:先随机在约束空间采样一些离散的函数值,比大小,取最小的作为迭代初值
举例:在这些黄色采样点中找到最小点作为初值迭代
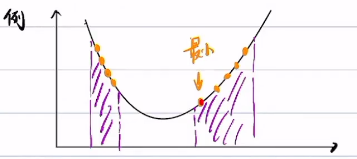
对于非凸函数或者非凸空间,也是一样,先在约束空间采样,找到采样点的最小值,本质上是连续空间离散化后,离散约束空间的最优解
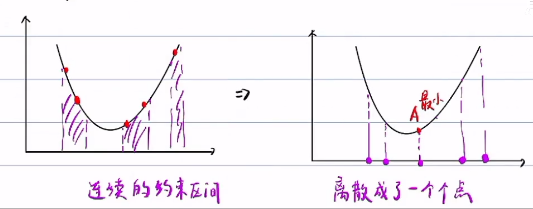
采样,比大小,求出A最小,A本质上是离散约束空间的最优解(粗解)
非凸空间 --> 离散化 --> 粗解 --> 迭代 --> 最终解
对于一个非凸问题,如果采样越少,越容易收敛到局部最优,而不是全局最优
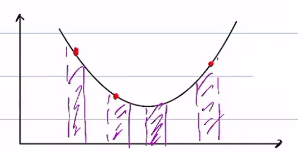
那么我采样点多一些,就会出现“维度灾难”
一维要采样100个点,二维要采样100*100 = 1w个点,三维可能要100w个点
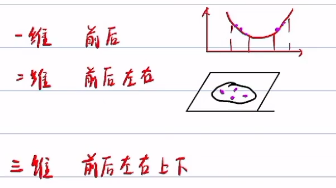
所以非凸问题没有一个尽善尽美的解法,只能根据实际问题去调整
三、直角坐标与自然坐标转换
本节主要推导Frenet坐标系与Cartesian坐标转换
龙格现象:高次多项式拟合可能会出现震荡,慎用高次多项式

尽可能使用分段低次多项式去拟合,而不是高次多项式
自然坐标与直角坐标转换的难度巨大,需要对微积分非常熟练,熟悉曲线坐标系
幸运的是,不需要理解推导过程,只需要记住结论
给出两种方案:
①参考博客,实在看不懂记住结论
Frenet坐标系与Cartesian坐标系互转(一):公式推导_windSeS的博客-CSDN博客_frenet坐标系②和老王一起推导,难度稍低
老王自创的向量法,可以降低推导难度
1、准备工作以及辅助公式推导
下面开始推导的准备工作
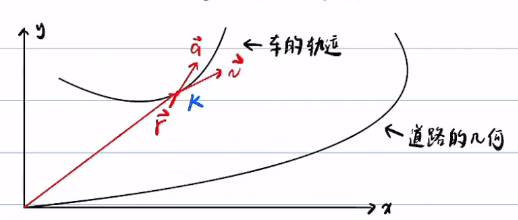
车记为host vehicle
已知车在Cartesian坐标系下的,求车在以道路为坐标轴的frenet坐标下的坐标
,其中
frenet坐标系与Cartesian坐标系定义如下

对于 EM planner,求
对于lattice planner,求
可以互相转化
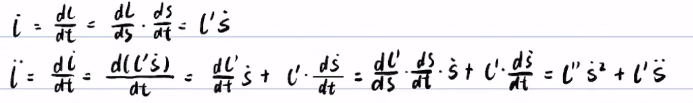
EM planner采用
在推导中,难度最大的就是曲线坐标系
曲线坐标系与直角坐标系的两点不同:
①曲线坐标系的基向量一般不是常向量

②点的曲线坐标变换与点的实际位移一般不一致
在直角坐标系下只有一个dx,在自然坐标系下有不同的ds
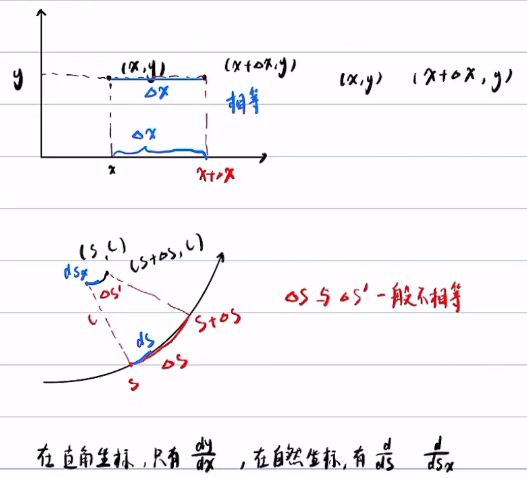
比如,车的轨迹在道路上的投影,两个速度一般不相等的

预备知识1:

拓展:
预备知识2: frenet公式
在曲线坐标系中,一般不为
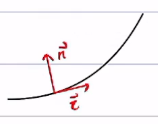
frenet公式:
其中:k为曲率

拓展:

,
,ds指的是坐标轴的ds,上面四个公式的k都是直角坐标系下的k
拓展2:
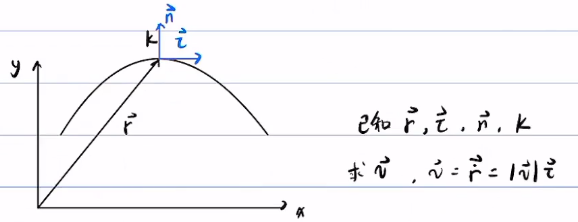
求

总结:
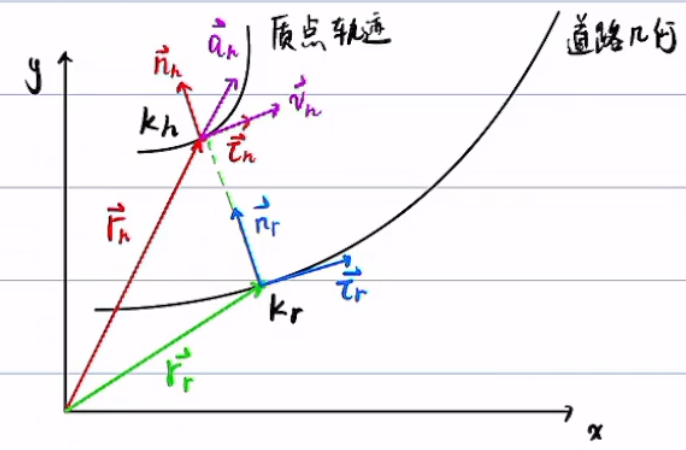
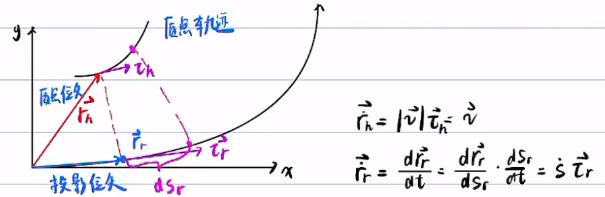
以下变量都以Cartesian坐标为准
| 车的位矢 | 投影位矢 | ||
| 车的速度 | 车在道路上的投影的速率 | ||
| 车的加速度 | 投影位矢在道路几何上的曲率 | ||
| 车的位矢在车轨迹上的曲率 | 投影位矢在道路几何上的切向方向单位向量 | ||
| 车的位矢在车轨迹上的切线方向单位向量 | 投影位矢在道路几何上的法向方向单位向量 | ||
| 车的位矢在车轨迹上的法线方向单位向量 |
辅助公式
要解这个问题我们分三步:
第一步:7个辅助公式
第二步:找到车在frenet坐标下的投影点在Cartesian的坐标,记为

计算投影位矢以及其切向法向单位向量![]()
第三步:利用向量三角形,以及微积分求出
核心公式:
如何找到在frenet坐标下的投影
暂时先不管,假设已经找到了
自然可得到
下面开始正式计算:
(1)计算
核心公式,把
挪到等式右边得到
,
然后两边点乘得到:
注意:这里\overrightarrow{n_r} \cdot \overrightarrow{n_r} = 1,\overrightarrow{\n_r} \cdot \overrightarrow{\tau_r} = 0
(2)计算
对核心公式两边求导得到:
利用辅助公式①②⑤⑥带入![]()
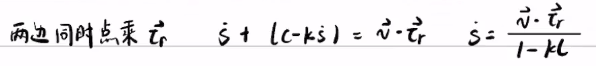
和博客有所不同,但其实一样

(3)计算
由(2)得到![]() ,两边同时点乘
,两边同时点乘
立刻得到![]()
(4)计算
利用上面计算的与
计算得到
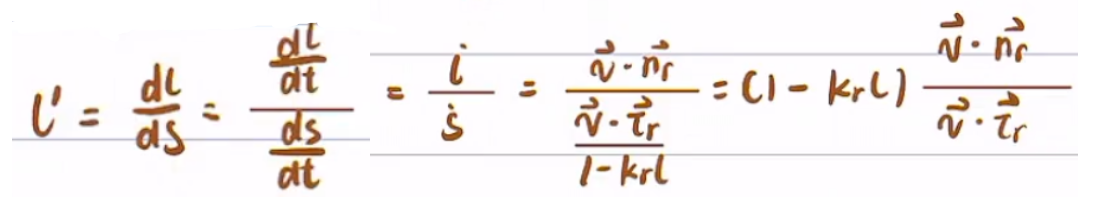
(ds为frenet坐标轴的弧坐标的导数,所以ds/dt = )
(5)计算
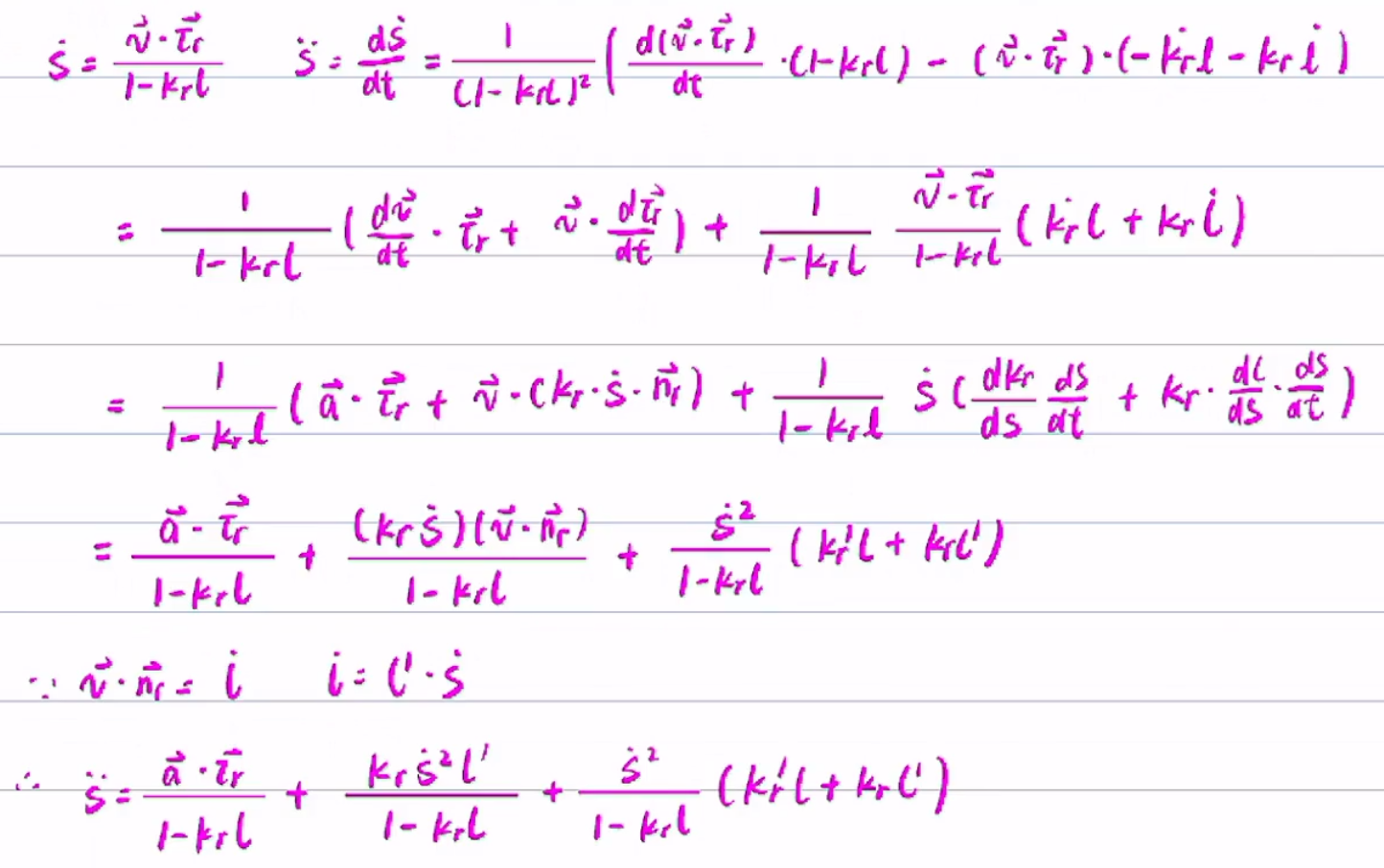
博客公式推导:
辅助公式⑦ ![]()

(6)计算

(7)计算
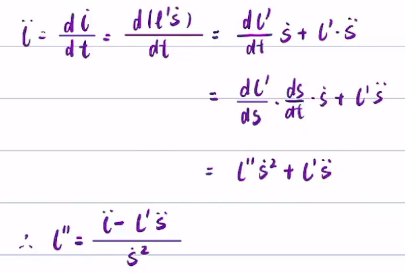
最终得到7个公式,可以把直角坐标系转换为自然坐标系
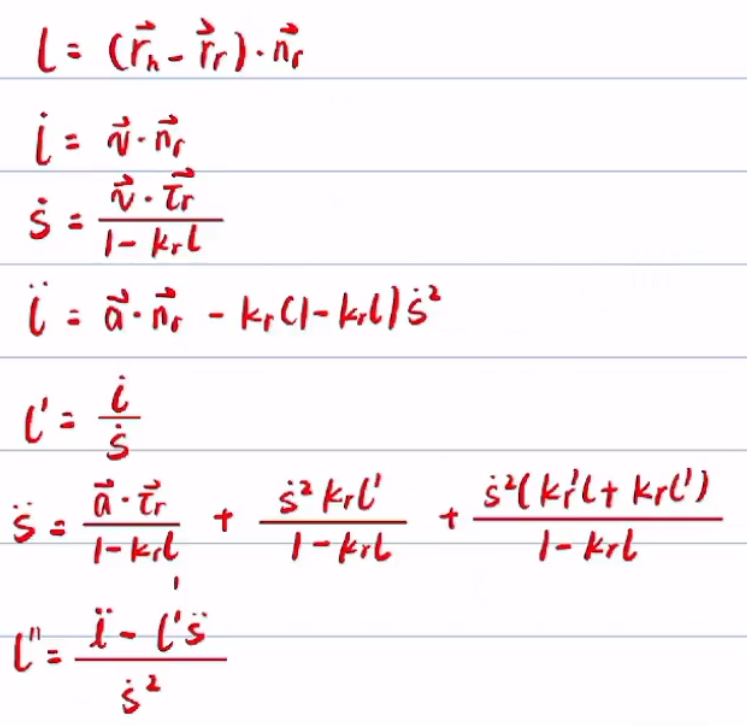
遗留的三个问题
1、如何找到
2、如何计算 s
3、如何从转回到直角坐标系去
3、匹配点
如何找到在《自动驾驶控制算法第七讲》有讲过
一般reference line都是离散点,只讲离散点的
假设曲线上有一系列离散点,如果有蓝线的表达式,可以得到理想投影,
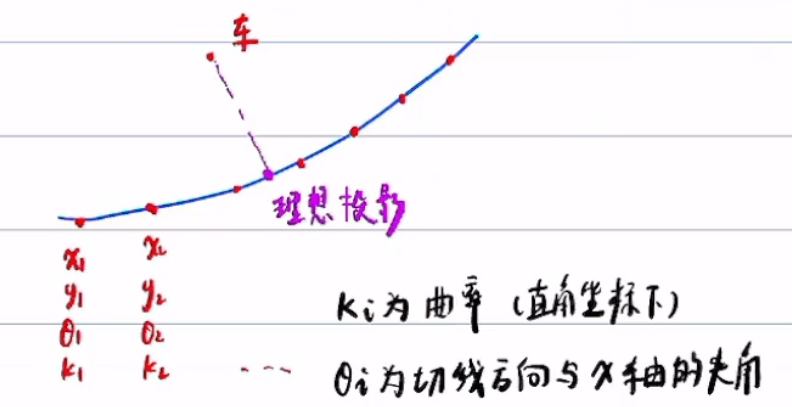
然而一般没有蓝线,只有离散点,以及他们的,在离散曲线下的投影,必然是一个近似解,不可能得到一个理想投影。因为离散曲线缺失信息。只要近似程度满足自动驾驶要求即可。
找到匹配点可以进行近似
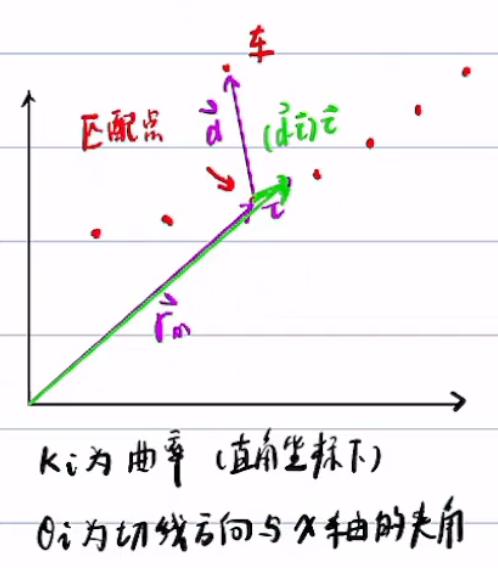
找到距离最短的,此点成为匹配点

原理
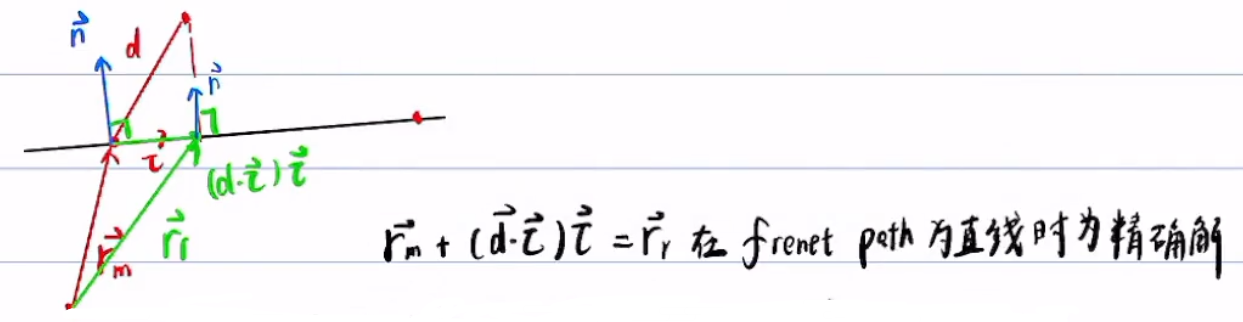
若为弧线,当曲率不太大,且离散的点较密时,精度也较高

求

下面看如何计算s:以直线代替弧长
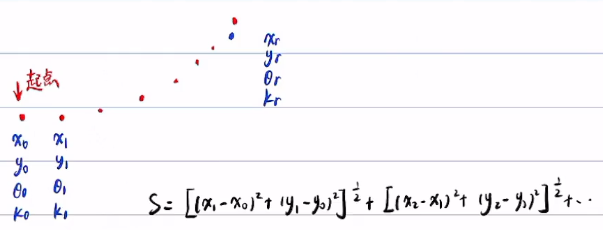
当路径点足够密,误差可以忽略
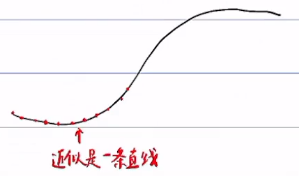
有其他更精确的算法,但是不稳定,以分段直线近似曲线虽然比较糙,但是对参数变化不敏感(robust)
精确算法例子:

虽然算法比较糙,但是计算的快,而且鲁棒,大多数场景适用
下面看如何从自然坐标转换到直角坐标,即
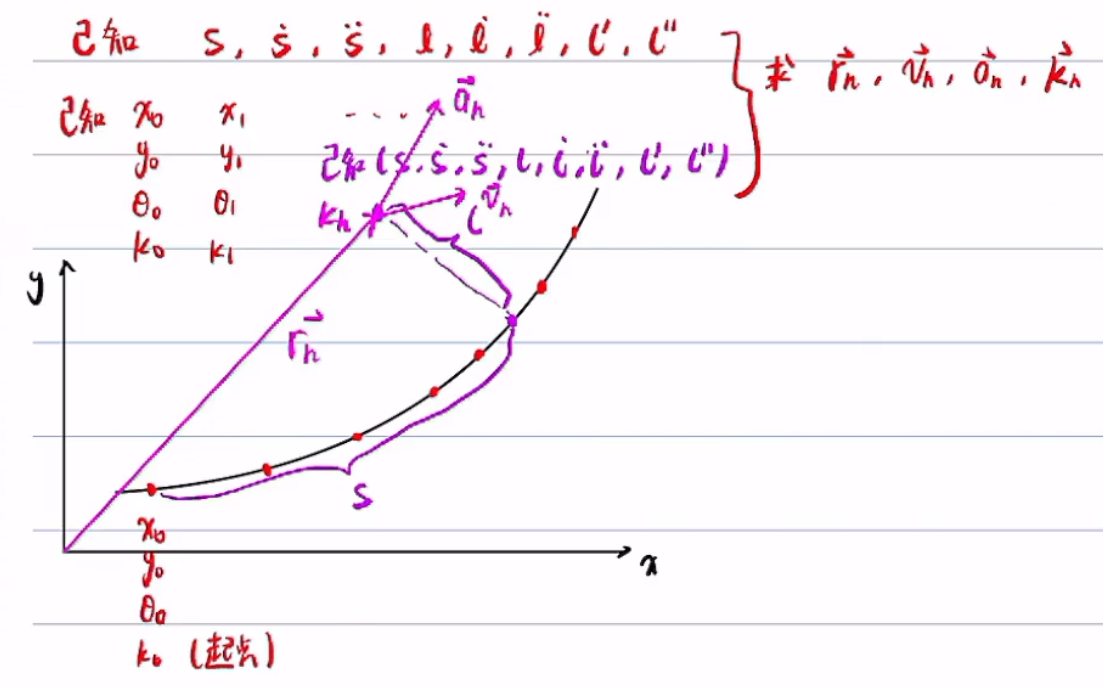
4、Frenet坐标转Cattisian坐标
关键还是找投影点的
1、计算 的对应表,即每个frenet坐标轴上的离散点的
与
的对应关系
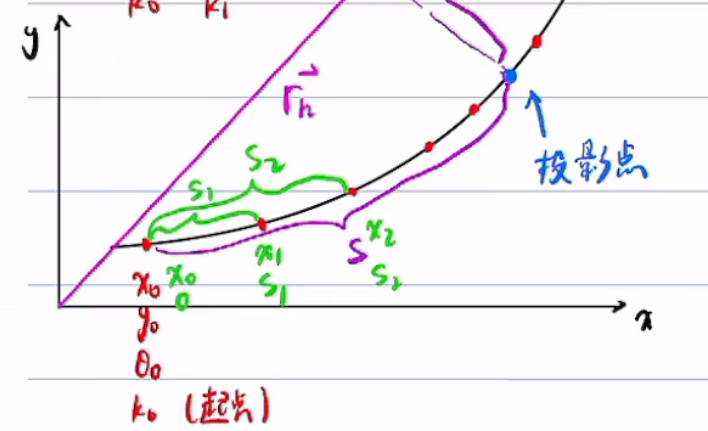
得到

2、查找 表,找到
使得
,
与
对应的
记为
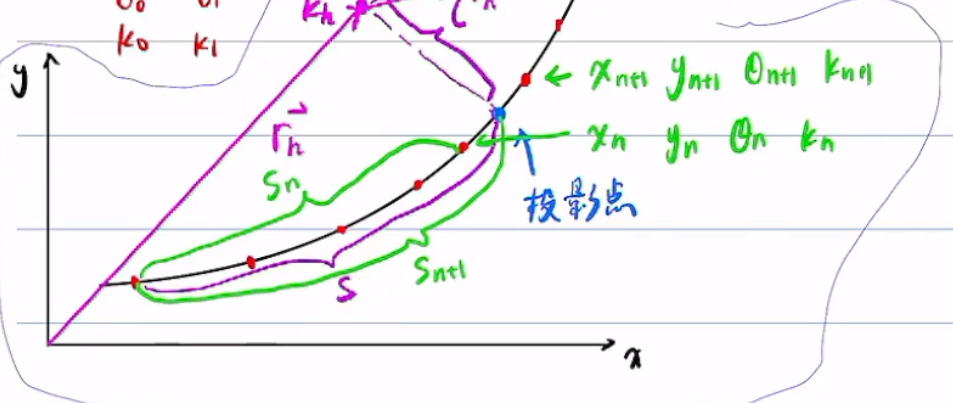
找到以及
x_{n+1},y_{n+1},\theta_{n+1},k_{n+1}
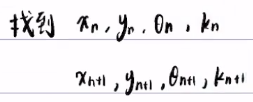
3、其余变量使用公式算出
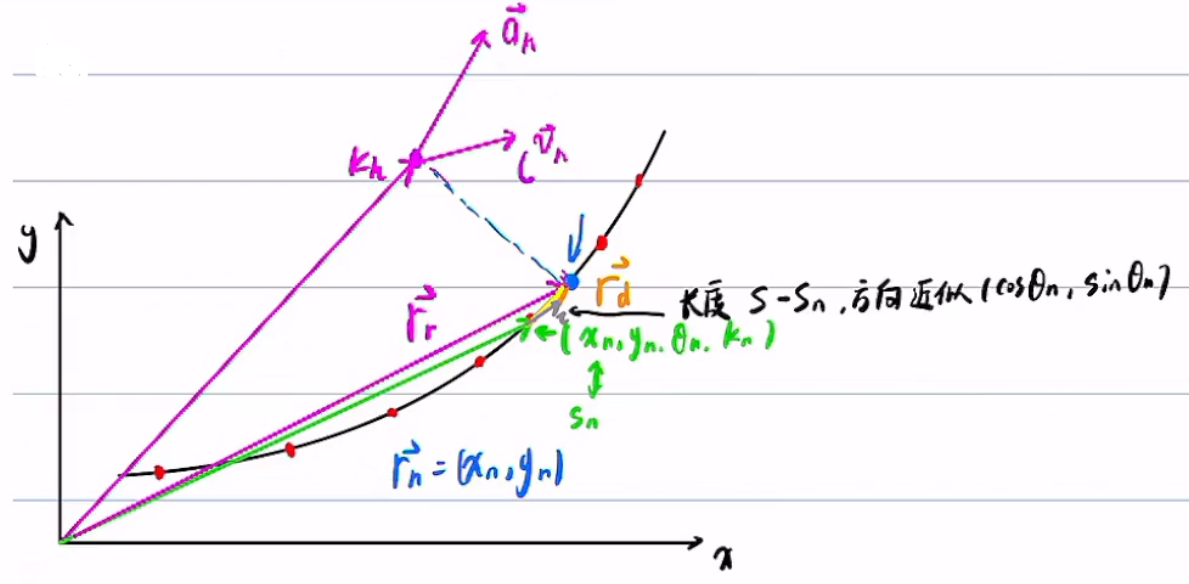
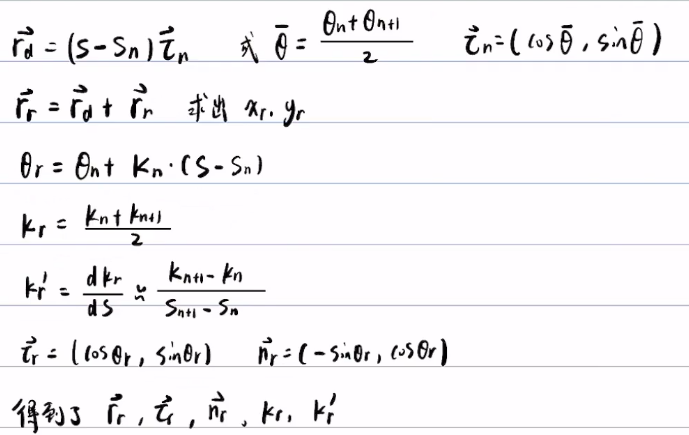
4、至此,我们就可以从自然坐标转换到直角坐标
下面进行推导:
已知,求
首先这里给出上面推导过的直角坐标转换自然坐标公式:
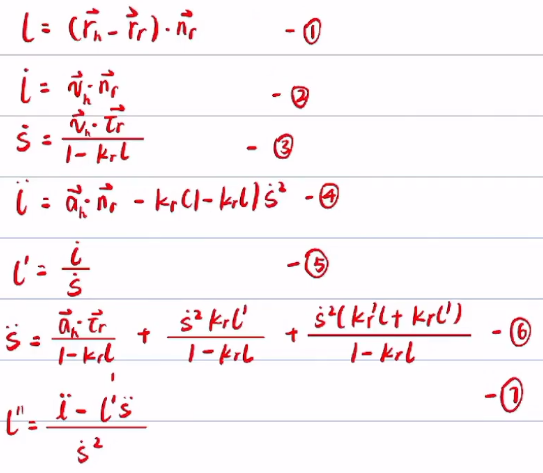
接下来计算
(1)算
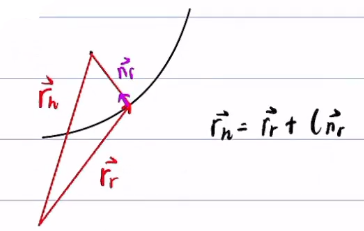
根据几何关系可以得到
(2)算
由公式②③
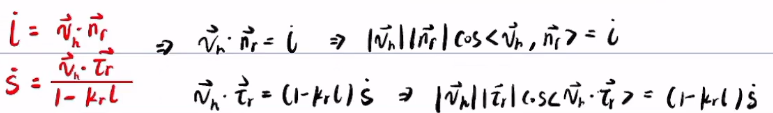
设与x轴夹角为

带入得到v的模

接下来算方向,吧上面两个式子相除得到,(注意这里结合公式⑤计算l')
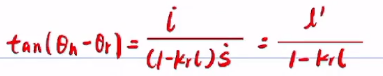
得到![]()
由此计算出方向向量
![]()
(3)算
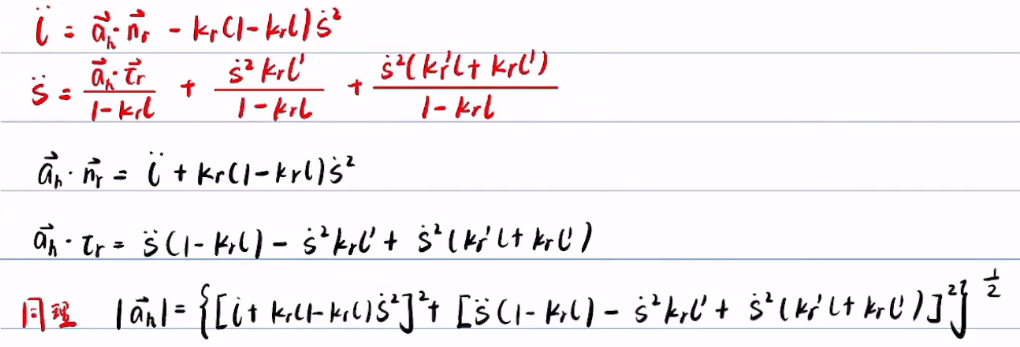
和上面差不多

注意,博客中的,实际上是
。博客中的
,实际上是
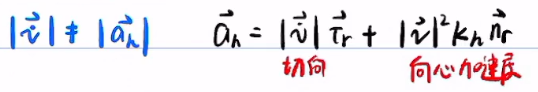

(4)算
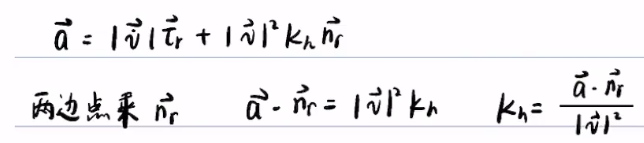
至此,已经介绍完第一章
第二章如下
自动驾驶决策规划算法第二章_免费教学录影带的博客-CSDN博客