LLM大模型学习圣经：从0到1吃透Transformer技术底座_技术自由圈 尼恩

尼恩：LLM大模型学习圣经PDF的起源

在40岁老架构师 尼恩的读者交流群(50+)中，经常性的指导小伙伴们改造简历。

经过尼恩的改造之后，很多小伙伴拿到了一线互联网企业如得物、阿里、滴滴、极兔、有赞、希音、百度、网易、美团的面试机会，拿到了大厂机会。

然而，其中一个成功案例，是一个9年经验 网易的小伙伴，拿到了一个年薪近80W的大模型架构offer，逆涨50%，那是在去年2023年的 5月。

• 惊天大逆袭：8年小伙20天时间提75W年薪offer，逆涨50%，秘诀在这

不到1年，小伙伴也在团队站稳了脚跟，成为了名副其实的大模型架构师。

目前，他管理了10人左右的团队，包括一个2-3人的python算法小分队，包括一个3-4人Java应用开发小分队，包括一个2-3人实施运维小分队。并且他们的产品也收到了丰厚的经济回报， 他们的AIGC大模型产品，好像已经实施了不下10家的大中型企业客户。

当然，尼恩更关注的，主要还是他的个人的职业身价。

小伙伴反馈，不到一年，他现在是人才市场的香馍馍。怎么说呢？他现在职业机会，不知道有多少, 让现在一个机会没有的小伙伴们羡慕不已。

只要他在BOSS上把简历一打开， 就有大量的猎头、甲方公司挖他，机会可以说是非常非常非常多，给他抛绣球的不知道有多少：

并且来找他的，很多都是按照P8标准，年薪200W来的。

相当于他不到1年时间， 职业身价翻了1倍多，可以拿到年薪 200W的offer了。

回想一下，去年小伙伴来找尼恩的时候， 可谓是 令人唏嘘。

当时，小伙伴被网易裁员， 自己折腾 2个月，没什么好的offer， 才找尼恩求助。

当时，小伙伴其实并没有做过的大模型架构， 仅仅具备一些 通用架构（ JAVA 架构、K8S云原生架构） 能力，而且这些能力还没有完全成型。 特别说明，他当时 没有做过大模型的架构，对大模型架构是一片空白。

尼恩在指导他做通用架构（ JAVA 架构、K8S云原生架构）, 当时候也是 壮着胆子， 死马当作活马，指导他改造为 大模型架构师。

回忆起当时决策的出发点，主要有两个：

（1）架构思想和体系，本身和语言无关，和业务也关系不大，都是通的。

（2）小伙伴本身也熟悉一点点深度学习，懂python，懂点深度学习的框架，至少，demo能跑起来。

（3）大模型面试稀缺，反正面试官也不是太懂。

基于这个3个，尼恩大胆的决策，指导他往大模型架构走，先改造简历，然后去面试大模型的工程架构师，特别注意，这个小伙伴面的不是大模型算法架构师。

没想到，由于尼恩的大胆指导， 小伙伴成了。

没想到，由于尼恩的大胆指导， 小伙伴成了， 而且是大成，实现了真正的逆天改命。

既然有一个这么成功的案例，尼恩能想到的，就是希望能帮助更多的社群小伙伴， 成长为大模型架构师，也去逆天改命。

于是，从2024年的4月份开始，尼恩开始写 《LLM大模型学习圣经》，帮助大家穿透大模型，走向大模型之路。

《LLM大模型学习圣经》应该是一个很大的系列，包括本文 《LLM大模型学习圣经：从0到1吃透Transformer技术底座》，这个是一个基础理论篇。另外好戏刚刚开始， 后面会有实战篇，架构篇等等出来。

在尼恩的架构师哲学中，开宗明义：架构和语言无关，架构的思想和模式，本就是想通的。

架构思想和体系，本身和语言无关，和业务也关系不大，都是通的。

所以，尼恩用自己的架构内功，以及20年时间积累的架构洪荒之力，通过《LLM大模型学习圣经》，给大家做一下系统化、体系化的LLM梳理，使得大家内力猛增，成为大模型架构师，然后实现”offer直提”， 逆天改命。

尼恩 《LLM大模型学习圣经》PDF 系列文档，会延续尼恩的一贯风格，会持续迭代，持续升级。

这个文档将成为大家 学习大模型的杀手锏， 此文当最新PDF版本，可以来《技术自由圈》公号获取。

大模型定义

大语言模型（英文：Large Language Model，缩写LLM），即大型语言模型 (LLM)，

大型语言模型 (LLM) 之所以大，是指 具有大规模参数和复杂计算结构（超过 10 亿个参数），LLM通常基于 Transformer 模型架构，由深度神经网络构建，对海量数据进行预训练处理。

LLM的特点是规模庞大，包含数十亿的参数，帮助它们学习语言数据中的复杂模式。大模型的底层转换器包含一系列神经网络，分为编码器和解码器，且具有自注意力功能。

下面是来自 维基百科的 解释：

一个大型语言模型（LLM）以其实现通用语言理解和生成的能力而引人注目。LLM通过在计算密集的自监督和半监督训练过程中从文本文档中学习统计关系来获得这些能力。LLM是遵循Transformer架构的人工神经网络。

简单来说，两个特点：

（1） LLM模型基本上是一个具有大量参数/海量参数的神经网络。

模型的大小即参数数量。 模型越大，参数越多。

例如，GPT-3有1750亿个参数，而GPT-4可能有超过1万亿个参数。

（2）LLM是在大量文本数据集（如书籍、网站或用户生成内容）上进行训练的。

大型语言模型 (LLM) 是一种在海量文本数据上进行训练的深度学习模型，用于学习语言的模式、语法、语义和语境。

LLM旨在理解和生成新的内容，LLM以自然的方式，按照提示，生成新文本或者其他形式的内容。

ChatGPT这类的预训练模型在训练过程中需使用的数据样本较多。ChatGPT接受了从互联网上抓取的数千亿个分词的训练，而庞大的训练数据集包含有害言论，会被人工智能学习。

对于ChatGPT这样的语言模型，如果没有人工标注来筛除一些不恰当的内容，那么它不仅会给出一些错误的信息，更会对用户造成心理不适。这就需要数据的标注。

由于样本数非常多，数据标注的需求较高。数据标注的工作流程包括数据标注、打标签、分类、调整和处理等，是构建AI模型的数据准备和预处理工作中不可或缺的一环。

大模型的表现形式

对很多大模型小白来说，一个直观的问题是：大模型的表现形式，是什么？

是一个可以执行的程序？

是一个数据库？

实际上， 一个训练好的大模型，是一个 特定格式的文件。

比如，Meta 开发并“开放”的LLaMA-2大模型，是其此前发布的大模型LLaMA的升级迭代版本，是一个巨大进步的版本。
LLaMA-2是一个基础模型，Meta开放了两个版本，一个是纯无监督训练出来的基础模型，另一个是在基础模型之上进行有监督微调SFT和人类反馈的强化学习RLHF进行训练的Chat模型。

所发布的SFT、RLHF两个版本中，都提供了7B、13B 和70B的三个参数规模的模型。

LLaMA-2-70B大模型，表现形式就是下面的一个文件

Llama 原始的意思是“美洲驼【A llama is a South American animal with thick hair, which looks like a small camel without a hump.】”，也因此，许多基于 LLaMA的模型都以动物名称来命名。

在上面的图像中，parameters 文件是 Meta’s Llama-2-70b model，其大小为140GB，包含70亿个参数（以数字格式表示）。run.c 文件是推理程序，使用这些参数进行模型推理。

这是huggingface设计的一种新格式，大致就是以更加紧凑、跨框架的方式存储Dict[str, Tensor]，主要存储的内容为tensor的名字（字符串）及内容（权重）。

其官网对文件格式的详细内容进行了解释，本质上就是一个JSON文件加上若干binary形式的buffer。

对于tensor而言，它只存储了数据类型、形状、对应的数据区域起点和终点。

因此它只支持存储dense and contiguous tensor，也就是稠密张量（没有stride，没有view等信息）。

本质上，它就像存储了一大块连续的内存，甚至可以直接把文件映射到内存里（使用Python的mmap模块）。

.safetensors支持五种框架，包括pytorch、TensorFlow、flax（jax）、paddle（paddlepaddle）、numpy。

对每个框架都提供了save/save_file/load/load_file这四个函数：

• load( data: bytes, device = ‘cpu’ ) → Dict[str, Tensor]
• load_file( filename: Union[str, os.PathLike], device = ‘cpu’ ) → Dict[str, Tensor]
• save( tensors: Dict[str, Tensor], metadata: Optional = None ) → bytes
• save_file( tensors: Dict, filename: Union[str, os.PathLike], metadata: Optional = None ) → None

对于numpy，函数没有device参数；Tensor类型根据具体的框架替换成框架的具体类，例如torch.Tensor或者np.array。

训练这些超大型模型非常昂贵。像GPT-3这样的模型的训练成本高达数百万美元。

截至今日，最杰出的模型GPT-4不再是单一模型，而是由多个模型混合而成。每个模型都是在特定领域进行训练或微调，并在推理过程中共同发挥作用，以实现最佳性能。

Transformer 深度学习架构

LLM (Large Language Model) 是怎么来的？ 或者 从何而来？

简单来说，LLM (Large Language Model) 是通过深度学习得到的。

LLM (Large Language Model) 是指由大量参数组成的神经网络模型，用于自然语言处理任务，例如文本生成、语言理解等。

通常情况下，LLM基于Transformer架构构建，GPT系列模型就是基于Transformer的架构。

因此，LLM和Transformer之间存在密切的关联，LLM通常是Transformer的一种具体实现。

什么是Transformer？

Transformer是一种常用于构建语言模型的深度学习架构，它采用自注意力机制来处理序列数据，被广泛应用于机器翻译、文本生成等任务中。

2018年10月，Google发出一篇论文 《BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding》BERT模型横空出世，并横扫NLP领域11项任务的最佳成绩!

而在BERT中发表重要作用的结构就是Transformer，之后又相继出现XLNET，roBERT等模型击败了BERT，但是他们的核心没有变，任然是：Transformer

Transformer 网络架构架构由 Ashish Vaswani 等人在 Attention Is All You Need一文中提出，并用于机器翻译任务，和以往网络架构有所区别的是，该网络架构中，编码器和解码器没有采用 RNN 或 CNN 等网络架构，而是采用完全依赖于注意力机制的架构。

Transformer改进了RNN被人诟病的训练慢的特点，利用self-attention可以实现快速并行，Transformer网络架构如下所示：

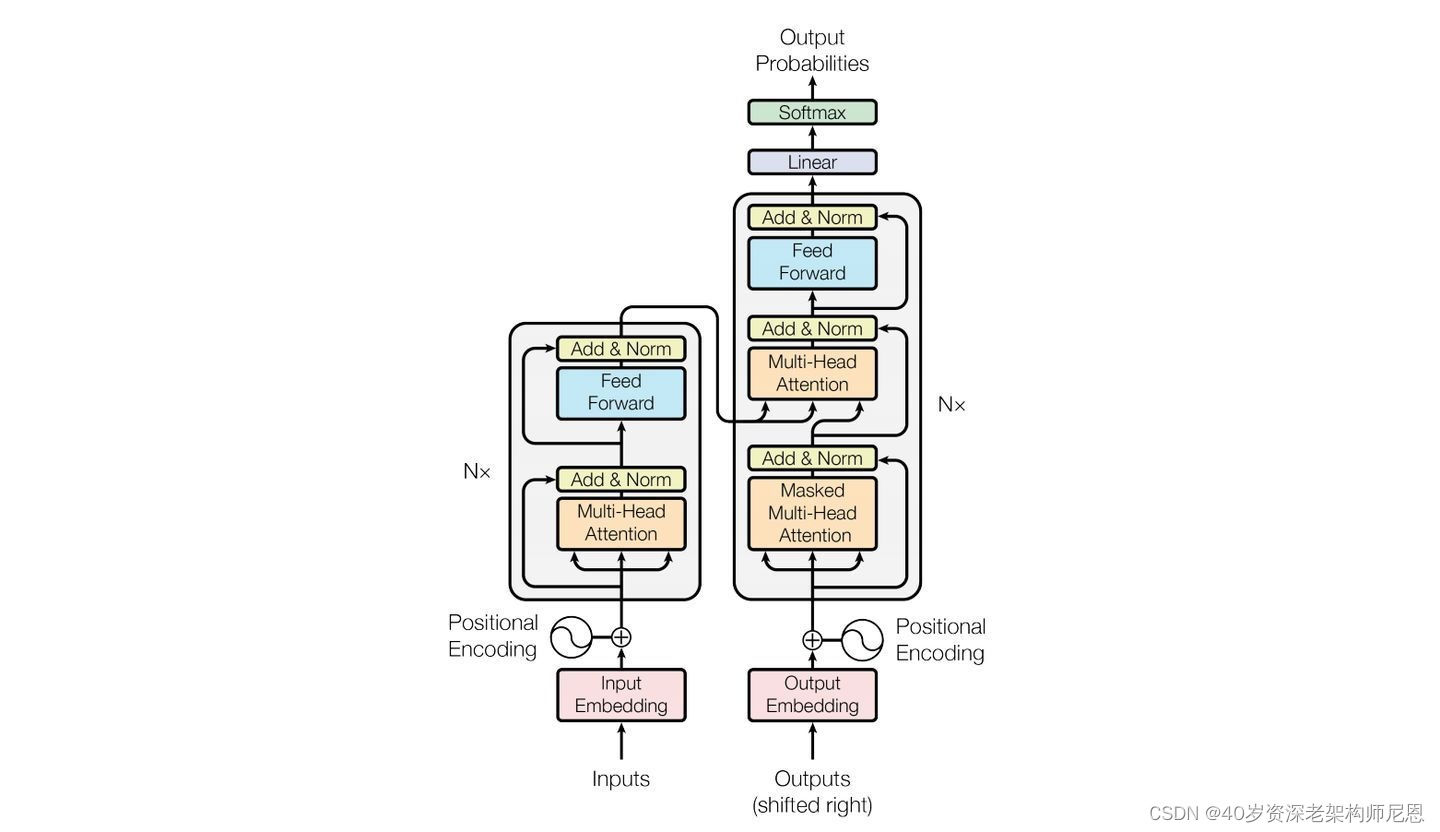
张量（Tensor）

对于AI小白来说，咱们还是从最为基础的 大模型 数据类型开始讲起。

和Java中的基础操作类型 是Object类似的， LLM中，基本的操作数据类型，是张量。

张量（Tensor）是一种数学概念，在机器学习和深度学习领域中经常被使用。在数学上，张量可以理解为多维数组或矩阵的推广。

标量是0维张量，向量是1维张量，矩阵是2维张量

而在深度学习中，我们经常处理的是高维张量，它们可以是3维、4维甚至更高维的数组。

在深度学习中，张量通常用来表示数据、权重和偏差等。

例如，图像可以表示为三维张量，其中的每个维度分别表示图像的高度、宽度和通道数（例如RGB颜色通道）。

神经网络的层级和操作也可以被表示为张量操作，这样就可以在整个网络中传递和处理数据。

因此，张量在深度学习中扮演了非常重要的角色。

张量和矩阵的关系，可以说矩阵是二维张量的一种特殊情况。

具体来说：

1. 矩阵是二维张量：在数学上，矩阵可以被认为是一个二维的数组，它包含行和列。因此，矩阵可以被看作是一个二维张量。
2. 张量是矩阵的推广：张量可以是任意维度的数组，而不仅限于二维。因此，张量是对矩阵概念的推广，它可以是零维（标量）、一维（向量）、二维（矩阵），以及更高维度的数组。
3. 张量包含了更多的信息：相对于矩阵而言，张量可以容纳更多的维度信息，因此在处理更加复杂的数据结构时更加灵活。

总之，可以将矩阵看作是二维张量的一种特殊情况，而张量则是对矩阵概念的推广，可以表示更加丰富和复杂的数据结构。

张量之间的点积运算矩阵乘积运算

在数学和深度学习领域中，张量的相乘通常涉及到张量之间的点积（内积）运算或张量与矩阵的乘法运算。

下面将分别介绍这两种情况：

• 张量之间的点积运算
• 张量与矩阵的乘法运算

张量之间的点积运算：

以二维张量为例。如果两个二维张量具有相同的形状（例如都是形状为 (a, b) 的张量），那么它们之间的点积运算就等同于矩阵之间的点积运算。

点积dot product（又叫内积、数量积）

设二维空间内有两个向量 和 ，定义它们的数量积（又叫内积、点积）为以下实数：

更一般地，n维向量的内积定义如下：

张量之间的乘法运算

张量与张量的乘法运算 是将张量与张量相乘。

张量之间的乘法运算，通常需要考虑张量之间的形状是否兼容。

以二维张量（矩阵）为例。

设A为 的矩阵，B为 的矩阵，那么称 的矩阵C为矩阵A与B的乘积，记作 ，

其中矩阵C中的第 行第 列元素可以表示为：

矩阵相乘的前提条件：

矩阵A 的形状是，矩阵B 的形状是，C 的形状是

有两个矩阵A, B如下：

矩阵A的维数为3x2，矩阵B的维数为2x3，那么A、B相乘的结果矩阵C应该为3x3，其中m=3，p=2，n=3

根据公式，其中i, j取值范围为[1, 3], p=2

得出矩阵C各个元素为如下表格

即矩阵C为3x3的矩阵

简单地记： 结果矩阵C的第(i, j)个元素为矩阵A的第 i 行与矩阵B的第 j 列分别相乘后求和的结果。

需要注意的是，在实际的深度学习任务中，通常会使用专门优化过的张量库（如TensorFlow或PyTorch），这些库提供了高效的张量操作和广泛的运算支持，使得对于多维张量的操作更加简洁和高效

大模型的架构

大型语言模型（LLM）通常采用 Transformer 架构。

Transformer的中文翻译是“变换器”或“转换器”。

Transformer是一种深度学习模型架构，最初由Vaswani等人在2017年的论文中提出，用于自然语言处理任务，如机器翻译。

随后，Transformer架构被广泛应用于各种语言任务，并成为许多大型语言模型（如GPT系列、BERT等）的基础。

Transformer架构的核心是自注意力机制（self-attention mechanism），它使得模型能够同时考虑输入序列中的所有位置，从而在处理长距离依赖关系时表现出色。此外，Transformer还包括位置编码（position encoding）和前馈神经网络（feedforward neural network）等组件。

大型语言模型通常会对Transformer架构进行扩展和改进，以处理更大的数据集和更复杂的语言任务。

例如，GPT系列模型将Transformer架构与自监督学习相结合，通过对大规模文本数据进行预训练，从而使模型具有广泛的语言理解和生成能力。

总的来说，大型语言模型的架构基于Transformer，但会根据具体任务和性能需求进行调整和扩展，以实现更好的性能和效果。在LLM出现之前，基于 神经网络的 机器学习 训练 受到相对较小的数据集的限制，并且对于上下文理解的能力非常有限。这意味着早期的模型无法像人类一样理解文本。

当这篇论文首次发表时，其旨在用于训练语言翻译模型。然而，OpenAI团队发现变压器架构是字符预测的关键解决方案。一旦在整个互联网数据上进行了训练，该模型有可能理解任何文本的上下文，并且能够像人类一样连贯地完成任何句子。

以下是一个图示，展示了模型训练过程中发生的情况：

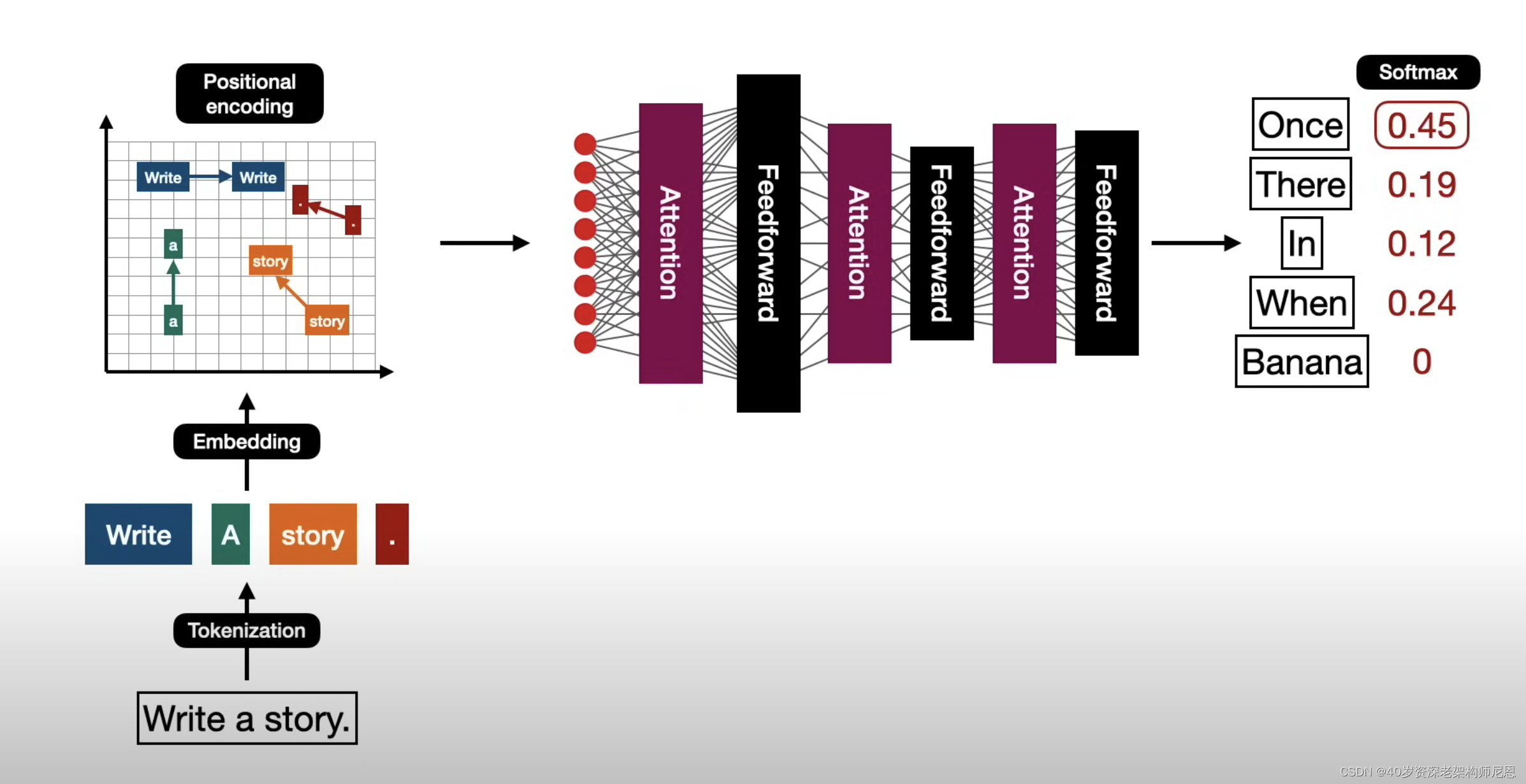
Transformer由论文《Attention is All You Need》提出，现在是谷歌云TPU推荐的参考模型。

论文相关的Tensorflow的代码可以从GitHub获取，其作为Tensor2Tensor包的一部分。

哈佛的NLP团队也实现了一个基于PyTorch的版本，并注释该论文。

在本文中，我们将试图把模型简化一点，并逐一介绍里面的核心概念，希望让普通读者也能轻易理解。

Attention is All You Need：Attention Is All You Need

Transformer 整体结构

首先介绍 Transformer 的整体结构，下面以 一个简单的翻译实例进行说明。

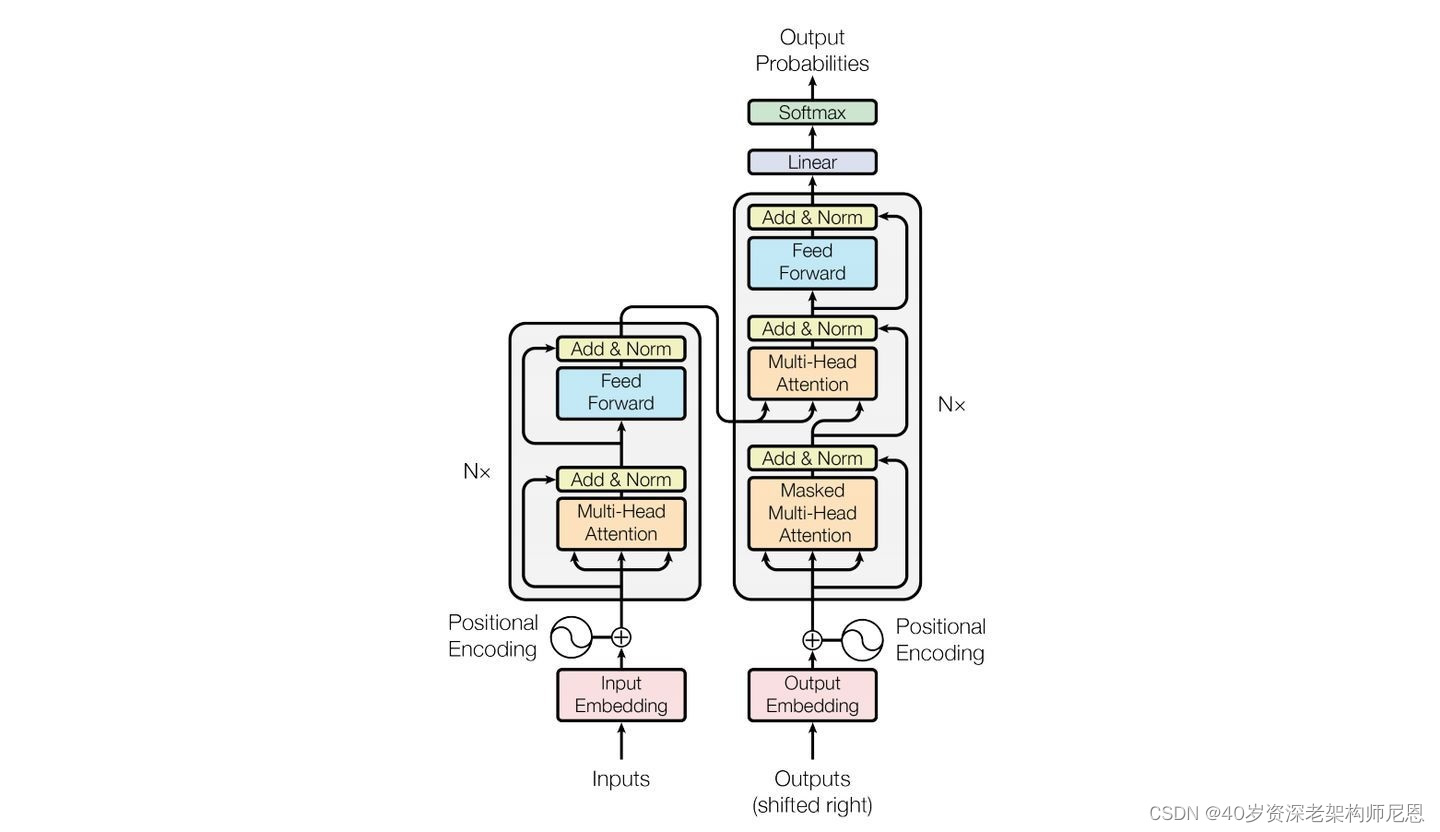
简单梳理一下，大概包括下面的几个部分：

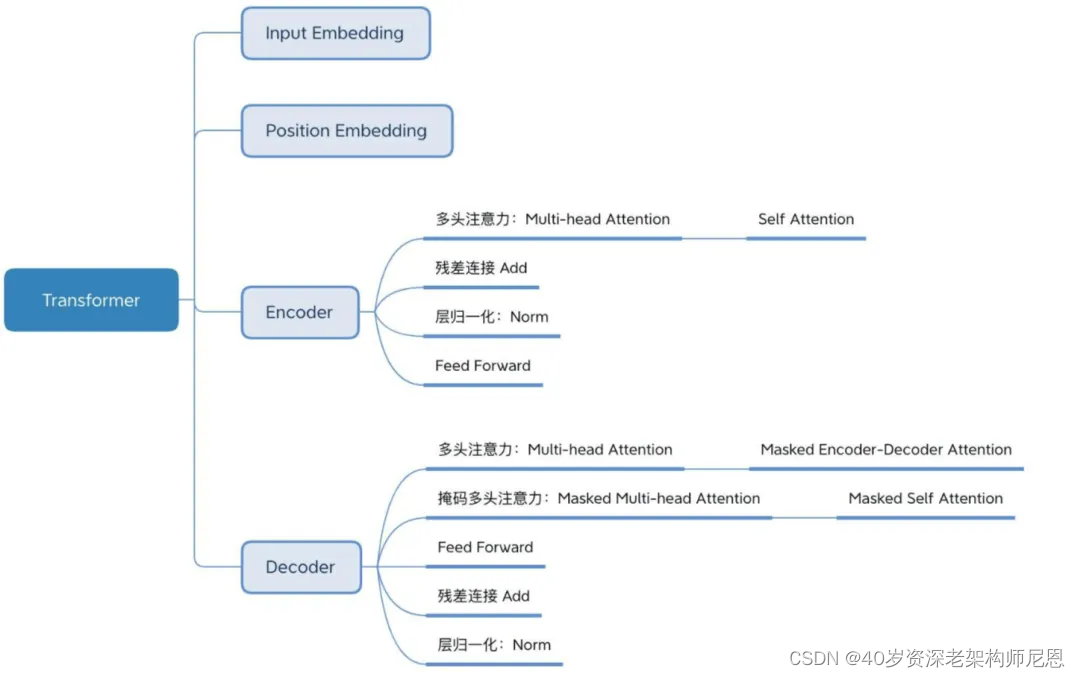
上的图，如果大家看不懂， 是没有关系的。

这篇文章有3万多字， 咱们刚开始看呢？等看完了，大家都懂了。

让我们首先把 Transformer 模型看作一个黑盒子。 在机器翻译应用中，它会接收一种语言的句子，并输出其在另一种语言中的翻译。

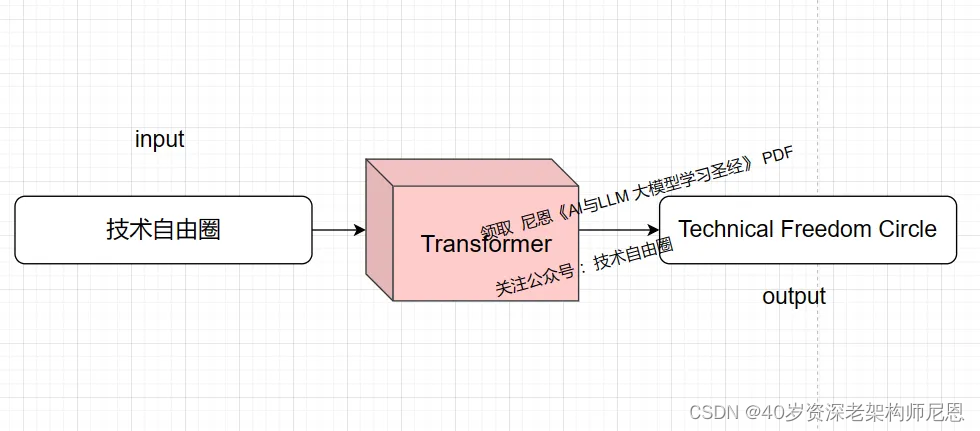
中文 "技术自由圈"的翻译，可以是 “Technical Freedom Circle”

那么，Transformer 怎么进行这种翻译呢？下图是 Transformer 用于中英文翻译的整体结构：

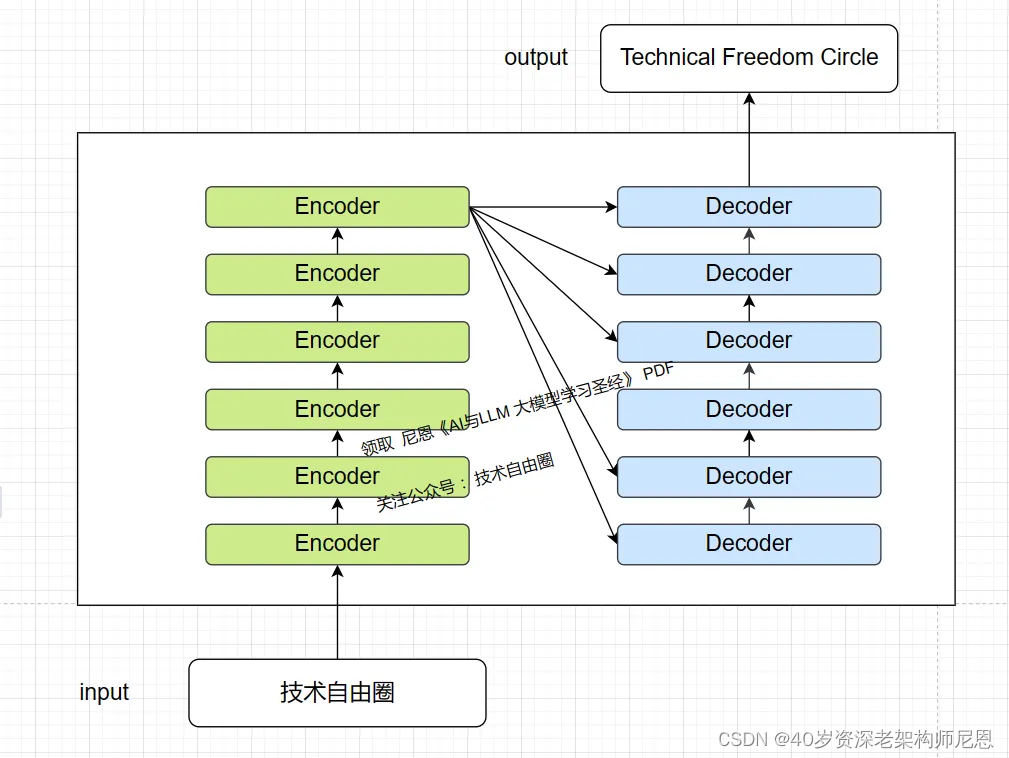
从图可以看到 Transformer 的整体结构，由 Encoder 和 Decoder 两个部分组成，

左边是 Encoder 编码器， 右边是 Decoder 解码器，Encoder 和 Decoder 都包含 6 个 block。

每个编码器都分为两个子层：

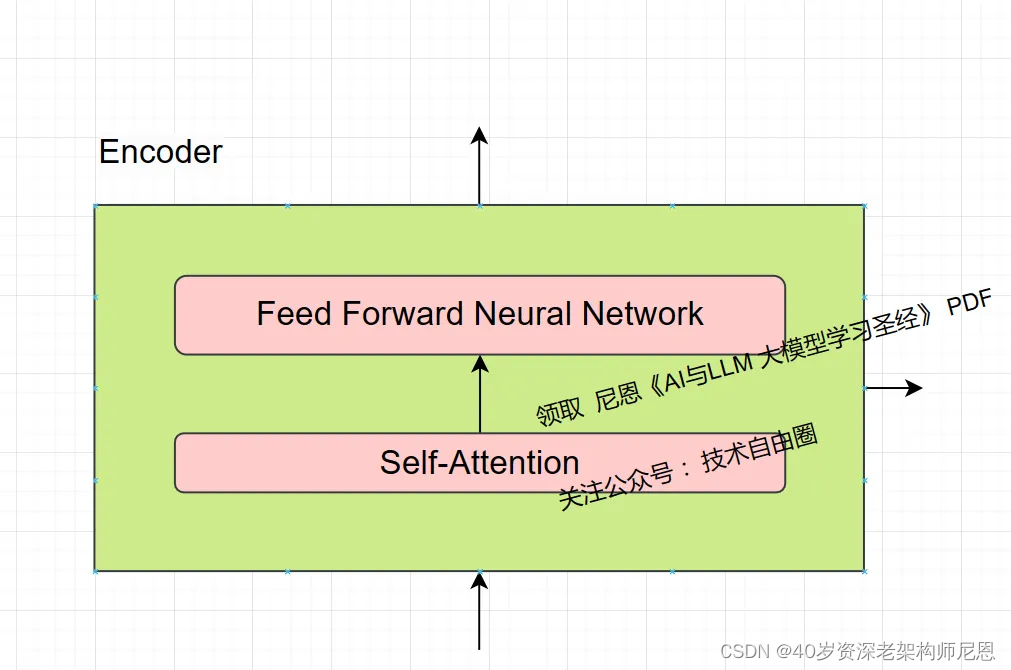
一个编码器在结构上都是相同的（但它们不共享权重）， 包括两个子层，具体如下：

• 自注意力层：在这一层，每个词会观察周围的词，以找出与自己相关的上下文信息。

  编码器的输入首先通过一个自注意力层流过 ，自注意力层 帮助编码器在编码特定词语时，同时关注输入句子的中其他分词。

  换句话说，自注意力层使模型能够关注序列中不同位置之间的关系（上下文信息），而不是简单地按顺序逐个处理。每个位置的输出都可以同时受到其他位置的影响，从而帮助模型更好地理解整个序列。

  有关自注意力层 详细内容，稍后，尼恩再给大家展开介绍。

• 前馈神经网络 层：在这一层，每个词会根据自己收集到的上下文信息，进行信息的整合和处理。

  自注意力层的输出被馈送到一个前馈神经网络，完全相同的前馈网络被独立地应用到每个位置。

  前馈神经网络层是一种由多个神经元组成的基本神经网络结构，用于对输入数据进行加权求和并通过激活函数处理，以产生输出。

  前馈层由神经元组成，这些神经元是可以计算其输入加权和的数学函数。前馈层之所以强大，是因为它有大量的连接。例如，GPT-3 的前馈层规模很大：输出层有 12288 个神经元（对应模型的 12288 维词向量），隐藏层有 49152 个神经元。

  有关前馈神经网络 层 详细内容，稍后，尼恩再给大家展开介绍。

每个Decoder解码器都分为三个子层，具体如下图：

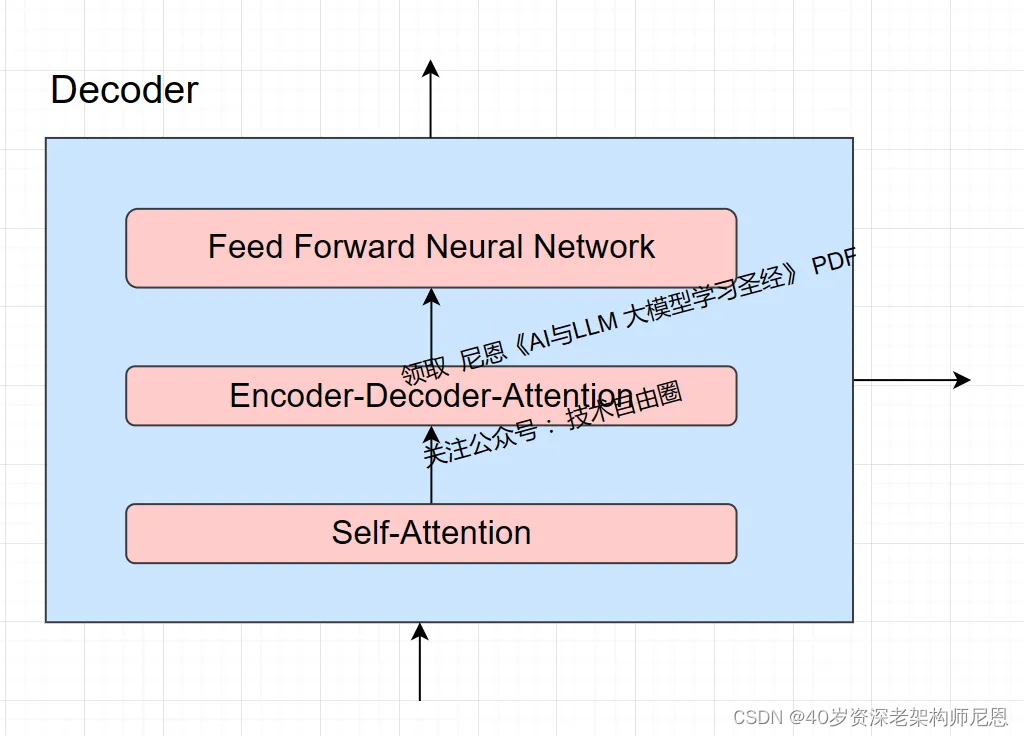
每个Decoder解码器三个子层，具体如下：

• 自注意力层：在这一层，每个词会观察周围的词，以找出与自己相关的上下文信息。

• Encoder-Decoder-Attention（编码器-解码器-注意力）层：注意力机制允许解码器在生成目标序列的每个元素时，动态地关注输入序列的不同部分。这使得解码器能够更有效地利用输入序列的信息，提高翻译或生成的质量。

• 前馈神经网络 层：在这一层，每个词会根据自己收集到的上下文信息，进行信息的整合和处理。

40岁老架构师尼恩提示：大模型比较难，功力浅的不容易懂。 这部分内容如果不懂，可以稍后去学习技术自由圈社群对应的配套视频《从0到1穿透LLM大模型架构》，具体请参见尼恩的公号，技术自由圈

Transformer 的工作流程

现在我们已经了解了模型的主要组件，让我们开始看看各种向量/张量以及它们在这些组件之间是如何流动的，以将经过训练的模型的输入转换为输出。

Transformer 的工作流程大体如下：

**第一步：**获取输入句子的每一个分词的表示向量 X。

表示向量X分为两个部分：

• 分词的 Embedding（Embedding就是从原始数据提取出来的Feature）
• 分词位置 Embedding （位置 Feature）相加得到。

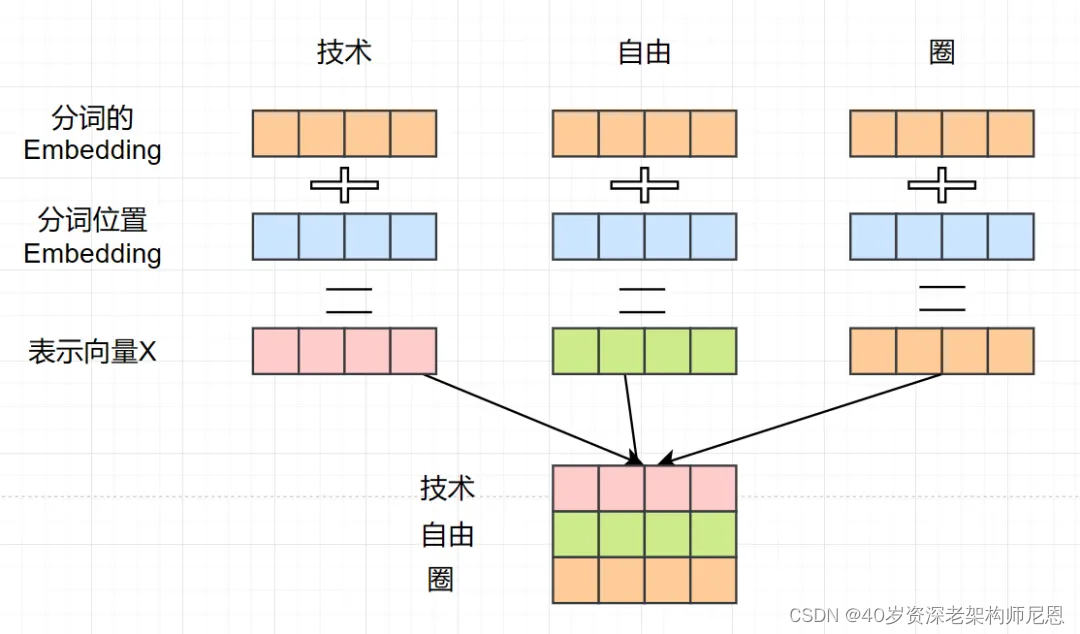
这些表示向量放一起，组合成一个 X 的向量矩阵。 如上图所示，每一行是一个分词的表示向量X。

这里，分词向量矩阵用 X[n,d]表示， n 是句子中分词个数，d 是表示向量的维度 (d=4)。

上面的例子， X[3,4]， 3 是句子中分词个数，4 是表示向量的维度。

ChatGPT 的 Embedding 向量维度，可以在数百到数千之间，具体取决于模型的规模和复杂性。

例如，对于较小规模的 ChatGPT 模型，可能会选择较低维度的 Embedding 向量，如 256 维或 512 维。而对于更大规模的 ChatGPT 模型，Embedding 向量的维度可能会更高，如 1024 维或 2048 维。

另外，Embedding 向量的维度在 ChatGPT 中是一个可以调整的超参数，通常会根据模型的性能和资源的可用性进行优化选择。维度取决于模型的配置和训练过程中的超参数设置。

一步登天，从小白到AI架构。对于AI小白来说，这里有个基础的概念： 什么是嵌入（Embedding）Embedding？

在人工智能中，嵌入（Embedding）Embedding就是从原始数据提取出来的特征向量（Feature）。

嵌入（Embedding）的直观意思是将高维度的离散数据（如分词、字符、类别等）映射到低维度的连续向量空间中。这种映射使得原始数据可以在向量空间中表示为密集的、连续的向量，而不是稀疏的、离散的表示。

举个例子，对于自然语言处理任务，我们可以使用嵌入技术将分词映射到低维度的向量空间中。这样做的好处是可以捕捉分词之间的语义相似性和关联性，使得模型能够更好地理解和处理自然语言文本。

嵌入在图像处理、推荐系统、序列建模等领域也有广泛的应用。它们可以帮助模型更好地理解和表示数据，从而提高模型的性能和泛化能力。嵌入（Embedding）实例非常之多：

1. 词嵌入（Word Embedding）：在自然语言处理任务中，词嵌入是将分词映射到低维度的向量空间中的常见技术。例如，使用词嵌入技术可以将每个分词表示为一个具有固定长度的向量，使得模型能够更好地理解分词之间的语义关系和上下文信息。
2. 图像嵌入（Image Embedding）：在图像处理任务中，图像嵌入是将图像映射到低维度的向量空间中的技术。通过图像嵌入，可以将每个图像表示为一个连续的向量，使得模型能够更好地理解图像的语义信息和特征。
3. 用户嵌入（User Embedding）：在推荐系统中，用户嵌入是将用户映射到低维度的向量空间中的技术。User Embedding将用户的特征和行为映射到一个低维度的向量空间中，以便机器学习模型能够更好地理解和处理用户的特征和行为。通过用户嵌入，可以将用户的偏好和行为表示为一个向量，从而帮助模型更好地理解用户的兴趣和需求，提高推荐的准确性。User Embedding 嵌入可以帮助模型更好地理解用户之间的相似性和差异性，从而提高模型在个性化推荐、用户分类等任务上的性能。

这些是嵌入在人工智能中常见的实例，它们可以帮助模型更好地理解和表示数据，从而提高模型的性能和泛化能力。

第二步： 通过Encoders，将表示向量矩阵 X, 编码成为 编码 矩阵 Y。

将得到的分词表示向量矩阵作为input， 传入 Encoders中，经过 6 个 Encoder block 后可以得到句子所有分词的编码信息矩阵 Y，如下图。

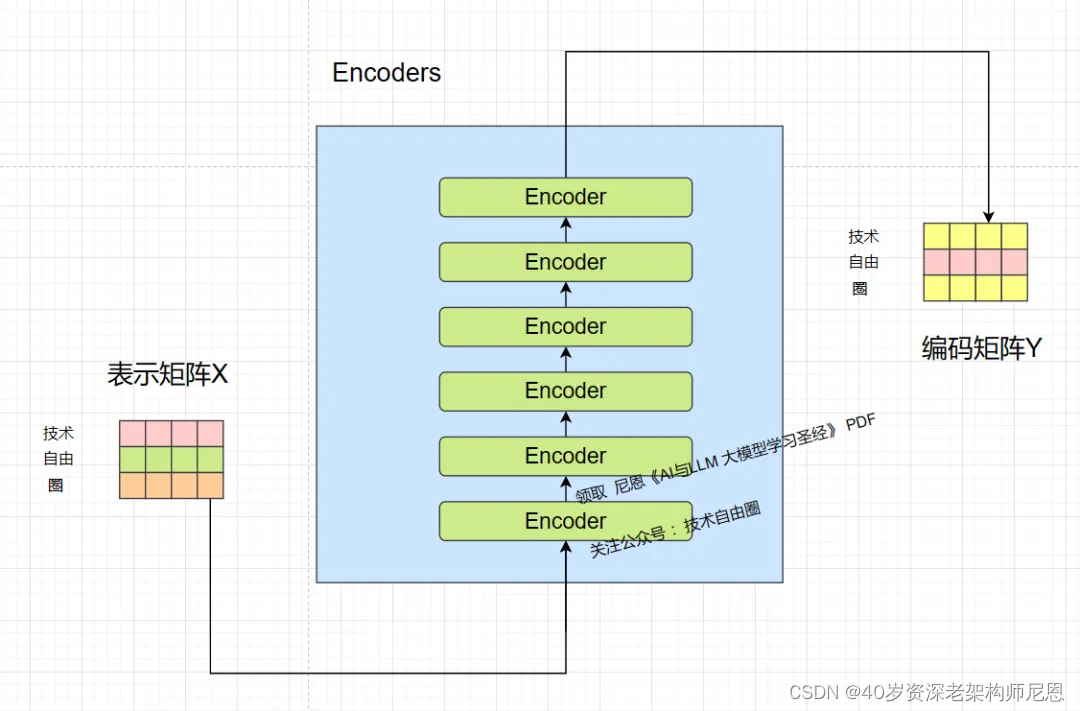
分词向量矩阵用 X[n,d]表示， n 是句子中分词个数，d 是表示向量的维度 (d=4)。

上图中，每一个 Encoder block 输出的矩阵，在维度上，与输入矩阵完全一致。

第三步：通过Decoders 将编码矩阵Y, 依次解码为一个一个的目标分词。

将 Encoder 输出的 编码矩阵Y传递到 Decoders 中，Decoders 依次会根据当前翻译过的分词 1~ i ，翻译出一个分词 i+1。

Decoders 接收了 Encoder 的编码矩阵 编码矩阵Y，然后首先输入一个 “翻译开始符”，预测第一个分词"技术"， 翻译的结果是 "Technical "

第一个分词的翻译过程，如下图：

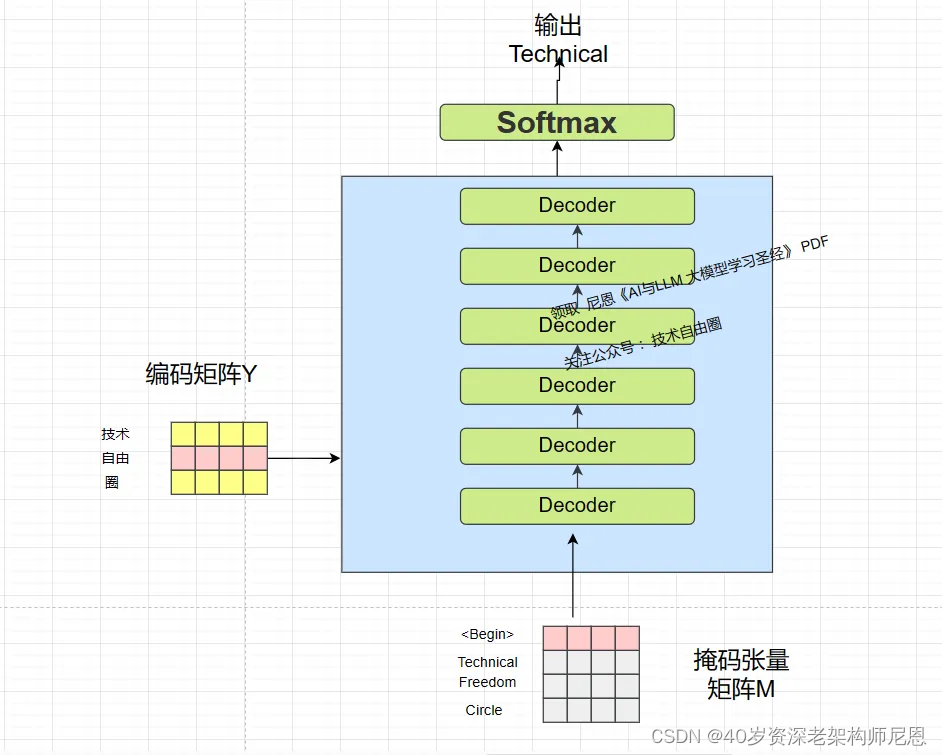
中文 "技术自由圈"的翻译，可以是 “Technical Freedom Circle”

然后输入 “翻译开始符” 和分词 “技术”，预测分词 “自由”， 翻译的结果是 "Freedom " 。

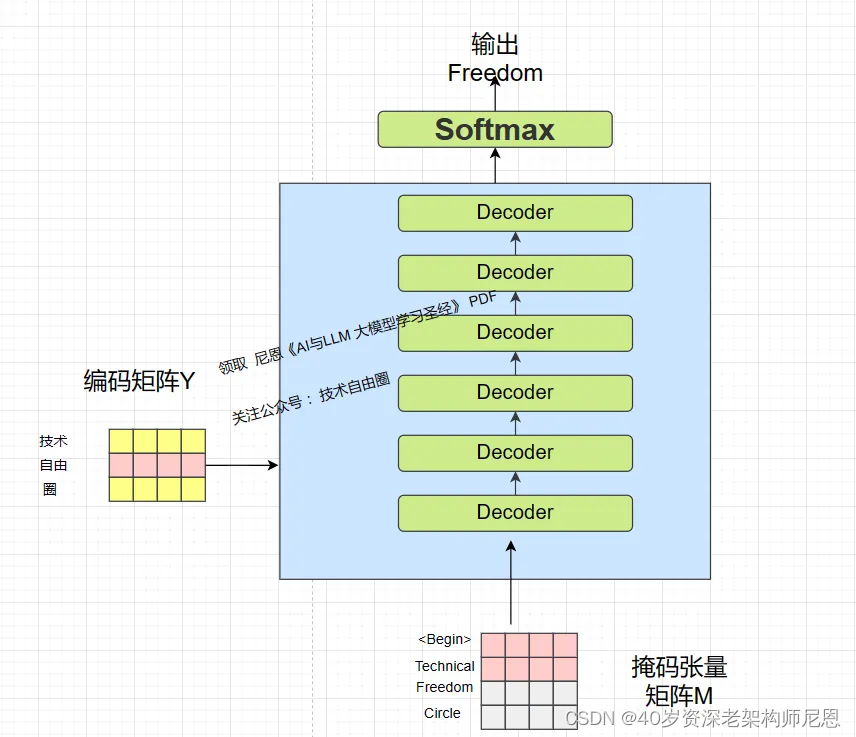
以此类推，然后输入翻译开始符 “” 和分词 “技术”， 分词 “自由”，预测分词 “圈”，以此类推。

在翻译的过程中，翻译到分词 i+1 的时候需要通过 Mask矩阵（更准确的说是 掩码张量） 遮盖住 i+1 之后的分词。

Transformer 的流程总结

到此， Transformer 翻译中文 “技术自由圈”,结果是 “Technical Freedom Circle”

这是 Transformer 使用时候的大致流程，就是下面的三步。

• 第一步：获取输入句子的每一个分词的表示向量 X。

• 第二步：通过Encoders，将表示向量矩阵 X, 编码成为 编码 矩阵 Y。

• 第三步：通过Decoders 将编码矩阵Y, 依次解码为一个一个的目标分词， 就是咱们的翻译目标。

由粗入细，由潜入深，接下来，咱们一步一步的进入细节。

Transformer 的输入

Transformer 中分词的输入表示 x由分词 Embedding 和位置 Embedding （Positional Encoding）相加得到。

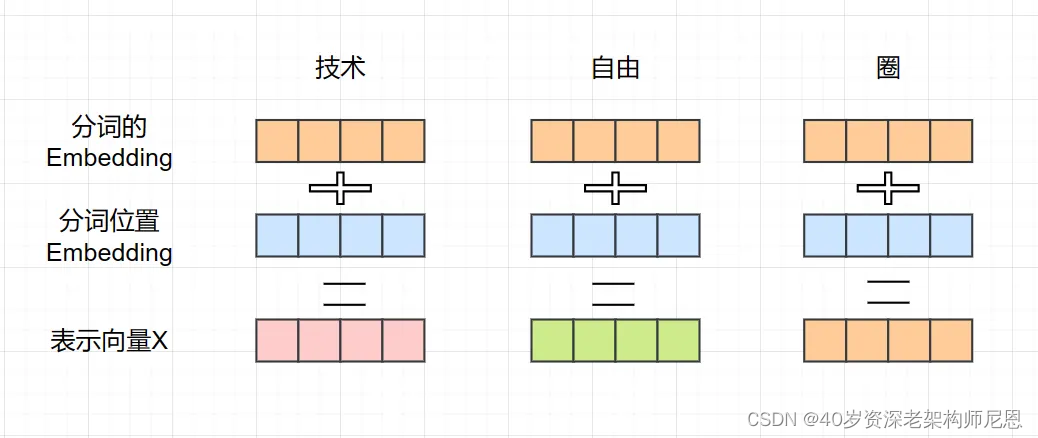
step1：获取分词的嵌入（Embedding）特征张量

嵌入（Embedding）是将离散的符号（如单词、字符、类别等）映射到连续向量空间的过程。嵌入是将高维离散特征转换为低维连续特征的一种方式，这种转换有助于提取序列数据中的语义和上下文信息，从而改善序列模型的性能。

分词的嵌入（Embedding）特征张量 有很多种方式可以获取，具体取决于你所使用的分词工具、语言和需求。以下是一些常见的获取分词嵌入的方式。

分词的嵌入（Embedding）特征张量，通常用于自然语言处理（NLP）和推荐系统等任务，其中输入数据通常是符号序列。通过嵌入，每个符号（例如单词）被映射为一个稠密向量，这个向量可以捕捉到符号的语义和语境信息。

在下面列出了 分词的嵌入（Embedding）特征张量 的一些重要应用场景：

1. 自然语言处理（NLP）：在文本处理任务中，嵌入可以将单词或字符映射到连续的向量表示，使得模型能够捕获词语之间的语义关系和上下文信息。Word2Vec、GloVe和BERT等模型都使用了嵌入技术。
2. 推荐系统：在推荐系统中，嵌入可以用于表示用户和物品（如商品、电影等），从而构建用户-物品交互矩阵的表示。这种表示可以用于预测用户对未知物品的兴趣。
3. 时间序列预测：对于时间序列数据，嵌入可以用于将时间步和历史数据映射为连续向量，以捕获序列中的趋势和模式。
4. 序列标注：在序列标注任务中，嵌入可以用于将输入的序列元素（如字母、音素等）映射为向量，供序列标注模型使用。
5. 图像描述生成：在图像描述生成任务中，嵌入可以将图像中的对象或场景映射为向量，作为生成描述的输入。

方式一：使用 PyTorch嵌入层的进行特征提取

当使用 PyTorch 进行文本数据的特征提取时，可以使用嵌入层来将单词映射为连续向量表示。

40岁老架构师尼恩提示：这部分后面有实操演示，可以稍后去学习技术自由圈社群对应的配套视频《从0到1穿透LLM大模型架构》，具体请参见尼恩的公号，技术自由圈

方式二：TensorFlow嵌入层的特征提取

当在 TensorFlow 中使用嵌入层进行文本数据的特征提取时，可以使用 tf.keras.layers.Embedding 层来将单词映射为连续向量表示。以下是一个简单的示例代码，演示了在 TensorFlow 中使用嵌入层进行文本数据的特征提取的过程。

40岁老架构师尼恩提示：这部分后面有实操演示，可以稍后去学习技术自由圈社群对应的配套视频《从0到1穿透LLM大模型架构》，具体请参见尼恩的公号，技术自由圈

方式三：使用Word2Vec深度学习模型 进行特征提取

Word2Vec是一种用于学习词嵌入（word embeddings）的深度学习模型，旨在将词汇映射到低维度的向量空间中。这种映射使得单词的语义信息能够以密集向量的形式被捕捉，这与传统的词袋模型（Bag of Words）或TF-IDF表示形式不同。Word2Vec模型的主要目标是学习具有相似语义含义的词汇之间的相似向量表示。

40岁老架构师尼恩提示：这部分后面有实操演示，可以稍后去学习技术自由圈社群对应的配套视频《从0到1穿透LLM大模型架构》，具体请参见尼恩的公号，技术自由圈

step2：获取 分词的 位置 Embedding 嵌入

Transformer 中除了分词的特征 Embedding，还需要使用位置 Embedding 表示分词出现在句子中的位置。

因为 Transformer 不采用 RNN 的结构，不能利用分词的顺序信息，而是使用全局信息，分词的全局信息信息对于 NLP 来说非常重要。

所以 Transformer 中使用分词向量之间需要有一个相对位置关系，而这 位置 Embedding （位置嵌入向量）保存分词在序列中的相对或绝对位置。位置嵌入 Embedding 用 **PE（position Embedding ）**表示, PE 的维度与分词 Embedding 是一样的。

假设，一种语言每个分词都用一个4的向量表示（长度为4的数组）换句话说，一个分词嵌入成长度为4的向量。

因为位置向量长度要和词向量相加，需要长度保持一致，所以位置向量的维度为也为4。

如何获得PE, 有两种方式：

• 方式一：通过训练得到
• 方式二：使用某种公式计算得到。

在 Transformer 中， 采用了方式二，通过某种公式计算PE 。

Transformer 中，PE（position Embedding ） 计算公式采用sin-cos函数，如下：

其中：

• pos 表示分词在句子中的位置，其中，pos范围是0~N，最长的一句话包含的单词个数为N，pos表示分词在句子里边的位置

• d 表示 PE的维度 (与分词 Embedding 一样)， 上面的例子是 4

• 2i 表示偶数的维度，上面的例子是 维度 0，维度2

• 2i+1 表示奇数维度 (即 2i≤d, 2i+1≤d)， 上面的例子是 维度 1，维度3

以下是一个简单的 Python 示例演示如何实现位置编码：

import numpy as np

def positional_encoding(max_seq_len, d_model):
    position_enc = np.zeros((max_seq_len, d_model))
    for pos in range(max_seq_len):
        for i in range(0, d_model, 2):
            position_enc[pos, i] = np.sin(pos / (10000 ** ((2 * i)/d_model)))
            position_enc[pos, i + 1] = np.cos(pos / (10000 ** ((2 * (i + 1))/d_model)))
    return position_enc

max_seq_len = 10  # 最大序列长度
d_model = 512     # 嵌入维度

# 生成位置编码
pos_enc = positional_encoding(max_seq_len, d_model)
print(pos_enc)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

在这个示例中，我们定义了一个 positional_encoding 函数来生成位置编码矩阵。

该函数接受两个参数：max_seq_len 表示序列的最大长度，d_model 表示嵌入向量的维度。

位置编码矩阵的大小为 (max_seq_len, d_model)。

位置编码的计算方式通常是通过一组固定的公式来计算的。

位置编码计算方法通过在正弦和余弦函数中应用不同的频率来生成位置编码向量。

具体来说，我们通过在正弦函数和余弦函数中应用不同的频率来生成位置编码向量的奇数和偶数索引位置上的值。

最后，将生成的位置编码矩阵打印出来以查看结果。

使用sin-cos函数公式计算 PE 有以下的好处：

• 使 PE 能够适应比训练集里面所有句子更长的句子，假设训练集里面最长的句子是有 20 个分词，突然来了一个长度为 21 的句子，则使用公式计算的方法可以计算出第 21 位的 Embedding。
• 可以让模型容易地计算出相对位置，对于固定长度的间距 k，PE(pos+k) 可以用 PE(pos) 计算得到。因为 Sin(A+B) = Sin(A)Cos(B) + Cos(A)Sin(B), Cos(A+B) = Cos(A)Cos(B) - Sin(A)Sin(B)。

正弦（sine）和余弦（cosine）函数是三角函数中的两个基本函数，通常用于描述周期性现象和振荡运动。它们在数学、工程、物理学等领域都有广泛的应用。

1. 正弦函数（sine function）：

正弦函数是一个周期函数，表示单位圆上一个角的正弦值。在数学中，正弦函数通常用符号 “sin” 表示，其定义为：

sin(α)= 对边/斜边
1

其中，α表示角度，对边表示与角度相对应的直角三角形的斜边的对边（垂直边），斜边表示直角三角形的斜边。
正弦函数的值域为 [−1,1]，在单位圆上，正弦函数的值等于对应角度的点在单位圆上的纵坐标。

正弦函数（sine function）函数图像

2. 余弦函数（cosine function）：‘

   余弦函数也是一个周期函数，表示单位圆上一个角的余弦值。

   在数学中，余弦函数通常用符号 “cos” 表示，其定义为：

     cos⁡(α)= 斜边/斜边
   1

其中，α 表示角度，邻边表示与角度相对应的直角三角形的斜边的邻边（水平边），斜边表示直角三角形的斜边。余弦函数的值域也为 [−1,1]，在单位圆上，余弦函数的值等于对应角度的点在单位圆上的横坐标。

余弦函数（cosine function）函数图像

在实际应用中，正弦和余弦函数被广泛用于描述振动、波动、周期性运动等现象。它们在工程学、物理学、信号处理、图像处理等领域都有重要的应用。

因为sin cos是一个单位圆的概念，两个构成了一个单位圆，对sin cos对的理解，可以比喻成一个时钟的分针和时针。

Positonal Embedding 是在每两个维度中指定了一个时钟指针，

然后呢，如果想要另一个的Positional Embedding信息的话，我们可以去调这个时钟的指针，让他调整到下一个位置去

首先我们先引入一个例子，比如说我们要表示二进制数字，用16进制表示，

这些二进制数字，你可以看出来他们是有规律的，

• 最低位会随着每一个数字变化而变化，
• 第二低的位会随着每两个数的变化而变化，
• 如此类推

二进制数字，相当于把一个连续的数字变为了有规律的离散的量！

但是，二进制对表示无穷无尽的浮点数，不是很好表示，所以我们这里使用了 正弦函数！

二进制数字 使用二进制函数的交替信息，其实PE用正弦函数也是用了这种二进制的思想，

正弦函数是有一定的规律性的，有周期性的，这正好符合了二进制数字表示方式这种的规律性，

所以，我们这边用正弦函数来表示距离，也是一个模仿二进制表示法的方式;

下面的例子，来自于 文献：Transformer Architecture: The Positional Encoding - Amirhossein Kazemnejad’s Blog

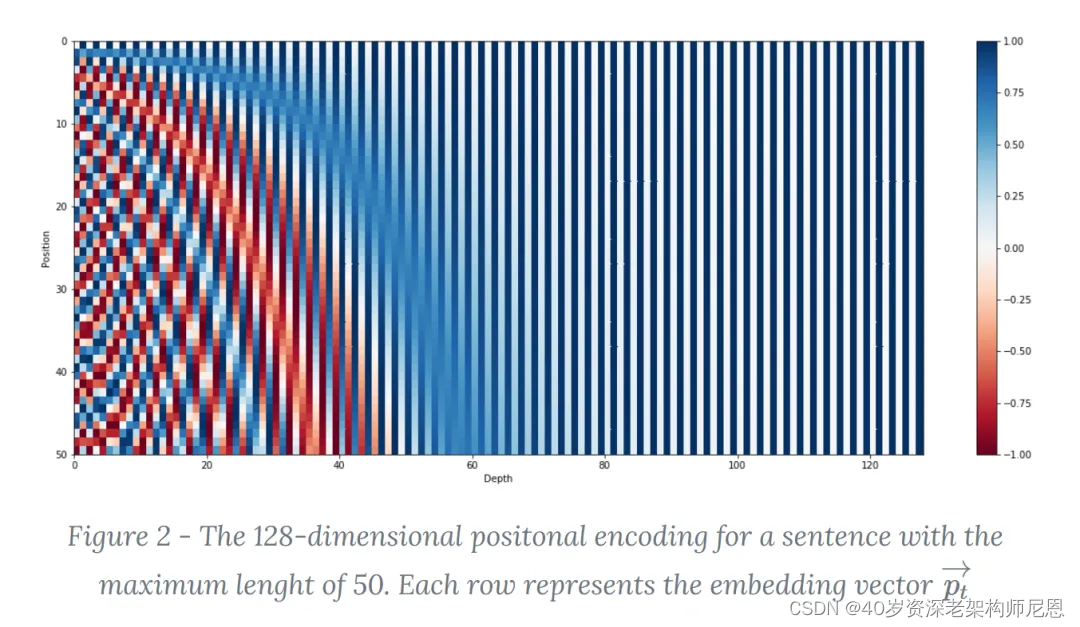
这个是一个长度为50个分词的句子，每一个分词的每一个维度所代表的 PE 矩阵。

y方向表示的是位置 position， 纵向是position, 最大之是一个句子的长度，此处是50，说明该句子包含50个单词，即上面的N 。

x方向表示的是 维度向量的index，上图中，每一个分词 的向量维度是128维度，奇数用位置相关的sin值，偶数用位置相关的cos值

比如说第40行，就是表示48个分词的 pt 向量，可以通过这个来表示位置

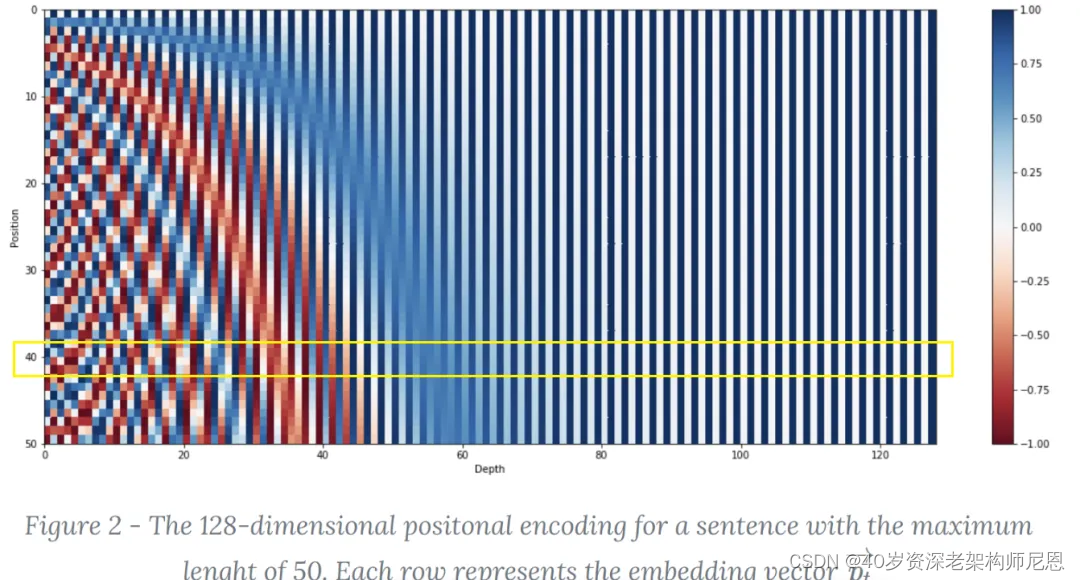
用正弦函数作为这种位置信息的表示，可以让模型快速的学习到 相对位置 这一特征！这就是，为什么为什么sin cos 的组合能方便表示相对位置，

如果说，你已知一个位置的Positional Embedding，想要知道这个位置之后的第k个位置的positional Embedding，可以通过原位置的一个线性函数来求出原位置+k个位置的Positional Encoding

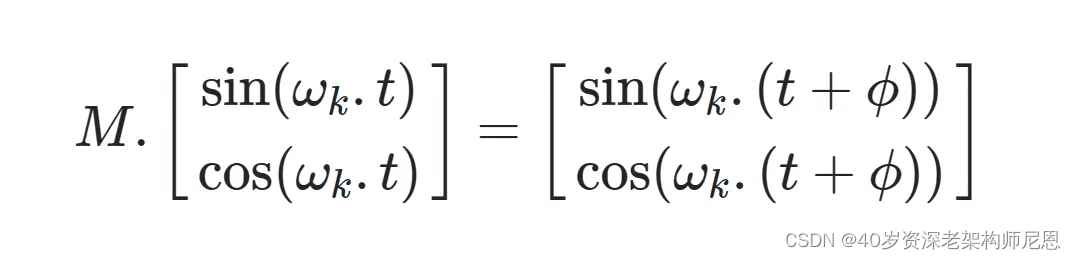
这个M 就是表示线性函数，[sin(wk,t),cos(wk,t)] 表示的是一个sin-cos 对，表示的是第wk个频率所对应的对，可以推广到一个多维度的情况，这里先用低维度的情况来进行证明

证明过程，请参见文献：Transformer Architecture: The Positional Encoding - Amirhossein Kazemnejad’s Blog

将分词的词 Embedding 和位置 Embedding 相加，就可以得到分词的表示向量 x，x 就是 Transformer 的输入。

40岁老架构师尼恩提示：大模型比较难，功力浅的不容易懂。 这部分内容如果不懂，可以稍后去学习技术自由圈社群对应的配套视频《从0到1穿透LLM大模型架构》，具体请参见尼恩的公号，技术自由圈

Self-Attention（自注意力机制）

Transformer Encoder 和 Decoder

上图是论文中 Transformer 的内部结构图，左侧为 Encoder block，右侧为 Decoder block。

红色圈中的部分为 Multi-Head Attention，是由多个 Self-Attention组成的，可以看到

• Encoder block 包含一个 Multi-Head Attention，
• Decoder block 包含两个 Multi-Head Attention (其中有一个用到 Masked)。

Multi-Head Attention 上方还包括一个 Add & Norm 层，Add和Norm 的功能是：

• Add 表示残差连接 (Residual Connection) ，用于防止网络退化，

• Norm 表示 Layer Normalization（层归一化），用于对每一层的激活值进行归一化。

因为 Self-Attention是 Transformer 的重点，所以我们重点关注 Multi-Head Attention 以及 Self-Attention，首先详细了解一下 Self-Attention 的内部逻辑。

Self-Attention 结构

Self-Attention（自注意力）是一种用于处理序列数据的机制，特别是在深度学习中的Transformer模型中被广泛使用。它的直白解释如下：

1. 关注自身的能力：Self-Attention允许模型在处理输入序列时关注序列中各个位置之间的关系，而不是简单地按顺序逐个处理。
2. 自注意力权重：对于每个输入位置，Self-Attention会计算一个与其他位置的关联程度，称为自注意力权重。这些权重表示了每个位置在整个序列中的重要性。
3. 信息汇聚：通过将每个位置的自注意力权重与相应位置的特征向量相乘，并将结果进行加权求和，可以汇聚输入序列的信息，产生新的表示。
4. 并行计算：Self-Attention可以并行地计算每个位置的自注意力权重，因此在实践中往往具有较高的效率。

总的来说，Self-Attention允许模型在处理序列数据时同时关注不同位置的信息，并根据位置之间的关系来提取和汇聚输入序列的信息，从而更好地理解序列数据并改善模型性能。

缩放点积注意力（Scaled Dot-Product Attention）是Transformer模型中的一种注意力机制，用于计算查询（query）和键（key）之间的相关性，并根据这种相关性对值（value）进行加权。在缩放点积注意力中，通过对点积结果进行缩放，以避免点积过大而导致梯度消失或梯度爆炸的问题。

具体来说，缩放点积注意力的计算过程如下：

1. 对查询（query）和键（key）进行点积运算，得到未缩放的注意力分数。
2. 将未缩放的注意力分数除以一个缩放因子（通常是查询向量的维度的平方根），以控制注意力分数的范围。
3. 将得到的缩放后的注意力分数进行softmax运算，以得到注意力权重。
4. 将注意力权重与值（value）进行加权求和，得到最终的输出。

缩放点积注意力（Scaled Dot-Product Attention），计算的公式如下：

上图是 Self-Attention 的结构，在计算的时候需要用到矩阵Q(查询),K(键值),V(值)。在实际中，Self-Attention 接收的是输入(分词的表示向量x组成的矩阵X) 或者上一个 Encoder block 的输出。而Q,K,V正是通过 Self-Attention 的输入进行线性变换得到的。

缩放点积注意力具有较好的数值稳定性，并且在实践中被广泛应用于自然语言处理任务中，如文本分类、语言模型等。

Self-Attention的查询（query）、键（key）和值（value）

在自注意力（Self-Attention）机制中，每个词（或者其他序列中的元素）都会被用来生成查询（query）、键（key）和值（value）三种表示。

查询（query）、键（key）和值（value）这些表示是 通过的线性变换得到的。以下是它们的简要解释：

1. 查询（Query）：
   • 查询向量是输入序列中每个词的一个线性变换后得到的表示。它表示了当前词的语义信息，并用于计算与其他词的注意力权重。
   • 通常，通过将输入词向量乘以一个权重矩阵（通常是一个可学习的参数）来得到查询向量。
2. 键（Key）：
   • 键向量也是输入序列中每个词的一个线性变换后得到的表示。它与查询向量类似，用于计算当前词与其他词的相关性。
   • 键向量通常也是通过将输入词向量乘以另一个权重矩阵来得到的。
3. 值（Value）：
   • 值向量是用来为当前词提供上下文信息的表示。它是输入序列中每个词的另一个线性变换后得到的表示。
   • 通常，值向量也是通过将输入词向量乘以一个权重矩阵来得到的。

在自注意力机制中，查询、键和值的计算是独立进行的，并且它们的权重矩阵通常是通过模型的学习过程自动学习得到的。

查询和键的相关性用来计算注意力权重，而值则根据这些权重来加权组合以生成最终的输出。

Q, K, V 的计算

Self-Attention 的输入是编码矩阵Y，则可以使用线性变换矩阵WQ,WK,WV计算得到Q,K,V。

计算如下图所示，注意Q, K, V 的每一行都表示一个分词。

技术自由圈的编码矩阵Y，和线性变换矩阵WQ 相乘，得到查询向量矩阵 Q，Q的每一行都表示一个分词。

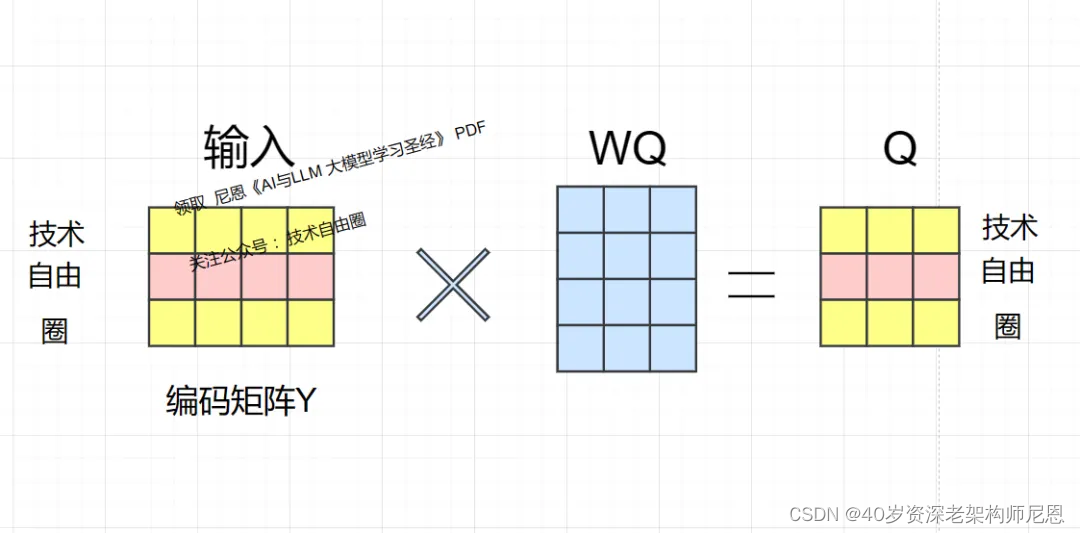
技术自由圈的编码矩阵Y，和线性变换矩阵WK 相乘，得到key键向量矩阵 K，K的每一行都表示一个分词。

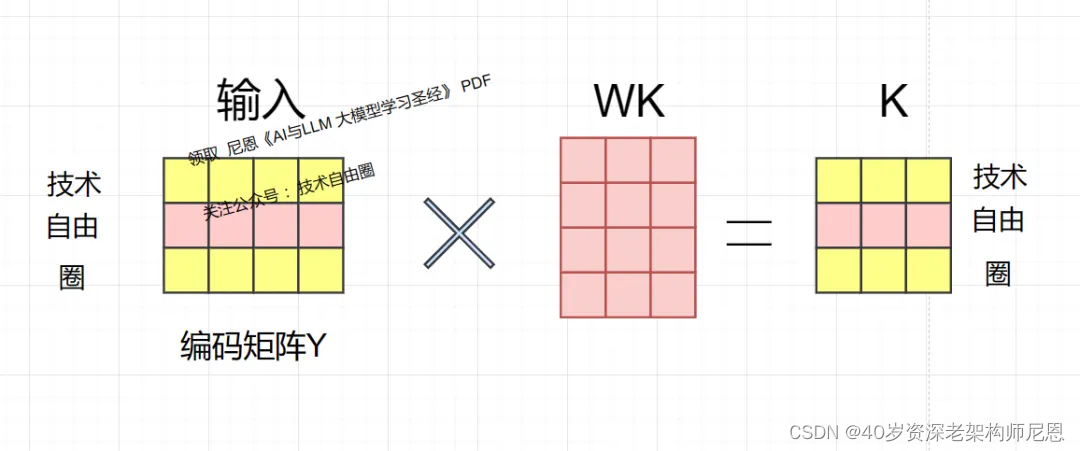
技术自由圈的编码矩阵Y，和线性变换矩阵WK 相乘，得到value值向量矩阵V，V的每一行都表示一个分词。

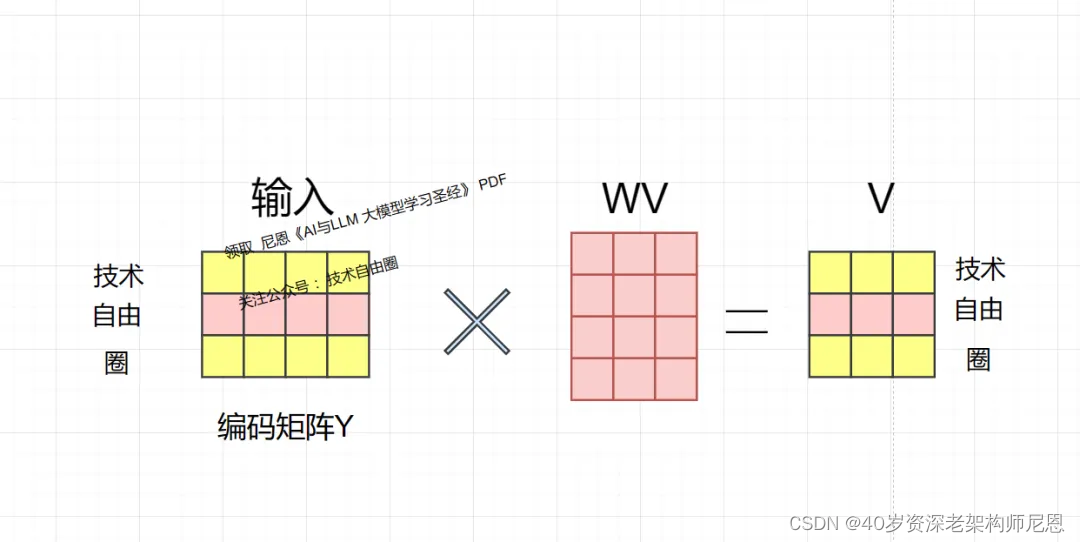
Q, K, V 的计算用到matmu矩阵乘法

matmul 是矩阵乘法的缩写，它是许多数值计算库（如NumPy、TensorFlow、PyTorch等）中常用的函数，用于计算两个矩阵的乘积。

在数学上，给定两个矩阵 A 和 B，它们的乘积 C 的计算如下：

如果 A 是一个形状为 (m, n) 的矩阵，B 是一个形状为 (n, p) 的矩阵，则 C 是一个形状为 (m, p) 的矩阵，其中每个元素 C[i][j] 是矩阵 A 的第 i 行与矩阵 B 的第 j 列的内积（即对应元素相乘后求和）。

在代码中，matmul 函数通常以以下方式使用：

import numpy as np

A = np.array([[1, 2], [3, 4]])  # m x n 矩阵
B = np.array([[5, 6], [7, 8]])  # n x p 矩阵

C = np.matmul(A, B)  # 计算矩阵乘积

print(C)
1
2
3
4
5
6
7
8

这将输出结果：

[[19 22]
 [43 50]]
1
2

值得注意的是，在一些库中，如NumPy，也可以使用 @ 符号来表示矩阵乘法，即 C = A @ B。

WQ,WK,WV 的作用

自注意力公式，也就是缩放点积注意力（Scaled Dot-Product Attention），计算的公式如下：

上图是 Self-Attention 的结构，在计算的时候需要用到矩阵Q(查询),K(键值),V(值)。

Self-Attention 的输入是编码矩阵Y，则可以使用线性变换矩阵WQ,WK,WV计算得到Q,K,V。

Q K V并不是公式中最本质的内容，本质的内容还是 编码矩阵Y

Q K V 究竟是什么？ 其实是 Y的 线性变换，我们看下面的图:

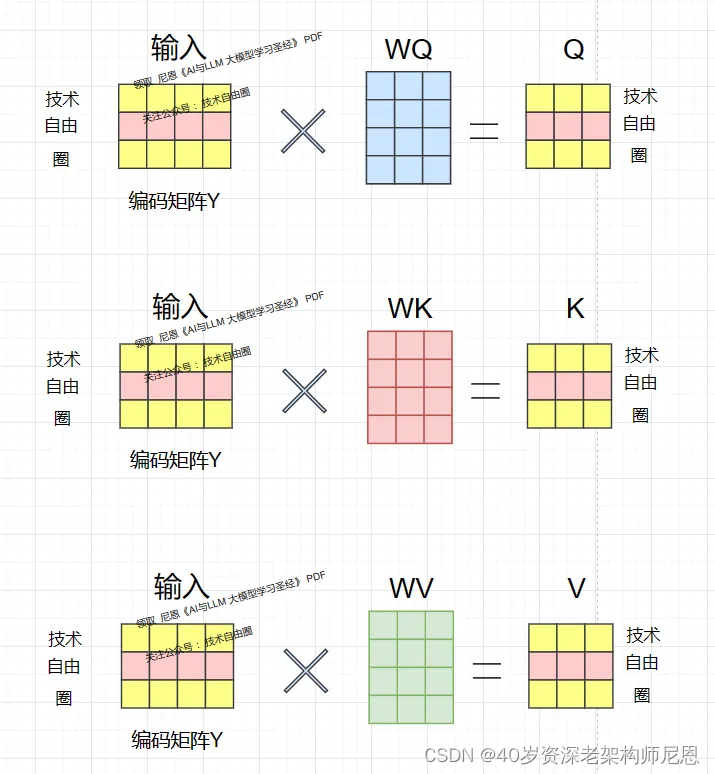
为什么不直接使用 Y 而要对其进行线性变换？

当然是为了提升模型的拟合能力，矩阵 WQ,WK,WV 都是可以训练的，起到一个缓冲的效果。

40岁老架构师尼恩提示：大模型比较难，功力浅的不容易懂。 这部分内容如果不懂，可以稍后去学习技术自由圈社群对应的配套视频《从0到1穿透LLM大模型架构》，具体请参见尼恩的公号，技术自由圈

Q、K相关度原始值、相似度矩阵计算

得到矩阵 Q, K, V之后，就可以计算出 Self-Attention 的输出了，计算的公式如下：

矩阵的转置是将矩阵的行和列对调的操作，即将原矩阵的第i行转换为转置矩阵的第i列，将原矩阵的第j列转换为转置矩阵的第j行。在数学符号中，如果原矩阵为A，转置矩阵为A^T。

转置操作通常表示为A[i][j] = A^T[j][i]。例如，

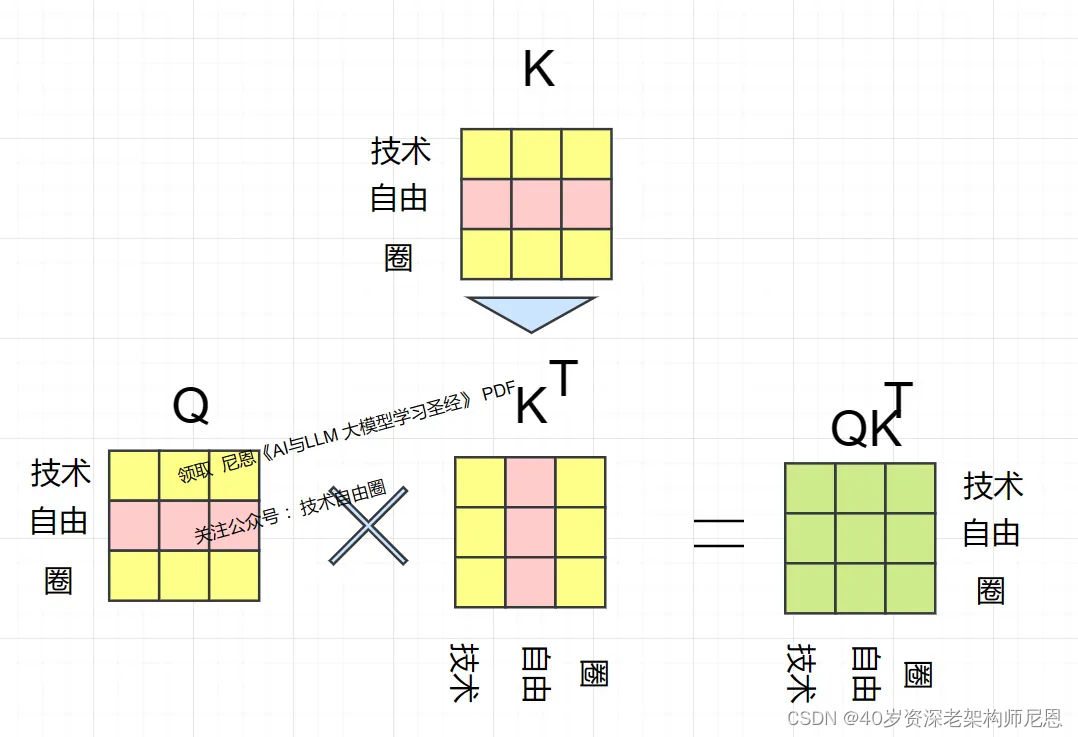
A的 转置矩阵为A^T 如下

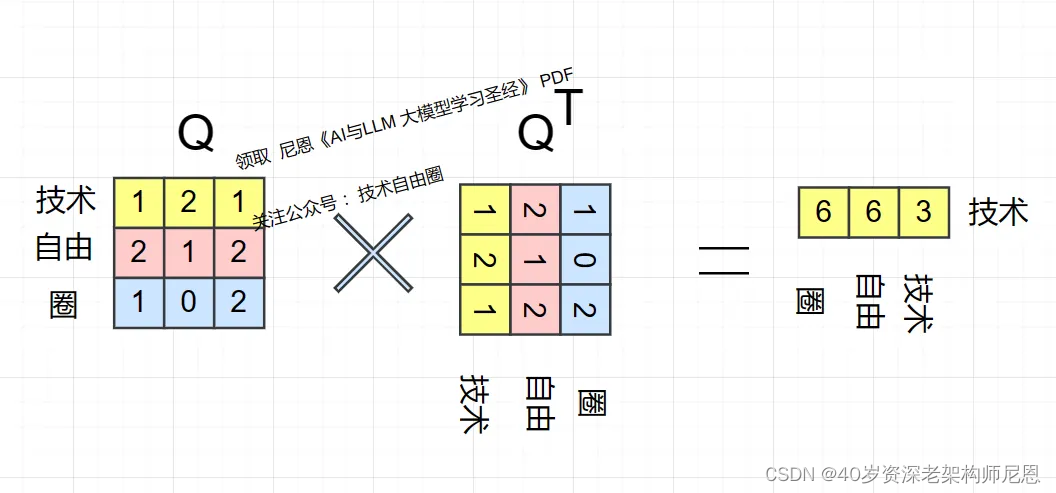
Q乘以K的转置后，得到的矩阵行列数都为 n，n 为句子分词数，这个矩阵可以表示分词之间的 attention 强度。

下图为Q乘以KT（K的转置） ，具体如下：

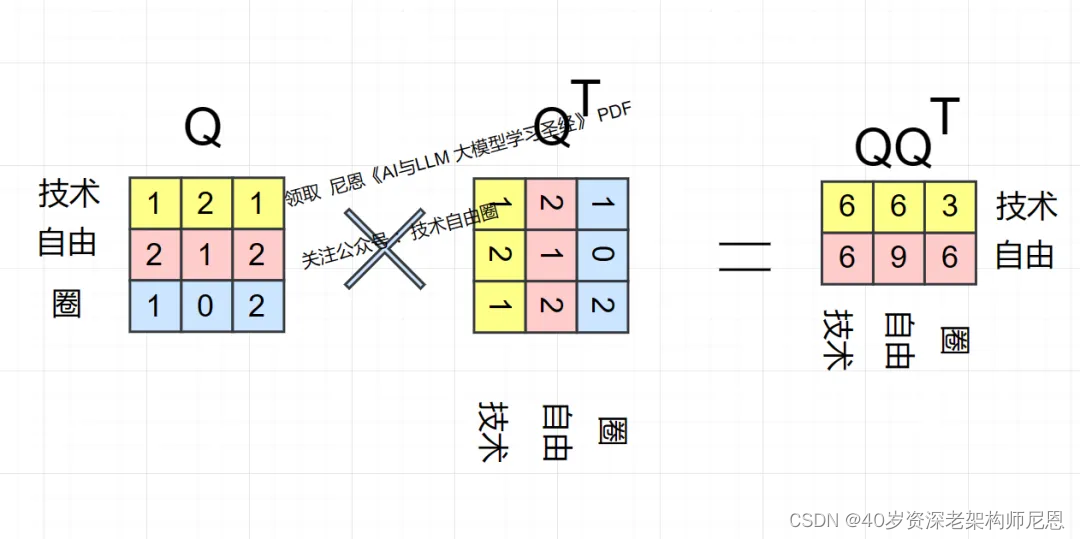
这里，非常重要的是，首先要明白的是 矩阵 与其转置相乘的含义是什么？

我们知道向量相乘的含义？

简单来说，向量相乘，表示一个向量在另一个向量上的投影。投影越大，说明向量相关性越高。

下面我们模拟一下 Q 乘以QT（Q的转置），看看具体结果的意思

首先得到的，是 技术 和 技术、技术和自由、技术和圈 ，三个分词之间的 相关性：

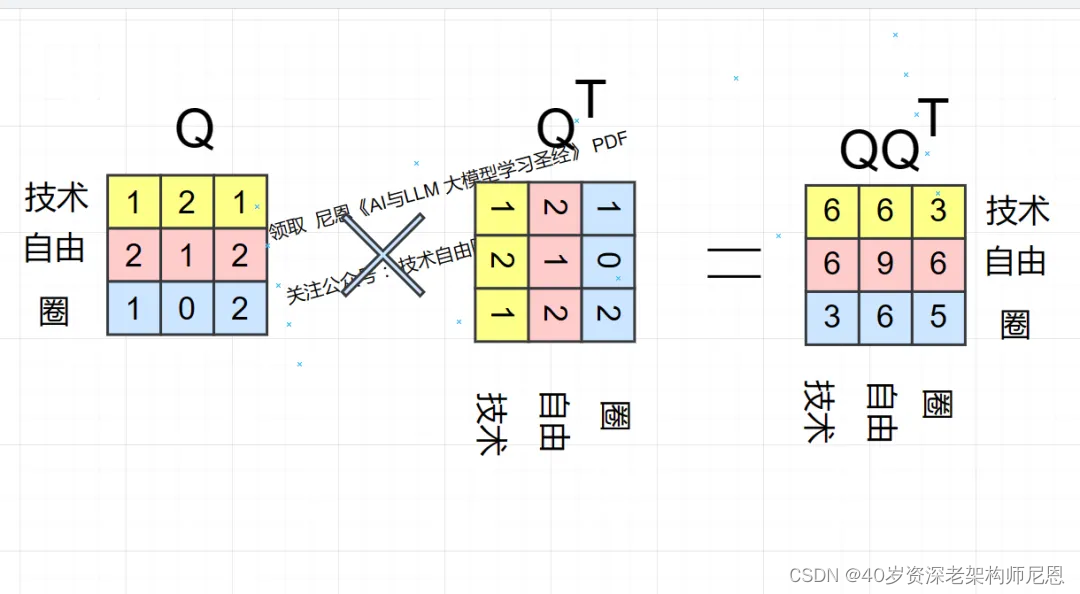
因为两个向量的内积是两个向量的相关度，那矩阵计算就是 每一纬向量和其他纬向量的相关性，

在上图中，也就是技术 和 技术、技术和自由、技术和圈 这三个分词的相关性。

第二步，计算 分词 自由 的相关性（包括自己和自己），

计算之后得到的，是 自由 和 技术、自由和自由、自由和圈 三个分词 之间的 相关性：

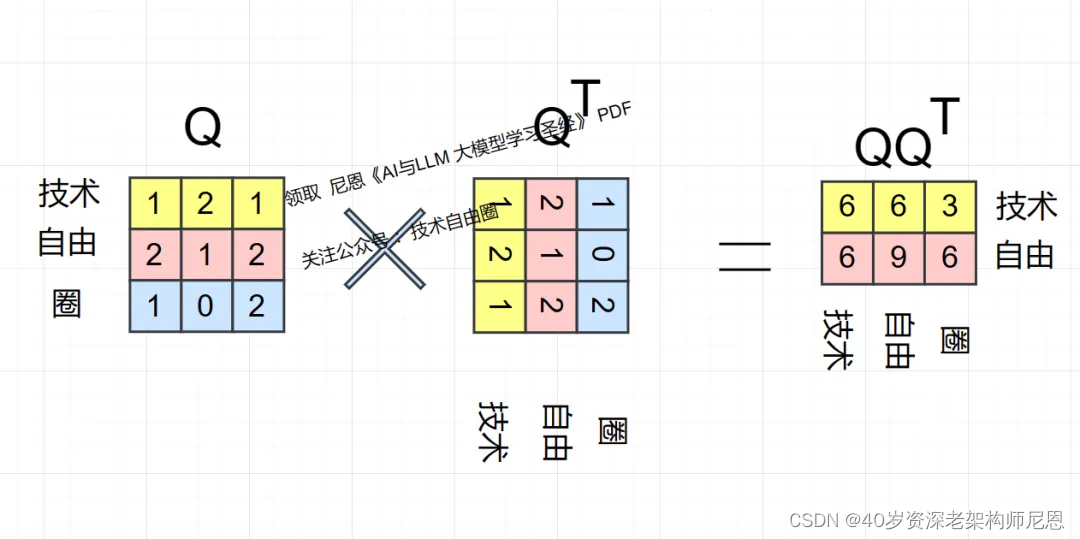
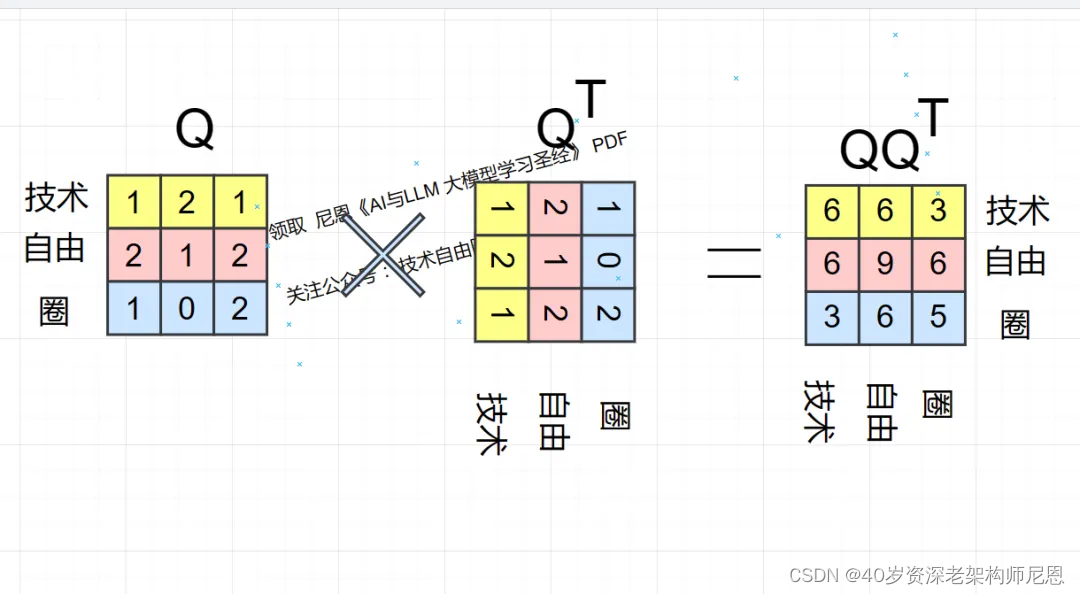
第3步，计算 分词 圈 的相关性（包括自己和自己），

最后得到的，是 圈 和 技术、圈和自由、圈和圈 三个分词之间的 相关性：

40岁老架构师尼恩提示：大模型比较难，功力浅的不容易懂。 这部分内容如果不懂，可以稍后去学习技术自由圈社群对应的配套视频《从0到1穿透LLM大模型架构》，具体请参见尼恩的公号，技术自由圈

上面的都是口算，大概率会有笔误。如果有笔误，不要怪尼恩。

尼恩的其他的 《学习圣经》《电子书》《面试宝典》《架构视频》都可能存在细节的问题， 主要是因为尼恩写的内容实在太多， 来不及细细检查，阿弥陀佛。

度量向量相似度的方法

那么，又回到了最原始的问题： 分词向量之间相关度（/相似度）表示什么？

通过上面的分析，我们大概知道：分词向量之间相关度，就是关注词A的时候，应当给予词B更多的关注，还是更少的关注。

相似度计算的方法有什么？

1、点积相似度计算

2、余弦相似度

1、点积相似度计算：

这里的点积运算可以看作是一种度量相似度的方法，它可以从数学上衡量两个向量之间的相关性。

当两个向量越相似时，它们的点积结果也会越大，那么这两个向量更应该关联在一起，也就是说键Q搜索时更应该搜索到值K。

除了点积运算，还有一种常用的度量向量相似度的方法叫做余弦相似度。

2、余弦相似度：

对于注意力机制来说，点积或者余弦相似度通常是在计算查询向量和键向量之间的相似度时使用的。

例如，在上面的公式中，a 可以表示查询向量，b 可以表示键向量。

最终的Attention 自注意力矩阵

前面算出来的，是个半成品，是个得到QKT 相似度（相关度）自注意力原生矩阵。

终于来了，需要计算最终的Attention 自注意力矩阵，

回顾 自注意力公式，也就是缩放点积注意力（Scaled Dot-Product Attention），计算的公式如下：

得到 Softmax 矩阵之后, 可以和V相乘，得到最终的输出 Attention 自注意力矩阵 Z 。

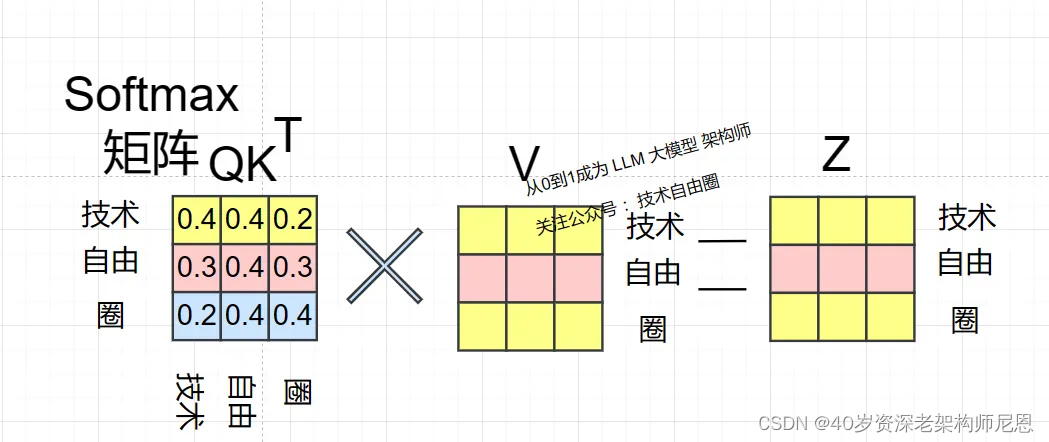
最终分词 1 的输出 Z1 等于所有分词 i 的值 Vi 根据 attention 系数的比例加在一起得到，如下图所示：

40岁老架构师尼恩提示：大模型比较难，功力浅的不容易懂。 这部分内容如果不懂，可以稍后去学习技术自由圈社群对应的配套视频《从0到1穿透LLM大模型架构》，具体请参见尼恩的公号，技术自由圈

Q、K相关度的Softmax归一化处理

得到QKT 相似度（相关度）自注意力原生矩阵之后，接下来，就需要进行Q、K之间的相关度的Softmax归一化处理，回到公式如下：

公式中计算矩阵Q和K每一行向量的内积，首先为了防止内积过大，在归一化之前，对原始的相关度值进行预处理。

这个预处理就是：通过缩放因子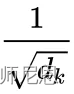
对attention为进行 scaled缩放。

40岁老架构师尼恩提示：大模型比较难，功力浅的不容易懂。 这部分内容如果不懂，可以稍后去学习技术自由圈社群对应的配套视频《从0到1穿透LLM大模型架构》，具体请参见尼恩的公号，技术自由圈

问题是，对attention为进行 scaled缩放？

完成缩放之后， 接下来，就进行 Softmax归一化处理？

什么是 Softmax归一化处理？

Softmax归一化处理通常用于分类问题中，将数据转化为概率分布。

Softmax归一化可以将原始数据映射到一个概率分布上，使得每个类别的概率值都在0到1之间，并且所有类别的概率之和为1。

这里 得到QQT 之后，使用 Softmax归一化处理， 计算每一个分词对于其他分词的 attention 系数，

公式中的 Softmax 是对矩阵的每一行进行 Softmax，即每一行的和都变为 1.

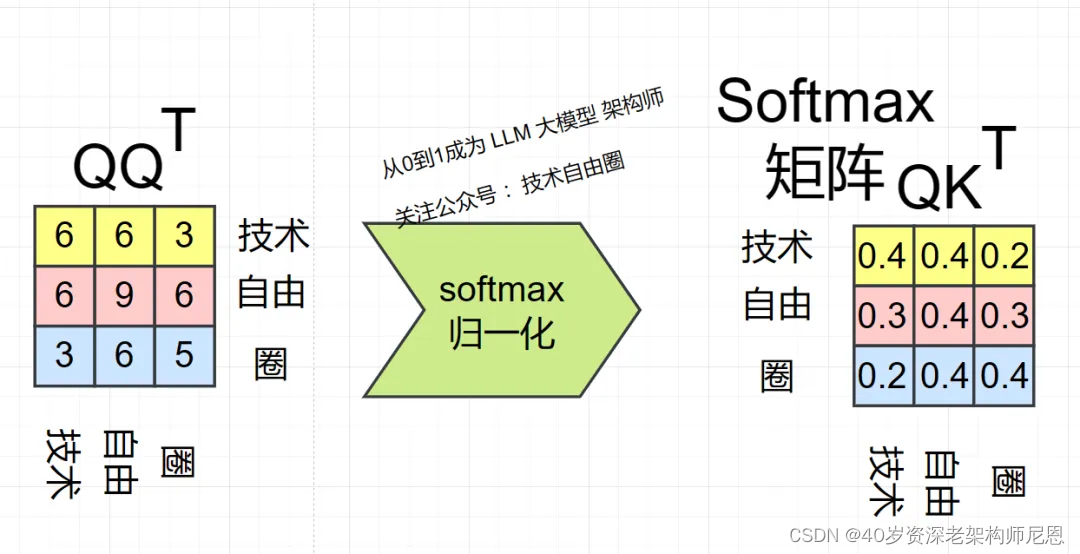
上图中 Softmax 矩阵就是 attention 系数 矩阵， attention 注意力系数矩阵 的每一行，含义如下：

• 第 1 行表示分词 1 技术 与其他所有分词的 attention 系数，
• 第 2 行表示分词 2 自由 与其他所有分词的 attention 系数，
• 第 3 行表示分词 圈 自由 与其他所有分词的 attention 系数，

到这里，我们彻底理解了线性代数里边的矩阵的相乘， 就是各个纬度的相关行计算。

之前尼恩在学习线性代数的时候，也是不知道的矩阵相差有什么用，纯粹为了学习线性代数，而去学习线性代数

感觉 大学里边学操作系统、 数据结构，都是这样。

直到尼恩在讲 第 35章netty的对象池、内存池视频的时候，才知道大学里边学习的满二叉树，原来是可以用到 内存池的 buddy算法里边， omg，大学老师，为啥不讲讲这个。

同样，如果是一个矩阵是一个user的偏好向量矩阵，

比如一个shape(5,10)维的矩阵，可以认为是这个用户有5个偏好，以及每个偏好的向量表示，向量相乘就是各个偏好的相关性。

softmax 之后，得到的数之和就是1 ，这样代表了每一个偏好权重。这就是 attention的核心 加权求和的由来。

根据上面的注意力矩阵，当关注"技术"这个字的时候，

• 应当分配0.4的注意力给它本身，
• 应当分配0.4的注意力 去关注分词 “自由”，
• 应当分配0.4的注意力 去关注分词 “圈”

这就是注意力机制

Z1 的计算方法 如下：

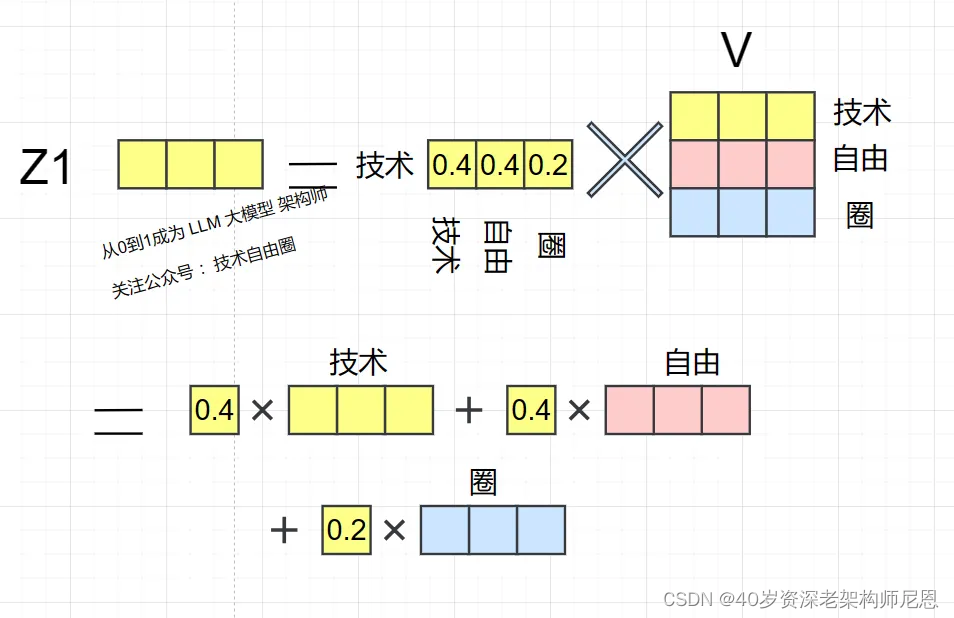
在新的向量中，每一个维度的数值都是由三个词向量在这一维度的数值加权求和得来的，

这个新的行向量就是"技术"这分词向量经过注意力机制加权求和之后的表示。

其实也可以这样理解：之前 各个纬度的向量是独立存在的，经过attenton之后，每个纬度的向量，是由其他纬共同加权求和得到的。

40岁老架构师尼恩提示：大模型比较难，功力浅的不容易懂。 这部分内容如果不懂，可以稍后去学习技术自由圈社群对应的配套视频《从0到1穿透LLM大模型架构》，具体请参见尼恩的公号，技术自由圈

注意力机制中Q和K相乘的意义是什么？为什么Q和K相乘就可以得到它们之间的相似性/权重矩阵呢？

为什么query和key相乘就能得到相似度呢？它的内部原理是什么?

在注意力机制中，query 和 key 相乘得到的相似度其实是通过计算两个向量之间的点积来实现的。

具体而言，我们将 query 和 key 进行点积运算后，再除以一个缩小因子 self.soft（一般取值为特征维度的平方根），就可以得到对应向量之间的余弦相似度，从而得到相似度分数。

补充：Softmax 的直观意思

Softmax是一种用于多分类问题的激活函数，它将模型输出的原始分数（通常称为logits）转换为表示各个类别概率的分布。直观上，Softmax函数可以被理解为一种归一化函数，它将输入的分数进行转换，使得它们都落在0到1之间，并且所有类别的概率之和为1。

例如，假设模型输出了三个类别的原始分数为[3.0, 1.0, 0.2]，Softmax函数将这些分数转换为[0.836, 0.114, 0.050]，这里每个数值代表了对应类别的预测概率。

因此，Softmax的直观意义是将模型输出的原始分数转换为概率分布，以便进行多分类问题的预测。

Transformer整体架构

回顾 Transformer 的整体结构，

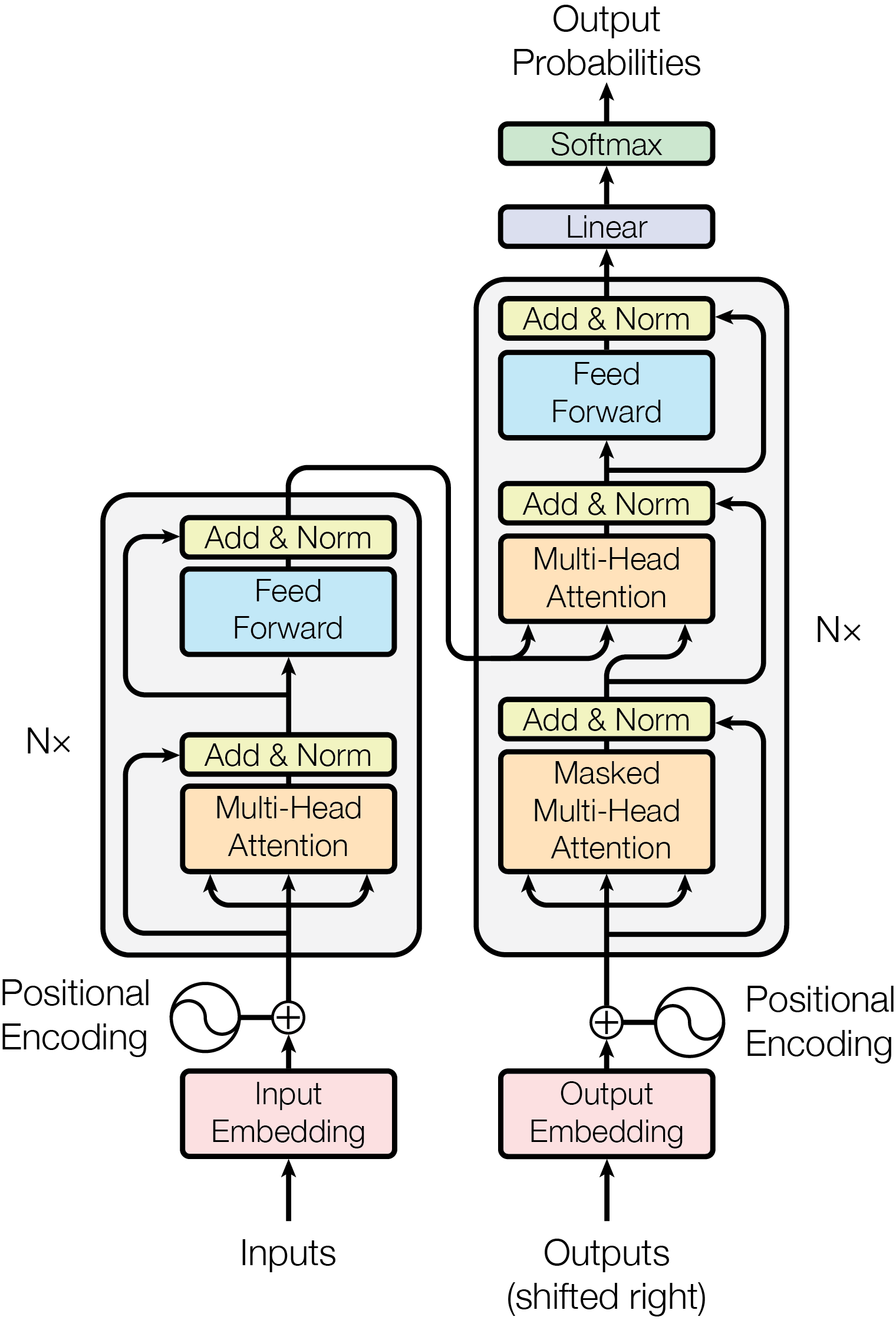
Transformer抛弃了传统的RNN和CNN，首先它使用了Attention机制，将序列中的任意两个位置之间的距离是缩小为一个常量；

其次， Transformer 不是类似RNN的顺序结构，因此具有更好的并行性，是多头注意力机制，符合现有的GPU框架，有效的解决了NLP中棘手的长期依赖问题 。

Transformer是一个encoder-decoder的结构，由若干个编码器和解码器堆叠形成。如上图

• 左侧部分为编码器，由Multi-Head Attention和一个全连接组成，用于将输入语料转化成特征向量。

• 右侧部分是解码器，其输入为编码器的输出以及已经预测的结果，由Masked Multi-Head Attention, Multi-Head Attention以及一个全连接组成，用于输出最后结果的条件概率 。

简单梳理一下，大概包括下面的几个部分：

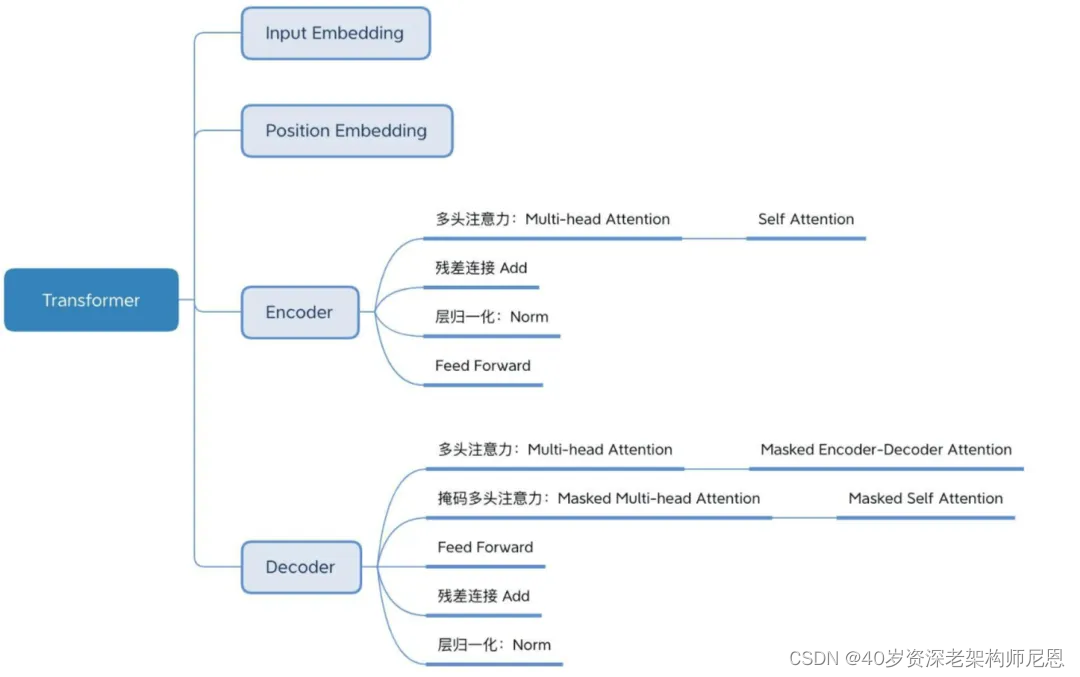
Input Embedding（输入嵌入层）

输入部分包含：

• 源文本 嵌入层及其位置编码
• 目标文本嵌入层及其位置编码

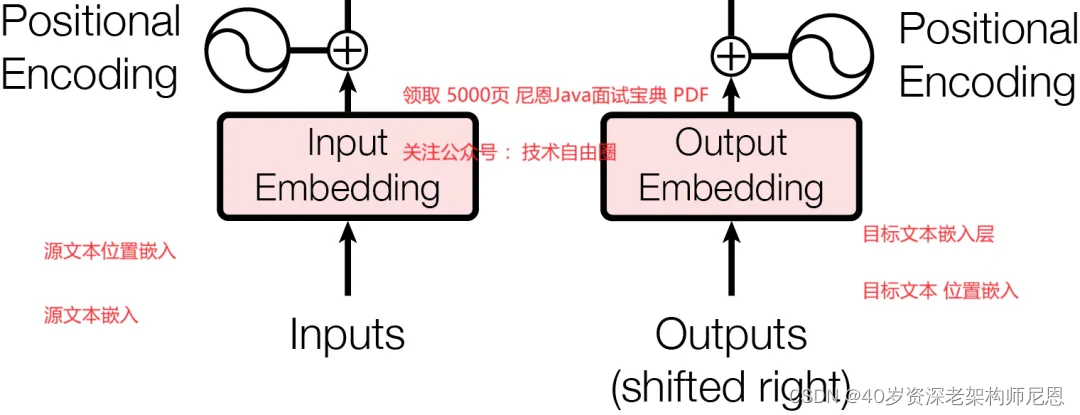
尼恩啰嗦一下，无论原文本还是目标文本，都包含两个编码向量矩阵：

• 分词的 Embedding（Embedding就是从原始数据提取出来的Feature）
• 分词位置 Embedding （位置 Feature）相加得到。

Input Embedding（输入嵌入层）要点：

• 在Transformer模型中，每时每刻的输入都是input embedding + positional encoding，即所带有的信息加上其位置编码，其中embedding就是用来取代传统RNN（如seq2seq）中的hidden states。
• 由于transformer模型属于自回归模型，因此它的下一个输出需要基于上一个输出进行推断，即主框架中的outputs（shifted right）
• position encoding是位置编码，是不可以缺失的一部分，它可以将attention计算方式无法捕捉的位置信息变成embedding形式，直接叠加到变换为embedding形式后的input中。
• 因为在解码的时候，仅知道当前词左边的部分。由此，利用masking（当前词右侧的内容被设置为−∞，这样softmax的值为0）屏蔽了当前词右边部分的影响，保持了自回归的特性。

40岁老架构师尼恩提示：大模型比较难，功力浅的不容易懂。 这部分内容如果不懂，可以稍后去学习技术自由圈社群对应的配套视频《从0到1穿透LLM大模型架构》，具体请参见尼恩的公号，技术自由圈

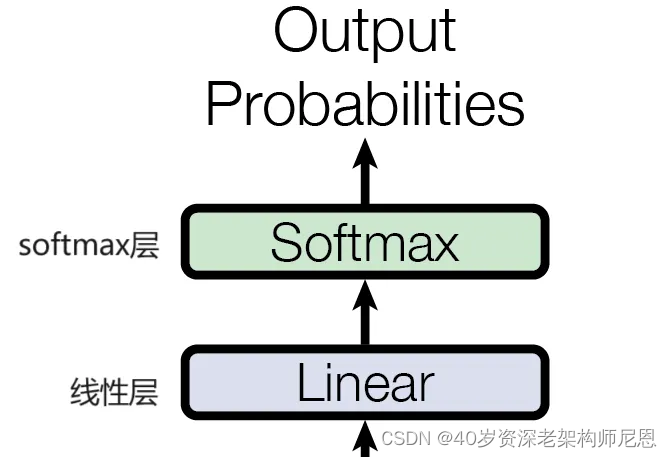
输出部分包含：

• 线性层
• softmax层

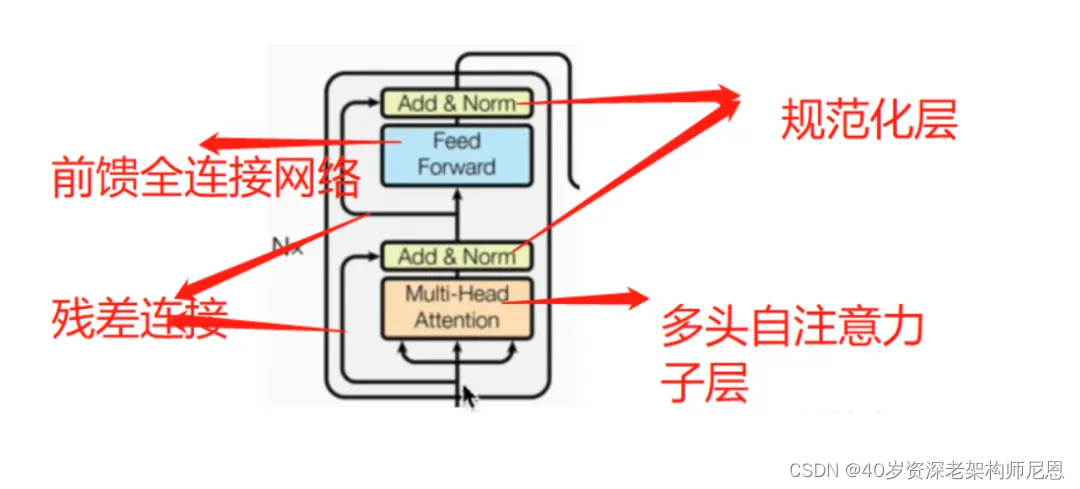
编码器部分：

• 由N个编码器层堆叠而成
• 每个编码器由两个子层连接结构组成
• 第一个子层连接结构包括一个多头自注意力子层和规范化层以及一个残差连接
• 第二个子层连接结构包括一个前馈全连接子层和规范化以及一个残差连接

40岁老架构师尼恩提示： 这部分内容如果不懂，可以稍后去学习技术自由圈社群对应的配套视频《从0到1穿透LLM大模型架构》，具体请参见尼恩的公号，技术自由圈

Multi-head Attention（多头注意）

multi-head attention由多个 scaled dot-product attention （自注意力模型）基础单元经过堆叠而成，

multi-head attention把query和key映射到高维空间的不同子空间中去计算相似度，且多头注意的输入都是query Q、key K 、value V 三个元素，只是 Q、K、V 的取值不同。

为了更好的理解multi-head attention，我们分成两步走：

第一步，回顾一下 scaled dot-product attention（缩放的点乘注意力）：

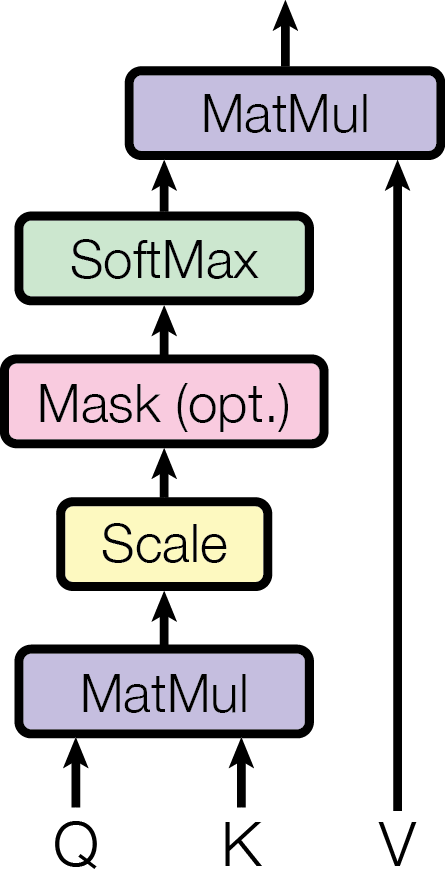
首先，attention也叫self-attention，顾名思义，就是自己和自己做attention操作，即得到所有时刻的数据后，可以用其中每一时刻数据与所有数据中任意一时刻数据进行计算attention（相似程度）。

其次，如框图所示，可以分成6步来看：

1）将编码器与文本输入生成输入向量，然后将其生成三个向量，生成方法是将输入向量分别乘以三个权重矩阵，这些矩阵是可以在训练过程学习的，而且所有的输入向量都共享这三个权重矩阵。

2）计算attention，即计算一个分值，将对应的Q、K依次进行点积获得每个位置的分值。

3）保持训练与推理的数据一致性。

4）对计算出来的分值进行softmax操作，归一化分值使得全为正数且它们的和为1。

5）将softmax分值与V的向量按位相乘，保留关注词的value值，削弱非相关词的value值。

6）将所有加权向量加起来，产生该位置的self-attention的输出结果。

第二步，介绍一下multi-head attention（多头注意）介绍：

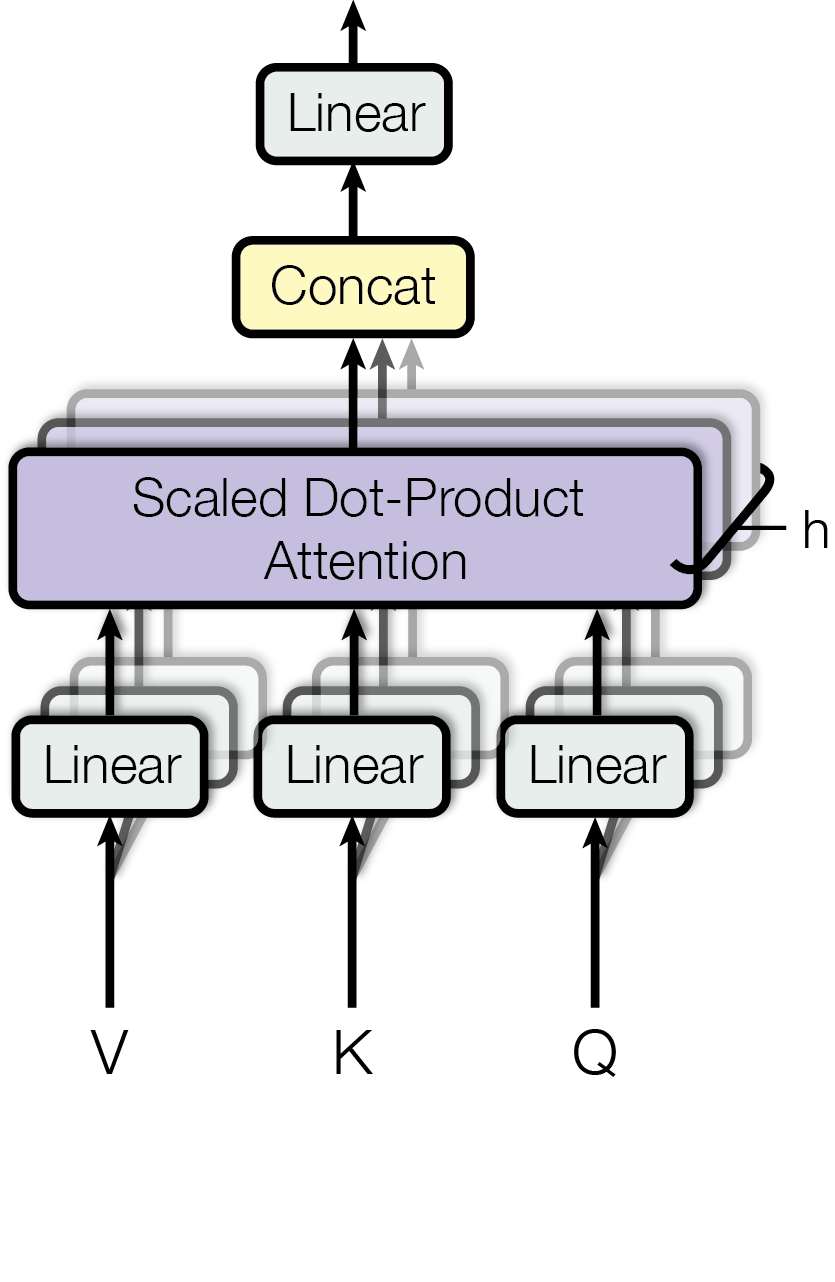
如上图所示，这就是scaled dot-product attention的堆叠（stacking），

先把我们上面讲过的Q、K、V进行线性变换变成Q’、K’、V’，然后进行attention计算，

重复这样的操作h次，然后将这h次的结果进行concat（合并），最后总的做一次线性变换，输出的就是多头注意这个模块的输出了。

而在主框架中右半部分的多头注意中，与其他两个多头注意有些差异，它是一个cross_attention，它的Q是由目标端序列而来，K、V是由源端序列来的。

40岁老架构师尼恩提示： 这部分内容如果不懂，可以稍后去学习技术自由圈社群对应的配套视频《从0到1穿透LLM大模型架构》，具体请参见尼恩的公号，技术自由圈

ADD&Normalization（残差连接与规范化层）

在 主框架 中每一个模块后面，都有一个残差连接和规范化层，

它是一个通用的技术，它的本质是可以有效的改善深层模型中梯度消失的问题，且能打破网络对称性，改善网络退化问题，加速收敛，规范化优化空间。

Feed Forward Network（FFN，前馈神经网络）

每一层经过attention之后，还会有一个FFN，这个FFN的作用就是空间变换。

FFN包含了2层linear transformation（线性变换）层，中间的激活函数是ReLu 。

FFN层就是feed forward层。他本质上就是一个MLP（Multilayer Perceptron）多层感知机。

Feed Forward前馈神经网络对应的公式如下(max相当于Relu)：

其中两层感知机中，第一层会将输入的向量升维，第二层将向量重新降维。

这样子就可以学习到更加抽象的特征。

40岁老架构师尼恩提示：大模型比较难，功力浅的不容易懂。 这部分内容如果不懂，可以稍后去学习技术自由圈社群对应的配套视频《从0到1穿透LLM大模型架构》，具体请参见尼恩的公号，技术自由圈

多头注意力（Multi-Head Attention）

多头注意力（Multi-Head Attention）和自注意力（Self-Attention）是Transformer模型中的两个关键组件，它们在注意力机制的应用上有一些区别：

1. 自注意力（Self-Attention）：
   • 自注意力机制用于计算输入序列中每个元素与其他元素的相关性。
   • 在自注意力中，输入序列中的每个元素都会与序列中的其他元素进行比较，以便更好地理解元素之间的依赖关系。
   • 自注意力机制被广泛用于处理序列数据，如自然语言处理中的句子表示和机器翻译等任务。
2. 多头注意力（Multi-Head Attention）：
   • 多头注意力是通过将多个自注意力子层的输出进行拼接来增强模型的表达能力。
   • 在多头注意力中，输入序列会经过多个并行的自注意力子层，每个子层都会学习不同的注意力表示。
   • 最终，多个注意力头的输出会被拼接起来，以丰富模型对输入序列的理解。

因此，可以说自注意力是多头注意力的基本构建单元之一。自注意力关注于序列内部的依赖关系，而多头注意力则通过整合多个自注意力头的输出来增强模型的表达能力。

**Self-Attention（自注意力机制）：**使输入序列中的每个元素能够关注并加权整个序列中的其他元素，生成新的输出表示，不依赖外部信息或历史状态。

• Self-Attention允许输入序列中的每个元素都与序列中的其他所有元素进行交互。
• 它通过计算每个元素对其他所有元素的注意力权值，然后将这些权值应用于对应元素的本身，从而得到一个加权和的输出表示。
• Self-Attention不依赖于外部信息或先前的隐藏状态，完全基于输入序列本身。

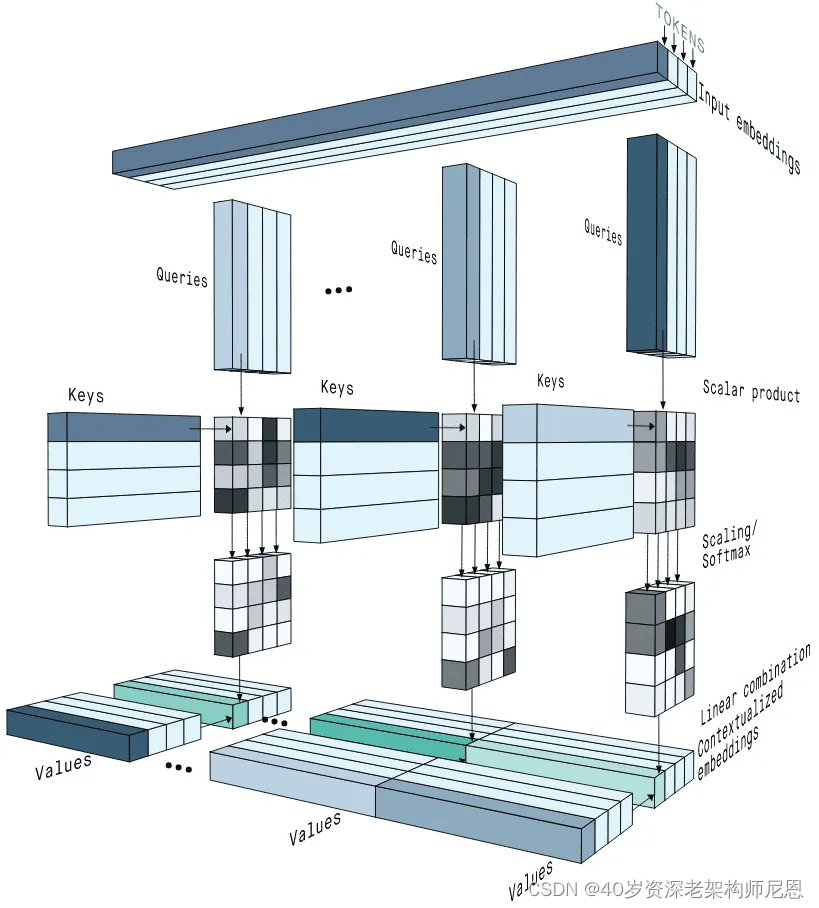
缩放点积注意力（Scaled Dot-Product Attention）是Transformer模型中的一种注意力机制，用于计算查询（query）和键（key）之间的相关性，并根据这种相关性对值（value）进行加权。在缩放点积注意力中，通过对点积结果进行缩放，以避免点积过大而导致梯度消失或梯度爆炸的问题。

具体来说，缩放点积注意力的计算过程如下：

1. 对查询（query）和键（key）进行点积运算，得到未缩放的注意力分数。
2. 将未缩放的注意力分数除以一个缩放因子（通常是查询向量的维度的平方根），以控制注意力分数的范围。
3. 将得到的缩放后的注意力分数进行softmax运算，以得到注意力权重。
4. 将注意力权重与值（value）进行加权求和，得到最终的输出。

Multi-Head Attention（多头注意力机制）：

通过并行运行多个Self-Attention层并综合其结果，能够同时捕捉输入序列在不同子空间中的信息，从而增强模型的表达能力。

• Multi-Head Attention实际上是多个并行的Self-Attention层，每个“头”都独立地学习不同的注意力权重。
• 这些“头”的输出随后被合并（通常是拼接后再通过一个线性层），以产生最终的输出表示。
• 通过这种方式，Multi-Head Attention能够同时关注来自输入序列的不同子空间的信息。

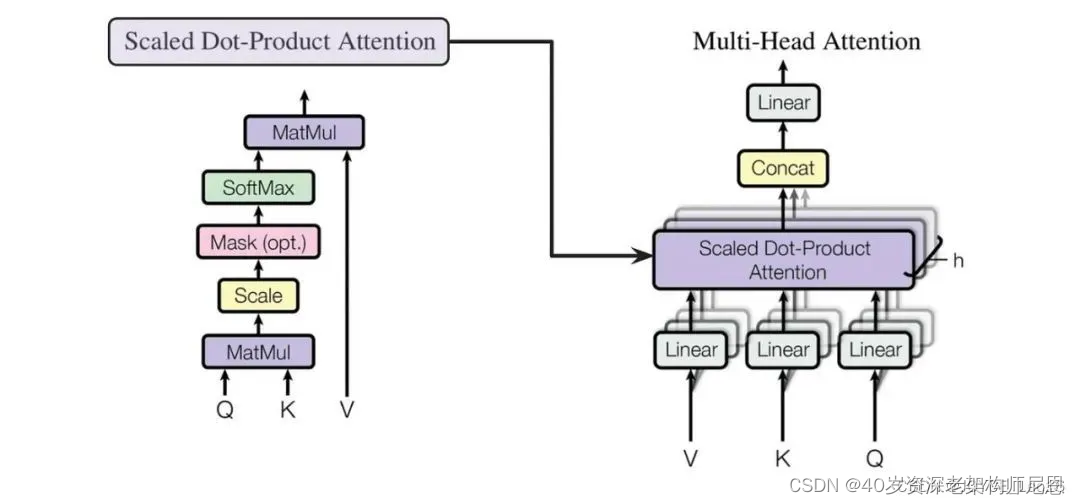
Multi-Head Attention

• **Self-Attention（自注意力机制）：**自注意力机制的核心是为输入序列中的每一个位置学习一个权重分布，这样模型就能知道在处理当前位置时，哪些位置的信息更为重要。Self-Attention特指在序列内部进行的注意力计算，即序列中的每一个位置都要和其他所有位置进行注意力权重的计算。
• **Multi-Head Attention（多头注意力机制）：**为了让模型能够同时关注来自不同位置的信息，Transformer引入了Multi-Head Attention。它的基本思想是将输入序列的表示拆分成多个子空间（头），然后在每个子空间内独立地计算注意力权重，最后将各个子空间的结果拼接起来。这样做的好处是模型可以在不同的表示子空间中捕获到不同的上下文信息。

**案例对比：**在“我爱AI”例子中，Self-Attention计算每个词与其他词的关联权重，而Multi-Head Attention则通过拆分嵌入空间并在多个子空间中并行计算这些权重，使模型能够捕获更丰富的上下文信息。

Self-Attention（自注意力机制）：

**1. 输入：**序列“我爱AI”经过嵌入层，每个词（如“我”）被映射到一个512维的向量。

2. 注意力权重计算：

​ 对于“我”这个词，Self-Attention机制会计算它与序列中其他所有词（“爱”、“A”、“I”）之间的注意力权重。

​ 这意味着，对于“我”的512维嵌入向量，我们会计算它与“爱”、“A”、“I”的嵌入向量之间的注意力得分。

**3. 输出：**根据计算出的注意力权重，对输入序列中的词向量进行加权求和，得到自注意力机制处理后的输出向量。

Multi-Head Attention（多头注意力机制）：

1. 子空间拆分：

​ 原始的512维嵌入空间被拆分成多个子空间（例如，8个头，则每个子空间64维）。

​ 对于“我”这个词，其512维嵌入向量被相应地拆分成8个64维的子向量。

2. 独立注意力权重计算：

​ 在每个64维的子空间内，独立地计算“我”与“爱”、“A”、“I”之间的注意力权重。

​ 这意味着在每个子空间中，我们都有一套独立的注意力得分来计算加权求和。

3. 结果拼接与转换：

​ 将每个子空间计算得到的注意力输出拼接起来，形成一个更大的向量（在这个例子中是8个64维向量拼接成的512维向量）。

​ 通过一个线性层，将这个拼接后的向量转换回原始的512维空间，得到Multi-Head Attention的最终输出。

Self-Attention和Multi-Head Attention通俗理解

Self-Attention（自注意力机制）

假如你在玩一堆玩具。有些玩具是朋友，它们喜欢一起玩。比如，超级英雄玩具喜欢和其他超级英雄在一起，动物玩具喜欢和其他动物在一起。当你玩一个玩具时，你会想，哪些玩具是它的好朋友？自注意力机制就像是帮助玩具找到它们的好朋友。这样，玩具们就可以更好地一起玩，让游戏更有趣。

在计算机的世界里，自注意力机制帮助电脑找出一句话里哪些词是“好朋友”，哪些词需要一起被理解。这就像帮助玩具找到它们的好朋友，让整个故事更有意思。

Multi-Head Attention（多头注意力机制）

假如你有一群不同的小朋友，每个人都有自己最喜欢的玩具。一个小朋友可能最喜欢超级英雄，另一个可能喜欢动物，还有一个可能喜欢车子。当他们一起玩时，每个人都会关注不同的玩具。然后，他们一起分享他们玩的故事，这样就可以组成一个大故事，每个玩具都有自己的角色。

多头注意力机制就像这群小朋友一样。电脑不只从一个角度看问题，而是像很多个小朋友一样，从不同的角度来看。这样，电脑就可以了解更多的事情，像小朋友们分享他们的故事一样，电脑也可以把这些不同的视角放在一起，让它更好地理解整个问题。

Multi-Head Attention 多头注意力

Multi-Head Attention（多头注意力）是深度学习中一种注意力机制，常用于Transformer等模型中。

Multi-Head Attention的直白解释如下：

1. 注意力机制：在自然语言处理和其他序列数据处理任务中，注意力机制可以帮助模型集中注意力于输入序列中的特定部分，从而更有效地进行相关性建模和信息提取。
2. 多头注意力：多头注意力是一种将注意力机制扩展到多个注意力头（也称为多个子空间）的方法。每个头都有自己的权重矩阵，它们分别学习不同的表示，并在最后的输出中被合并起来。
3. 并行计算：通过使用多头注意力，模型可以在不同的表示子空间中并行地学习相关性信息。这样可以更好地捕获输入序列的不同方面，并提高模型的表示能力和泛化能力。
4. 合并输出：在多头注意力中，每个头计算出的注意力权重矩阵和值矩阵将被组合起来，并通过线性变换进行加权和汇总，产生最终的输出。

总的来说，多头注意力允许模型同时关注输入序列中的不同方面，并通过并行计算和合并输出来提高模型的表示能力。

在上一步，我们已经知道怎么通过 Self-Attention 计算得到输出矩阵 Z，而 Multi-Head Attention 是由多个 Self-Attention 组合形成的，下图是论文中 Multi-Head Attention 的结构图。

从上图可以看到 Multi-Head Attention 包含多个 Self-Attention 层，

首先将输入X分别传递到 h 个不同的 Self-Attention 中，计算得到 h 个输出矩阵Z。

下图是 h=8 时候的情况，此时会得到 8 个输出矩阵Z。

多个 Self-Attention 并行的计算，如下图所示：

得到 8 个输出矩阵 z1 到 z8 之后，Multi-Head Attention 将它们拼接在一起 (Concat)，然后传入一个Linear层，得到 Multi-Head Attention 最终的输出Z。

Multi-Head Attention 的输出 ,如下图：

可以看到 Multi-Head Attention 输出的矩阵Z与其输入的矩阵X的维度是一样的。

40岁老架构师尼恩提示： 这部分内容如果不懂，可以稍后去学习技术自由圈社群对应的配套视频《从0到1穿透LLM大模型架构》，具体请参见尼恩的公号，技术自由圈

Add & Norm （残差连接与规范化层）

无论是Encoder 编码器结构和 decorder解码器，都有一个 Add & Norm （残差连接与规范化层） 层。

上图红色部分是 Transformer 的 Encoder block 结构，可以看到是由 Multi-Head Attention, Add & Norm, Feed Forward, Add & Norm 组成的。

刚刚已经了解了 Multi-Head Attention 的计算过程，现在了解一下 Add & Norm 和 Feed Forward 部分。

Add & Norm 层由 Add 和 Norm 两部分组成，

encoder 中，其计算公式如下：

其中 X表示 Multi-Head Attention 或者 Feed Forward 的输入，MultiHeadAttention(X) 和 FeedForward(X) 表示输出 (输出与输入 X 维度是一样的，所以可以相加)。

Add指 X+MultiHeadAttention(X)，是一种残差连接，通常用于解决多层网络训练的问题，可以让网络只关注当前差异的部分，在 ResNet 中经常用到：

40岁老架构师尼恩提示：大模型比较难，功力浅的不容易懂。 这部分内容如果不懂，可以稍后去学习技术自由圈社群对应的配套视频《从0到1穿透LLM大模型架构》，具体请参见尼恩的公号，技术自由圈

残差连接是一种在神经网络中常用的技术，特别是在深度残差网络（Residual Networks）中。其直观意思可以通过以下方式来理解：

1. 残差的含义：在神经网络中，每一层都会尝试学习输入数据的表示形式。然而，在深层网络中，由于梯度消失和梯度爆炸等问题，深层网络的训练会变得困难。残差连接的概念是建立在这个问题上的。残差是指当前层的输出与该层的输入之间的差异，即残差 = 当前层输出 - 当前层输入。
2. 直观理解：残差连接的直观意思是在神经网络中引入了一条直接连接，将当前层的输入直接加到当前层的输出上。这样做的好处在于，即使当前层无法学习到有效的特征表示，也不会完全丢失之前层学习到的信息。通过保留输入的信息，残差连接有助于缓解深层网络训练时的梯度问题，从而更容易地训练深度神经网络。
3. 优势：残差连接可以帮助提高网络的学习能力和泛化能力，因为它可以使得网络更容易地学习到恒等映射（identity mapping），即使网络深度很深。此外，残差连接还可以减少梯度消失问题，提高网络的训练速度和效率。

总之，残差连接的直观意义是通过在神经网络中引入直接连接，保留输入信息并帮助网络学习更好的特征表示，从而改善网络的训练和性能。

梯度消失和梯度爆炸 的直观意思

梯度消失和梯度爆炸是在深度神经网络训练中常见的问题，直观意思如下：

1. 梯度消失：在反向传播过程中，梯度消失指的是在深层网络中，梯度逐渐变得非常小，甚至趋近于零的现象。这意味着靠近输入层的权重更新非常小，导致网络无法有效地学习到深层特征。直观上，可以将梯度想象成是网络训练时的信号传递，梯度消失就像是信号在传播过程中逐渐衰减、消失了一样，导致后续层无法得到有效的更新和学习。
2. 梯度爆炸：与梯度消失相反，梯度爆炸是指在反向传播过程中，梯度变得非常大，甚至超过了机器数的表示范围，导致权重更新过大，网络无法稳定地收敛。直观上，可以将梯度想象成是网络训练时的能量传播，梯度爆炸就像是信号在传播过程中突然增大、失控了一样，导致网络参数的更新过大，无法得到有效的优化。

总的来说，梯度消失和梯度爆炸都是由于深度神经网络中的梯度传播过程中出现的数值问题而引起的，会影响网络的训练和性能。消除梯度消失和梯度爆炸是深度神经网络训练中的重要挑战之一。

40岁老架构师尼恩提示： 这部分内容如果不懂，可以稍后去学习技术自由圈社群对应的配套视频《从0到1穿透LLM大模型架构》，具体请参见尼恩的公号，技术自由圈

Layer Normalization（层归一化）

Norm指 Layer Normalization，通常用于 RNN 结构，Layer Normalization 会将每一层神经元的输入都转成均值方差都一样的，这样可以加快收敛。

Layer Normalization（层归一化）是一种用于神经网络中的归一化技术，旨在加速神经网络的训练和提高模型的性能。

Layer Normalization（层归一化） 直白解释如下：

1. 每层数据的标准化：Layer Normalization的核心思想是对神经网络中每一层的输入进行标准化处理。具体而言，对于每个样本，在每一层中的每个神经元的输出都会被减去该层输出的均值，并且除以该层输出的标准差。这样做的目的是让每个神经元的输出都保持在相似的尺度上，有助于加速收敛和提高模型的稳定性。
2. 独立于样本的归一化：与批量归一化（Batch Normalization）不同，Layer Normalization是针对每个样本独立进行归一化的，而不是针对整个批次。这使得Layer Normalization更适用于序列数据等不适合批量处理的情况。
3. 适用于不同大小的输入：由于Layer Normalization是针对每层的输入进行归一化的，因此它适用于不同大小的输入，不像批量归一化需要固定大小的批次。
4. 不需要学习参数：与批量归一化不同，Layer Normalization不需要学习额外的参数，因此可以减少模型的复杂度。

总的来说，Layer Normalization是一种简单而有效的归一化技术，适用于各种神经网络模型，可以提高模型的训练速度和泛化能力。

40岁老架构师尼恩提示：大模型比较难，功力浅的不容易懂。 这部分内容如果不懂，可以稍后去学习技术自由圈社群对应的配套视频《从0到1穿透LLM大模型架构》，具体请参见尼恩的公号，技术自由圈

Feed Forward前馈神经网络

1. Multi-Head Attention多头注意力，获取注意力矩阵：

   在Multi-Head Attention层中，通过多个注意力头并行地计算注意力权重，将输入序列进行加权汇总，得到一个新的表示。

   然后，对这个表示进行残差连接（Residual Connection）和层归一化（Layer Normalization），这样可以加速训练过程并减轻梯度消失问题。

2. FeedForward神经网络学习到数据中更加复杂的特征和关系，增强模型的表示能力和表达能力：

   在经过残差连接和归一化之后，数据会进入FeedForward神经网络。

在Multi-Head Attention中，主要是进行矩阵乘法，即都是线性变换，

矩阵乘法可以看作线性变换的组合。线性变换是指一个函数，它将向量空间中的向量映射到另一个向量空间中，同时保持向量加法和标量乘法的结构。在这种情况下，一个矩阵可以看作是一个线性变换的表示，而矩阵乘法则表示了对一个向量应用一系列线性变换。当我们将两个矩阵相乘时，我们实际上是将一个线性变换应用于另一个线性变换的结果。

而线性变换的学习能力不如非线性变换的学习能力强，

1. 线性变换：线性变换是指输入与权重矩阵的线性组合，不包含非线性激活函数。在神经网络中，线性变换通常是指全连接层或者简单的线性回归模型。线性变换的学习能力受限于其线性特性，无法捕捉数据中的复杂非线性关系。因此，在处理非线性数据模式时，线性变换的学习能力相对较弱。
2. 非线性变换：非线性变换引入了非线性激活函数，例如ReLU、Sigmoid、Tanh等。非线性激活函数能够引入数据的非线性特征，使神经网络能够学习和表示更复杂的数据模式和关系。非线性变换的学习能力更强，可以更好地拟合复杂的数据模式。

在实际应用中，通常会将多个线性变换和非线性变换组合起来构成深度神经网络，以提高模型的学习能力和表达能力。

Feed Forward 层通过堆叠多层非线性变换，可以学习到数据中更加复杂的特征和关系，从而实现更强大的学习能力。

Feed Forward Network（FFN，前馈神经网络）

每一层经过attention之后，还会有一个FFN，这个FFN的作用就是空间变换。

FFN包含了2层linear transformation（线性变换）层，中间的激活函数是ReLu 。

FFN层就是feed forward层。他本质上就是一个MLP（Multilayer Perceptron）多层感知机。

Feed Forward前馈神经网络对应的公式如下(max相当于Relu)：

其中两层感知机中，第一层会将输入的向量升维，第二层将向量重新降维。

这样子就可以学习到更加抽象的特征。

感知机是一种二元线性分类模型，可看作是一种简单形式的前馈神经网络，由 Frank Rosenblatt 于 1957 年提出，其输入实例的特征向量，输出实例的类别。

作为一种线性分类器，其可被看作是最简单的前向人工神经网络，尽管结构简单但依旧可以学习和处理复杂问题，其主要缺陷在于无法处理线性不可分问题。

感知机它是一种二元分类器，可将矩阵上的如 x 映射到输出值 f(x) 上。

其中，w 是实数的表示权重向量，w · x 是点积，b 是偏置常数。

f(x) 用于对 x 进行分类，以判断其是肯定的还是否定的，这属于二元分类问题，

若 b 为负值，那么加权后的输入值必须产生一个肯定值且大于 -b，这样才能令分类神经元大于阈值 0，从空间上看，偏置会改变决策边界的位置。

MLP（Multilayer Perceptron）是一种最基本的前馈神经网络结构，也称为多层感知机。

它由多个全连接层组成，每个全连接层都包含多个神经元，相邻层之间的神经元全部相连。

MLP通常由输入层、若干个隐藏层和输出层组成。输入层负责接收原始数据特征，隐藏层用于提取和转换特征，输出层则输出模型的预测结果。

MLP的基本结构如下：

• 输入层：负责接收数据的原始特征，通常是一个向量。
• 隐藏层：由若干个全连接层组成，每个全连接层都包含多个神经元。隐藏层负责对输入特征进行非线性变换和抽象，以提取更高层次的特征表示。
• 输出层：通常是一个全连接层，用于将隐藏层提取的特征映射到最终的输出空间，可以是一个标量（用于回归问题）或者一个概率分布（用于分类问题）。

MLP通过在隐藏层中引入非线性激活函数（如ReLU、Sigmoid、Tanh等），可以实现复杂的非线性建模。它在许多任务中都表现出色，包括分类、回归、聚类等。

总的来说，MLP是一种灵活、强大的神经网络结构，常用于构建各种机器学习模型，尤其是在数据特征较为复杂或者任务较为复杂时表现优异。

Feed Forward前馈神经网络对应的公式如下(max相当于Relu)：

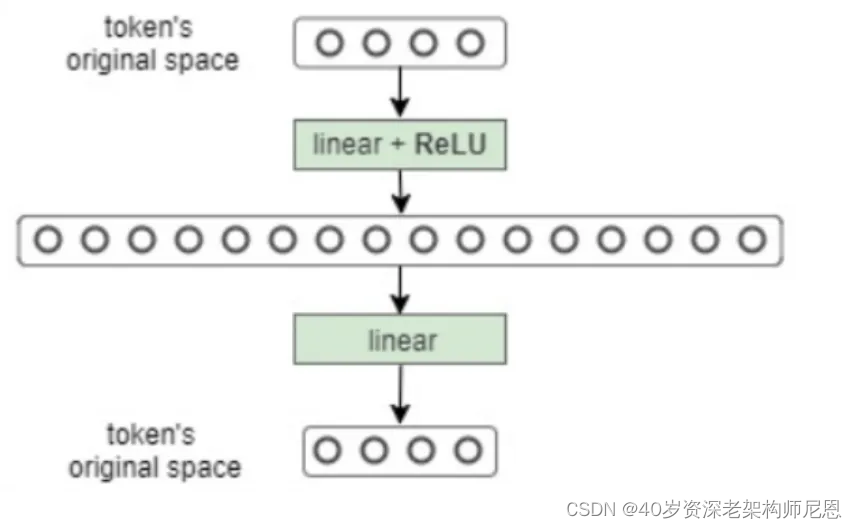
通过上图，可以看出 , Feed Forward 层比较简单，是一个两层的全连接层，

• 第一层 线性变换linear 引入了非线性激活函数Relu，注意，引入激活函数为 Relu，

• 第二层不使用激活函数

FeedForward的输入是什么呢？

X是输入，Feed Forward 最终得到的输出矩阵的维度与X一致。

X是Multi-Head Attention的输出做了残差连接和Norm之后得数据，然后FeedForward做了两次线性变换+一次非线性变换，为的是更加深入的提取特征。

所以FeedForward的作用是：通过线性变换+非线性变换结合，首先将数据映射到一个高维度的空间，然后再将其映射回一个低维度的空间，提取了更深层次的特征。

FeedForward主要的作用是在每个编码器和解码器层之间添加非线性映射,以增强模型的表达能力。

Feed Forward前馈神经网络通常由两个线性变换层组成，每个线性变换层之间会添加一个非线性激活函数（比如ReLU），以便更好地提取特征和建模非线性关系。

两个线性变换层的目的在于对特征进行更深入的提取和抽象，从而增强模型的表示能力和表达能力。

整个过程可以用如下伪代码表示：

Multi-Head Attention 输入 --> 加权汇总 --> 残差连接 --> 层归一化 --> FeedForward神经网络 --> 残差连接 --> 层归一化
1

这种结构在Transformer模型中被广泛使用，能够有效地捕获输入序列的长期依赖关系，并且具有较强的表示能力。

40岁老架构师尼恩提示：大模型比较难，功力浅的不容易懂。 这部分内容如果不懂，可以稍后去学习技术自由圈社群对应的配套视频《从0到1穿透LLM大模型架构》，具体请参见尼恩的公号，技术自由圈

Feed Forward前馈神经网络是一个全连接层。

全连接层是神经网络中最基本的层之一，也称为密集连接层（Dense Layer）或者仿射层（Affine Layer）。

在全连接层中，每个神经元都与上一层的所有神经元相连。

具体地，如果上一层有n个神经元，当前层有m个神经元，则全连接层中有n×m个连接权重，每个连接权重对应着上一层的一个神经元到当前层的一个神经元的连接。

全连接层的作用是将上一层的所有神经元的输出进行加权求和，并经过激活函数得到当前层的输出。这个加权求和过程可以看作是一个线性变换，因此全连接层具有一定的线性特性。

全连接层通常用于深度神经网络的隐藏层和输出层。在隐藏层中，全连接层可以学习到数据中的抽象特征和表示；在输出层中，全连接层可以将神经网络的输出映射到具体的预测结果或者分类概率。

全连接层的数学表达式可以表示为：

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/Li_阴宅/article/detail/848895