基于EKF扩展卡尔曼滤波的电池SOC估计算法matlab仿真_电池卡尔曼滤波

目录

1.扩展卡尔曼滤波原理

2.基于EKF的电池SOC估计

3.matlab程序

4.仿真结果

---

       基于扩展卡尔曼滤波（Extended Kalman Filter, EKF）的电池荷电状态（State of Charge, SOC）估计算法是一种在电池管理系统（Battery Management System, BMS）中广泛应用的非线性估计方法。由于电池系统通常表现出非线性的充放电特性，EKF算法通过线性化非线性系统模型，为电池SOC估计提供了一种有效的解决方案。

1.扩展卡尔曼滤波原理

       扩展卡尔曼滤波是标准卡尔曼滤波（Kalman Filter, KF）的一个扩展，用于处理非线性系统。其核心思想是在每个时间步将非线性系统近似为线性系统，从而可以应用标准卡尔曼滤波的框架。

      电池系统的状态空间模型通常可以表示为：

  

       其中，xk​ 是状态向量（通常包括SOC），uk是输入向量（如电流），yk​是观测向量（如电压），f 和h分别是非线性状态转移函数和观测函数，wk和vk​分别是过程噪声和观测噪声，通常假设为高斯白噪声。

      为了应用卡尔曼滤波，需要将非线性系统线性化。这通常通过计算雅可比矩阵来实现。

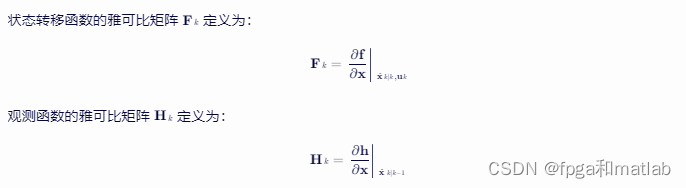
预测步骤使用前一时刻的状态估计来预测当前时刻的状态。

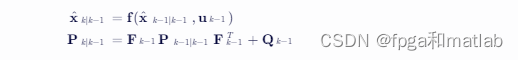
        其中，x^k∣k−1​ 是状态向量的预测值，Pk∣k−1​ 是协方差矩阵的预测值，Qk−1​ 是过程噪声的协方差矩阵。

      更新步骤使用当前时刻的观测值来修正预测值。

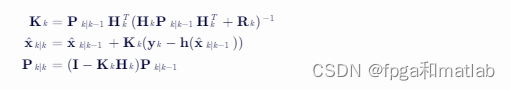
       其中，Kk​ 是卡尔曼增益，x^k∣k​ 是状态向量的更新值，Pk∣k​ 是协方差矩阵的更新值，Rk​ 是观测噪声的协方差矩阵。

2.基于EKF的电池SOC估计

        电池状态（State of Charge, SOC）是描述电池剩余电量与其总容量之比的参数，通常以百分比表示。SOC是电池管理系统（Battery Management System, BMS）中的关键状态之一，对于电动汽车、混合动力汽车以及储能系统等的性能和安全性至关重要。准确估计SOC能够帮助优化电池的使用，防止过充和过放，从而延长电池寿命。

        在电池SOC估计中，状态向量 x 通常包括SOC以及其他可能的电池参数（如内阻、极化电压等）。输入向量 u 通常是电池电流，观测向量 y 是电池端电压。电池SOC通常定义为当前剩余电量与电池总容量的比值，即：

其中，Qrem​ 表示电池当前剩余的可用电量，Qtotal​ 表示电池的总容量。

        电池SOC的估计是一个复杂的过程，因为它涉及到电池内部的化学反应、温度、老化等多种因素。在实际应用中，无法直接测量电池的SOC，而是通过测量电池的电压、电流和温度等参数，结合电池模型来估计SOC。

1.电池模型

       电池模型可以是等效电路模型（如Rint模型、Thevenin模型等），用于描述电池的动态特性。这些模型通常包括开路电压（OCV）与SOC的关系，以及其他电阻、电容元件。

2.状态方程和观测方程

       状态方程和观测方程根据所选的电池模型来确定。例如，在Thevenin模型中，状态方程可能包括SOC、极化电压等状态变量的动态变化，观测方程则是电池端电压与这些状态变量的关系。

3.初始化

       在开始滤波之前，需要对状态向量和协方差矩阵进行初始化。初始值可以根据电池的先验知识或实验数据来确定。

4.迭代过程

       在实际应用中，EKF算法通过迭代地执行预测步骤和更新步骤来估计电池的SOC。在每个时间步，根据电池的电流和电压测量值，算法会更新SOC的估计值。

3.matlab程序

................................................................
% 系统动力学部分  % 连续时间模型  
A_c = [0       0         0 ; ...
     0  (-1/(R1*C1))   0 ;... 
     0       0    (-1/(R2*C2))]; 
B_c = [(-1/Cbat); (1/C1); (1/C2)]; 
C_c = [alpha -1 -1 ];
D_c = [-R0]; 
% 创建连续时间状态空间模型
......................................................................
 
x1_hat(1) = x1(1); 
% 主循环，对每一个时间点进行迭代  
for k = 2:1:length(t)
    % 使用离散时间模型更新状态  
    x1(k) = Ad(1,1)*x1(k-1) + Bd(1,1)*I(k-1); % % 更新SOC
    x2(k) = Ad(2,2)*x2(k-1) + Bd(2,1)*I(k-1); % % 更新Vc1
    x3(k) = Ad(3,3)*x3(k-1) + Bd(3,1)*I(k-1); % % 更新Vc2
    
    % 模型预测 
    x1_hat_prev = Ad(1,1)*x1_hat(k-1) + Bd(1,1)*I(k-1);
    
    if(x1_hat_prev >1)
        x1_hat_prev = 1; 
    end 
    % 插值获取OCV斜率    
    C_ek = interp1(soc_intpts_OCV_slope', OCV_slope_intpts, x1_hat_prev);
    % 预测误差协方差  
    P_prev = A_ek*P(k-1)*A_ek'+ E_ek*Q*E_ek';
    
   % 测量更新  
   V_hat(k) = interp1(soc_intpts_OCV',OCV_intpts,x1_hat_prev) - I(k)*R0 - x2(k) - x3(k);
    % 计算卡尔曼增益 
   L = P_prev*C_ek'*inv(C_ek*P_prev*C_ek'+ F_ek*R*F_ek');
    % 更新SOC估计值 
    x1_hat(k) = x1_hat_prev + L*(V(k)-V_hat(k));
    P(k) = P_prev - L*C_ek*P_prev;% 更新误差协方差  
    
end 
figure();
hold on 
plot(t,SOC_act)
plot(t,x1_hat)
plot(t,x1)
title('扩展卡尔曼滤波器: SOC'); 
xlabel('时间'); 
ylabel('充电状态（SOC）'); 
legend('SOC 真实值','SOC 估计值','SOC OL');
up4022

4.仿真结果

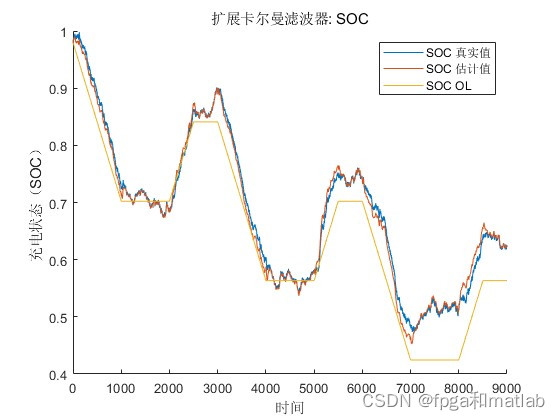
         电池SOC的估计是一个复杂而关键的任务，涉及到电池模型、状态估计技术和实时测量数据。基于模型的SOC估计方法，如扩展卡尔曼滤波，能够提供较为准确的SOC估计，但需要考虑模型的准确性和计算复杂度。在实际应用中，需要根据具体需求和条件选择合适的SOC估计方法，并结合实验数据进行验证和优化。从仿真结果可知，EKF提供了更好的SOC估计性能。从传感器偏差场景可以推断，传感器偏差建模对于更好的估计性能至关重要。此外，可以得出结论，滤波器类型及其调谐对SOC估计算法的性能都是重要的。