推荐系统（四）——因果效应uplift model系列模型S-Learner，T-Learner，X-Learner

在之前的文章中我们介绍了使用因果推断中的去除混杂和反事实的相关理论来纠正推荐系统中的偏差问题。在这篇文章中主要和大家分享uplift model相关知识和方法。

例子

小夏的商铺在上次请了明星代言后，销量有所上升，但是他不清楚是不是每个人都对这个明星感冒，有的用户可能没看到广告也打算购买。如果小夏可以给部分用户推送明星代言广告，就可以节约一些成本了（机智的小伙伴可能已经发现了，这里就是一个反事实推断的过程，即如果不展示广告会是什么样呢？）。这里就可以用uplift model来建模。

基础知识

uplift model的作用是去探究因果效应（causal effect），即上述例子中展示与不展示广告的作用有多大。但是一般而言我们是只能得到一方面的数据集，即当前状态下要么是展示了广告，要么是没展示广告。
treatment(T)：在对象上进行的干预，即do，展示与不展示广告
variable(X)：出treatment之外自带的属性特征，如年龄、性别等，这些属性多半是不受干预影响的，即无论是否展示广告，用户的性别特征都不会改变
ITE：individual treatment effect，单个用户的效应，$ITE=Y_1(x)-Y_0(x)$
ATE：average treatment effect，整体的平均效应，$ATE=E(Y_1(x)-Y_0(x))$

S-Learner

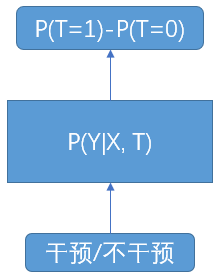
通过现有模型（LR，GBDT，NN等）对干预和不干预的数据进行训练，在预测的时候分别对该用户被干预和不被干预时的P进行预测计算，相减后便是ITE
$$ITE=E[Y|X=x,T=1]-E[Y|X=x,T=0]$$

• S-learner的优点在于他可以使用现有的模型，并且只依赖于一个模型，避免了多模型的累积误差
• 缺点在于他并没有对uplift直接建模，而是间接的做减法来得到，需要额外的特征工程

T-Learner

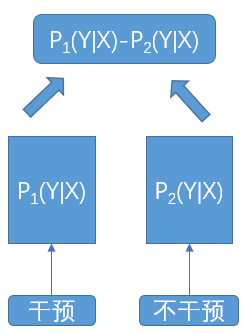
利用干预后的数据集和未干预的数据集分别训练两个模型，然后计算uplift
$$ITE=E[Y_1|X=x]-E[Y_0|X=x]$$

• 优点和S-Learner一样可以使用已有的模型，并且它不需要太多的特征工程工作
• 缺点就是存在双模型累积误差，当干预组和对照组之间的数据量差异较大，即不平衡时，对结果影响较大

X-Learner

• 通过交叉训练的方式，解决T-Learner中数据量差异问题。和T-Learner一样先用干预和不干预的数据训练两个模型分别得到${\mu }_1=E[Y_1|X=x]$和${\mu }_0=E[Y_0|X=x]$
• 用干预组的模型预测不干预的数据，用不干预的模型预测干预的数据得到$D^1=Y^1-{\mu }_0(X^1)$，$D^0={\mu }_1(X^0)-Y_0$相当于去预测被干预的人，如果不被干预购买的概率；以及未被干预的人，如果施加干预购买的概率。然后计算他们的差值作为需要拟合的数据
• 以上述D为目标，新建两个模型，${\tau }_1=E[D^1|X],{\tau }_0=E[D^0|X]$，以此拟合他们的差值。
• 通过加权得到uplift,g(x)计算权重的函数，例如可以用倾向性得分来作为函数。下式可以看一个极端情况，g(x)=1时，

$$g(x){\tau }_0+(1-g(x)){\tau }_1$$

• 优点是解决对照组和实验组之间数据不平衡的问题
• 缺点是多模型，存在误差的积累；在T-Learner的基础上还有两个模型，计算成本高
  更多内容欢迎关注“秋枫学习笔记”