NLP实践三-----特征选择_pmi点互信息算法特征选择

通过对句子的预处理，拿 中文来说，去标点，去停用词，分词后，我们可以表示出文本的特征了，当然这里还需要截取句子的长度，因为文本有长有短，机器学习需要输入相同长度的向量特征，然后基础的就是将文本向量化，比如每个单词出现的频数，这个的不足是可能有一些词出现的次数很高，但是它对文本的作用可能并没有那么大，那么这个时候可以考虑TF-IDF来降低这种影响。

TF-IDF

TF-IDF是Term Frequency - Inverse Document Frequency的缩写，即“词频-逆文本频率”。它由两部分组成，TF和IDF。
　TF就是词的频率，比如词在所有文本出现的次数，也就是之前我们说的。
　IDF就是为了降低文本出现太多的影响的作用，IDF反应了一个词在所有文本中出现的频率，如果一个词在很多的文本中出现，那么它的IDF值应该低，反过来如果一个词在比较少的文本中出现，那么它的IDF值应该高。所以定义基本公式：
　IDF(x)=logN/N(x)
当然会对它做一些平滑处理
计算过程：
下面就是这个算法的细节。

第一步，计算词频。

考虑到文章有长短之分，为了便于不同文章的比较，进行"词频"标准化。

或者

第二步，计算逆文档频率。

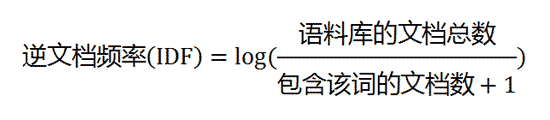
如果一个词越常见，那么分母就越大，逆文档频率就越小越接近0。分母之所以要加1，是为了避免分母为0（即所有文档都不包含该词）。log表示对得到的值取对数。
第三步，计算TF-IDF。

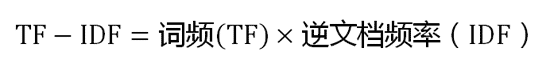
上代码：

#输入所有句子，比如预处理完的句子，返回句子的特征矩阵
def get_tf_idf_features(corpus):
    tfidf = TfidfVectorizer()
    tf_data = tfidf.fit_transform(corpus)
    df1 = pd.DataFrame(tf_data.toarray(), columns=tfidf.get_feature_names())
    return df1

# eg：
train=pd.DataFrame({'words':["I come to China to travel",
    "This is a car polupar in China",
    "I love tea and Apple ",
    "The work is to write some papers in science"]})

train=get_tf_idf_features(train['words'])
print(train)
---------------------------------
gensim训练出来的tf-idf值左边是词的id，右边是词的tfidf值
# gensim有自动去除停用词的功能，比如the
# gensim会自动去除单个字母，比如i
# gensim会去除没有被训练到的词，比如name
# 所以通过gensim并不能计算每个单词的tfidf值

from gensim import  corpora,models
# [简单分词]:
word_list = []
for i in range(len(corpus)):
    word_list.append(corpus[i].split(' '))
dictionary=corpora.Dictionary(word_list)
#输出（id,词语出现的次数）
id_times=[dictionary.doc2bow(text) for text in word_list]
print(id_times)
print(dictionary.token2id)  #查看word的id

tf_idf=models.TfidfModel(id_times)
tf_idf.save('my_idf.tfidf')  #可以保存
tf_idf.load('my_idf.tfidf')  #加载

# 使用这个训练好的模型得到单词的tfidf值
print('dddddddddddddddddddddd')
tfidf_vec = []
for i in range(len(corpus)):
    string = corpus[i]
    print(string.lower().split())
    string_bow = dictionary.doc2bow(string.lower().split())
    print(string_bow)
    string_tfidf = tf_idf[string_bow]
    print(string_tfidf)
    tfidf_vec.append(string_tfidf)
    print('ddddddddddddddddddddd')
print(tfidf_vec)



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

点互信息PMI和MI

PMI

这个指标来衡量两个事物之间的相关性大小，比如两个词。

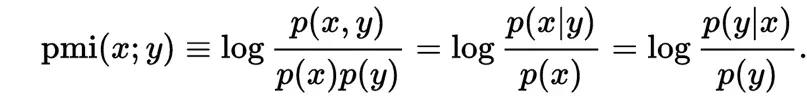
在y出现的情况下x出现的条件概率p(x|y)除以x本身出现的概率p(x)，自然就表示x跟y的相关程度，例子：

PMI(like,good)=logp(like,good)/p(like)p(good)=log p(like/good)/p(like)
p(like)是like在语料库中出现的概率（出现次数除以总词数N），p(like,good)表示like跟good在一句话中同时出现的概率（like跟good同时出现的次数除以Ngood）。PMI(like,good)越大表示like的正向情感倾向就越明显。

MI

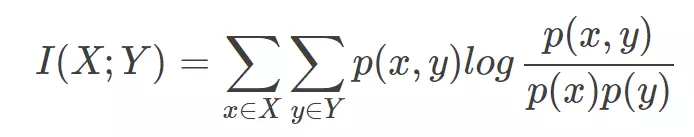
　在概率论和信息论中，两个随机变量的互信息（Mutual Information，简称MI）或转移信息（transinformation）是变量间相互依赖性的量度。不同于相关系数，互信息并不局限于实值随机变量，它更加一般且决定着联合分布 p(X,Y) 和分解的边缘分布的乘积 p(X)p(Y) 的相似程度。互信息(Mutual Information)是度量两个事件集合之间的相关性(mutual dependence)。互信息是点间互信息（PMI）的期望值。互信息最常用的单位是bit。
如果用来特征选择，这里的X就是每一个特征了，y就是标签了，通过计算所有的特征的互信息，不相关为0，相关越大MI越大，
保留相关度最大的前N个特征就好了，这是一种特征选择的方法。
但是互信息不属于度量方式，没有办法归一化，在不同数据集上的结果不好作比较，对于连续变量不敏感，而MIC就舒服多了,协方差相关系数那些不能说明非线性关系，MIC就可以，美滋滋。

MIC

最大信息系数首先寻找一种最优的离散方式，然后把互信息取值转换成一种度量方式，取值在[0,1]
上代码:

from  sklearn import metrics
from minepy import  MINE
from math import  log2,log
import numpy as np

#MI
x=np.random.uniform(-1,1,1000)
print(metrics.mutual_info_score(x,x**2))

#MIC
m=MINE()
x=np.random.uniform(-1,1,1000)
m.compute_score(x,x*x)
print(m.mic())





-------------------------------------------------------------------------------------------------
mic用于特征选择：
def mic(x, y):
    m = MINE()
    m.compute_score(x, y)
    return (m.mic(), 0.5)
 
# 选择 K 个最好的特征，返回特征选择后的数据
s=SelectKBest(lambda X, Y: tuple(map(tuple, array(list(map(lambda x: mic(x, Y), X.T))).T)), k=2).fit(x, y)
print(s.transform(x).shape)
print(s.get_support(indices=True))

result:
6.907755278982134
1.0000000000000002


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36