【图论】计算图的n-hop邻居个数，并绘制频率分布直方图

计算图的n-hop邻居个数，并绘制频率分布直方图

在图论中，n-hop邻居（或称为K-hop邻居）是指从某个顶点出发，通过最短路径（即最少的边数）可以到达的所有顶点的集合，其中n（或K）是这个最短路径的长度。换句话说，n-hop邻居就是在图中，从一个顶点出发，经过n步可以到达的所有顶点。

举个日常生活中的例子，我们的朋友是我们的1-hop邻居，我们的朋友的朋友是我们的2-hop邻居，以此类推。如果我们想找到所有与我们最多只有三层朋友关系的人（包括我们的朋友、我们的朋友的朋友、以及我们的朋友的朋友的朋友），那么这些人就是我们的3-hop邻居。

在下图中对于中间的红色节点，玫红色的就是1-hop邻居，橙色2，粉色3。

Gaudelet, T. et al. Utilizing graph machine learning within drug discovery and development. doi:10.1093/bib/bbab159.

如何在networkx中计算n-hop邻居的数量？

由定义我们可以知道，只要找到某个节点通过最短路径为n的边就可以找到它的n-hop邻居了，那么我们就可以用nx.single_source_shortest_path_length。

代码如下：

import networkx as nx
def n_hop_neighbors(G, n_hop):
    """
    Calculate n-hop neighbors for each node in the graph.
    """
    n_hop_counts = {}
    for node in G.nodes():
        # n_hop_counts[node] = len(list(nx.single_source_shortest_path_length(G, node, cutoff=n_hop))) - 1
        n_hop_counts[node] = len(list(nx.single_source_shortest_path_length(G, node, cutoff=n_hop).keys())) - 1
        
    n_hop_array = list(n_hop_counts.values())
    return n_hop_array
1
2
3
4
5
6
7
8
9
10
11
12

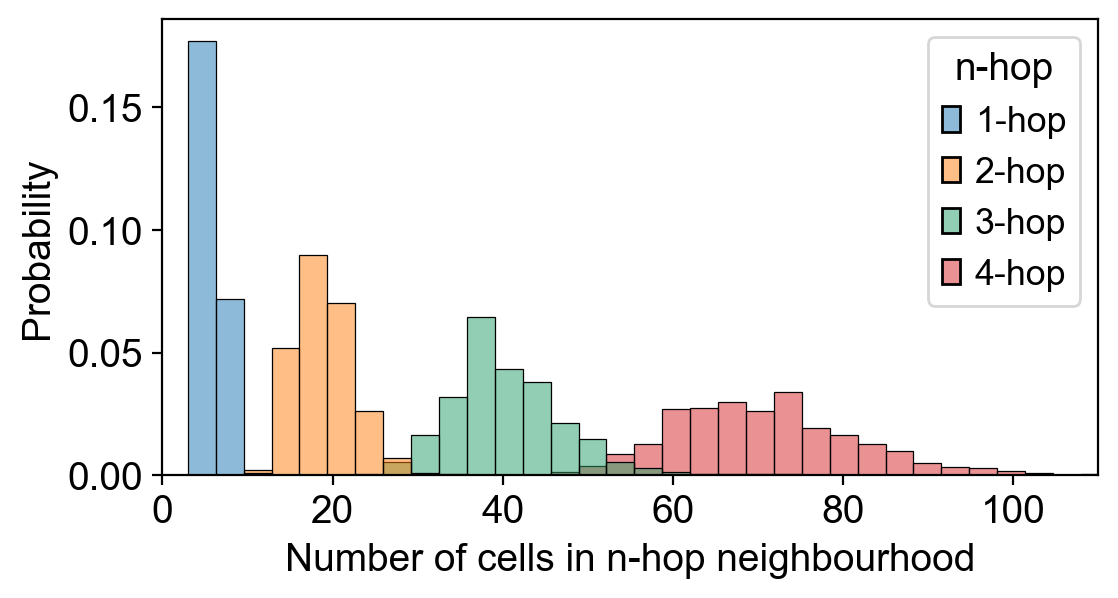
绘制分布直方图

我们使用seaborn的sns.histplot来进行绘制，代码如下：

import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Assuming G is your NetworkX graph
# Example graph
# G = nx.Graph()
# G.add_edges_from([('v1', 'v2'), ('v2', 'v4'), ('v1', 'v3')])
plt.figure(figsize=(6, 3))

# Calculate n-hop neighbors for n=1
# n_hop_counts = n_hop_neighbors(G, 3)
# Step 1: Store n-hop counts in a dictionary
n_hop_counts_dict = {}
for i in range(1, 5): # Hop counts 1 through 4
    n_hop_counts_dict[f'{i}-hop'] = n_hop_neighbors(G, i)

# Step 2: Convert the dictionary to a DataFrame
n_hop_counts_df = pd.DataFrame(n_hop_counts_dict)

# Reshape the DataFrame to long format
n_hop_counts_long = n_hop_counts_df.melt(var_name='n-hop', value_name='Number of cells in n-hop neighbourhood')
# Plotting the histogram
sns.histplot(data=n_hop_counts_long, x="Number of cells in n-hop neighbourhood", hue="n-hop", kde=False, log_scale=False, stat="probability")
plt.xlim(0, 110)
plt.grid(False)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

结果如下：