- 1香港Web3,步履蹒跚
- 208 Python之路--第七周-2--面向对象编程进阶
- 3九、回归——XGBoost算法_xgboost 回归模型
- 4291_C++_sendMsg()发送json数据给对应的URL【JSON数据交互】_c++发送json格式数据
- 5复杂网络表示的原理,算法和应用_复杂网络的表示方法
- 6探索PyTorch中的自然语言生成和NLG技术
- 7Git常用命令_git移除远程仓库链接
- 82023年全国职业院校技能大赛-信息安全管理与评估-赛题 1_计算机全国职业院校技能大赛
- 9第十五届蓝桥杯省赛第二场C/C++B组C题【传送阵】题解(AC)_15届蓝桥杯第二场研究生组
- 10latex 改变字体颜色_latex \color
数据结构与算法:排序算法_二、算法比较。设数组长度为n,插入排序的时间频度为t(n)=n*n,快速排序的时间频度
赞
踩
目录
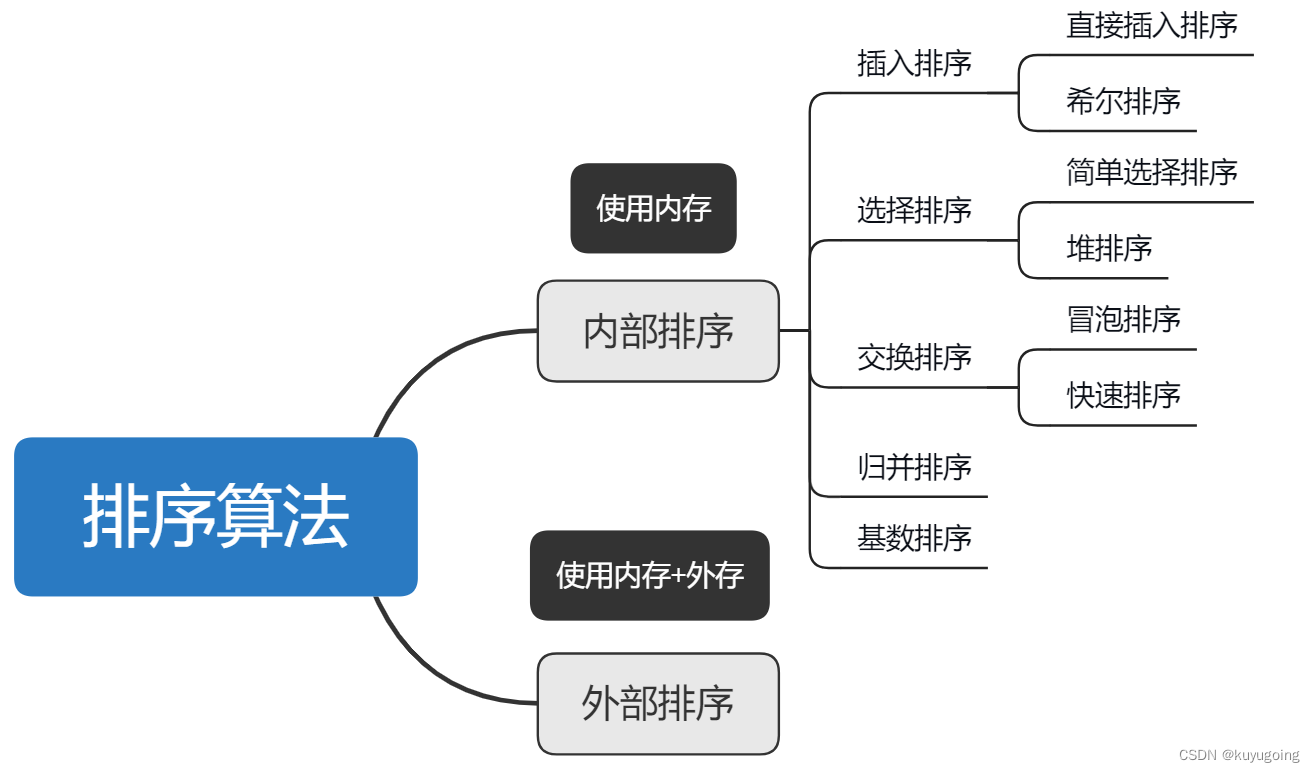
排序
排序也是一种算法
-
内部排序:指将需要处理的所有数据都加载到内部存储器中进行排序
-
外部排序:数据量过大,无法全部加载到内存中,需要借助外部存储进行排序
1、算法的时间复杂度
时间频度和时间复杂度
时间频度T(n)
一个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。
时间复杂度O(n)
一般情况下,算法中基本操作重复执行的次数是问题规模n的某个函数,用T(n)表示,若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n)) 为算法的渐进时间复杂度,简称时间复杂度。
在T(n)=4n²-2n+2中,就有f(n)=n²,使得T(n)/f(n)的极限值为4,那么O(f(n)),也就是时间复杂度为O(n²)
-
用常数1代替运行时间中的所有加法常数
-
对于不是只有常数的时间复杂度忽略时间频度的系数、低次项常数
常见的时间复杂度
-
常数阶 O(1)
int i = 1; i++;
在执行上述代码时,它消耗的时间并不随变量 i 的增长而增长,那么无论代码执行了多少行,时间复杂度都是O(1)
-
对数阶O(log2n)
while(i<n) {
i = i*2;
}
此处i并不是依次递增到n,而是每次都以倍数增长。假设循环了x次后i大于n。则2x = n,x=log2n
-
线性阶O(n)
-
线性对数阶O(nlog2n)
for(int i = 0; i<n; i++) {
j = 1;
while(j<n) {
j = j*2;
}
}
此处外部为一个循环,循环了n次。内部也是一个循环,但内部f循环的时间复杂度是log2n
所以总体的时间复杂度为线性对数阶O(nlog2n)
-
平方阶O(n²)
for(int i = 0; i<n; i++) {
for(int j = 0; j<n; j++) {
//循环体
}
}
-
立方阶O(n³)
-
k次方阶O(n^k)
-
指数阶O(2^n) 要避免使用指数阶的算法
2、排序算法的时间复杂度
| 排序算法 | 平均时间 | 最差时间 | 稳定性 | 空间复杂度 | 备注 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n^2) | O(n^2) | 稳定 | O(1) | n较小时好 |
| 交换排序 | O(n^2) | O(n^2) | 不稳定 | O(1) | n较小时好 |
| 选择排序 | O(n^2) | O(n^2) | 不稳定 | O(1) | n较小时好 |
| 插入排序 | O(n^2) | O(n^2) | 稳定 | O(1) | 大部分已有序时好 |
| 基数排序 | O(n*k) | O(n*k) | 稳定 | O(n) | 二维数组(桶)、一维数组(桶中首元素的位置) |
| 希尔排序 | O(nlogn) | O(n^s)(1<s<2) | 不稳定 | O(1) | s是所选分组 |
| 快速排序 | O(nlogn) | O(n^2) | 不稳定 | O(logn) | n较大时好 |
| 归并排序 | O(nlogn) | O(nlogn) | 稳定 | O(1) | n较大时好 |
| 堆排序 | O(nlogn) | O(nlogn) | 不稳定 | O(1) | n较大时好 |
3、冒泡排序
优化:如果在某次大循环,发现没有发生交换,则证明已经有序。所以可以添加flag标志位优化算法。
4、选择排序
算法步骤
-
遍历整个数组,找到最小(大)的元素,放到数组的起始位置。
-
再遍历剩下的数组,找到剩下元素中的最小(大)元素,放到数组的第二个位置。
-
重复以上步骤,直到排序完成。
选择排序时间会比冒泡排序短一点
5、插入排序
算法步骤
-
将待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
-
从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面)
- public class Insertion {
- public static void InsertionSort(int[] array){
- for(int cur = 1; cur < array.length; cur++){
- int tmp = cur-1;
- int val = array[cur];
- while(val < array[tmp]){
- array[tmp+1] = array[tmp];
- tmp--;
- if(tmp == -1) break; //exception
- }
- array[tmp+1] = val;
- }
- }
-
- public static void InsertionSort(int[] array, int group){
- //int num = array.length/group;
- int i = 0;
- while(i < group){
- for(int cur = i+group; cur < array.length; cur += group){
- int tmp = cur - group;
- int val = array[cur];
- while(val < array[tmp]){
- array[tmp+group] = array[tmp];
- tmp -= group;
- if(tmp == i-group) break;
- }
- array[tmp+group] = val;
- }
- i++;
- }
- }
-
- public static void ShellSort(int[] array){
- int index = array.length/2;
- while(index > 0){
- InsertionSort(array, index);
- index /=2;
- }
- }
-
- public static void showValue(int[] array){
- for(int val : array){
- System.out.print(val + " ");
- }
- System.out.println();
- }
-
-
- public static void main(String[] args) {
- int[] array = {8,9,1,7,2,3,5,4,0};
- Insertion.showValue(array);
- Insertion.ShellSort(array);
- Insertion.showValue(array);
- }
- }

6、希尔排序
回顾:插入排序存在的问题
当最后一个元素为整个数组的最小元素时,需要将前面的有序数组中的每个元素都向后移一位,这样是非常花时间的。
所以有了希尔排序来帮我们将数组从无序变为整体有序再变为有序。
算法:
将数组分组(首先分数组长度/2 ... 直到最后分为一组),每次对小规模数组用插入排序,这样可以节约值交换的时间。
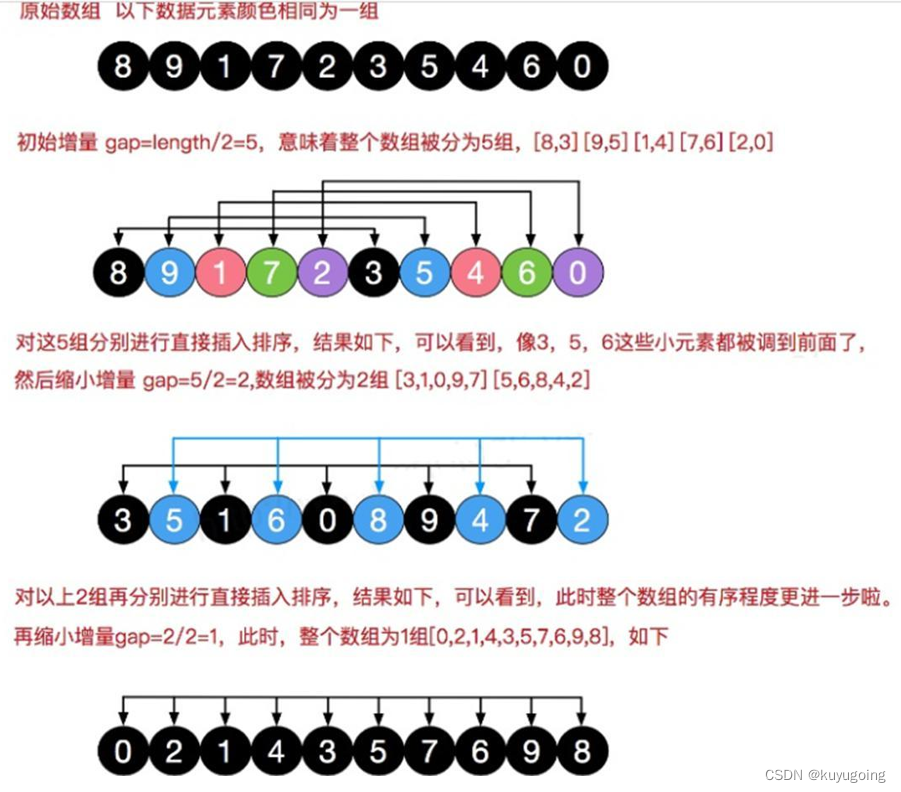
7、快速排序
算法:
-
首先在数组中选一个基准数(通常为数组第一个)
-
接着
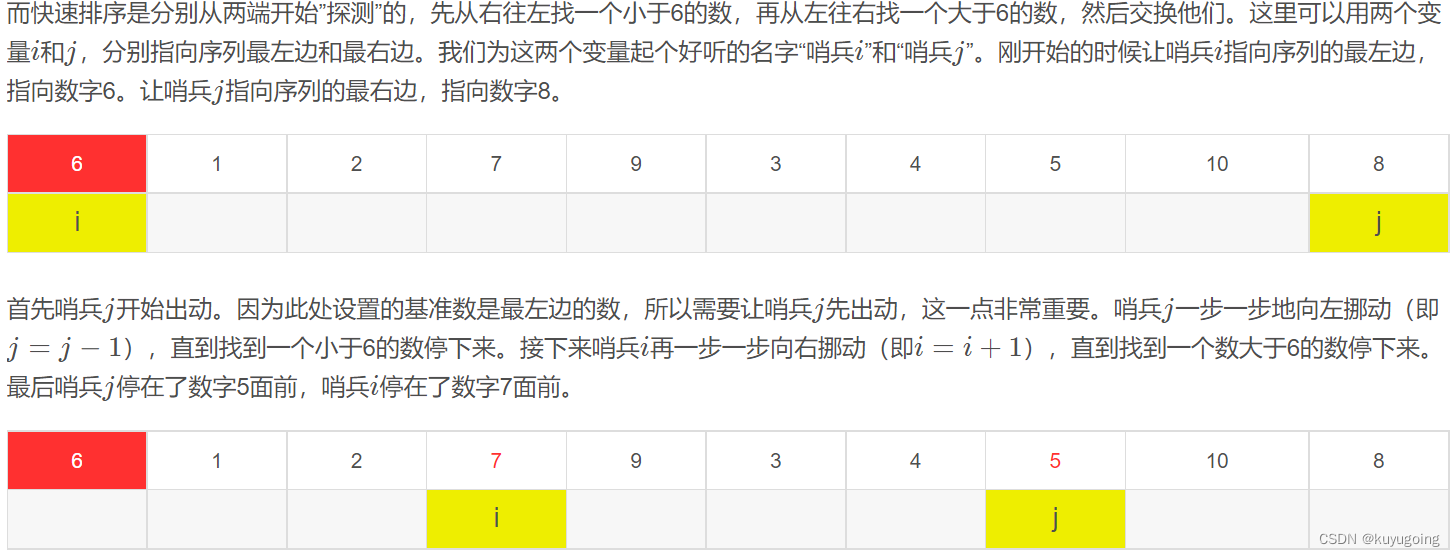
-
重复上述步骤直到 i==j ,将基准数和此位置数交换,于是得到一个左边比基准数小,右边比基准数大的数组
-
将左右两边递归直到整个数组有序
- public class quickSort {
- public static void Sort(int[] array, int aFront, int aRear){
- if(aFront >= aRear) return;
- int midValue = array[aFront];
- int front = aFront;
- int rear = aRear;
- while(front < rear){
- while(array[rear] > midValue && rear > aFront){
- rear--;
- }
- while(array[front] <= midValue && front < aRear){
- front++;
- }
- if(front < rear){
- int tmp = array[front];
- array[front] = array[rear];
- array[rear] = tmp;
- }
- }
- array[aFront] = array[rear];
- array[rear] = midValue;
- Sort(array, aFront, rear-1);
- Sort(array, rear+1, aRear);
- }
- public static void showValue(int[] array){
- for(int val : array){
- System.out.print(val + " ");
- }
- System.out.println();
- }
- public static void main(String[] args) {
- int[] array = {11,2,10,2,11};
- quickSort.showValue(array);
- quickSort.Sort(array, 0, array.length - 1);
- quickSort.showValue(array);
- }

8、归并排序
算法步骤
归并排序用到了分而治之的思想,其难点是治
-
把数组从中间划分两个子数组
-
一直递归地把子数组划分成更小的子数组,直到子数组里面只有一个元素
-
依次按照递归的返回顺序,不断地合并排好的子数组,直到最后把整个数组的顺序排好。
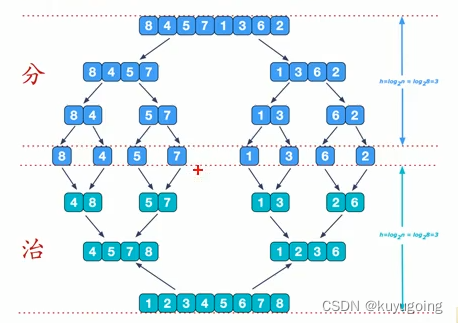
在治的阶段,输入数组左右两边的位置left right。利用一个新的数组进行排序,最后再将排序好的数组赋值给原数组。
- public class MergeSort {
-
- public static void Sort(int[] array, int left, int right){
- int mid = (right + left)/2;
- if(left < right){
- Sort(array, left, mid);
- Sort(array, mid+1, right);
- Merge(array, left, right);
- }
- }
-
- public static void Merge(int[] array, int left, int right){
- int mid = (right + left)/2;
- int pointer1 = left;
- int pointer2 = mid + 1;
- int[] tmp = new int[right - left + 1];
- int index = 0;
-
- while(pointer1 <= mid && pointer2 <= right){
- if(array[pointer1] < array[pointer2]){
- tmp[index] = array[pointer1];
- index++;
- pointer1++;
- }else{
- tmp[index] = array[pointer2];
- index++;
- pointer2++;
- }
- }
-
- if(pointer1 <= mid){
- while(pointer1 <= mid){
- tmp[index] = array[pointer1];
- index++;
- pointer1++;
- }
- }else{
- while(pointer2 <= right){
- tmp[index] = array[pointer2];
- index++;
- pointer2++;
- }
- }
-
- for(int i=0; i <= right - left; i++){
- array[left + i] = tmp[i];
- }
- }
-
- public static void showValue(int[] array){
- for(int val : array){
- System.out.print(val + " ");
- }
- System.out.println();
- }
-
- public static void main(String[] args) {
- int[] array = {4,1,4,2,2,3,8,9,11,10,5,6,7,1};
- Sort(array, 0, array.length-1);
- showValue(array);
- }

9、基数排序
基本思想:将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成了一个有序序列。


