每周一算法：双端队列广搜

题目链接

电路维修

题目描述

达达是来自异世界的魔女，她在漫无目的地四处漂流的时候，遇到了善良的少女翰翰，从而被收留在地球上。翰翰的家里有一辆飞行车。有一天飞行车的电路板突然出现了故障，导致无法启动。

电路板的整体结构是一个$R$行$C$列的网格（$R,C\le 500$），如下图所示：

每个格点都是电线的接点，每个格子都包含一个电子元件。电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。在旋转之后，它就可以连接另一条对角线的两个接点。电路板左上角的接点接入直流电源，右下角的接点接入飞行车的发动装置。

达达发现因为某些元件的方向不小心发生了改变，电路板可能处于断路的状态。她准备通过计算，旋转最少数量的元件，使电源与发动装置通过若干条短缆相连。不过，电路的规模实在是太大了，达达并不擅长编程，希望你能够帮她解决这个问题。

注意：只能走斜向的线段，水平和竖直线段不能走。

输入描述

输入文件包含多组测试数据。

第一行包含一个整数$T$，表示测试数据的数目。对于每组测试数据，第一行包含正整数$R$和$C$，表示电路板的行数和列数。

之后$R$行，每行$C$个字符，字符是/和\中的一个，表示标准件的方向。

输出描述

对于每组测试数据，在单独的一行输出一个正整数，表示所需的缩小旋转次数。
如果无论怎样都不能使得电源和发动机之间连通，输出NO SOLUTION。

样例输入

1
3 5
\\/\\
\\///
/\\\\
1
2
3
4
5

样例输出

1
1

算法思想

根据题目描述，每个格子都包含一个电子元件，主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆，如下图所示。

旋转一个电子元件的代价为$1$，问最少旋转几个元件，使起点与终点通过若干条短缆相连。

连通性

由于只能走斜向的线段，水平和竖直线段不能走，所以选择左上角的接点作为起点，只能连接如下图（左）绿色的接点，二下图（右）红色的接点是无法连通的。

通过分析发现，如果将起点设为左上角，那么能够连接的点（绿色），其行列值的和为偶数。因此，是否使得电源和发动机之间连通，需要判断$(n+m)$是否为偶数。

最小代价

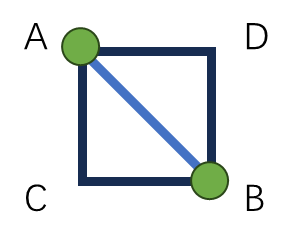
如果电子元件的最初状态为下图所示，那么从$A->B$的代价为$0$，不需要旋转；而从$C->D$的代价为$1$，需要旋转$1$次。

因此，求旋转最少数量的元件，使电源与发动装置通过若干条短缆相连，可以转换为求从起点到终点，当连接的两点之间代价为$0$或$1$时的最短路。

双端队列广搜

对于只包含边权$0$和$1$的最短路问题，可以使用双端队列广搜求解。与普通的BFS不同的是：

• 如果扩展到的新节点边权为$0$时，需要把新节点插入队列的头部。

这样处理满足BFS的两个性质：

• 两段性：队列中同时存在的所有点到起点的距离差值最多是1。
• 单调性：队列分成两段，前面一定是小的

因此可以使用BFS求最短路。

代码实现

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;

typedef pair<int, int> PII;
const int N = 505;
char g[N][N];
int n, m, st[N][N], dis[N][N];
 //元件的偏移值:左上，右上，右下，左下
int dx[4] = {-1, -1, 1, 1}, dy[4] = {-1, 1, 1, -1};
//连接元件的电缆方向在字符数组位置的偏移值:左上，右上，右下，左下
int ix[4] = {-1, -1, 0, 0}, iy[4] = {-1, 0, 0, -1};
//不需要旋转的连接方向，左上，右上，右下，左下
char c[] = "\\/\\/"; //"\/\/"
int bfs()
{
    memset(st, 0, sizeof st);
    memset(dis, 0x3f, sizeof dis);
    deque<PII> q;
    dis[0][0] = 0; q.push_back({0, 0});
    while(q.size())
    {
        PII t = q.front(); 
        q.pop_front(); //从队头出队
        int x = t.first, y = t.second;
        if(st[x][y]) continue;
        st[x][y] = true;
        for(int i = 0; i < 4; i ++)
        {
            //扩展到的元件左上角的行列值
            int a = x + dx[i], b = y + dy[i]; 
            if(a < 0 || a > n || b < 0 || b > m) continue;
            int ai = x + ix[i], bi = y + iy[i];//元件方向在数组中的位置
            int w = g[ai][bi] != c[i]; //如果不是正确的连接方向，需要旋转，边权为1
            if(dis[a][b] > dis[x][y] + w)
            {
                dis[a][b] = dis[x][y] + w;
                if(w == 1) q.push_back({a, b}); //边权为1加入队尾
                else q.push_front({a, b}); //边权为0加入队头
            }
        }
        
    }
    return dis[n][m];
}
int main()
{
    int T;
    cin >> T;
    while(T --)
    {
        cin >> n >> m;
        for(int i = 0; i < n; i ++) cin >> g[i];
        if(n + m & 1) {
            puts("NO SOLUTION");
            continue;
        }
        int t = bfs();
        if(t == 0x3f3f3f3f) puts("NO SOLUTION");
        else cout << t << '\n';
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63