LSTM架构详解

LSTM 是深度学习中很常见也很有用的一种算法，特别是在自然语言处理中更是经常用到，那么 LSTM 架构中的内部结构又是什么样子的呢？首先我们来看 LSTM 的整体框架:

在这幅图中，中间是一个 LSTM 模块，有三个输入分别是：$c^{t-1}$、$h^{t-1}$ 和 $x^t$，然后经过 LSTM 之后，输出分别是 $c^t$、$h^t$ 和 $y^t$，其中 $x^t$ 表示本轮的输入，$h^{t-1}$ 表示上一轮的状态量输出，$c^{t-1}$ 表示上一轮全局一个信息的载体；然后 $y^t$ 表示本轮的输出，$h^t$ 表示本轮的状态量输出，$c^t$ 表示本轮全局的一个信息载体。这么看来 LSTM 的一个大体框架就明白了。LSTM 的内部构造是什么样子的呢？
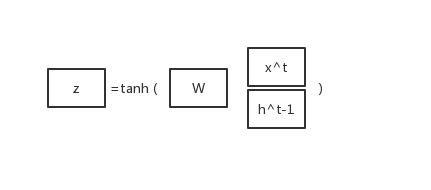
首先，我们将 $x^t$ 和 $h^{t-1}$ 合并成一个向量再乘以一个向量 $W$，外面再包一层 $tanh$ 函数，得到一个向量 $z$：

同样的道理，我们将 $x^t$ 和 $h^{t-1}$ 合并成一个向量，但是我们的激活函数用的是 $sigmoid$，示意图如下所示：

再分别乘以矩阵 $W^f$ 、$W^i$ 和 $W^o$ 得到 $z^f$、$z^i$ 和 $z^o$，然后我们可以用这些向量来由 $c^{t-1}$ 求得 $c^t$，公式是：
$$c^t=z^f\cdot c^{t-1}+z^i\cdot z$$
然后得到 $c^t$ 之后，我们可以得到 $h^t$，公式是：
$$h^t=z^o\cdot \tanh (c^t)$$
最后我们可以得到本轮的输出 $y^t$，公式是：
$$y^t=\sigma (W^{\prime }{h}^t)$$
综上所述，我们可以得到一个完整的 LSTM 的内部结构如下图所示：

有了这个结构图，我们就能够清晰直观地看出 LSTM 的内部结构，首先绿色的部分表示本轮的输入 $x^t$ 和输出 $y^t$；蓝色的部分表示上一轮的状态量 $h^{t-1}$ 和本轮输出的状态量 $h^t$；红色的部分表示上一轮的信息载体 $c^{t-1}$ 和本轮输出的信息载体 $c^t$。这是单个 LSTM 单元，我们可以将多个的 LSTM 单元级联起来就可以成为我们的 LSTM 深度学习网络，示意图如下所示:

好了，看完 LSTM 的整体架构之后，我们再来分析一下具体的每一个部分。整个LSTM 架构之所以能够记忆长期的信息，主要有 $c^n$ 这个状态，我们可以看到 $c^{t-1}$ 到 $c^t$ 中间只有少量的信息交互，所以能够保持整个网络的信息在 LSTM 间传递，如下是 $c^t$ 的状态示意图：

LSTM 之所以能够记忆长短期的信息，是因为它有 “门” 的结构来去除和增加信息到神经元的能力，“门” 是一种让信息选择性通过的方法。
首先就是遗忘门，在 LSTM 中的第一步是决定我们需要从神经元状态中遗忘哪些信息。如下图所示，两个输入通过一个 $sigmoid$ 函数，所以输出的值在 $0-1$ 之间，1表示信息完全保留，0表示信息完全遗忘。通过遗忘门，LSTM 可以选择性遗忘一些无意义的信息。如下图方框内的内容所示，这个部分就是 LSTM 中的遗忘门：

这个部分可以用公式表示成：
$$z^f=\sigma (W_f\cdot [h_{t-1},x_t]+b_f)$$
然后下一步我们需要确认什么样的新信息存放在神经元的状态中，这个部分有两输入，一个 $sigmoid$ 层决定什么值 LSTM 需要更新，一个 $tanh$ 层创建一个新的候选值向量，这个值会被加入到状态当中，然后我们需要将这两个信息来产生对状态的更新，叫做输入门，过程如下示意图：

整个的过程可以用公式表示为：

$$z^i=\sigma (W_i\cdot [h_{t-1},x_t]+b_i)$$
$$z=\tanh (W\cdot [h_{t-1},x_t]+b)$$
确定了需要更新的信息之后，我们就可以更新 $c^t$ 这个变量，在之前的图中有表示过 $c^{t-1}$ 到 $c^t$ 的过程，用公式可以表示成：
$$c^t=z^f\cdot c^{t-1}+z^i\cdot z$$
在这个过程中，$z^f\cdot c^{t-1}$ 表示之前的状态信息 $c^{t-1}$ 遗忘掉部分需要丢弃的信息，然后加上 LSTM 系统新的候选值向量，就是系统新一轮的信息 $c^t$。
说完了更新的信息状态，我们同时也要更新系统的神经元状态 $h^t$，整个过程入下图框中所示：

这就是控制 LSTM 输出的输出门，系统需要确定输出什么值。这个输出也会基于当前神经元的状态，首先我们用一个 $sigmoid$ 来确定神经元需要将哪些部分进行输出，接着，我们将 LSTM 系统的信息通过一个 $tanh$ 函数进行处理，最后将他们进行相乘输出，就是 LSTM 新的状态量。这个部分加上一个 $sigmoid$ 就是这一轮的输出 $y^t$。用公式可以写成：
$$z^o=\sigma (W_o\cdot [h_{t-1},x_t]+b_o)$$
$$h_t=z_o\cdot \tanh (c^t)$$
$$y_t=sigmoid(W^{\prime }\cdot h_t)$$
所以整个的 LSTM 可以分成如上所述的这些部分，每一个部分都有着不同的作用，希望这篇博文能够帮助您透彻理解 LSTM 神经网络的结构以及原理。文中如有纰漏，欢迎大家不吝指教；如有转载，也请标明出处，谢谢。