2024五一杯数学建模B题思路分析 - 未来新城背景下的交通需求规划与可达率问题

1 赛题

B题 未来新城背景下的交通需求规划与可达率问题
随着城市化的持续发展，交通规划在新兴城市建设中显得尤为关键。在未来新城规划中，自动驾驶技术预期将成为交通出行的主导模式，彻底改变出行方式和城市规划的基础理念。自动驾驶车辆，得益于先进的传感器、智能算法和通信技术，能够自动遵循预设路线，无需人为操作。将自动驾驶技术整合到一个特定未来新城的交通需求规划中，以期实现更高效、更可持续的城市交通网络。

交通需求指从特定起点出发，到达指定终点的交通量(车辆数)。以图1中的交通网络1为例，假设(起点,终点)对(1,4)的交通需求为100辆，其中40辆分配到路径1-2-4，60辆车分配到路径1-3-4，该过程称为交通需求分配。在道路完全通畅的情况下，从起点1到达终点4的交通量比例(以下称为“可达率”)为(40+60)/100=100%。而一旦产生突发状况，例如路段1-2发生了交通事故导致该路段无法通行，那么原本选择通过1-2-4路径的交通需求将无法满足。此时，只有通过路径1-3-4的交通需求才能够被实现，交通需求可达率为60/100=60%。

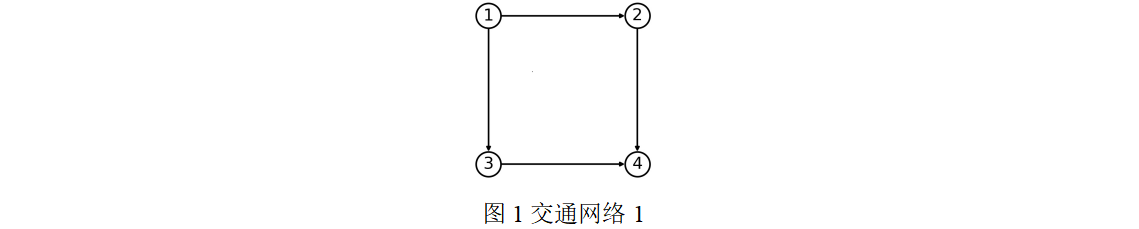
假设每个(起点,终点)对之间使用的路径数不超过5(各路段长度均为单位1，优先选择距离短的路径)。假设交通网络中所有车辆均为无人驾驶车辆，并且所有车辆都服从系统预先规划的路径进行出行。注意：本题的图2和图3中的路段为双向路段，即路段2-3和路段3-2是两条不同的路段。在本题中，不要求交通流量值取整数，即交通流量值可以为任意的非负实数。请依据附件1~3，建立数学模型，完成以下问题：
问题1：图2为一个小型交通网络。各(起点,终点)对之间的交通需求见附件1。请建立数学模型，给出各(起点,终点)对之间交通需求分配到对应路径上的交通量，使得网络中任意1条路段出现突发状况时(每个路段出现突发状况概率相同)，网络中所有交通需求的期望可达率最大。在表1中填入指定(起点,终点)对规划的路径，以及对应分配的交通量(若规划路径数不足5条无需填满表格)。


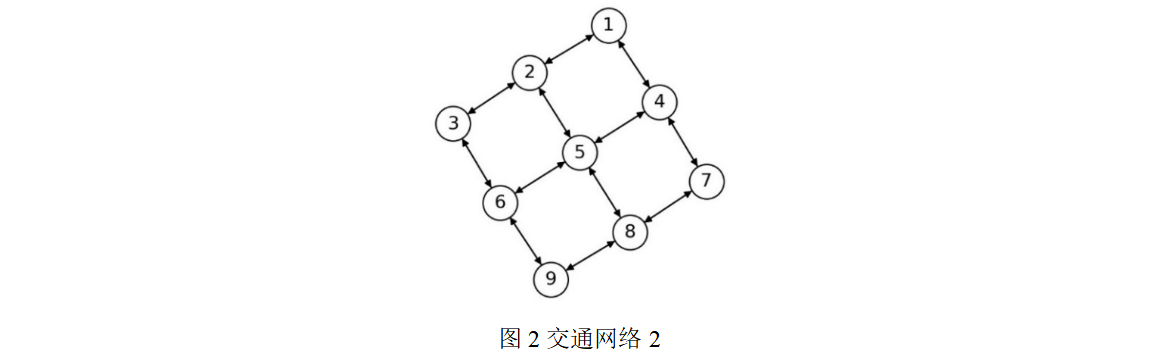
问题2：在图3所示的交通网络中，各(起点,终点)对之间的交通需求见附件2。请建立数学模型，给出各(起点,终点)对之间交通需求分配到对应路径上的交通量，使得网络中任意5条路段出现突发状况时(每个路段出现突发状况概率相同)，网络中所有交通需求的期望可达率最大。在表2中填入指定(起点,终点)对规划的路径，以及对应分配的交通量(若规划路径数不足5条无需填满表格)。


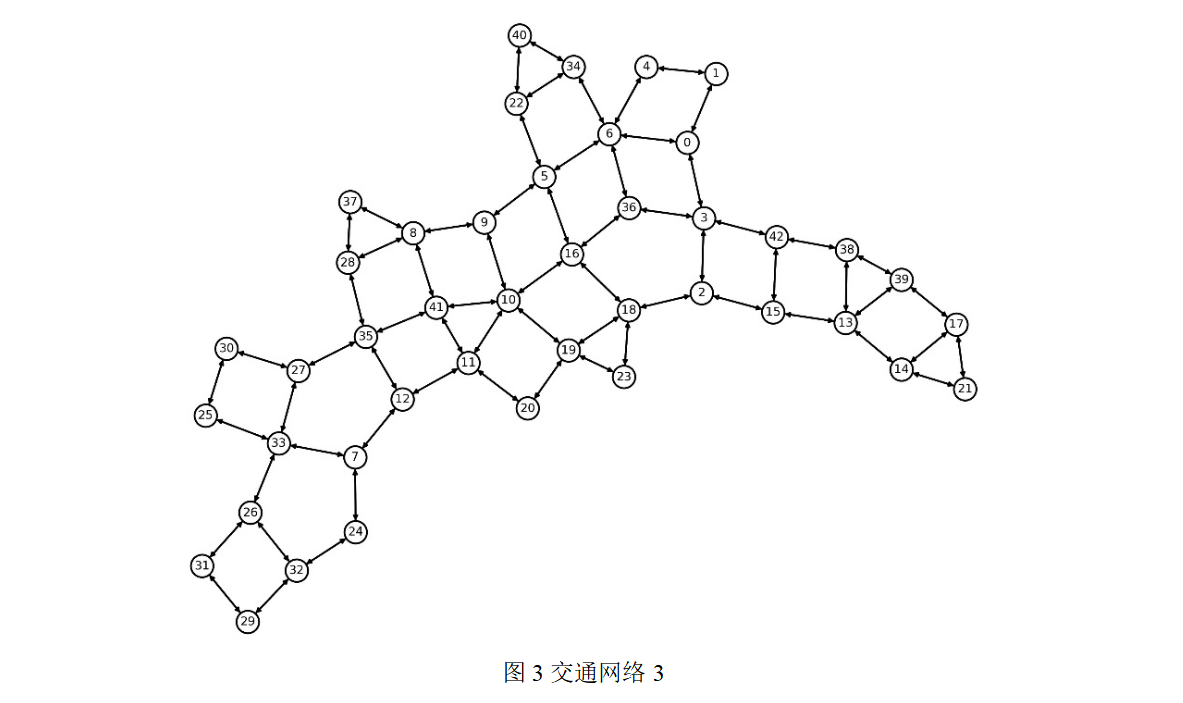
问题3：在交通网络3中，各(起点,终点)对之间的交通需求见附件2，各路段的容量上限见附件3。请建立数学模型，给出各(起点,终点)对之间交通需求分配到对应路径上的交通量，使得网络中任意5条路段出现突发状况时(每个路段出现突发状况概率相同)，网络中所有交通需求的期望可达率最大，且交通需求分配到对应的路径后，各路段上的交通量不能超过路段容量(路段交通量计算方法：路段交通量=经过该路段的路径交通量之和。例如，路径1-0-6与路径1-0-3均经过路段1-0，则路段1-0交通量=路径1-0-6交通量+路径1-0-3交通量)。在表3中填入指定(起点,终点)对规划的路径，以及对应分配的交通量(若规划路径数不足5条无需填满表格)。

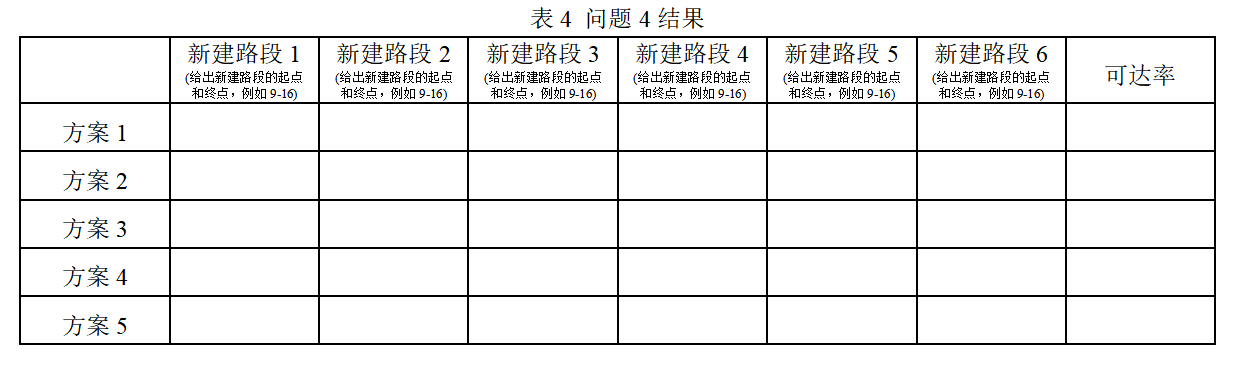
问题4：现计划在交通网络3中新修建6条路段(单向直线路段且长度为单位1，例如节点31至节点32)，新建路段起点和终点必须是交通网络中的任意两个节点，并且假设新建路段的容量足够大。新建路段不能跨越其他路段(例如，不能在节点21与节点39之间修建路段)，只能在网络内部修建(例如，不能在节点4与节点34之间修建路段)。请建立数学模型，给出新修建路段方案，使得在新网络中任意5条路段出现突发事故时(包括新建路段，每个路段出现突发状况概率相同)，网络中所有交通需求的期望可达率尽可能最大，且交通需求分配到对应的路径后，各路段上的交通量不能超过路段容量(新建路段容量足够大，不用考虑这个因素)。在表4中填入期望可达率最大的5种方案及其可达率。

选题分析

A题属于经典的目标优化题型，和往年国赛的椭圆钢板切割非常相似，都构建具体的目标优化函数，使得切割的某个目标最优，从而解得具体参数。

B题涉及到拓扑图论和时间分片动态规划，对于不熟悉这块内容的同学来说，这道题是最难的。

C题老样子，还是数据分析类题目，机器学习类的数据特征分析

本次建模题目难度（由高到低） B > A >C

2 解题思路

问题重述

1. 问题1：要求建立数学模型，针对一个小型交通网络（图2），给出各(起点,终点)对之间的交通需求分配到对应路径上的交通量，以最大化网络中所有交通需求的期望可达率，即使得任意一条路段出现突发状况时，交通需求的满足率最高。需要在表1中填入规划的路径和分配的交通量。

2. 问题2：在更大的交通网络（图3）中，要求建立数学模型，使得在任意5条路段出现突发状况时，网络中所有交通需求的期望可达率最大。同样需要在表2中填入规划的路径和分配的交通量。

3. 问题3：在交通网络3的基础上，考虑各路段的容量上限，建立数学模型以确保在满足可达率最大化的同时，各路段上的交通量不超过其容量上限。需要在表3中填入规划的路径和分配的交通量。

4. 问题4：要求建立数学模型，通过新修建6条路段来提高交通网络的可达率。新建路段的容量足够大，不需要考虑容量限制。需要在表4中填入5种期望可达率最大的新路段方案及其可达率。

简要分析

• 问题1和问题2的核心在于优化交通流的分配，以应对突发状况对交通网络的影响。这涉及到路径选择和流量分配的决策，需要考虑如何在不同的路径之间平衡流量，以确保整体网络的鲁棒性。

• 问题3增加了路段容量的限制，这要求模型在考虑可达率的同时，还要确保不超过路段的承载能力，这增加了问题的复杂性。

• 问题4要求设计新的路段来提升网络的性能，这涉及到网络设计和优化的问题，需要考虑新路段对现有网络结构的影响，以及如何通过这些新路段提高网络的可达率。

解决这些问题需要应用运筹学、网络流理论、概率论和优化技术等数学工具。参赛者需要仔细分析交通网络的结构，考虑不同情况下的交通流量分配，并运用数学建模的方法来找到最优解。

B题4问思路已出，给出了具体的数学描述demo。

详细的思路过程放在文档中 ! ! ！！！！！