动态规划之经典的股票买卖问题详解_从“股票问题”谈动态规划问题的解决思路

开篇

Leetcode上有一组让人头疼的问题——股票买卖问题。这个问题有各种改良版本，于是就延伸出了六种问题。我的不少题友也都和我抱怨过这个问题哪里哪里有坑，哪里哪里不好想到，自己研究了一下发现，这六个题其实就只有一个框架。而整体的框架还是我们上次所说到的找状态，穷举做选择。
昨天有几个朋友看了我的文章之后问我能不能从数学层面解释算法，这里我要说一下，数学对算法固然重要，但是算法最主要的还是一个思想，一个框架，你如果一直热衷于内部的数学原理，其实你很适合学深度学习算法，但这种算法题没有程序员经验的人都可以通过简单的逻辑关系看懂，我们又何必追其繁琐的数学原理?就像你用贪心算法解题的时候，你应该不会再在纸上做一遍数学归纳法来证明这个贪心算法的合理性吧。
所以推荐你看<<算法导论>>的人，要么是真大佬，要就是装大佬，过于强调数学内部原理，用到的数据结构和算法也不是很全面。还是框架最为重要。我们开始吧

问题描述

这是其中的一道题，其实六道题大致描述与这个题目相似，只不过加入了一些额外的条件：
第一题是只进行一次交易，k=1；第二题是不限交易次数，相当于k=正无穷；第三题是只进行两次交易，k=2；剩下的题就是不限任何次数，但是加入了交易冷冻期和手续费的额外条件。

穷举框架
上一篇文章我们的穷举就是对状态进行穷举，这里我们仍然会利用状态进行穷举，后几次我们也会说一些利用递归进行穷举的例子。
我们具体到每一天，看看总共有几种可能的状态，再找出每个状态对应的选择。我们要穷举所有状态，穷举的目的是根据对应的选择更新状态。
给出一个大概的框架：

for 状态1 in 状态1的取值:
	for 状态2 in 状态2的取值:
		for .....
			dp[状态1][状态2][...] = 择优(选择1，选择2,....)
1
2
3

比如说这个问题，我们的状态无非三种：买入、卖出、无操作，我们用buy,sell,rest表示这三种选择。但问题是，并不是每天都可以任意选择这三种选择的，因为sell必须在buy之后，buy必须在sell之后。那么rest应该分两种状态，一种是buy之后的rest(持有股票),一种是sell之后的rest(未持有股票)。而且别忘了，我们还有交易次数k的限制，就是说你buy也只能在k>0的前提下操作。
说了这么多，其实整道题的状态有三个:交易天数，允许交易的最大次数，当前持有的状态(1表示持有，0表示未持有)。列出了三个状态以后，我们就可以根据这三个状态开辟一个三元组，就三种状态组合在一起：

dp[i][k][0 or 1]
0 <= i <= n - 1,1 <= k <= K
n为天数，K为最多交易次数
此问题共有nxKx2种状态，全部穷举就能搞定
 for 0 <=i <= n:
 	for 1 <= k <= K:
 		for s in {0,1}:
 			dp[i][k][s]=max(buy,sell,rest)
1
2
3
4
5
6
7
8

我们用自然语言来解释一下状态内部的含义，比如说dp[3][2][1]的含义是：今天是第二天，我现在手上持有股票，至今最多进行2次交易。
那么理解了这一部分，我们的最终答案就是dp[n-1][K][0]，即最后一天允许进行K次交易，我们最多能获得多少利润(最后一天手上一定未持有股票)
状态转移框架
理解了上面对状态的穷举以及对结果的计算，我们可以用下图来表示状态转移的过程：

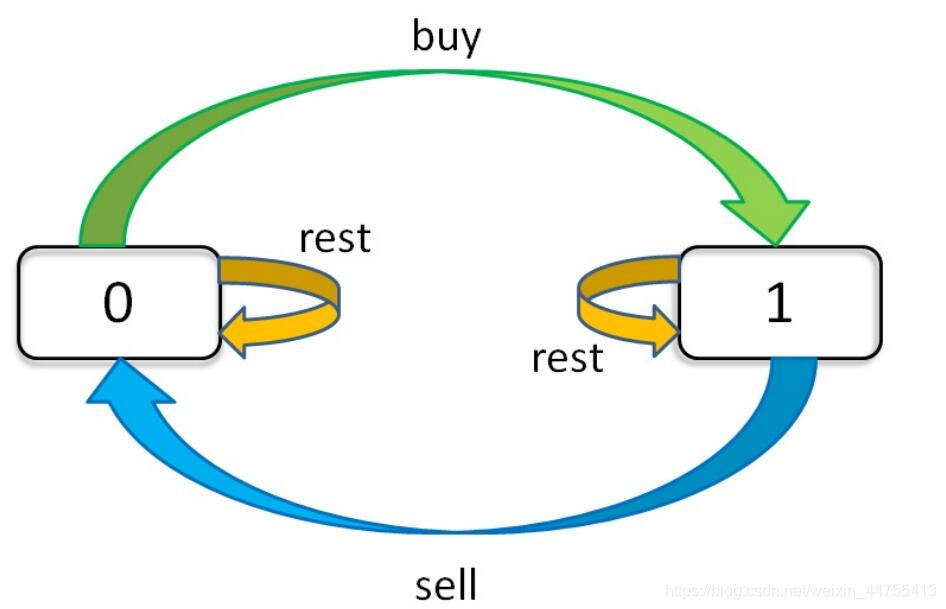
下面就是我们的状态转移方程了，也就是最重要的一部分内容，这里明白了，这六道题都可以直接套用:

dp[i][k][0] = max(dp[i-1][k][0],dp[i-1][k][1] + prices[i]
	      max(**上一状态没有买入这一状态也不买入，上一状态持有股票这一状态将其卖掉**)
这里首先明确一下我们只有在新的一次买入的时候才算进行一次交易，所以这里我们的k没有进行-1操作，因为我们没有买入
dp[i][k][1] = max(dp[i-1][k][1],dp[i-1][k-1][0]-prices[i]
	      max(上一状态持有股票这一状态没有卖出，上一状态未持有股票这一状态买入)
1
2
3
4

买入和卖出肯定是要失去本金和获得利润的，所以我们要+prices[i]或者-prices[i]
现在还差一点点你就可以秒杀所有的问题了，就是动态规划算法的一个主要问题，base case：

dp[-1][k][0] = 0
解释：因为i是从0开始的，所以i=-1意味着还没有开始，这时候的利润当然是0
dp[-1][k][1] = -infinity
解释：还没开始的时候是不可能持有股票的，用负无穷表示这种不可能
dp[i][0][0] = 0
解释：因为k是从1开始的，所以k=0意味着根本不允许进行交易，此时利润是0
dp[i][0][1] = -infinity
解释：不允许交易的情况下，是不可能持有股票的
1
2
3
4
5
6
7

到了这里我们把所有的状态转移方程和base case总结一下:

dp[i][0][1]=dp[-1][0][1] = -infinity
dp[-1][k][0]=dp[i][0][0]=0
状态转移方程:
dp[i][k][0] = max(dp[i-1][k][0],dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1],dp[i-1][k-1][0] - prices[i])
1
2
3
4

实题讲解
OK了，现在万事具备了，我们可以之间秒杀题目了
第一题，k=1
我们可以直接套用我们的状态转移方程和base case

状态转移方程:
dp[i][1][0] = max(dp[i-1][1][0],dp[i-1][1][1] + prices[i])
dp[i][1][1] = max(dp[i-1][1][1],dp[i-1][0][0] - prices[i])
这里面一个比较明显的问题就是k都等于1，且存在一个base case为dp[i-1][0][0]=0
所以我们可以把k省略掉，因为它其实不影响什么因为都是1，而且可以减小空间消耗
dp[i][0] = max(dp[i-1][0],dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1],-prices[i])
1
2
3
4
5
6

直接写出代码：

int n = prices.length;
int[][] dp = new int [n][2];
for(int i = 0;i < n;i++)
{
	dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);
	dp[i][1] = Math.max(dp[i-1][1],-prices[i]);
}
return dp[n-1][0];	
1
2
3
4
5
6
7

显然i==0对dp[i-1]不合法。所以我们要对base case处理一下：

int n = prices.length;
int[][] dp = new int [n][2];
for(int i = 0;i < n;i++)
{
	if(i-1==-1)
	{
		dp[i][0] = 0;
		dp[i][1] = -prices[i];
		continue;
	}
	dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);
	dp[i][1] = Math.max(dp[i-1][1],-prices[i]);
}
return dp[n-1][0]; 
1
2
3
4
5
6
7
8
9
10
11
12
13

第一题就这么轻松的解决了，但其实这并不是最优的方法。
我们可以注意到，我们的新状态只和相邻的一个状态有关，其实不需要整个dp数组，只需要一个变量储存相邻的状态即可，可以将空间复杂度优化到O(1)

int n = prices.length;
int dp_i_0 = 0;
int dp_i_1 = Interger.MIN_VALUE;
for(int i = 0;i < n;i++)
{	
	dp_i_0 = Math.max(dp_i_0,dp_i_1 +prices[i]);
 	dp_i_1 = Math.max(dp_i_1,-prices[i]);
}
return dp_i_0;
1
2
3
4
5
6
7
8

第二题,k=正无穷
如果k为正无穷，那么就认为k和k-1是一样的。可以这样改写框架:

dp[i][k][0] = max(dp[i-1][k][0],dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1],dp[i-1][k-1][0] - prices[i])
但是由于k是正无穷，那么k-1和k就没有了任何区别
所以在这个状态转移方程中，我们的k起不到什么本质的作用
因此我们仍然可以省略掉k
dp[i][0] = max(dp[i-1][0],dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1],dp[i-1][0]-prices[i])
1
2
3
4
5
6
7

直接翻译成代码：

int n = prices.length;
int dp_i_0 = 0;
int dp_i_1 = Interger.MIN_VALUE;
for(int i = 0;i < n;i++)
{ 
	int temp = dp_i_0;
 	dp_i_0 = Math.max(dp_i_0,dp_i_1 +prices[i]);
  	dp_i_1 = Math.max(dp_i_1,temp - prices[i]);
}
return dp_i_0;
1
2
3
4
5
6
7
8
9

当我们只进行一次交易时，买的时候永远都是-prices[i]，所以我们不需要声明一个临时变量temp.但是现在k的次数不限，我们就需要一个temp去记录上一次未持有股票的利润，用这个值减去股票价格就得到了此时持有股票的利润。
第三题.k=正无穷并且带有冷冻期
每次卖出股票之后要等一天才能继续交易，只要把这个特点融合在状态转移方程里即可。

dp[i][0] = max(dp[i-1][0],dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1],dp[i-2][0]-prices[i])
解释：第i天选择buy的时候，要从i-2的状态转移，而不是i-1
1
2

翻译成代码：

int n = prices.length;
int dp_i_0 = 0;
int dp_i_1 = Interger.MIN_VALUE;
int dp_pre_0 = 0;//代表dp[i-2][0]
for(int i = 0;i < n;i++)
{ 
 	int temp = dp_i_0;
  	dp_i_0 = Math.max(dp_i_0,dp_i_1 +prices[i]);
   	dp_i_1 = Math.max(dp_i_1,dp_pre_0 - prices[i]);
   	dp_pre_0 = temp;
}
return dp_i_0;
1
2
3
4
5
6
7
8
9
10
11

这里面temp表示上一状态的dp[i-1][0]，我每次更新temp其实是把上一状态的值赋给它，然后我们更新出当前的两个状态，然后再把temp赋值给temp。此时再次进入循环的时候，dp_pre_0其实是两个状态前的值。
第四题.k=正无穷并且需要手续费
手续费是在购买股票的时候所付的其他费用，所以我们可以改一下状态转移方程：

dp[i][0] = max(dp[i-1][0],dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1],dp[i-1][0]-prices[i]-fee)
解释：相当于买入股票的价格升高了
在第一个式子里减也是一样的，相当于卖出股票的价格减小了
1
2
3

直接翻译成代码:

int n = prices.length;
int dp_i_0 = 0;
int dp_i_1 = Interger.MIN_VALUE;
for(int i = 0;i < n;i++)
{ 
  	int temp = dp_i_0;
   	dp_i_0 = Math.max(dp_i_0,dp_i_1 +prices[i]);
    	dp_i_1 = Math.max(dp_i_1,temp - prices[i] - fee);
 
}
return dp_i_0;
1
2
3
4
5
6
7
8
9
10

第五题.k=2
从这里开始我们有一些说法了，具体是什么说法呢？我们。先看状态转移方程
前面说了，我们要穷举每一个状态，但是前面我们的状态中没有k。那是因为从刚才的状态转移方程可以看出k对结果没有任何影响所以我们省略了它，但是这里我们的k就对状态转移方程有很大的影响了，我们需要也对其进行穷举。
由于k的数目较少，我们可以不在循环中进行直接写出

int n = prices.length;
int dp_i1_0 = 0,dp_i1_1 = Interger.MIN_VALUE;
int dp_i2_0 = 0,dp_i2_1 = Interger.MIN_VALUE;
for(int price:prices)
{ 
	dp_i2_0 = Math.max(dp_i2_0,dp_i2_1 + price);
	dp_i2_1 = Math.max(dp_i2_1,dp_i1_0 - price);
	dp_i1_0 = Math.max(dp_i1_0,dp_i1_1 + price);
	dp_i1_1 = Math.max(dp_i1_1,-price);
	//记住，我们只有在买股票的时候才算一次交易，因此只有买的时候k才会变化
}
return dp_i2_0;
1
2
3
4
5
6
7
8
9
10
11

那如果不用列举而是用循环应该怎么写呢？这就是我们的第六题
第六题.k=任意值
当k为任意值的时候显然不能把k化简，只能利用循环来对k进行穷举。可是我们又不能无脑穷举，为什么呢？思考一下。
我们每两天算一次交易，也就是说，对于n天我们最多可以进行n / 2次交易，这就是我们的交易上限。如果给定的k大于我们的n/2，那么我们就应该将这个问题当作k是无穷大来处理（即上面的第二题），因为k已经超出了上限，我们的天数无法满足，所以此时的k对于我们来说和无穷大毫无区别.（这里可能有点绕大家好好思考一下）
直接对之前的代码进行套用即可:

int maxProfit_k(int max_k,int[] prices)
{	
	int n = prices.length;
	if(max_k > n / 2)
		//调用第二题k是无穷大的函数
		retun maxProfit_k_inf(prices);
	int[][][] dp = new int[n][max_k + 1][2];
	for(int i = 0;i < n;i++)
	{ 
		for(int k = max_k;k >= 1;k--)
		{
			if(i - 1 == -1){//处理一下base case}
			dp[i][k][0] = max(dp[i-1][k][0],dp[i-1][k][1] + prices[i]);
			dp[i][k][1] = ma(dp[i-1][k][1],dp[i-1][k-1][0] - prices[i]);
		}
	}
	retur dp[n-1][max_k][0];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

总结

至此6道题我们都描述完了 ，基本完整的代码也提供给大家了，除了一些少数的需要自己填充的部分。还是那句话，框架最重要。我上面说的所有框架不是让你背的，是要理解的。只要你理解了其内部的逻辑，相信以后类似的问题都可以团灭了。
好啦这次就到这吧。下次也许会谈动态规划法的博弈论问题，或者是用动态规划法的新奇思想解决KMP的问题。