- 1旅行商问题是什么
- 2IS YOU|每周宠读者
- 3卓有成效的管理者|木深读书笔记_高效的经济管理人
- 4亮数据:高效率数据采集,加速大模型训练!_自动化爬虫神器:把网页转成大模型所需数据,助力 ai 应用与大模型训练全面优化!
- 5LLMs-入门二:基于google云端Colab部署Llama 2_llama colab
- 6树莓派上搭建Git服务器_用树莓派做git仓库
- 7【嵌入式Linux项目】基于Linux的全志H616开发板智能家居项目(语音控制、人脸识别、安卓APP和PC端QT客户端远程操控)有视频功能展示_全志h616智能家居
- 8Flink中EventTimeTrigger的理解
- 9女生适合做产品经理吗?_女生做产品经理累吗
- 10大数据技术的发展趋势
java数据结构与算法之顺序表与链表深入分析_public t get(int index)
赞
踩
转载请注明出处(万分感谢!):
http://blog.csdn.net/javazejian/article/details/52953190
出自【zejian的博客】
关联文章:
java数据结构与算法之顺序表与链表设计与实现分析
java数据结构与算法之双链表设计与实现
java数据结构与算法之改良顺序表与双链表类似ArrayList和LinkedList(带Iterator迭代器与fast-fail机制)
java数据结构与算法之栈(Stack)设计与实现
java数据结构与算法之队列(Queue)设计与实现
java数据结构与算法之递归思维(让我们更通俗地理解递归)
java数据结构与算法之树基本概念及二叉树(BinaryTree)的设计与实现
java数据结构与算法之平衡二叉查找树(AVL树)的设计与实现
数据结构与算法这门学科虽然在大学期间就已学习过了,但是到现在确实也忘了不少,因此最近又重新看了本书-《数据结构与算法分析》加上之前看的《java数据结构》也算是对数据结构的进一步深入学习了,于是也就打算写一系列的数据结构的博文以便加深理解,这些博文涵盖了自己对数据结构与算法的理解也包含了这类书籍的基础内容,所以博文中会包含书中的一些概念的引用段落,看到时也不必惊讶,本篇是开篇,主要涵盖顺序表与链表的知识点,关于顺序表与链表将会分两篇博文记录,而本篇将从以下几点出发分析线性表的设计与实现。
1.线性表抽象数据类型概述
首先来说明一下什么是抽象数据类型,我们都知道java在默认情况下,所有的基本数据类型(int,float,boolean等)都支持基本运算,如加减法,这是因为系统已帮我们实现了这些基本数据类型的的基本运算。而对于自定义的数据类型(如类)也需要定义相应的运算,但在实际使用这些自定义的数据类型的运算时需要自己实现相关的运算,也就是说用户自定义的数据类型的运算需要我们自己利用系统提供的基本运算来定义和实现。这些自定义了数据结构(如自定义类)和包含相关运算组合实现的数据类型就称其为抽象数据类型(ADT,Abstract Data Type),因此一个ADT会包含数据声明和运算声明。常用的ADT包含链表、栈、队列、优先队列、二叉树、散列表、图等,所以接下来我们要分析的顺序表和链表也属于ADT范畴。下面引用自java数据结构一书对线性表的定义:
线性表是由n(n>=0)个类型相同的数据元素a0,a1,…,an-1组成的有限的序列,在数学中记作(a0,a1,…,an-1),其中ai的数据类型可以是基本数据类型(int,float等)、字符或类。n代表线性表的元素个数,也称其为长度(Length)。若n=0,则为空表;若n > 0,则ai(0 < i < n-1)有且仅有一个前驱(Predecessor)元素ai-1和一个后继(Successor)元素ai+1,a0没有前驱元素,ai没有后继元素。
以上便是对线性表抽象数据类型概述,下面我们开始分别针对顺序表和链表进行深入分析。
2.线性表的顺序存储设计与实现(顺序表)
2.1 顺序存储结构的设计原理概要
顺序存储结构底层是利用数组来实现的,而数组可以存储具有相同数据类型的元素集合,如int,float或者自定义类型等,当我们创建一个数组时,计算机操作系统会为该数组分配一块连续的内存块,这也就意味着数组中的每个存储单元的地址都是连续的,因此只要知道了数组的起始内存地址就可以通过简单的乘法和加法计算出数组中第n-1个存储单元的内存地址,就如下图所示:

通过上图可以发现为了访问一个数组元素,该元素的内存地址需要计算其距离数组基地址的偏移量,即用一个乘法计算偏移量然后加上基地址,就可以获得数组中某个元素的内存地址。其中c代表的是元素数据类型的存储空间大小,而序号则为数组的下标索引。整个过程需要一次乘法和一次加法运算,因为这两个操作的执行时间是常数时间,所以我们可以认为数组访问操作能再常数时间内完成,即时间复杂度为O(1),这种存取任何一个元素的时间复杂度为O(1)的数据结构称之为随机存取结构。而顺序表的存储原理正如上图所示,因此顺序表的定义如下(引用):
线性表的顺序存储结构称之为顺序表(Sequential List),它使用一维数组依次存放从a0到an-1的数据元素(a0,a1,…,an-1),将ai(0< i <> n-1)存放在数组的第i个元素,使得ai与其前驱ai-1及后继ai+1的存储位置相邻,因此数据元素在内存的物理存储次序反映了线性表数据元素之间的逻辑次序。
2.2 顺序存储结构的实现分析
接着我们来分析一下顺序表的实现,先声明一个顺序表接口类ISeqList<T>,然后实现该接口并实现接口方法的代码,ISeqList接口代码如下:
package com.zejian.structures.LinkedList;
/**
* Created by zejian on 2016/10/30.
* 顺序表顶级接口
*/
public interface ISeqList<T> {
/**
* 判断链表是否为空
* @return
*/
boolean isEmpty();
/**
* 链表长度
* @return
*/
int length();
/**
* 获取元素
* @param index
* @return
*/
T get(int index);
/**
* 设置某个元素的值
* @param index
* @param data
* @return
*/
T set(int index, T data);
/**
* 根据index添加元素
* @param index
* @param data
* @return
*/
boolean add(int index, T data);
/**
* 添加元素
* @param data
* @return
*/
boolean add(T data);
/**
* 根据index移除元素
* @param index
* @return
*/
T remove(int index);
/**
* 根据data移除元素
* @param data
* @return
*/
boolean remove(T data);
/**
* 根据data移除元素
* @param data
* @return
*/
boolean removeAll(T data);
/**
* 清空链表
*/
void clear();
/**
* 是否包含data元素
* @param data
* @return
*/
boolean contains(T data);
/**
* 根据值查询下标
* @param data
* @return
*/
int indexOf(T data);
/**
* 根据data值查询最后一个出现在顺序表中的下标
* @param data
* @return
*/
int lastIndexOf(T data);
/**
* 输出格式
* @return
*/
String toString();
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
代码中声明了一个Object数组,初始化数组大小默认为64,存储的元素类型为泛型T,length则为顺序表的长度,部分方法实现比较简单,这里不过多分析,我们主要分析get(int index)、set(int index, T data)、add(int index, T data)、remove(int index)、removeAll(T data)、indexof(T data)等方法的实现。
get(int index) 实现分析
从顺序表中获取值是一种相当简单的操作并且效率很高,这是由于顺序表内部采用了数组作为存储数据的容器。因此只要根据传递的索引值,然后直接获取数组中相对应下标的值即可,代码实现如下:public T get(int index){ if (index>=0 && index<this.length) return (T) this.table[index]; return null; }- 1
- 2
- 3
- 4
- 5
set(int index, T data) 实现分析
在顺序表中替换值也是非常高效和简单的,只要根据传递的索引值index找到需要替换的元素,然后把对应元素值替换成传递的data值即可,代码如下:public T set(int index, T data){ if (index>=0 && index<this.length&& data!=null) { T old = (T)this.table[index]; this.table[index] = data; return old; } return null; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
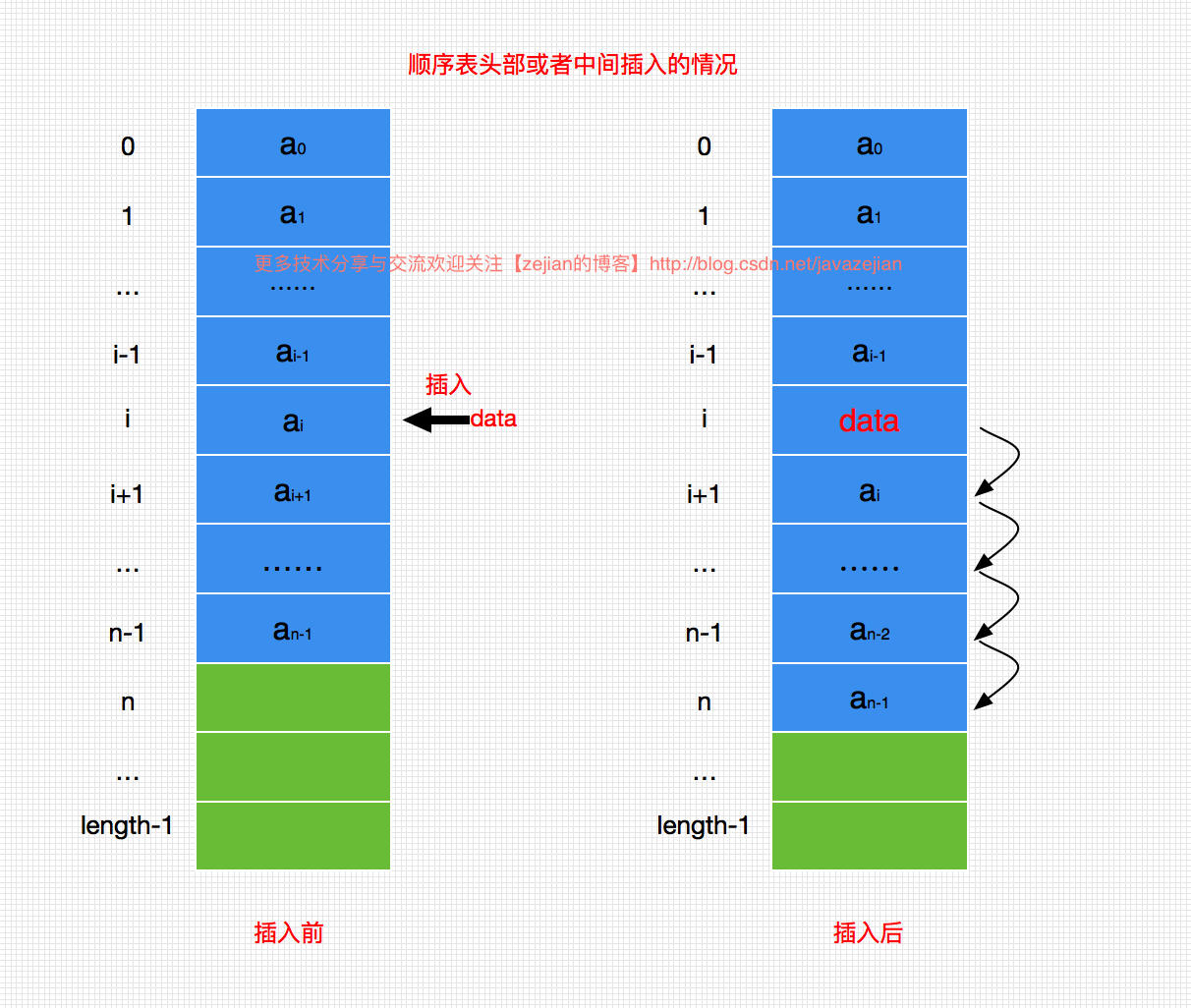
add(int index, T data)实现分析
在顺序表中执行插入操作时,如果其内部数组的容量尚未达到最大值时,可以归结为两种情况,一种是在头部插入或者中间插入,这种情况下需要移动数组中的数据元素,效率较低,另一种是在尾部插入,无需移动数组中的元素,效率高。但是当顺序表内部数组的容量已达到最大值无法插入时,则需要申请另一个更大容量的数组并复制全部数组元素到新的数组,这样的时间和空间开销是比较大的,也就导致了效率更为糟糕了。因此在插入频繁的场景下,顺序表的插入操作并不是理想的选择。下面是顺序表在数组容量充足下头部或中间插入操作示意图(尾部插入比较简单就不演示了):
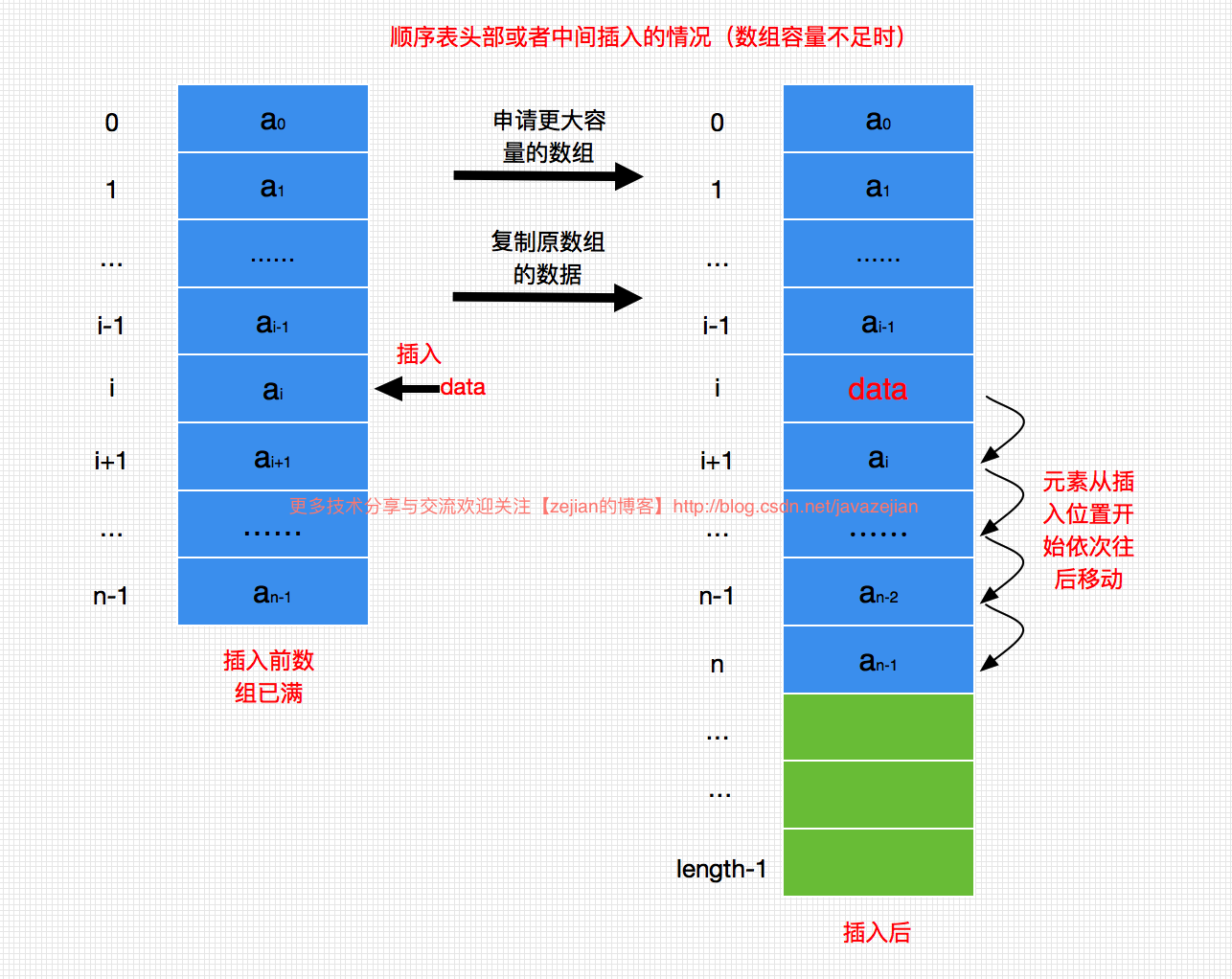
顺序表在数组容量不充足的情况下头部或中间插入操作示意图:
理解了以上几种顺序表的插入操作后,我们通过代码来实现这个插入操作如下,注释很清晰就过多分析了:/** * 根据index插入元素 * @param index 插入位置的下标,0作为起始值 * @param data 插入的数据 * @return */ public boolean add(int index, T data){ if (data==null) return false; //插入下标的容错判断,插入在最前面 if (index<0) index=0; //插入下标的容错判断,插入在最后面 if (index>this.length) index = this.length; //判断内部数组是否已满 if (this.length==table.length) { //把原数组赋值给临时数组 Object[] temp = this.table; //对原来的数组进行成倍拓容,并把原数组的元素复制到新数组 this.table = new Object[temp.length*2]; //先把原数组下标从0到index-1(即插入位置的前一个位置)复制到新数组 for (int i=0; i<index; i++) { this.table[i] = temp[i]; } } //从原数组的最后一个元素开始直到index位置,都往后一个位置 // 最终腾出来的位置就是新插入元素的位置了 for (int j=this.length-1; j>=index; j--) { this.table[j + 1] = this.table[j]; } //插入新值 this.table[index] = data; //长度加一 this.length++; //插入成功 return true; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
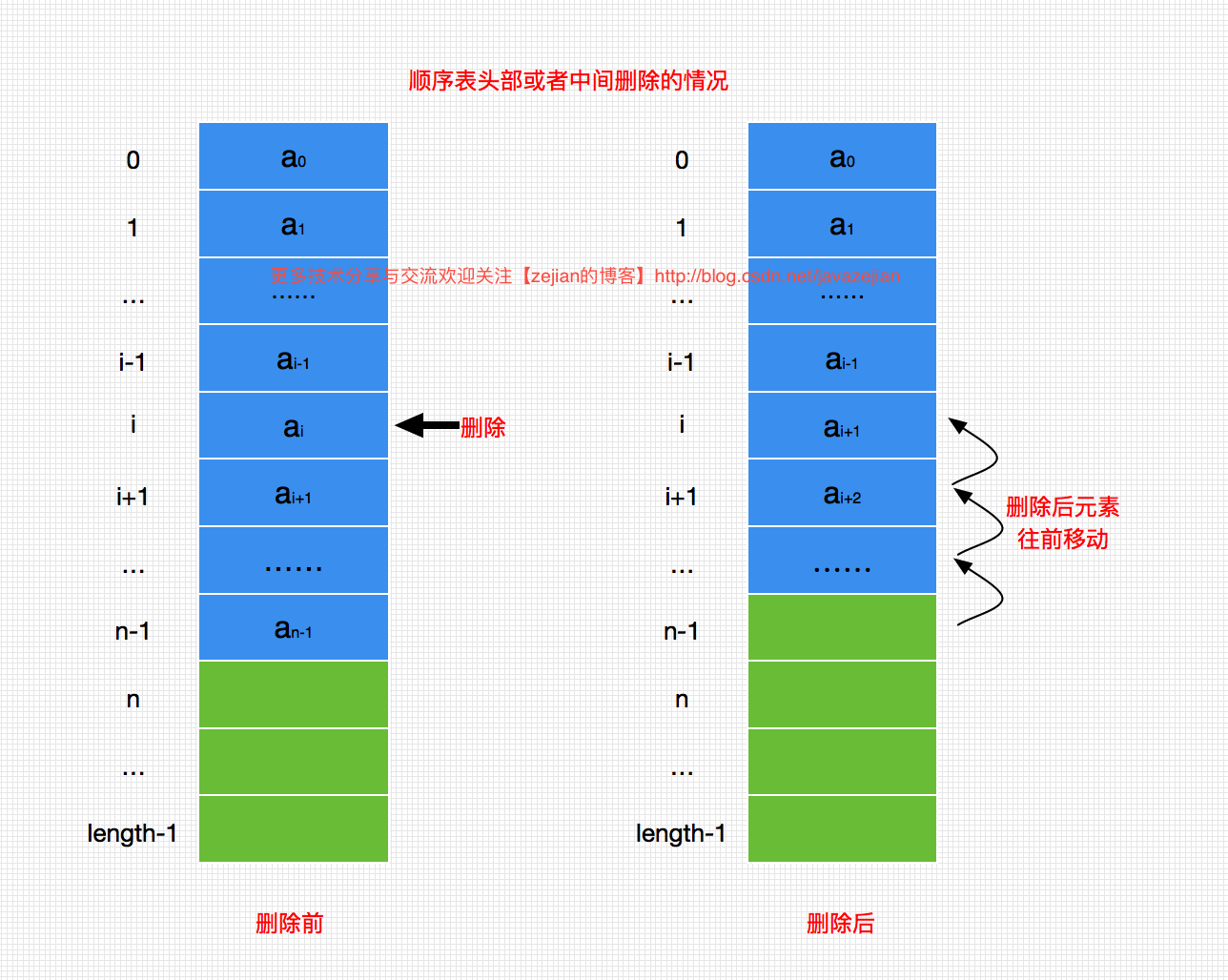
remove(int index) 实现分析
顺序表的删除操作和前的插入操作情况是类似的,如果是在中间或者头部删除顺序表中的元素,那么在删除位置之后的元素都必须依次往前移动,效率较低,如果是在顺序表的尾部直接删除的话,则无需移动元素,此情况下删除效率高。如下图所示在顺序表中删除元素ai时,ai之后的元素都依次往前移动:
删除操作的代码实现如下:/** * 根据index删除元素 * @param index 需要删除元素的下标 * @return */ public T remove(int index) { if (this.length!=0 && index>=0 && index<this.length) { //记录删除元素的值并返回 T old = (T)this.table[index]; //从被删除的元素位置开,其后的元素都依次往前移动 for (int j=index; j<this.length-1; j++) { this.table[j] = this.table[j + 1]; } //设置数组元素对象为空 this.table[this.length-1]=null; //顺序表长度减1 this.length--; return old; } return null; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
removeAll(T data) 实现分析
在顺序表中根据数据data找到需要删除的数据元素和前面分析的根据index删除顺序表中的数据元素是一样的道理,因此我们只要通过比较找到与data相等的数据元素并获取其下标,然后调用前面实现的remove(int index)方法来移除即可。代码实现如下:@Override public boolean removeAll(T data) { boolean done=false; if (this.length!=0 && data!=null) { int i=0; while (i<this.length) //找出数据相同的选项 if (data.equals(this.table[i])) { this.remove(i);//根据下标删除 done = true; } else i++;//继续查找 } return done; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
indexOf(T data) 实现分析
要根据data在顺序表中查找第一个出现的数据元素的下标,只需要通过对比数据项是否相等,相等则返回下标,不相等则返回-1,indexOf和lastIndexOf方法实现如下:/** * 根据数据查询下标 * @param data * @return */ @Override public int indexOf(T data) { if (data!=null) for (int i=0; i<this.length; i++) { //相当则返回下标 if (this.table[i].equals(data)) return i; } return -1; } /** * 根据data查询最后一个出现在顺序表中的下标 * @param data * @return */ @Override public int lastIndexOf(T data) { if (data!=null) for (int i=this.length-1; i>=0; i--) if (data.equals(this.table[i])) return i; return -1; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
以上便是顺序表的主要的操作方法,当然顺序表中还可以实现其他操作,如在初始化构造函数时传入数组来整体初始化顺序表,比较两个信息表是否相等、是否包含某个数据等。这里贴一下传入数据构建顺序表构造方法实现,其他实现代码我们这里就不贴了,稍后实现源码都会上传gitHub提供给大家:
/**
* 传入一个数组初始化顺序表
* @param array
*/
public SeqList(T[] array){
if (array==null){
throw new NullPointerException("array can\'t be empty!");
}
//创建对应容量的数组
this.table = new Object[array.length];
//复制元素
for (int i=0;i<array.length;i++){
this.table[i]=array[i];
}
this.length=array.length;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
2.3 顺序存储结构的效率分析
通过上述的分析,我们对顺序表的实现已有了比较清晰的认识,接下来看一下顺序表的执行效率问题,主要针对获取、插入、修改、删除等主要操作。前面分析过,由于顺序表内部采用了数组作为存储容器,而数组又是随机存取结构的容器,也就是说在创建数组时操作系统给数组分配的是一块连续的内存空间,数组中每个存储单元的地址都是连续的,所以在知道数组基地址后可以通过一个简单的乘法和加法运算即可计算出其他存储单元的内存地址(实际上计算机内部也就是这么做的),这两个运算的执行时间是常数时间,因此可以认为数组的访问操作能在常数时间内完成,即顺序表的访问操作(获取和修改元素值)的时间复杂为O(1)。
对于在顺序表中插入或者删除元素,从效率上则显得不太理想了,由于插入或者删除操作是基于位置的,需要移动数组中的其他元素,所以顺序表的插入或删除操作,算法所花费的时间主要是用于移动元素,如在顺序表头部插入或删除时,效率就显得相当糟糕了。若在最前插入或删除,则需要移动n(这里假设长度为n)个元素;若在最后插入或删除,则需要移动的元素为0。这里我们假设插入或删除值为第i(0<i<=n)个元素,其概率为pi
p1∗(n−1)+p2∗(n−2)+...+pi∗(n−i)+...+pn−1∗1+pn∗0=n∑i=1(pi∗(n−i))p1∗(n−1)+p2∗(n−2)+...+pi∗(n−i)+...+pn−1∗1+pn∗0=∑i=1n(pi∗(n−i))
如果在各个位置插入元素的概率相同即 pi=1n+1 (n+1个插入位置任意选择一个的概率)则有:
n∑i=1(pi∗(n−i))=1n+1n∑i=1(n−i)=1n+1∗n(n+1)2=n2=O(n)
也就是说,在等概率的情况下,插入或者删除一个顺序表的元素平均需要移动顺序表元素总量的一半,其时间复杂度是O(n)。当然如果在插入时,内部数组容量不足时,也会造成其他开销,如复制元素的时间开销和新建数组的空间开销。
因此总得来说顺序表有以下优缺点:
优点
使用数组作为内部容器简单且易用
在访问元素方面效率高
数组具有内存空间局部性的特点,由于本身定义为连续的内存块,所以任何元素与其相邻的元素在物理地址上也是相邻的。
缺点
内部数组大小是静态的,在使用前必须指定大小,如果遇到容量不足时,需动态拓展内部数组的大小,会造成额外的时间和空间开销
在内部创建数组时提供的是一块连续的空间块,当规模较大时可能会无法分配数组所需要的内存空间
- 顺序表的插入和删除是基于位置的操作,如果需要在数组中的指定位置插入或者删除元素,可能需要移动内部数组中的其他元素,这样会造成较大的时间开销,时间复杂度为O(n)
3.线性表的链式存储设计与实现(链表)
3.1 链表的链式存储结构设计原理概要
通过前面对线性顺序表的分析,我们知道当创建顺序表时必须分配一块连续的内存存储空间,而当顺序表内部数组的容量不足时,则必须创建一个新的数组,然后把原数组的的元素复制到新的数组中,这将浪费大量的时间。而在插入或删除元素时,可能需要移动数组中的元素,这也将消耗一定的时间。鉴于这种种原因,于是链表就出场了,链表在初始化时仅需要分配一个元素的存储空间,并且插入和删除新的元素也相当便捷,同时链表在内存分配上可以是不连续的内存,也不需要做任何内存复制和重新分配的操作,由此看来顺序表的缺点在链表中都变成了优势,实际上也是如此,当然链表也有缺点,主要是在访问单个元素的时间开销上,这个问题留着后面分析,我们先通过一张图来初步认识一下链表的存储结构,如下:
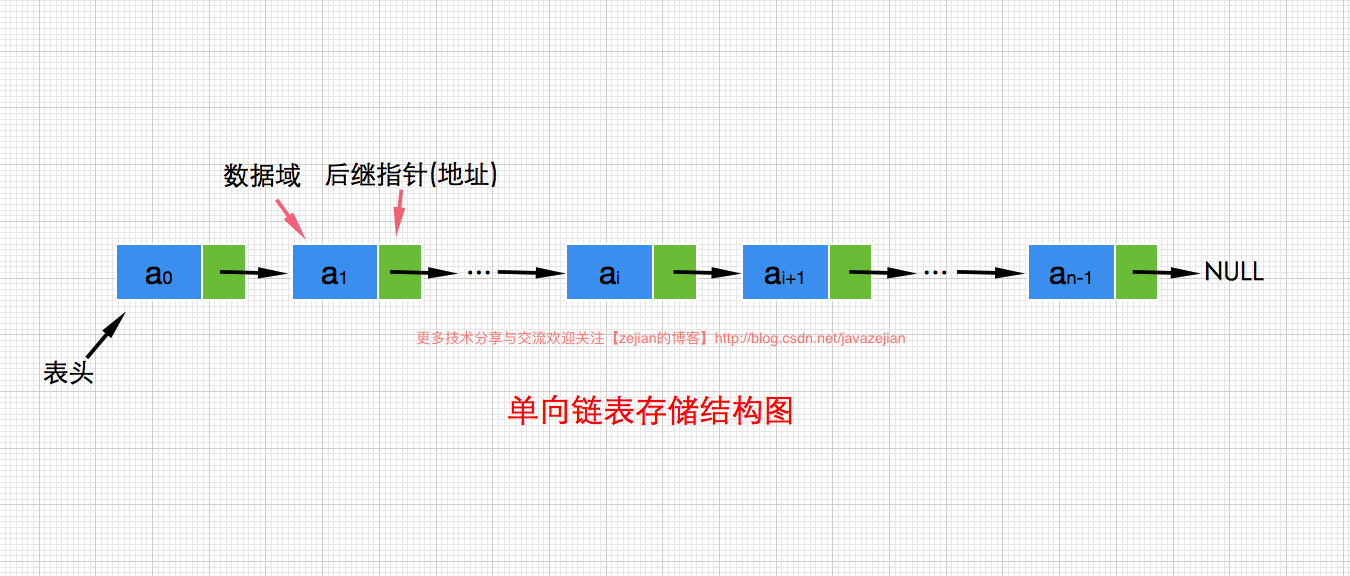
从图可以看出线性链表的存储结构是用若干个地址分散的存储单元存放数据元素的,逻辑上相邻的数据元素在物理位置上不一定相邻,因此每个存储单元中都会有一个地址指向域,这个地址指向域指明其后继元素的位置。在链表中存储数据的单元称为结点(Node),从图中可以看出一个结点至少包含了数据域和地址域,其中数据域用于存储数据,而地址域用于存储前驱或后继元素的地址。前面我们说过链表的插入和删除都相当便捷,这是由于链表中的结点的存储空间是在插入或者删除过程中动态申请和释放的,不需要预先给单链表分配存储空间的,从而避免了顺序表因存储空间不足需要扩充空间和复制元素的过程,提高了运行效率和存储空间的利用率。
3.2 单链表的储结构实现分析
到此我们已初步了解了链表的概念和存储结构,接下来,开始分析链表的实现,这里先从单链表入手。同样地,先来定义一个顶级的链表接口:ILinkedList和存储数据的结点类Node,该类是代表一个最基本的存储单元,Node代码如下:
/**
* Created by zejian on 2016/10/21.
* 单向链表节点
*/
public class Node<T> {
public T data;//数据域
public Node<T> next;//地址域
public Node(T data){
this.data=data;
}
public Node(T data,Node<T> next){
this.data=data;
this.next=next;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
接着顶级的链表接口ILinkedList,该接口声明了我们所有需要实现的方法。
/**
* Created by zejian on 2016/10/21.
* 链表顶级接口
*/
public interface ILinkedList<T> {
/**
* 判断链表是否为空
* @return
*/
boolean isEmpty();
/**
* 链表长度
* @return
*/
int length();
/**
* 获取元素
* @param index
* @return
*/
T get(int index);
/**
* 设置某个结点的的值
* @param index
* @param data
* @return
*/
T set(int index, T data);
/**
* 根据index添加结点
* @param index
* @param data
* @return
*/
boolean add(int index, T data);
/**
* 添加结点
* @param data
* @return
*/
boolean add(T data);
/**
* 根据index移除结点
* @param index
* @return
*/
T remove(int index);
/**
* 根据data移除结点
* @param data
* @return
*/
boolean removeAll(T data);
/**
* 清空链表
*/
void clear();
/**
* 是否包含data结点
* @param data
* @return
*/
boolean contains(T data);
/**
* 输出格式
* @return
*/
String toString();
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
创建一个单链表SingleILinkedList并实现ILinkedList接口,覆盖其所有方法,声明一个单链表的头结点head,代表链表的开始位置,如下:
public class SingleILinkedList<T> implements ILinkedList<T> {
protected Node<T> headNode; //带数据头结点
public SingleILinkedList(Node<T> head) {
this.headNode = head;
}
//其他代码先省略
.....
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
boolean isEmpty()实现分析
需要判断链表是否为空的依据是头结点head是否为null,当head=null时链表即为空链表,因此我们只需判断头结点是否为空即可,isEmpty方法实现如下:/** * 判断链表是否为空 * @return */ @Override public boolean isEmpty() { return this.head==null; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
int length()实现分析
由于单链表的结点数就是其长度,因此我们只要遍历整个链表并获取结点的数量即可获取到链表的长度。遍历链表需要从头结点HeadNode开始,为了不改变头结点的存储单元,声明变量p指向当前头结点和局部变量length,然后p从头结点开始访问,沿着next地址链到达后继结点,逐个访问,直到最后一个结点,每经过一个结点length就加一,最后length的大小就是链表的大小。实现代码如下:@Override public int length() { int length=0;//标记长度的变量 Node<T> p=head;//变量p指向头结点 while (p!=null){ length++; p=p.next;//后继结点赋值给p,继续访问 } return length; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
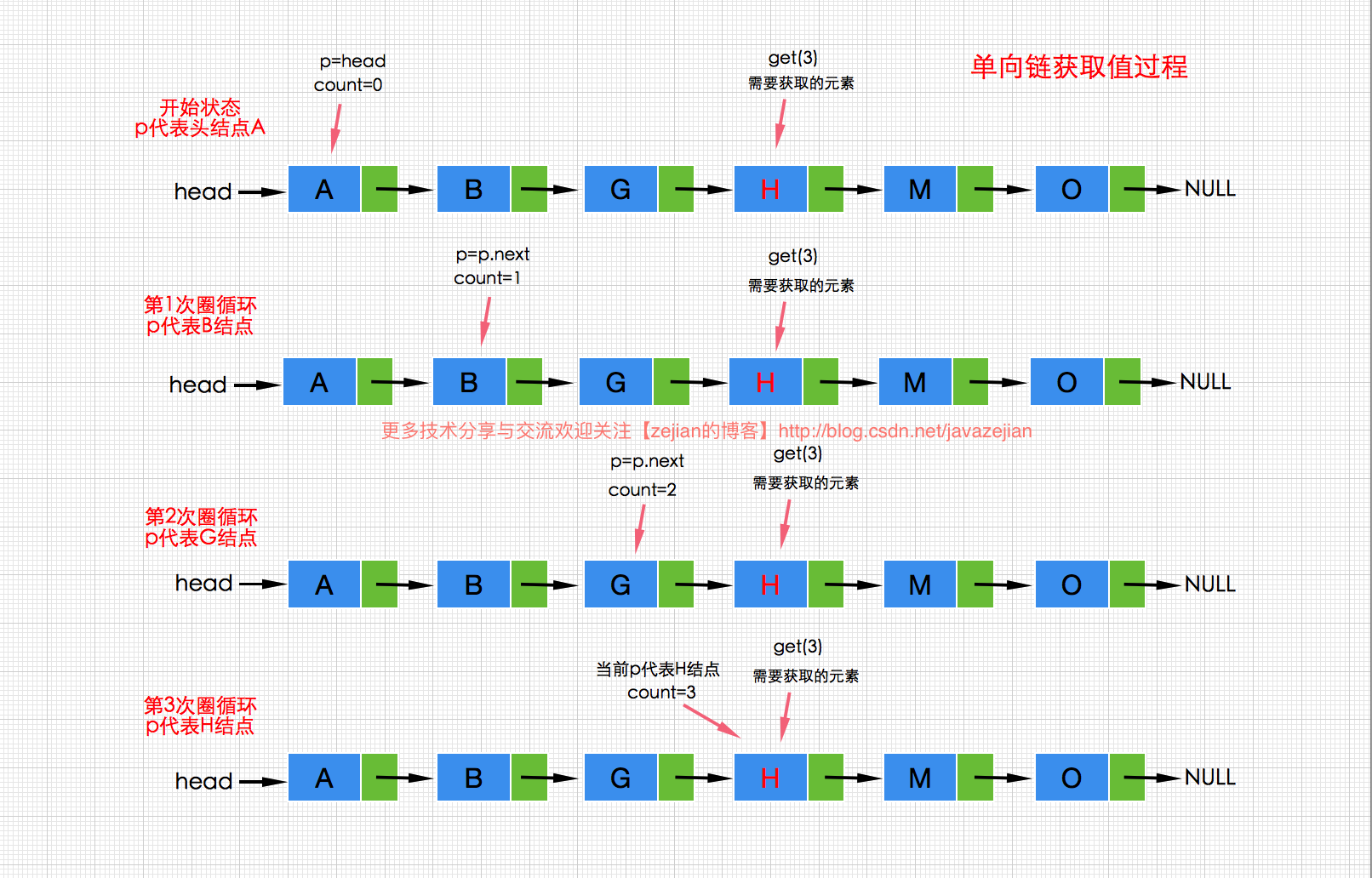
T get(int index)实现分析
在单链表中获取某个元素的值是一种比较费时间的操作,需要从头结点开始遍历直至传入值index指向的位置,其中需要注意的是index是从0开始计算,也就是说传递的index=3时,查找的是链表中第4个位置的值。其查询获取值的过程如下图所示:
代码实现如下:/** * 根据index索引获取值 * @param index 下标值起始值为0 * @return */ @Override public T get(int index) { if(this.head!=null&&index>=0){ int count=0; Node<T> p=this.head; //找到对应索引的结点 while (p!=null&&count<index){ p=p.next; count++; } if(p!=null){ return p.data; } } return null; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
通过上图和代码,我们就可以很容易理解链表中取值操作的整个过程了。
T set(int index, T data)实现分析
根据传递的index查找某个值并替换其值为data,其实现过程的原理跟get(int index)是基本一样的,先找到对应值所在的位置然后删除即可,不清晰可以看看前面的get方法的图解,这里直接给出代码实现:/** * 根据索引替换对应结点的data * @param index 下标从0开始 * @param data * @return 返回旧值 */ @Override public T set(int index, T data) { if(this.head!=null&&index>=0&&data!=null){ Node<T> pre=this.head; int count=0; //查找需要替换的结点 while (pre!=null&&count<index){ pre=pre.next; count++; } //不为空直接替换 if (pre!=null){ T oldData=pre.data; pre.data=data;//设置新值 return oldData; } } return null; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
add(int index, T data)实现分析
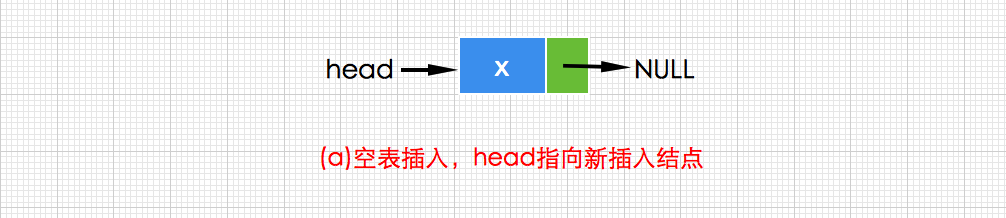
单链表的插入操作分四种情况:
a.空表插入一个新结点,插语句如下:head=new Node<T>(x,null);- 1
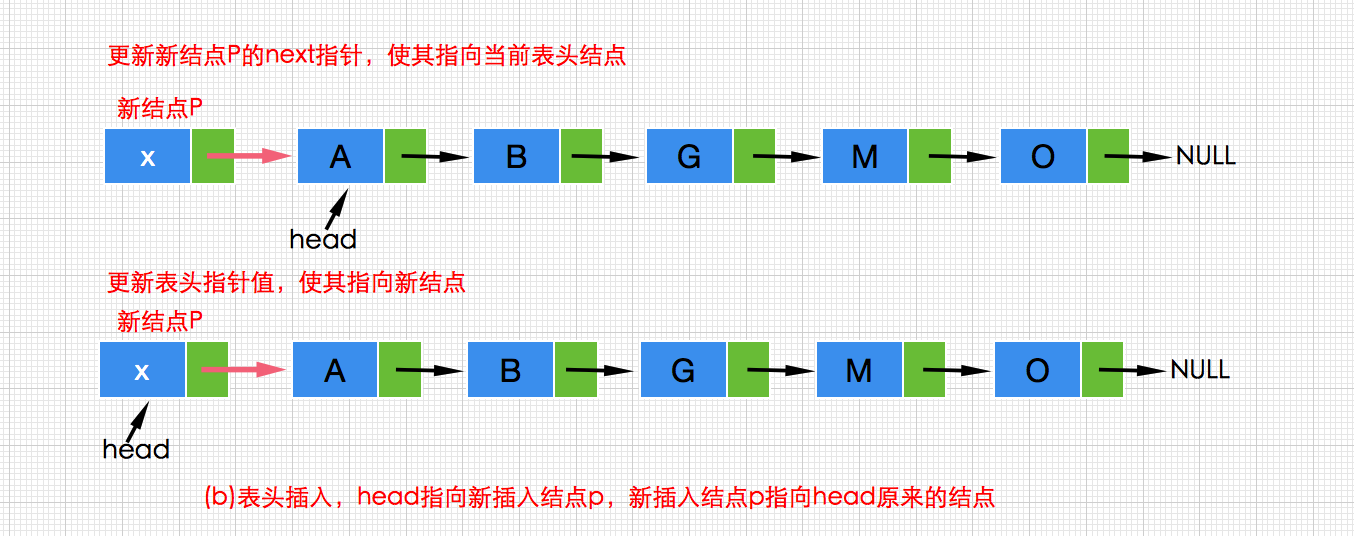
b.在链表的表头插入一个新结点(即链表的开始处),此时表头head!=null,因此head后继指针next应该指向新插入结点p,而p的后继指针应该指向head原来的结点,代码如下:
//创建新结点 Node<T> p =new Node<T>(x,null); //p的后继指针指向head原来的结点 p.next=head; //更新head head=p;- 1
- 2
- 3
- 4
- 5
- 6
以上代码可以合并为如下代码:
//创建新结点,其后继为head原来的结点,head的新指向为新结点 head=new Node<T>(x,head);- 1
- 2
执行过程如下图:
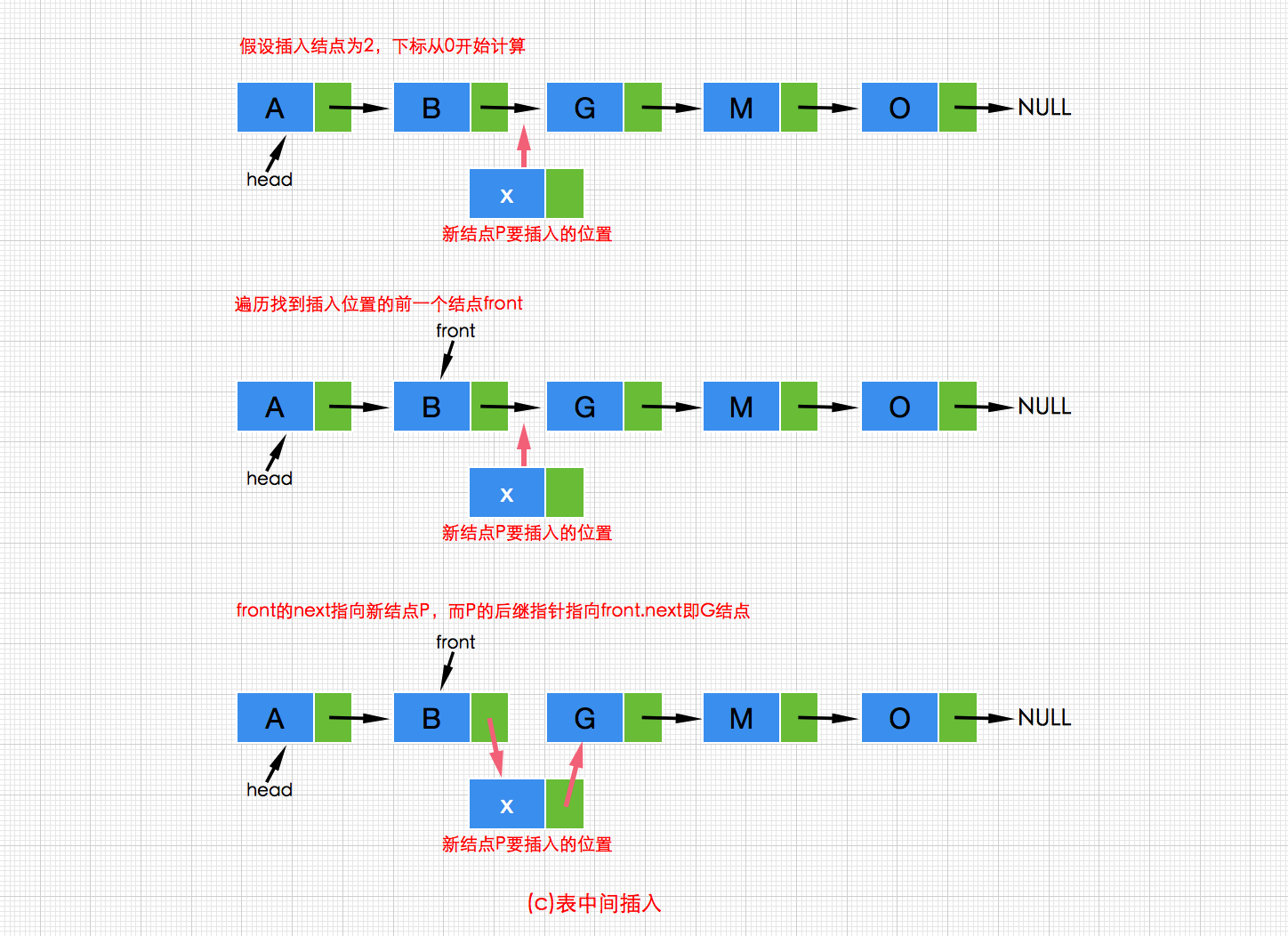
c.在链表的中间插入一个新结点p,需要先找到给定插入位置的前一个结点,假设该结点为front,然后改变front的后继指向为新结点p,同时更新新结点p的后继指向为front原来的后继结点,即front.next,其执行过程如下图所示:
代码实现如下://新结点p Node<T> p =new Node<T>(x,null); //更新p的后继指向 p.next=front.next; //更新front的后继指向 front.next=p;- 1
- 2
- 3
- 4
- 5
- 6
以上三句代码合并为一句简洁代码:
front.next=new Node<T>(x,front.next);- 1
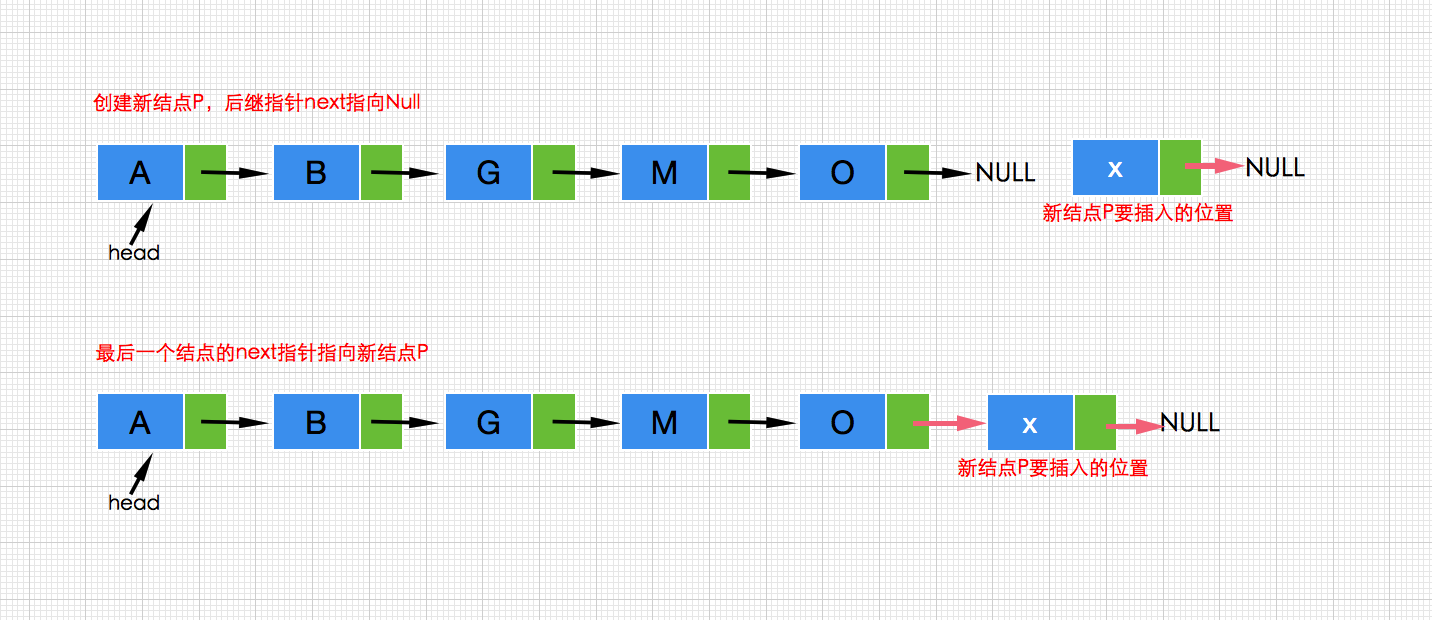
d.在链表的表尾插入一个新结点(链表的结尾)在尾部插入时,同样需要查找到插入结点P的前一个位置的结点front(假设为front),该结点front为尾部结点,更改尾部结点的next指针指向新结点P,新结点P的后继指针设置为null,执行过程如下:
其代码语句如下://front的next指针指向新结点,新结点的next指针设置为null front.next=new Node<T>(x,null);- 1
- 2
到此我们也就可以发现单向链表中的中间插入和尾部插入其实可以合并为一种情况。最后这里给出该方法整体代码实现,从代码实现上来看中间插入和尾部插入确实也视为同种情况处理了。
/** * 根据下标添加结点 * 1.头部插入 * 2.中间插入 * 3.末尾插入 * @param index 下标值从0开始 * @param data * @return */ @Override public boolean add(int index, T data) { if (data==null){ return false; } //在头部插入 if (this.head==null||index<=1){ this.head = new Node<T>(data, this.head); }else { //在尾部或中间插入 int count=0; Node<T> front=this.head; //找到要插入结点位置的前一个结点 while (front.next!=null&&count<index-1){ front=front.next; count++; } //尾部添加和中间插入属于同种情况,毕竟当front为尾部结点时front.next=null front.next=new Node<T>(data,front.next); } return true; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
T remove(int index) 删除结点实现分析
在单向链表中,根据传递index位置删除结点的操作分3种情况,并且删除后返回被删除结点的数据:
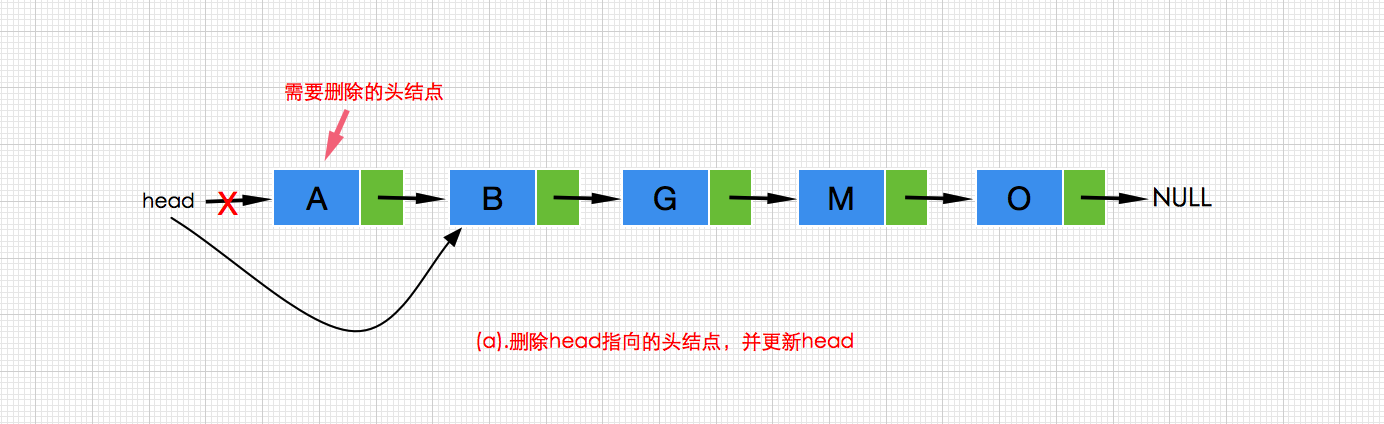
a.删除链表头部(第一个)结点,此时需要删除头部head指向的结点,并更新head的结点指向,执行图示如下:
代码实现如下://头部删除,更新head指向 head=head.next;- 1
- 2
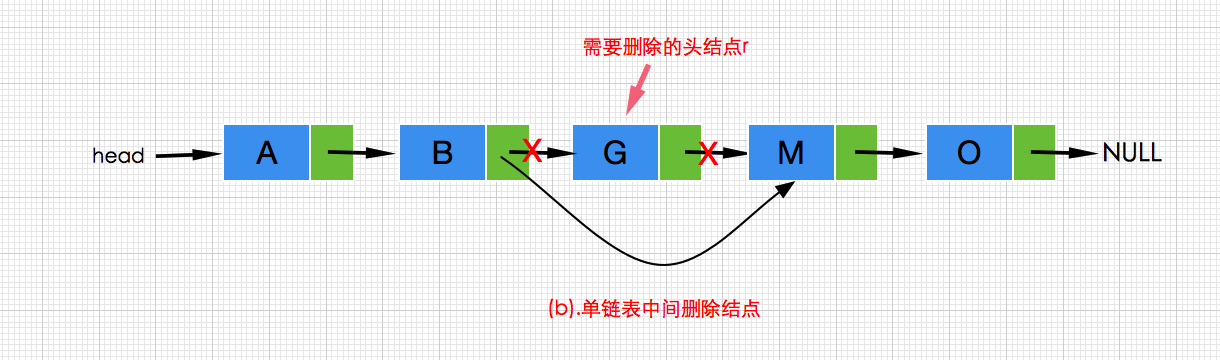
b.删除链表的中间结点,与添加是同样的道理,需要先找到要删除结点r(假设要删除的结点为r)位置的前一个结点front(假设为front),然后把front.next指向r.next即要删除结点的下一个结点,执行过程如下:
代码语句如下:Node<T> r =front.next; //更新结点指针指向 front.next=r.next; r=null;- 1
- 2
- 3
- 4
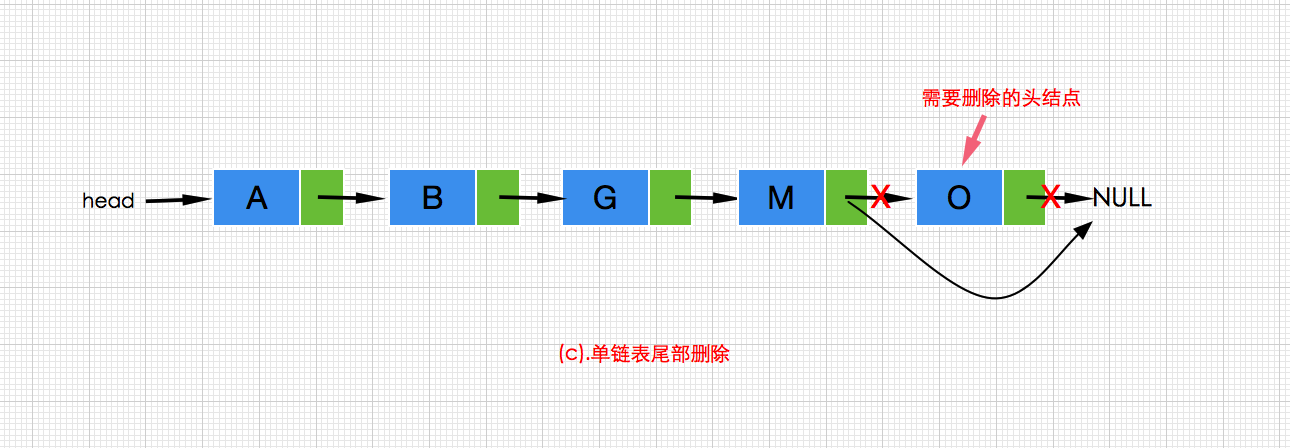
c.删除链表的最后一个结点,通过遍历操作找到最后一个结点r的前一个结点front,并把front.next设置为null,即可。执行过程如下:
代码如下:front.next=null; r=null;- 1
- 2
我们把中间删除和尾部删除合并为如下代码:
Node<T> r =front.next; //如果不是尾部结点,更新结点front指针指向 if(r=!null){ front.next=r.next; r=null; }- 1
- 2
- 3
- 4
- 5
- 6
该方法整体代码实现如下:
/** * 根据索引删除结点 * @param index * @return */ @Override public T remove(int index) { T old=null; if (this.head!=null&&index>=0){ //直接删除的是头结点 if(index==0){ old=this.head.data; this.head=this.head.next; }else { Node<T> front = this.head; int count = 0; //查找需要删除结点的前一个结点 while (front.next != null && count < index - 1) { front = front.next; count++; } //获取到要删除的结点 Node<T> r = front.next; if ( r!= null) { //获取旧值 old =r.data; //更改指针指向 front.next=r.next; //释放 r=null; } } } return old; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
当然还有如下更简洁的代码写法:
@Override public T remove(int index) { T old=null; if (this.head!=null&&index>=0){ //直接删除的是头结点 if(index==0){ old=this.head.data; this.head=this.head.next; }else { Node<T> front = this.head; int count = 0; //查找需要删除结点的前一个结点 while (front.next != null && count < index - 1) { front = front.next; count++; } if ( front.next!= null) { //获取旧值 old =front.next.data; //更改指针指向 front.next=front.next.next; } } } return old; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
void clear() 实现分析
清空链表是一件非常简单的事,只需让head=null即可;代码如下:/** * 清空链表 */ @Override public void clear() { this.head=null; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
ok~,到此单链表主要的添加、删除、获取值、设置替换值、获取长度等方法已分析完毕,其他未分析的方法都比较简单这里就不一一分析了,单链表的整体代码最后会分享到github给大家。
3.3 带头结点的单链表以及循环单链表的实现
带头结点的单链表
前面分析的单链表是不带特殊头结点的,所谓的特殊头结点就是一个没有值的结点即:
//没有带值的头结点
Node<T> head= new Node<T>(null,null);- 1
- 2
此时空链表的情况如下:

那么多了头结点的单向链表有什么好处呢?通过对没有带头结点的单链表的分析,我们可以知道,在链表插入和删除时都需要区分操作位,比如插入操作就分头部插入和中间或尾部插入两种情况(中间或尾部插入视为一种情况对待即可),如果现在有不带数据的头结点,那么对于单链表的插入和删除不再区分操作的位置,也就是说头部、中间、尾部插入都可以视为一种情况处理了,这是因为此时头部插入和头部删除无需改变head的指向了,头部插入如下所示:
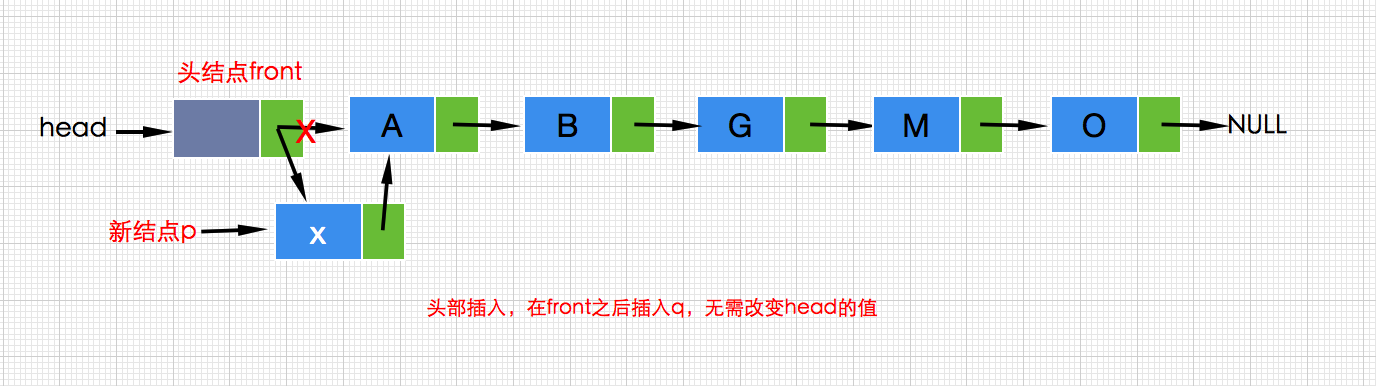
接着再看看在头部删除的情况:
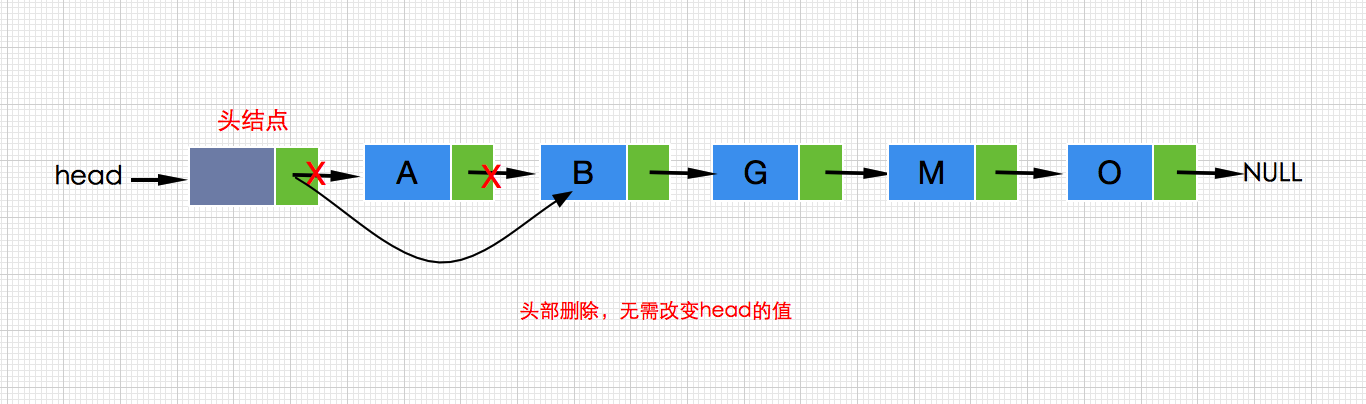
带头结点遍历从head.next开始:
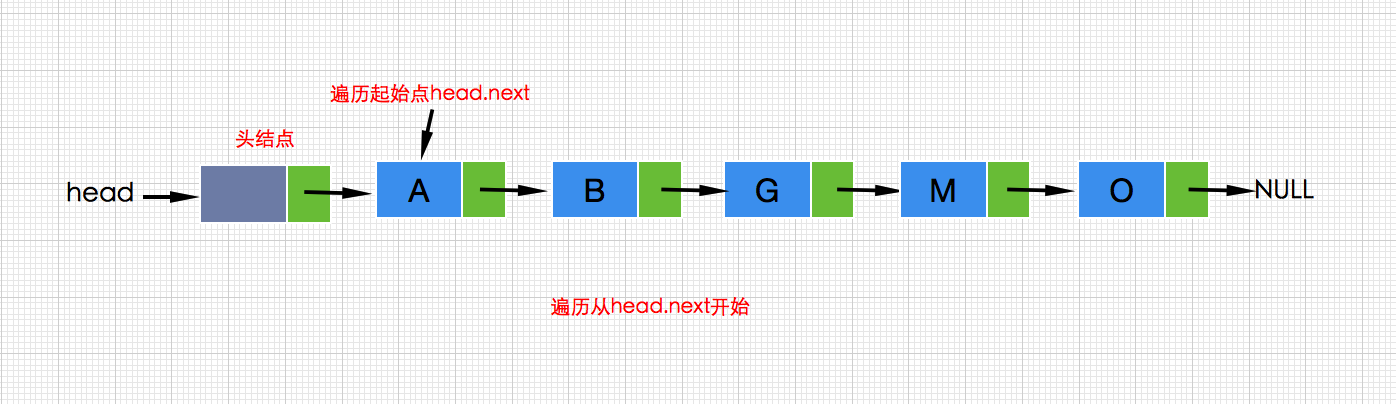
因此无论是插入还是删除,在有了不带数据的头结点后,在插入或者删除时都无需区分操作位了,好~,到此我们来小结一下带头结点的单链表特点:
- a.空单链表只有一个结点,head.next=null。
- b.遍历的起点为p=head.next。
- c.头部插入和头部删除无需改变head的指向。
同时为了使链表在尾部插入时达到更加高效,我们可在链表内增加一个尾部指向的结点rear,如果我们是在尾部添加结点,那么此时只要通过尾部结点rear进行直接操作即可,无需从表头遍历到表尾,带尾部结点的单链表如下所示:
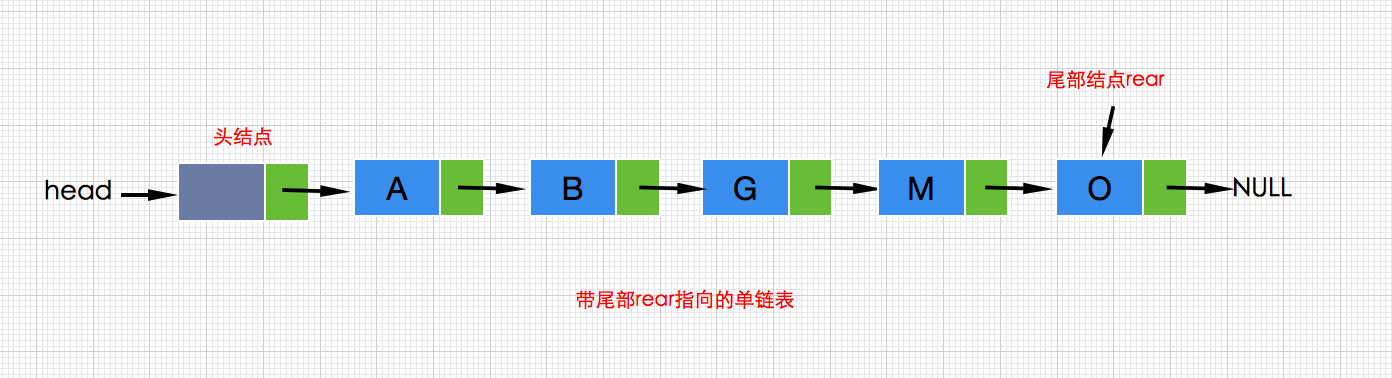
从尾部直接插入的代码实现如下:
/**
* 尾部插入
* @param data
* @return
*/
@Override
public boolean add(T data) {
if (data==null)
throw new NullPointerException("data can\'t be empty!");
this.rear.next = new Node<T>(data);
//更新末尾指针的指向
this.rear = this.rear.next;
return true;
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
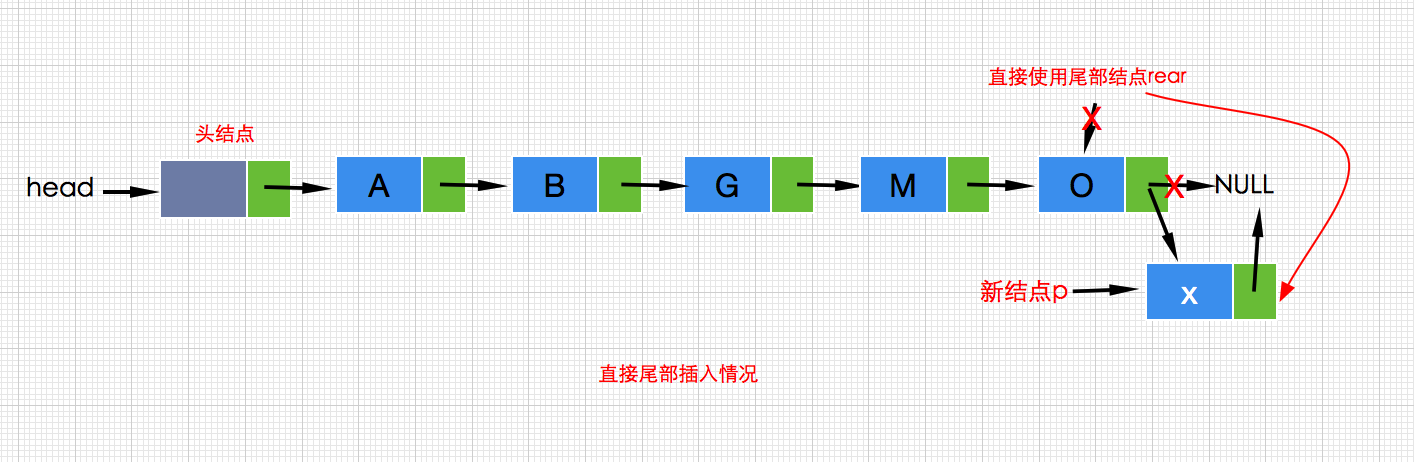
从代码和图示看来确实只要获取当前的尾部指向的结点rear并把新结点赋值给rear.next,最后更新rear结点的值即可,完全不用遍历操作,但是如果是根据index来插入的还,遍历部分结点还是少不了的,下面看看根据index插入的代码实现,由于有了头结点,头部、中间、尾部插入无需区分操作位都视为一种情况处理。
/**
* 根据下标添加结点
* 1.头部插入
* 2.中间插入
* 3.末尾插入
* @param index 该值从0开始,如传4就代表插入在第5个位置
* @param data
* @return
*/
@Override
public boolean add(int index, T data) {
if (data==null){
throw new NullPointerException("data can\'t be empty!");
}
if(index<0)
throw new NullPointerException("index can\'t less than 0");
//无需区分位置操作,中间/头部/尾部插入
int j=0;
Node<T> pre=this.headNode;
//查找到插入位置即index的前一个结点
while (pre.next!=null&&j<index){
pre=pre.next;
j++;
}
//将新插入的结点的后继指针指向pre.next
Node<T> q=new Node<T>(data,pre.next);
//更改指针指向
pre.next=q;
//如果是尾部指针
if (pre==this.rear)
this.rear=q;
return true;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
最后在看看删除的代码实现,由于删除和插入的逻辑和之前不带头结点的单链表分析过的原理的是一样的,因此我们这里不重复了,主要注意遍历的起始结点变化就行。
/**
* 根据索引删除结点
* @param index
* @return
*/
@Override
public T remove(int index) {
T old=null;
//无需区分头删除或中间删除或尾部删除的情况
if (index>=0){
Node<T> pre = this.headNode;
int j = 0;
//查找需要删除位置的前一个结点
while (pre.next != null && j < index) {
pre = pre.next;
j++;
}
//获取到要删除的结点
Node<T> r = pre.next;
if (r != null) {
//获取旧值
old =r.data;
//如果恰好是尾部结点,则更新rear的指向
if (r==this.rear){
this.rear=pre;
}
//更改指针指向
pre.next=r.next;
}
}
return old;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
ok~,关于带头结点的单向链表就分析到这,这里贴出实现源码,同样地,稍后在github上也会提供:
package com.zejian.structures.LinkedList.singleLinked;
import com.zejian.structures.LinkedList.ILinkedList;
/**
* Created by zejian on 2016/10/22.
* 带头结点并含有尾指针的链表
*/
public class HeadSingleILinkedList<T> implements ILinkedList<T> {
protected Node<T> headNode; //不带数据头结点
protected Node<T> rear;//指向尾部的指针
public HeadSingleILinkedList() {
//初始化头结点与尾指针
this.headNode =rear= new Node<>(null);
}
public HeadSingleILinkedList(Node<T> head) {
this();
this.headNode.next =rear.next= head;
rear=rear.next;//更新末尾指针指向
}
/**
* 传入一个数组,转换成链表
* @param array
*/
public HeadSingleILinkedList(T[] array)
{
this();
if (array!=null && array.length>0)
{
this.headNode.next = new Node<T>(array[0]);
rear=this.headNode.next;
int i=1;
while (i<array.length)
{
rear.next=new Node<T>(array[i++]);
rear = rear.next;
}
}
}
/**
* 通过传入的链表构造新的链表
* @param list
*/
public HeadSingleILinkedList(HeadSingleILinkedList<T> list) {
this();
if (list!=null && list.headNode.next!=null)
{
this.headNode.next = new Node(list.headNode.data);
Node<T> p = list.headNode.next;
rear = this.headNode.next;
while (p!=null)
{
rear.next = new Node<T>(p.data);
rear = rear.next;
p = p.next;
}
}
}
/**
* 判断链表是否为空
* @return
*/
@Override
public boolean isEmpty() {
return this.headNode.next==null;
}
@Override
public int length() {
int length=0;
Node<T> currentNode=headNode.next;
while (currentNode!=null){
length++;
currentNode=currentNode.next;
}
return length;
}
/**
* 根据index索引获取值
* @param index 下标值起始值为0
* @return
*/
@Override
public T get(int index) {
if(index>=0){
int j=0;
Node<T> pre=this.headNode.next;
//找到对应索引的结点
while (pre!=null&&j<index){
pre=pre.next;
j++;
}
if(pre!=null){
return pre.data;
}
}
return null;
}
/**
* 根据索引替换对应结点的data
* @param index 下标从0开始
* @param data
* @return 返回旧值
*/
@Override
public T set(int index, T data) {
if(index>=0&&data!=null){
Node<T> pre=this.headNode.next;
int j=0;
while (pre!=null&&j<index){
pre=pre.next;
j++;
}
if (pre!=null){
T oldData=pre.data;
pre.data=data;//设置新值
return oldData;
}
}
return null;
}
/**
* 根据下标添加结点
* 1.头部插入
* 2.中间插入
* 3.末尾插入
* @param index 该值从0开始,如传4就代表插入在第5个位置
* @param data
* @return
*/
@Override
public boolean add(int index, T data) {
if (data==null){
throw new NullPointerException("data can\'t be empty!");
}
if(index<0)
throw new NullPointerException("index can\'t less than 0");
//无需区分位置操作,中间/头部/尾部插入
int j=0;
Node<T> pre=this.headNode;
while (pre.next!=null&&j<index){
pre=pre.next;
j++;
}
//将新插入的结点的后继指针指向pre.next
Node<T> q=new Node<T>(data,pre.next);
//更改指针指向
pre.next=q;
//如果是未指针
if (pre==this.rear)
this.rear=q;
return true;
}
/**
* 尾部插入
* @param data
* @return
*/
@Override
public boolean add(T data) {
if (data==null)
throw new NullPointerException("data can\'t be empty!");
this.rear.next = new Node<T>(data);
//更新末尾指针的指向
this.rear = this.rear.next;
return true;
}
/**
* 根据索引删除结点
* @param index
* @return
*/
@Override
public T remove(int index) {
T old=null;
//包含了头删除或中间删除或尾部删除的情况
if (index>=0){
Node<T> pre = this.headNode;
int j = 0;
//查找需要删除位置的前一个结点
while (pre.next != null && j < index) {
pre = pre.next;
j++;
}
//获取到要删除的结点
Node<T> r = pre.next;
if (r != null) {
//获取旧值
old =r.data;
//如果恰好是尾部结点,则更新rear的指向
if (r==this.rear){
this.rear=pre;
}
//更改指针指向
pre.next=r.next;
}
}
return old;
}
/**
* 根据data移除所有数据相同的结点
* @param data
* @return
*/
@Override
public boolean removeAll(T data) {
boolean isRemove=false;
if(data!=null){
//用于记录要删除结点的前一个结点
Node<T> front=this.headNode;
//当前遍历的结点
Node<T> pre=front.next;
//查找所有数据相同的结点并删除
while (pre!=null){
if(data.equals(pre.data)){
//如果恰好是尾部结点,则更新rear的指向
if(data.equals(rear.data)){
this.rear=front;
}
//相等则删除pre并更改指针指向
front.next=pre.next;
pre =front.next;
isRemove=true;
}else {
front=pre;
pre=pre.next;
}
}
}
return isRemove;
}
/**
* 清空链表
*/
@Override
public void clear() {
this.headNode.next=null;
this.rear=this.headNode;
}
/**
* 判断是否包含某个值
* @param data
* @return
*/
@Override
public boolean contains(T data) {
if(data!=null){
Node<T> pre=this.headNode.next;
while (pre!=null){
if(data.equals(pre.data)){
return true;
}
pre=pre.next;
}
}
return false;
}
/**
* 从末尾连接两个链表
* @param list
*/
public void concat(HeadSingleILinkedList<T> list)
{
if (this.headNode.next==null) {
this.headNode.next = list.headNode.next;
} else {
Node<T> pre=this.headNode.next;
while (pre.next!=null)
pre = pre.next;
pre.next=list.headNode.next;
//更新尾部指针指向
this.rear=list.rear;
}
}
@Override
public String toString() {
String str="(";
Node<T> pre = this.headNode.next;
while (pre!=null)
{
str += pre.data;
pre = pre.next;
if (pre!=null)
str += ", ";
}
return str+")";
}
public static void main(String[] args){
String[] letters={"A","B","C","D","E","F"};
HeadSingleILinkedList<String> list=new HeadSingleILinkedList<>(letters);
System.out.println("list.get(3)->"+list.get(3));
System.out.println("list:"+list.toString());
System.out.println("list.add(4,Y)—>"+list.add(4,"Y"));
System.out.println("list:"+list.toString());
System.out.println("list.add(Z)—>"+list.add("Z"));
System.out.println("list:"+list.toString());
System.out.println("list.contains(Z)->"+list.contains("Z"));
System.out.println("list.set(4,P)-->"+list.set(4,"P"));
System.out.println("list:"+list.toString());
System.out.println("list.remove(Z)->"+list.removeAll("Z"));
System.out.println("list.remove(4)-->"+list.remove(4));
System.out.println("list:"+list.toString());
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 248
- 249
- 250
- 251
- 252
- 253
- 254
- 255
- 256
- 257
- 258
- 259
- 260
- 261
- 262
- 263
- 264
- 265
- 266
- 267
- 268
- 269
- 270
- 271
- 272
- 273
- 274
- 275
- 276
- 277
- 278
- 279
- 280
- 281
- 282
- 283
- 284
- 285
- 286
- 287
- 288
- 289
- 290
- 291
- 292
- 293
- 294
- 295
- 296
- 297
- 298
- 299
- 300
- 301
- 302
- 303
- 304
- 305
- 306
- 307
- 308
- 309
- 310
- 311
- 312
- 313
- 314
- 315
- 316
- 317
- 318
- 319
- 320
- 321
- 322
- 323
- 324
- 325
- 326
- 327
- 328
- 329
- 330
- 331
- 332
- 333
- 334
- 335
- 336
- 337
- 338
- 339
- 340
- 341
- 342
- 343
- 344
- 345
- 346
- 347
- 348
- 349
循环单链表
有上述的分析基础,循环单链表(Circular Single Linked List)相对来说就比较简单了,所谓的循环单链表是指链表中的最后一个结点的next域指向了头结点head,形成环形的结构,我们通过图示来理解:

此时的循环单链表有如下特点:
a.当循环链表为空链表时,head指向头结点,head.next=head。
b.尾部指向rear代表最后一个结点,则有rear.next=head。
在处理循环单链表时,我们只需要注意在遍历循环链表时,避免进入死循环即可,也就是在判断循环链表是否到达结尾时,由之前的如下判断
Node<T> p=this.head;
while(p!=null){
p=p.next;
}- 1
- 2
- 3
- 4
在循环单链表中改为如下判断:
Node<T> p=this.head;
while(p!=this.head){
p=p.next;
}- 1
- 2
- 3
- 4
因此除了判断条件不同,其他操作算法与单链表基本是一样的,下面我们给出循环单链表的代码实现:
package com.zejian.structures.LinkedList.singleLinked;
import com.zejian.structures.LinkedList.ILinkedList;
/**
* Created by zejian on 2016/10/25.
* 循环单链表
*/
public class CircularHeadSILinkedList<T> implements ILinkedList<T> {
protected Node<T> head; //不带数据头结点
protected Node<T> tail;//指向尾部的指针
public CircularHeadSILinkedList() {
//初始化头结点与尾指针
this.head= new Node<T>(null);
this.head.next=head;
this.tail=head;
}
public CircularHeadSILinkedList(T[] array)
{
this();
if (array!=null && array.length>0)
{
this.head.next = new Node<>(array[0],head);
tail=this.head.next;
int i=1;
while (i<array.length)
{
tail.next=new Node<>(array[i++]);
tail.next.next=head;
tail = tail.next;
}
}
}
@Override
public boolean isEmpty() {
return this.head.next==head;
}
@Override
public int length() {
int length=0;
Node<T> p=this.head.next;
while (p!=head){
p=p.next;
length++;
}
return length;
}
@Override
public T get(int index) {
if (index>=0)
{
int j=0;
Node<T> pre=this.head.next;
while (pre!=null && j<index)
{
j++;
pre=pre.next;
}
if (pre!=null)
return pre.data;
}
return null;
}
@Override
public T set(int index, T data) {
if (data==null){
return null;
}
if(index>=0){
int j=0;
Node<T> p=this.head.next;
while (p!=head&&j<index){
j++;
p=p.next;
}
//如果不是头结点
if(p!=head){
T old = p.data;
p.data=data;
return old;
}
}
return null;
}
@Override
public boolean add(int index, T data) {
int size=length();
if(data==null||index<0||index>=size)
return false;
int j=0;
Node<T> p=this.head;
//寻找插入点的位置的前一个结点
while (p.next!=head&&j<index){
p=p.next;
j++;
}
//创建新结点,如果index=3,那么插入的位置就是第4个位置
Node<T> q=new Node<>(data,p.next);
p.next=q;
//更新尾部指向
if(p==tail){
this.tail=q;
}
return true;
}
@Override
public boolean add(T data) {
if(data==null){
return false;
}
Node<T> q=new Node<>(data,this.tail.next);
this.tail.next=q;
//更新尾部指向
this.tail=q;
return true;
}
@Override
public T remove(int index) {
int size=length();
if(index<0||index>=size||isEmpty()){
return null;
}
int j=0;
Node<T> p=this.head.next;
while (p!=head&&j<index){
j++;
p=p.next;
}
if(p!=head){
T old =p.next.data;
if(tail==p.next){
tail=p;
}
p.next=p.next.next;
return old;
}
return null;
}
@Override
public boolean removeAll(T data) {
boolean isRemove=false;
if(data==null){
return isRemove;
}
//用于记录要删除结点的前一个结点
Node<T> front=this.head;
//当前遍历的结点
Node<T> pre=front.next;
//查找所有数据相同的结点并删除
while (pre!=head){
if(data.equals(pre.data)){
//如果恰好是尾部结点,则更新rear的指向
if(data.equals(tail.data)){
this.tail=front;
}
//相等则删除pre并更改指针指向
front.next=pre.next;
pre =front.next;
isRemove=true;
}else {
front=pre;
pre=pre.next;
}
}
return isRemove;
}
@Override
public void clear() {
this.head.next=head;
this.tail=head;
}
@Override
public boolean contains(T data) {
if (data==null){
return false;
}
Node<T> p=this.head.next;
while (p!=head){
if(data.equals(p.data)){
return true;
}
p=p.next;
}
return false;
}
@Override
public String toString()
{
String str="(";
Node<T> p = this.head.next;
while (p!=head)
{
str += p.data.toString();
p = p.next;
if (p!=head)
str += ", ";
}
return str+")";
}
public static void main(String[] args){
String[] letters={"A","B","C","D","E","F"};
CircularHeadSILinkedList<String> list=new CircularHeadSILinkedList<>(letters);
System.out.println("list.get(3)->"+list.get(3));
System.out.println("list:"+list.toString());
System.out.println("list.add(4,Y)—>"+list.add(4,"Y"));
System.out.println("list:"+list.toString());
System.out.println("list.add(Z)—>"+list.add("Z"));
System.out.println("list:"+list.toString());
System.out.println("list.contains(Z)->"+list.contains("Z"));
System.out.println("list.set(4,P)-->"+list.set(4,"P"));
System.out.println("list:"+list.toString());
System.out.println("list.removeAll(Z)->"+list.removeAll("Z"));
System.out.println("list.remove(4)-->"+list.remove(4));
System.out.println("list:"+list.toString());
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 248
- 249
- 250
- 251
- 252
- 253
- 254
- 255
- 256
- 257
- 258
- 259
- 260
- 261
- 262
- 263
- 264
- 265
- 266
3.4 单链表的效率分析
由于单链表并不是随机存取结构,即使单链表在访问第一个结点时花费的时间为常数时间,但是如果需要访问第i(0<i<n)个结点,需要从头结点head开始遍历部分链表,进行i次的p=p.next操作,这点从上述的图文分析我们也可以看出,这种情况类似于前面计算顺序表需要平均移动元素的总数,因此链表也需要平均进行n2次的p=p.next操作,也就是说get(i)和set(i,x)的时间复杂度都为O(n)。
由于链表在插入和删除结点方面十分高效的,因此链表比较适合那些插入删除频繁的场景使用,单纯从插入操作来看,我们假设front指向的是单链表中的一个结点,此时插入front的后继结点所消耗的时间为常数时间O(1),但如果此时需要在front的前面插入一个结点或者删除结点自己时,由于front并没有前驱指针,单凭front根本无法知道前驱结点,所以必须从链表的表头遍历至front的前一个结点再执行插入或者删除操作,而这个查询操作所消耗的时间为O(n),因此在已知front结点需要插入前驱结点或者删除结点自己时,消耗的时间为O(n)。当然这种情况并不是无法解决的,后面我们要分析到的双链表就可以很好解决这个问题,双链表是每个结点都同时拥有前后继结点的链表,这样的话上面的问题就迎刃而解了。上述是从已知单链表中front结点的情况下讨论的单链表的插入删除效率。
我们可能会有个疑问,从前面单链表的插入删除的代码实现上来说,我们并不知道front结点的,每次插入和删除结点,都需要从表头开始遍历至要插入或者删除结点的前一个结点,而这个过程所花费的时间和访问结点所花费的时间是一样的,即O(n),
也就是说从实现上来说确实单链表的插入删除操作花费时间也是O(n),而顺序表插入和删除的时间也是O(n),那为什么说单链表的插入和删除的效率高呢?这里我们要明白的是链表的插入和删除之所以是O(N),是因为查询插入点所消耗的,找到插入点后插入操作消耗时间只为O(1),而顺序表查找插入点的时间为O(1),但要把后面的元素全部后移一位,消耗时间为O(n)。问题是大部分情况下查找所需时间比移动短多了,还有就是链表不需要连续空间也不需要扩容操作,因此即使时间复杂度都是O(n),所以相对来说链表更适合插入删除操作。
以上便是本篇对象顺序表与单链表的分析,如有误处,欢迎留言,我们一起探讨学习。下篇会是双链表的知识点,欢迎持续关注,下面丢出github的地址:
GITHUB博文源码下载地址
关联文章:
java数据结构与算法之顺序表与链表设计与实现分析
java数据结构与算法之双链表设计与实现
java数据结构与算法之改良顺序表与双链表类似ArrayList和LinkedList(带Iterator迭代器与fast-fail机制)
如果您喜欢我写的博文,读后觉得收获很大,不妨小额赞助我一下,让我有动力继续写出高质量的博文,感谢您的赞赏!支付宝、微信