排序算法 | 堆排序，算法的图解、实现、复杂度和稳定性分析_堆排序 稳定性

• 今天讲解一下堆排序的原理以及实现、复杂度和稳定性分析

---

1 堆的定义

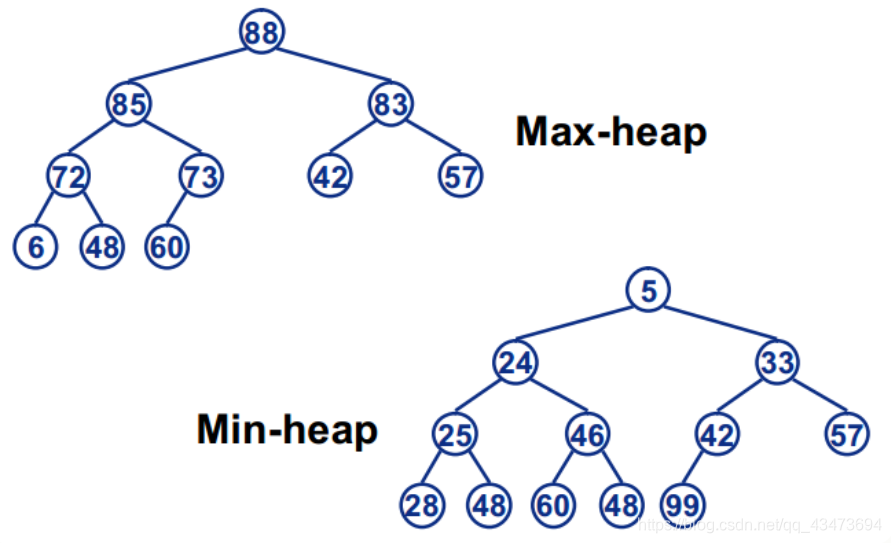
堆排序（英语：Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

定义：
n个关键字序列L[1…n]称为堆，当且仅当该序列满足:

① L(i)>=L(2i) 且 L(i)>=L(2i+1)或

② L(i)<=L(2i) 且 L(i)<=L(2i+1) (1≤isln/2])

可以将该一维数组视为一棵完全二叉树

大根堆：满足条件① 的堆称为大根堆(大顶堆)，大根堆的最大元素存放在根结点，且其任一非根结点的值小于等于其双亲结点值

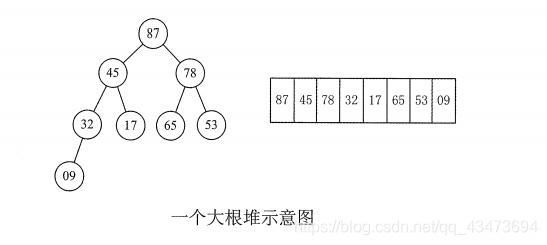
对于堆中的元素编号，其实也是逻辑结构映射到数组的一个过程；

小根堆：满足条件2的堆称为小根堆(小顶堆)，小根堆的定义刚好相反，根结点是最小元素

2 堆排序的思路

首先将存放在L[1…n]中的n个元素建成初始堆，由于堆本身的特点(以大顶堆为例)，堆顶元素就是最大值。
输出堆顶元素后，通常将堆底元素送入堆顶，堆被破坏，将堆顶元素向下调整使其继续保持大顶堆的性质，再输出堆顶元素。如此重复。

• 根据数组构建一个完全二叉树
• 从最后一个非叶节点开始调整，使得子树成为堆
• 如此重复，直至满足堆的定义

值得注意的是：

大根堆排序结果为升序

小根堆排序结果为降序

这是一个常见的误区！

这是因为：堆使用的时候都是每次把堆顶的元素干掉留下