向量的几何意义及编程应用（5）_(cosa -sina sina cosa)的逆矩阵

转载自：http://blog.csdn.net/popy007/article/details/376948

<5>物体的旋转

欢迎回来这里！此次我们要讨论向量的旋转问题，包括平面绕点旋转和空间绕轴旋转两部分。对于游戏程序员来说，有了向量的旋转，就代表有了操纵游戏中物体旋转的钥匙，而不论它是一个平面精灵还是一组空间的网格体亦或是我们放在3-D世界某一点的相机。我们仍需借助向量来完成我们此次的旅程，但这还不够，我们还需要一个朋友，就是矩阵，一个我们用来对向量进行线性变换的GooL GuY。就像我们刚刚提及向量时所做的一样，我们来复习一下即将用到的数学知识。（这部分知识我只会一带而过，因为我将把重点放在后面对旋转问题的分析上）

一、矩阵的基本运算及其性质

对于3x3矩阵(也叫3x3方阵，行列数相等的矩阵也叫方阵）m和M，有

1、矩阵加减法

m +(-) M =

[a b c]      [A B C]   [a+(-)A b+(-)B c+(-)C]
[d e f] +(-) [D E F] = [d+(-)D e+(-)E f+(-)F]
[g h i]      [G H I]   [g+(-)G h+(-)H i+(-)I]

性质：
1）结合律 m + (M + N) = (m + M)  + N
2) 交换律 m + M = M + m

2、数量乘矩阵

k x M =

    [A B C]   [kxA kxB kxC]
k x [D E F] = [kxD kxE kxF]
    [G H I]   [kxG kxH kxI]

性质：

k和l为常数
1) (k + l) x M = k x M + l x M
2) k x (m + M) = k x m + k x M
3) k x (l x M) = (k x l) x M
4) 1 x M = M
5) k x (m x M) = (k x m) x M = m x (k x M)

3、矩阵乘法

m x M =

[a b c]   [A B C}   [axA+bxD+cxG axB+bxE+cxH axC+bxF+cxI]
[d e f] x [D E F] = [dxA+exD+fxG dxB+exE+fxH dxC+exF+fxI]
[g h i]   [G H I]   [gxA+hxD+ixG gxB+hxE+ixH gxC+hxF+ixI]

可以看出，矩阵相乘可以进行的条件是第一个矩阵的列数等于第二个矩阵的行数。
由矩阵乘法的定义看出，矩阵乘法不满足交换率，即在一般情况下，m x M ！= M x m。

性质：
1) 结合律 (m x M) x N = m x (M x N)
2) 乘法加法分配律 m x (M + N) = m x M + m x N ； (m + M) x N = m x N + M x N

4、矩阵的转置
     
m' =
 
[a b c]'   [a d g]
[d e f]  = [b e h] 
[g h i]    [c f i]

性质:
1）(m x M)' = M' x m'
2）(m')' = m
3）(m + M)' = m' + M'
4）(k x M)' = k x M'   

5、单位矩阵
  
    [1 0 0]
E = [0 1 0] 称为3级单位阵
    [0 0 1]

性质：对于任意3级矩阵M，有E x M = M ； M x E = M

6、矩阵的逆

如果3x3级方阵m，有m x M = M x m = E，这里E是3级单位阵，则可以说m是可逆的，它的逆矩阵为M，也记为m^-1。相反的，也可以说M是可逆的，逆矩阵为m，也记为M^-1。

性质：
1) (m^-1)^-1 = m
2) (k x m)^-1 = 1/k x m^-1
3）(m')^-1 = (m^-1)'
4) (m x M)^-1 = M^-1 x n^-1

矩阵求逆有几种算法，这里不深入研究，当我们用到的时候在讨论。
在我们建立了矩阵的概念之后，就可以用它来做坐标的线性变换。好，现在我们开始来使用它。

　

二、基础的2-D绕原点旋转

首先是简单的2-D向量的旋转,以它为基础，我们会深入到复杂的3-D旋转，最后使我们可以在3-D中无所不能的任意旋转。

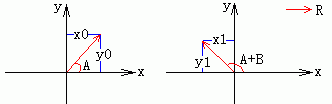
在2-D的迪卡尔坐标系中，一个位置向量的旋转公式可以由三角函数的几何意义推出。比如上图所示是位置向量R逆时针旋转角度B前后的情况。在左图中，我们有关系：

x0 = |R| * cosA
y0 = |R| * sinA
=>
cosA = x0 / |R|
sinA = y0 / |R|

在右图中，我们有关系：

x1 = |R| * cos(A+B)
y1 = |R| * sin(A+B)

其中(x1, y1)就是(x0, y0)旋转角B后得到的点，也就是位置向量R最后指向的点。我们展开cos(A+B)和sin(A+B)，得到

x1 = |R| * (cosAcosB - sinAsinB)
y1 = |R| * (sinAcosB + cosAsinB)

现在把
cosA = x0 / |R|
sinA = y0 / |R|

代入上面的式子，得到

x1 = |R| * (x0 * cosB / |R| - y0 * sinB / |R|)
y1 = |R| * (y0 * cosB / |R| + x0 * sinB / |R|)
=>
x1 = x0 * cosB - y0 * sinB
y1 = x0 * sinB + y0 * cosB

这样我们就得到了2-D迪卡尔坐标下向量围绕圆点的逆时针旋转公式。顺时针旋转就把角度变为负：

x1 = x0 * cos(-B) - y0 * sin(-B)
y1 = x0 * sin(-B) + y0 * cos(-B)
=>
x1 = x0 * cosB + y0 * sinB
y1 = -x0 * sinB + y0 * cosB

现在我要把这个旋转公式写成矩阵的形式，有一个概念我简单提一下，平面或空间里的每个线性变换（这里就是旋转变换）都对应一个矩阵，叫做变换矩阵。对一个点实施线性变换就是通过乘上该线性变换的矩阵完成的。好了，打住，不然就跑题了。

所以2-D旋转变换矩阵就是:

[cosA  sinA]      [cosA -sinA]
[-sinA cosA] 或者 [sinA cosA]

我们对点进行旋转变换可以通过矩阵完成，比如我要点(x, y)绕原点逆时针旋转：

          [cosA  sinA]  
[x, y] x  [-sinA cosA] = [x*cosA-y*sinA  x*sinA+y*cosA]

为了编程方便，我们把它写成两个方阵

[x, y]   [cosA  sinA]   [x*cosA-y*sinA  x*sinA+y*cosA]
[0, 0] x [-sinA cosA] = [0              0            ]

也可以写成

[cosA -sinA]   [x 0]   [x*cosA-y*sinA  0]
[sinA  cosA] x [y 0] = [x*sinA+y*cosA  0]

三、2-D的绕任一点旋转

下面我们深入一些，思考另一种情况：求一个点围绕任一个非原点的中心点旋转。

我们刚刚导出的公式是围绕原点旋转的公式，所以我们要想继续使用它，就要把想要围绕的那个非原点的中心点移动到原点上来。按照这个思路，我们先将该中心点通过一个位移向量移动到原点，而围绕点要保持与中心点相对位置不变，也相应的按照这个位移向量位移，此时由于中心点已经移动到了圆点，就可以让同样位移后的围绕点使用上面的公式来计算旋转后的位置了，计算完后，再让计算出的点按刚才的位移向量 逆 位移，就得到围绕点绕中心点旋转一定角度后的新位置了。看下面的图

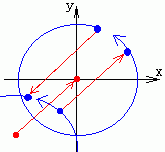
现在求左下方的蓝色点围绕红色点旋转一定角度后的新位置。由于红色点不在原点，所以可以通过红色向量把它移动到原点，此时蓝色的点也按照这个向量移动，可见，红色和蓝色点的相对位置没有变。现在红色点在原点，蓝色点可以用上面旋转变换矩阵进行旋转，旋转后的点在通过红色向量的的逆向量回到它实际围绕下方红色点旋转后的位置。

在这个过程中，我们对围绕点进行了三次线性变换：位移变换-旋转变换-位移变换，我们把它写成矩阵形式：

设红色向量为(rtx, rty)

[x y 1]   [1   0   0]   [cosA  sinA 0]   [1    0    0]   [x' y' -]
[0 1 0] x [0   1   0] x [-sinA cosA 0] x [0    1    0] = [-  -  -]
[0 0 1]   [rtx rty 1]   [0     0    1]   [-rtx -rty 1]   [-  -  -]

最后得到的矩阵的x'和y'就是我们旋转后的点坐标。

注意到矩阵乘法满足结合律：(m x M) x N = m x (M x N)，我们可以先将所有的变换矩阵乘在一起，即

    [1   0   0]   [cosA  sinA 0]   [1    0    0] 
M = [0   1   0] x [-sinA cosA 0] x [0    1    0]  
    [rtx rty 1]   [0     0    1]   [-rtx -rty 1]  

然后再让

[x y 1]
[0 1 0] x M
[0 0 1]

像这样归并变换矩阵是矩阵运算一个常用的方法，因为当把诸多变换矩阵归并为一个矩阵之后，对某点或向量的重复变换只需要乘一个矩阵就可以完成，减少了计算的开销。

本小节讨论的这种“其他变换-绕点旋转变换-其他变换”的思想很重要，因为有时候复杂一些的旋转变换不可能一步完成，必须使用这种旁敲侧击、化繁为简的方法，尤其是在3-D空间中，可能需要在真正做规定度数的旋转前还要做一些其他必要旋转变换，也就是要做很多次的旋转，但总体的思想还是为了把复杂的问题分成若干简单的问题去解决，而每一个简单问题都需要一个变换矩阵来完成，所以希望读者深入思考一下这种方法。

好，2-D的旋转探讨完毕。接下来，我们进入3-D空间，讨论更为复杂一些的旋转。Here We Go!

　
四、基础的3-D绕坐标轴方向旋转

就像2-D绕原点旋转一样，3-D的绕坐标轴旋转是3-D旋转的基础，因为其他复杂的3-D旋转最后都会化简为绕坐标轴旋转。其实，刚才我们推导出的在xoy坐标面绕o旋转的公式可以很容易的推广到3-D空间中，因为在3-D直角坐标系中，三个坐标轴两两正交，所以z轴垂直于xoy面，这样，在xoy面绕o点旋转实际上在3-D空间中就是围绕z轴旋转，如下图左所示：

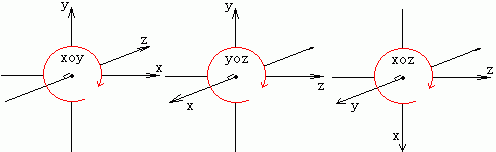
这张图描述了左手系中某点在xoy、yoz、xoz面上围绕原点旋转的情况，同时也是分别围绕z、x、y坐标轴旋转。可见在3-D空间中绕坐标轴旋转相当于在相应的2-D平面中围绕原点旋转。我们用矩阵来说明：

设p(x, y, z）是3-D空间中的一点，也可以说是一个位置向量，当以上图中的坐标为准，p点所围绕的中心轴指向你的屏幕之外时，有

p绕z轴逆时针和顺时针旋转角度A分别写成：

[x y z 1]   [cosA -sinA 0 0]    [x y z 1]   [cosA sinA  0 0]
[0 1 0 0] x [sinA cosA  0 0] 和 [0 1 0 0] x [-sinA cosA 0 0] 
[0 0 1 0]   [0    0     1 0]    [0 0 1 0]   [0     0    1 0]
[0 0 0 1]   [0    0     0 1]    [0 0 0 1]   [0     0    0 1]

p绕x轴逆时针和顺时针旋转角度A分别写成：

[x y z 1]   [1 0     0    0]    [x y z 1]   [1 0     0    0]
[0 1 0 0] x [0 cos  -sinA 0] 和 [0 1 0 0] x [0 cosA  sinA 0] 
[0 0 1 0]   [0 sin  cosA  0]    [0 0 1 0]   [0 -sinA cosA 0]
[0 0 0 1]   [0 0    0     1]    [0 0 0 1]   [0 0     0    1]

p绕y轴逆时针和顺时针旋转角度A分别写成：

[x y z 1]   [cosA  0 sinA 0]    [x y z 1]   [cosA 0  -sinA 0]
[0 1 0 0] x [0     1 0    0] 和 [0 1 0 0] x [0     1  0    0] 
[0 0 1 0]   [-sinA 0 cosA 0]    [0 0 1 0]   [sinA  0  cosA 0]
[0 0 0 1]   [0     0 0    1]    [0 0 0 1]   [0     0  0    1]

以后我们会把它们写成这样的标准4x4方阵形式，Why？为了便于做平移变换，还记得上小节做平移时我们把2x2方阵写为3x3方阵吗？

让我们继续研究。我们再把结论推广一点，让它适用于所有和坐标轴平行的轴，具体一点，让它适用于所有和y轴平行的轴。
这个我们很快可以想到，可以按照2-D的方法“平移变换-旋转变换-平移变换”来做到，看下图

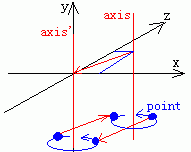
要实现point绕axis旋转，我们把axis按照一个位移向量移动到和y轴重合的位置，也就是变换为axis'，为了保持point和axis的相对位置不变,point也通过相同的位移向量做相应的位移。好，现在移动后的point就可以用上面的旋转矩阵围绕axis'也就是y轴旋转了，旋转后用相反的位移向量位移到实际围绕axis相应度数的位置。我们还是用矩阵来说明：

假设axis为x = s, z = t，要point(x, y, z)围绕它逆时针旋转度数A，按照“平移变换-旋转变换-位移变换”，我们有

[x y z 1]   [1  0 0  0]   [cosA  0 sinA 0]   [1 0 0 0]   [x' y z' -]
[0 1 0 0]   [0  1 0  0]   [0     1 0    0]   [0 1 0 0]   [-  - -  -]
[0 0 1 0] x [0  0 1  0] x [-sinA 0 cosA 0] x [0 0 1 0] = [-  - -  -]
[0 0 0 1]   [-s 0 -t 1]   [0     0 0    1]   [s 0 t 1]   [-  - -  -]

则得到的(x', y, z')就是point围绕axis旋转角A后的位置。

同理，平行于x轴且围绕轴y=s,z=t逆时针旋转角A的变换为

[x y z 1]   [1  0 0  0]   [1 0    0     0]   [1 0 0 0]   [x  y' z' -]
[0 1 0 0]   [0  1 0  0]   [0 cosA -sinA 0]   [0 1 0 0]   [-  -  -  -]
[0 0 1 0] x [0  0 1  0] x [0 sinA cosA  0] x [0 0 1 0] = [-  -  -  -]
[0 0 0 1]   [0 -s -t 1]   [0 0    0     1]   [0 s t 1]   [-  -  -  -]

平行于z轴且围绕轴x=s,y=t逆时针旋转角A的变换为

[x y z 1]   [1  0  0  0]   [cosA -sinA 0 0]   [1 0 0 0]   [x' y' z  -]
[0 1 0 0]   [0  1  0  0]   [sinA cosA  0 0]   [0 1 0 0]   [-  -  -  -]
[0 0 1 0] x [0  0  1  0] x [0    0     1 0] x [0 0 1 0] = [-  -  -  -]
[0 0 0 1]   [-s -t 0  1]   [0    0     0 1]   [s t 0 1]   [-  -  -  -]

逆时针旋转就把上面推出的相应逆时针旋转变换矩阵带入即可。至此我们已经讨论了3-D空间基本旋转的全部，接下来的一小节是我们3-D旋转部分的重头戏，也是3-D中功能最强大的旋转变换。

五、3-D绕任意轴的旋转

Wow!终于来到了最后一部分，这一节我们将综合运用上面涉及到的所有旋转知识，完成空间一点或着说位置向量围绕空间任意方向旋转轴的旋转变换（我在下面介绍的一种方法是一个稍微繁琐一点的方法，大体上看是利用几个基本旋转的综合。我将在下一篇中介绍一个高档一些的方法）。

何谓任意方向的旋转轴呢？其实就是空间一条直线。在空间解析几何中，决定空间直线位置的两个值是直线上一点以及直线的方向向量。在旋转中，我们把这个直线称为一个旋转轴，因此，直线的这个方向向量我们叫它轴向量，它类似于3-D动画中四元数的轴向量。我们在实际旋转之前的变换矩阵需要通过把这个轴向量移动到原点来获得。


我们先讨论旋转轴通过原点的情况。目前为止对于3-D空间中的旋转，我们可以做的只是绕坐标轴方向的旋转。因此，当我们考虑非坐标轴方向旋转的时候，很自然的想到，可以将这个旋转轴通过变换与某一个坐标轴重合，同时，为了保持旋转点和这个旋转轴相对位置不变，旋转点也做相应的变换，然后，让旋转点围绕相应旋转轴重合的坐标轴旋转，最后将旋转后的点以及旋转轴逆变换回原来的位置，此时就完成了一点围绕这个非坐标轴方向旋转轴的旋转。我们再来看图分析。

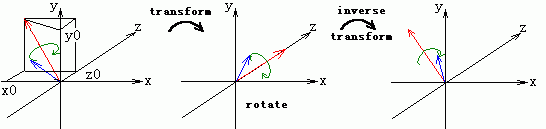
图中有一个红色的分量为(x0, y0, z0)的轴向量，此外有一个蓝色位置向量围绕它旋转，由于这个轴向量没有与任何一个坐标轴平行，我们没有办法使用上面推导出的旋转变换矩阵，因此必须将该轴变换到一个坐标轴上，这里我们选择了z轴。在变换红色轴的同时，为了保持蓝色位置向量同该轴的相对位置不变，也做相应的变换，然后就出现中图描述的情况。接着我们就用可以用变换矩阵来围绕z轴旋转蓝色向量相应的度数。旋转完毕后，再用刚才变换的逆变换把两个向量相对位置不变地还原到初始位置，此时就完成了一个点围绕任意过原点的轴的旋转，对于不过原点的轴我们仍然用“位移变换-旋转变换-位移变换”的方法，一会讨论。

在理解了基本思路之后，我们来研究一下变换吧！我们就按上图将红色轴变到z轴上，开始吧！

首先我们假设红轴向量是一个单位向量，因为这样在一会求sin和cos时可以简化计算，在实际编程时可以先将轴向量标准化。然后我准备分两步把红色轴变换到z轴上去:

1）将红色轴变换到yoz平面上
2) 将yoz平面上的红色轴变到z轴上

至于这两个变换的方法...我实在没有别的办法了，只能够旋转了，你觉得呢？先把它旋转到yoz平面上。

我们设轴向量旋转到yoz面的变换为（绕z轴旋转）：

[cosA  sinA 0 0]
[-sinA cosA 0 0]
[0     0    1 0]
[0     0    0 1] 

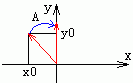
接着我们要求出cosA和sinA，由上图，沿着z轴方向看去，我们看到旋转轴向量到yoz面在xoy面就是将轴的投影向量旋转角度A到y轴上，现在我不知道角度A，但是我们可以利用它直接求出cosA和sinA，因为我们知道关系：

cosA = y0 / 轴向量在xoy面的投影长
sinA = x0 / 轴向量在xoy面的投影长

我们设轴向量的投影长为lr = sqrt(x0^2 + y0^2)，呵呵，现在，我们第一步的变换矩阵就出来了：

[y0/lr  x0/lr 0 0]
[-x0/lr y0/lr 0 0]
[0      0     1 0]
[0      0     0 1]

同时我们得到逆变换矩阵：

[y0/lr -x0/lr 0 0]
[x0/lr y0/lr  0 0]
[0      0     1 0]
[0      0     0 1]

然后我们进行第二步：将yoz平面上的红色轴变到z轴上。我们的变换矩阵是（绕x轴旋转）：

[1 0     0    0]
[0 cosB  sinB 0]
[0 -sinB cosB 0]
[0 0     0    1]

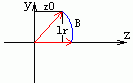
由图，这是经第一次旋转后的轴向量在yoz面中的情形，此次我们要求出上面变换中的cosB和sinB，我们仍不知道角度B，但我们还是可以利用它求cosB和sinB。由于第一次旋转是围绕z轴，所以轴向量的z分量没有变，还是z0。此外，轴向量现在的y分量和原来不同了，我们再看一下第一次变换那张图，可以发现轴向量在旋转到yoz面后，y分量变成了刚才轴向量在xoy面上的投影长lr了。Yes！我想是时候写出cosB和sinB了：

cosB = z0 / 轴向量的长
sinB = lr / 轴向量的长

还记得我们刚才假设轴向量是一个单位向量吗？所以

cosB = z0
sinB = lr

至此我们的第二个变换就出来了：

[1 0   0   0]
[0 z0  lr  0]
[0 -lr z0  0]
[0 0   0   1]

相应逆变换矩阵：

[1 0   0   0]
[0 z0  -lr 0]
[0 lr  z0  0]
[0 0   0   1]

现在总结一下，我们对于空间任意点围绕某个任意方向且过原点的轴旋转的变换矩阵就是：



    [y0/lr  x0/lr 0 0]   [1 0   0  0]   [cosA  sinA 0 0]   [1 0  0   0]   [y0/lr  -x0/lr 0 0]
    [-x0/lr y0/lr 0 0]   [0 z0  lr 0]   [-sinA cosA 0 0]   [0 z0 -lr 0]   [x0/lr  y0/lr  0 0]
M = [0      0     1 0] x [0 -lr z0 0] x [0     0    1 0] x [0 lr z0  0] x [0      0      1 0]
    [0      0     0 1]   [0 0   0  1]   [0     0    0 1]   [0 0  0   1]   [0      0      0 1]

上面的变换是“旋转变换-旋转变换-旋转变换-旋转变换-旋转变换”的变换组。当我们需要让空间中的某个位置向量围绕一个轴旋转角度A的时候，就可以用这个向量相应的矩阵乘上这个M，比如

[x y 0 0]       [x' y' z' -]
[0 1 0 0]       [-  -  -  -]
[0 0 1 0] x M = [-  -  -  -] 
[0 0 0 1]       [-  -  -  -]

当然，M中矩阵相应的元素是根据轴向量得到的。

以上的变换矩阵是通过把轴向量变到z轴上得到的，而且是先旋转到yoz面上，然后再旋转到z轴上。我们也可以不这样做，而是先把轴向量旋转到xoz面上，然后再旋转到z轴上。此外，我们还可以把轴向量变到x或y轴上，这一点我们可以自己决定。虽然变换不同，但推导的道理是相同的，都是这种“其他变换-实际旋转变换-其他变换”的渗透形式。

刚才分析的是旋转轴过原点的情况，对于一般的旋转轴，虽然我们也都是把它的轴向量放到原点来考虑，但我们不能只是让旋转点围绕过原点的轴向量旋转完就算完事，我们仍需要采用“平移变换-旋转变换-平移变换”方法。即先将旋转轴平移到过原点方向，旋转点也做相应平移，接着按上面推出的变换阵旋转，最后将旋转轴和点逆平移回去。这里，我们只需在M的左右两边各加上一个平移变换即可。这个平移变换的元素是根据轴向量与原点之间的距离向量得到的，比如旋转轴与原点的距离向量是(lx, ly, lz)，则我们的变换就变成


    [1   0    0  0]       [1  0  0  0]
    [0   1    0  0]       [0  1  0  0]
m = [0   0    1  0] x M x [0  0  1  0]
    [-lx -ly -lz 1]       [lx ly lz 1]

变换矩阵m就是全部7个变换矩阵的归并，适用于各种旋转情况。

我们现在已经讨论完了一般的2-D、3-D旋转了。可以看出其基本的思想还是能够化繁为简的变换、归并。而实际的旋转也仍是用我们最最基本的2-D绕原点旋转公式。其实还有很多的旋转效果可以用我们上面的变换、公式稍加修改获得。比如螺旋形旋转、旋转加前进、随机旋转等等。下一篇将介绍一个用的最多的高档一些的方法，下次见。