利用随机森林对特征重要性进行评估 方法一_可变重要性度量vim

https://hal.archives-ouvertes.fr/file/index/docid/755489/filename/PRLv4.pdf

前言

随机森林是以决策树为基学习器的集成学习算法。随机森林非常简单，易于实现，计算开销也很小，更令人惊奇的是它在分类和回归上表现出了十分惊人的性能，因此，随机森林也被誉为“代表集成学习技术水平的方法”。 
本文是对随机森林如何用在特征选择上做一个简单的介绍。

随机森林（RF）简介

只要了解决策树的算法，那么随机森林是相当容易理解的。随机森林的算法可以用如下几个步骤概括：

1. 用有抽样放回的方法（bootstrap）从样本集中选取n个样本作为一个训练集
2. 用抽样得到的样本集生成一棵决策树。在生成的每一个结点： 
   • 随机不重复地选择d个特征
   • 利用这d个特征分别对样本集进行划分，找到最佳的划分特征（可用基尼系数、增益率或者信息增益判别）
3. 重复步骤1到步骤2共k次，k即为随机森林中决策树的个数。
4. 用训练得到的随机森林对测试样本进行预测，并用票选法决定预测的结果。

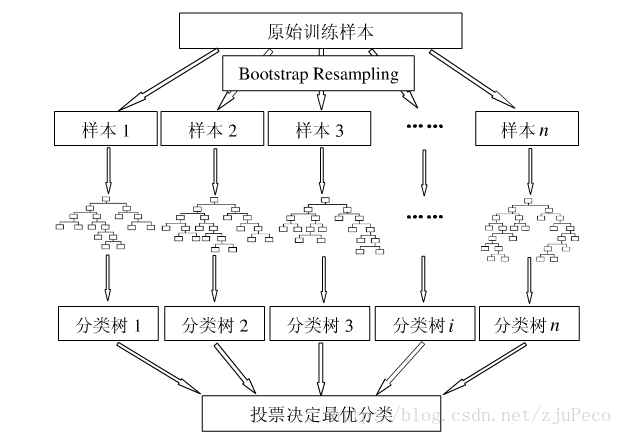
下图比较直观地展示了随机森林算法（图片出自文献2）： 

 

图1：随机森林算法示意图

没错，就是这个到处都是随机取值的算法，在分类和回归上有着极佳的效果，是不是觉得强的没法解释~ 
然而本文的重点不是这个，而是接下来的特征重要性评估。

 

特征重要性评估

现实情况下，一个数据集中往往有成百上前个特征，如何在其中选择比结果影响最大的那几个特征，以此来缩减建立模型时的特征数是我们比较关心的问题。这样的方法其实很多，比如主成分分析，lasso等等。不过，这里我们要介绍的是用随机森林来对进行特征筛选。 
用随机森林进行特征重要性评估的思想其实很简单，说白了就是看看每个特征在随机森林中的每颗树上做了多大的贡献，然后取个平均值，最后比一比特征之间的贡献大小。 
好了，那么这个贡献是怎么一个说法呢？通常可以用基尼指数（Gini index）或者袋外数据（OOB）错误率作为评价指标来衡量。 
我们这里只介绍用基尼指数来评价的方法，想了解另一种方法的可以参考文献2。 
我们将变量重要性评分（variable importance measures）用VIMVIM来表示，将Gini指数用GIGI来表示，假设有mm个特征X1，X2，X3，...，XcX1，X2，X3，...，Xc，现在要计算出每个特征XjXj的Gini指数评分VIM(Gini)jVIMj(Gini)，亦即第jj个特征在RF所有决策树中节点分裂不纯度的平均改变量。 
Gini指数的计算公式为 

GIm=∑|K|k=1∑k′≠kpmkpmk′=1−∑|K|k=1p2mkGIm=∑k=1|K|∑k′≠kpmkpmk′=1−∑k=1|K|pmk2

其中，KK表示有KK个类别，pmkpmk表示节点mm中类别kk所占的比例。 
直观地说，就是随便从节点mm中随机抽取两个样本，其类别标记不一致的概率。 
特征XjXj在节点mm的重要性，即节点mm分枝前后的GiniGini指数变化量为 

VIM(Gini)jm=GIm−GIl−GIrVIMjm(Gini)=GIm−GIl−GIr

其中，GIlGIl和GIrGIr分别表示分枝后两个新节点的GiniGini指数。 
如果，特征XjXj在决策树ii中出现的节点在集合MM中，那么XjXj在第ii颗树的重要性为 

VIM(Gini)ij=∑m∈MVIM(Gini)jmVIMij(Gini)=∑m∈MVIMjm(Gini)

假设RFRF中共有nn颗树，那么 

VIM(Gini)j=∑ni=1VIM(Gini)ijVIMj(Gini)=∑i=1nVIMij(Gini)

最后，把所有求得的重要性评分做一个归一化处理即可。 

VIMj=VIMj∑ci=1VIMiVIMj=VIMj∑i=1cVIMi

 

举个例子

值得庆幸的是，sklearnsklearn已经帮我们封装好了一切，我们只需要调用其中的函数即可。 
我们以UCI上葡萄酒的例子为例，首先导入数据集。

import pandas as pd
url = 'http://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data'
df = pd.read_csv(url, header = None)
df.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash', 
              'Alcalinity of ash', 'Magnesium', 'Total phenols', 
              'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins', 
              'Color intensity', 'Hue', 'OD280/OD315 of diluted wines', 'Proline']

• 1
• 2
• 3
• 4
• 5
• 6
• 7

然后，我们来大致看下这时一个怎么样的数据集

import numpy as np
np.unique(df['Class label'])

• 1
• 2

输出为

array([1, 2, 3], dtype=int64)

• 1

可见共有3个类别。然后再来看下数据的信息：

df.info()

• 1

输出为

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 178 entries, 0 to 177
Data columns (total 14 columns):
Class label                     178 non-null int64
Alcohol                         178 non-null float64
Malic acid                      178 non-null float64
Ash                             178 non-null float64
Alcalinity of ash               178 non-null float64
Magnesium                       178 non-null int64
Total phenols                   178 non-null float64
Flavanoids                      178 non-null float64
Nonflavanoid phenols            178 non-null float64
Proanthocyanins                 178 non-null float64
Color intensity                 178 non-null float64
Hue                             178 non-null float64
OD280/OD315 of diluted wines    178 non-null float64
Proline                         178 non-null int64
dtypes: float64(11), int64(3)
memory usage: 19.5 KB

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19

可见除去class label之外共有13个特征，数据集的大小为178。 
按照常规做法，将数据集分为训练集和测试集。

from sklearn.cross_validation import train_test_split
from sklearn.ensemble import RandomForestClassifier
x, y = df.iloc[:, 1:].values, df.iloc[:, 0].values
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3, random_state = 0)
feat_labels = df.columns[1:]
forest = RandomForestClassifier(n_estimators=10000, random_state=0, n_jobs=-1)
forest.fit(x_train, y_train)

• 1
• 2
• 3
• 4
• 5
• 6
• 7

好了，这样一来随机森林就训练好了，其中已经把特征的重要性评估也做好了，我们拿出来看下。

importances = forest.feature_importances_
indices = np.argsort(importances)[::-1]
for f in range(x_train.shape[1]):
    print("%2d) %-*s %f" % (f + 1, 30, feat_labels[indices[f]], importances[indices[f]]))

• 1
• 2
• 3
• 4

输出的结果为

 1) Color intensity                0.182483
 2) Proline                        0.158610
 3) Flavanoids                     0.150948
 4) OD280/OD315 of diluted wines   0.131987
 5) Alcohol                        0.106589
 6) Hue                            0.078243
 7) Total phenols                  0.060718
 8) Alcalinity of ash              0.032033
 9) Malic acid                     0.025400
10) Proanthocyanins                0.022351
11) Magnesium                      0.022078
12) Nonflavanoid phenols           0.014645
13) Ash                            0.013916

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13

对的就是这么方便。 
如果要筛选出重要性比较高的变量的话，这么做就可以

threshold = 0.15
x_selected = x_train[:, importances > threshold]
x_selected.shape

• 1
• 2
• 3

输出为

(124, 3)

• 1

瞧，这不，帮我们选好了3个重要性大于0.15的特征了吗~

参考文献

[1] Raschka S. Python Machine Learning[M]. Packt Publishing, 2015. 
[2] 杨凯, 侯艳, 李康. 随机森林变量重要性评分及其研究进展[J]. 2015.