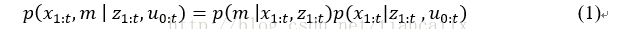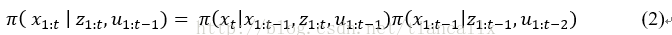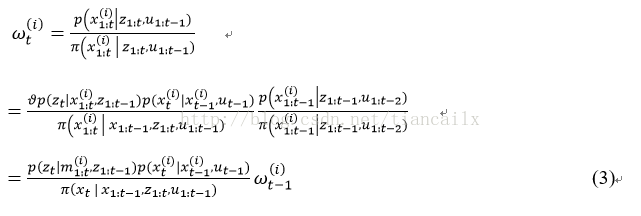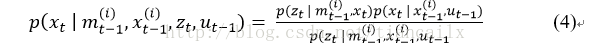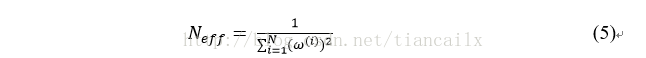基于粒子滤波的SLAM(GMapping)算法分析_gmapping优化

本文是《Improved Techniques for Grid Mapping_with Rao-Blackwellized Particle Filters》的大致翻译，难免有不通顺与错误的地方，如有错误请指出，谢谢！
 
设想一个机器人在一个未知环境中移动，其目的是获得当前环境的地图。地图可以用一个储存每个网格单元颜色的矩阵表示，单元格的颜色只能为黑色或白色。由于传感器与电机都存在误差，运动很可能偏离目标方向，因此机器人很容易“迷路”。所以同步定位与地图构建(SLAM)问题总是被称作“鸡和蛋”的问题：机器人首先需要知道自身的位置去获得一个准确的地图，但是获取地图同样也需要一个准确的定位。定位与地图估计之间的相互依赖使SLAM问题变得非常困难，并且通常需要在高维空间中搜索解决方案。
很多学者对SLAM问题进行了广泛的研究。在2000年，Murphy应用Rao-Blackwellized粒子滤波算法去解决SLAM问题。Rao-Blackwellized的主要方式是用许多粒子去获取准确的地图。因此减少粒子的数量是优化这一算法的主要挑战。

1 地图构建中的Rao-Blackwellized粒子滤波算法

SLAM的核心思想是根据其观测值和其里程计测量信息去估计联合后验概率密度函数（代表地图中的点、代表机器人的轨迹）。可以看出，轨迹和地图需要同时计算出来，这样的计算很复杂而且计算的结果可能不收敛。而RBPF(Rao-Blackwellized Particle Filter)算法利用公式(1)对联合概率密度函数进行因式分解。

因此RBPF可以先估计机器人的轨迹而后再去根据已知的轨迹计算地图。由地图的概率密度函数可以看出，地图强烈依赖于机器人的位姿，所以这个方法是可行的。
地图的概率密度函数可以通过已知位姿的建图方法“mapping with known poses”来计算。后验概率密度函数应用粒子滤波来估计。
粒子滤波算法的核心思想是利用一系列随机样本的加权和近似后验概率密度函数，通过求和来近似积分操作。该算法源于Monte Carlo思想，即以某事件出现的频率来指代该事件的概率。因此在滤波过程中，需要用到概率的地方，一概对变量采样，以大量采样及其相应的权值来近似表示概率密度函数。
其中最普遍的粒子滤波算法为SIR(Samping Importance Resampling)滤波器。该算法通过以下四步完成：

1）预测阶段：粒子滤波首先根据状态转移函数预测生成大量的采样，这些采样就称之为粒子，利用这些粒子的加权和来逼近后验概率密度。
2）校正阶段：随着观测值的依次到达，为每个粒子计算相应的重要性权值。这个权值代表了预测的位姿取第个粒子时获得观测的概率。如此这般下来，对所有粒子都进行这样一个评价，越有可能获得观测的粒子，获得的权重越高。
3）重采样阶段：根据权值的比例重新分布采样粒子。由于近似逼近连续分布的粒子数量有限，因此这个步骤非常重要。下一轮滤波中，再将重采样过后的粒子集输入到状态转移方程中，就能够获得新的预测粒子了。
4）地图估计：对于每个采样的粒子，通过其采样的轨迹与观测计算出相应的地图估计。
SIR算法需要在新的观测值到达时从头评估粒子的权重。当轨迹的长度随着时间的推移而增加时，这个过程的计算复杂度将越来越高。因此Doucet等学者通过式(2)限制重要性概率密度函数来获得递归公式去计算重要性权值。

根据等式2，权值可通过以下公式计算

 

2 GMapping中的优化算法

GMapping为2007年在ROS中开源的SLAM软件包，是目前使用最广泛的软件包。它可用于室内和室外，应用改进的自适应RBPF算法来进行定位与建图。
Doucet等学者基于RBPF算法提出了改进的重要性概率密度函数并且增加了自适应重采样技术。如上一节所述，为了获得下一迭代步骤的粒子采样我们需要在预测阶段从重要性概率密度函数中抽取样本。显然，重要性概率密度函数越接近目标分布，滤波器的效果越好。

 

 

2.1 最优重要性概率密度函数

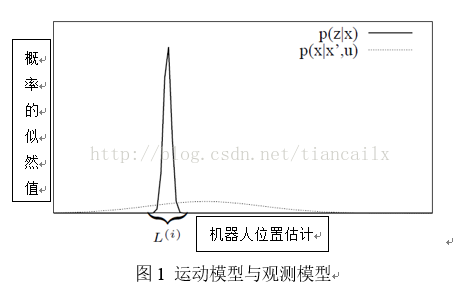
典型的粒子滤波器应用里程计运动模型作为重要性概率密度函数。这种运动模型的计算非常简单，并且权值只根据观测模型即可算出。然而，这种模型并不是最理想的。当机器人装备激光雷达（如SICK，Hokuyo等）时，激光测得的数据比里程计精确的多，因此使用观测模型作为重要性概率密度函数将要准确的多。图1展示了观测模型的分布明显小于运动模型的分布。由于观测模型的分布区域很小，样本处在观测的分布（图中的区域）的几率很小，在保证充分覆盖观测的分布情况下所需要的粒子数就会变得很多，这将会导致使用运动模型作为重要性概率密度函数类似的问题：需要大量的样本来充分覆盖分布的区域。


为了克服这个问题，可以在生成下一次采用时将最近的观测考虑进去。通过将整合到概率分布中，可以将抽样集中在观测似然的有意义的区域。为此Doucet等提出了最优重要性概率密度函数，式4为粒子权重方差的最优分布。

所以式(4)在机器人装备激光测距仪的时候非常适用。
现在的RBPF算法过程是这样的，首先根据运动模型对机器人下一时刻位姿进行预测，得到预测的状态值并且对其进行采样。第二步是通过最优概率密度函数（4）对各个粒子进行权值的计算。之后进行重采样，根据粒子的权重重新分布粒子，为下次预测提供输入。最后，根据粒子的轨迹计算地图的后验概率密度函数。


图2中展示了在不同场景下的粒子分布情况。（a）为在开放的走廊中，粒子沿着走廊分布。（b）为在死胡同中，粒子分布的不确定性很小，分布的很集中。（c）为根据里程计运动模型预测生成的粒子分布，分布的很分散。
因此，该算法将最近的里程计信息与观测信息同时并入重要性概率密度函数中，使用匹配扫描过程来确定观察似然函数的分布区域，这样就把采样的重点集中在可能性更高的区域。当由于观察不佳或者当前扫描与先前计算的地图重叠区域太小而失败时，将会用图2中（c）所示的里程计运动模型作为重要性概率密度函数。

 

 

2.2 自适应重采样

对粒子滤波的性能具有重要影响的另一个因素是重采样步骤。在重采样期间，低权值的粒子通常由高权值的采样代替。由于用来逼近目标分布使用的粒子数量是有限的，所以重采样步骤非常重要。重采样步骤也可能把一些好的粒子滤去，随着的进行，粒子的数目会逐渐减少，最后导致粒子耗尽使该算法失效。通常采用有效粒子数来衡量粒子权值的退化程度，即

这里的为粒子的归一化权值。
Doucet等为了减少进行重采样步骤的次数，提出了一种理论判定方法来判定是否需要进行重采样。只有当下降到阈值（，为粒子数）以下时，才进行一次重采样。由于重采样只在需要时进行，进行重采样的次数将大大减少。多次的实验证明了这种方法大大降低了将好粒子滤去的风险。

 

 

3 实验

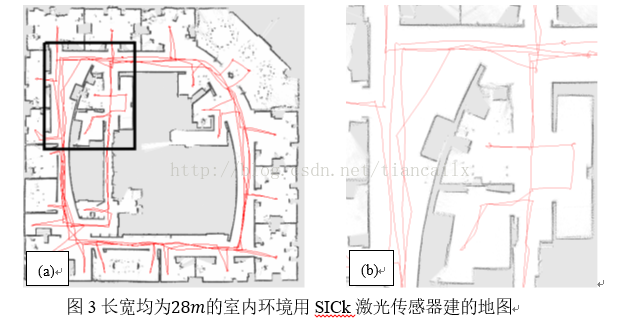
图3的(a)图是通过配有SICK激光传感器的先锋2(Pioneer 2)机器人在长宽均为28m的室内环境中构建的地图。图3的(b)图显示了该地图的放大细节，展示了该算法建图的准确性。


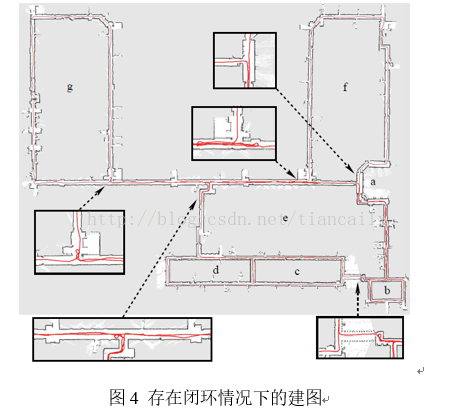
图4显示了包含几个嵌套闭环的室内环境。在这种环境下地图构建非常困难，闭环增加了Rao-Blackwellized粒子滤波器粒子耗尽的几率。图4展示了RBPF算法在使用60个粒子时可以生成一致并且准确的地图，然而，此时产生的地图有时会产生双层墙壁。

 

 

4总结

本文介绍了一种由Doucet等提出的改进Rao-Blackwellized粒子滤波器构建栅格地图的算法。该方法基于最近的传感器信息，测距和扫描匹配过程的观测似然函数来计算高精度的后验概率密度函数。改进算法比原始算法应用了更少的粒子来构建地图，并且使用了一种更准确的方式分布采样粒子。此外，该算法使用了基于有效样本量的自适应重采样策略。该方法减少了粒子滤波器中不必要的重采样过程的次数，从而大大降低了粒子耗尽的风险。

 

 

该算法通过应用不同机器人装备激光测距仪进行了多次实验。在这些实验中，该算法所需的粒子数量通常比原始RBPF算法所需的粒子数小一个数量级，证明了其鲁棒性、优越性。

 

 

REFERENCES

http://blog.csdn.net/u010545732/article/details/17462941 粒子滤波(Particle filter)matlab实现
http://blog.csdn.net/heyijia0327/article/details/40899819  Particle Filter Tutorial 粒子滤波：从推导到应用
http://ishare.iask.sina.com.cn/f/24615049.html  粒子滤波理论