第六章 网络学习相关技巧2(权重设置)_设置权重

6.1简述

在神经网络的学习中，权重的初始值特别重要。设定什么样的权重初始值，经常关系到神经网络的学习能否成功。且会影响到神经网络学习的速度。

权值衰减：就是一种以减小权重参数的值为目的进行学习的方法。通过减小权重参数的值来抑制过拟合的发生。

因此，我们在对权值进行初始化的时候，一开始便可以将初始值设置较小，使用Gauss分布生成的值。但是权重的值也不能全部设置为0(或者权值全部相同)，将权重初始值设为0的话，将无法正确进行学习。这是因为在误差反向传播法中，所有的权重值都会进行相同的更新，没有意义。

6.2sigmiod权重初始值

下面使用sigmoid函数来举例，观察权重初始值是如何影响隐藏层的激活值的分布的。

目的：通过改变标准差，观察激活函数的变化

例：向一个5层神经网络（激活函数使用sigmoid函数）传入随机生成的输入数据，用直方图绘制各层激活值的数据分布。高斯分布的标准差分别为1， 0.01， 1/sqrt(n)。假设神经网络有5层，每层100个神经元。

1、当标准差为1时的直方图

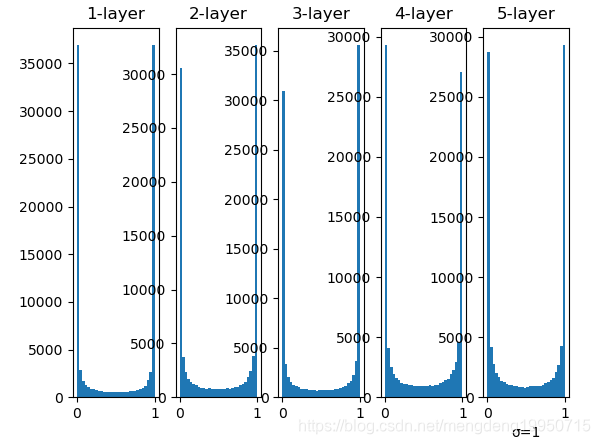
【注】随着输出不断地靠近0（或者靠近1），它的导数的值逐渐接近0。因此，偏向0和1的数据分布会造成反向传播中梯度的值不断变小，最后消失。这个问题称为梯度消失（gradient vanishing）。层次加深的深度学习中，梯度消失的问题可能会更加严重。

2、当标准差为0.01时的直方图

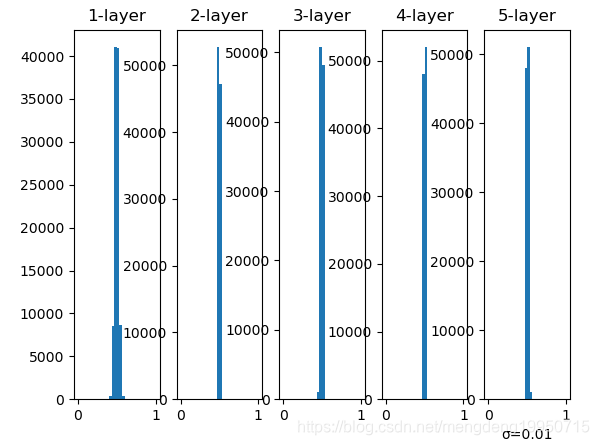
【注】这次呈集中在0.5附近的分布。因为不像刚才的例子那样偏向0和1，所以不会发生梯度消失的问题。但是，激活值的分布有所偏向，说明在表现力上会有很大问题。为什么这么说呢？因为如果有多个神经元都输出几乎相同的值，那它们就没有存在的意义了。比如，如果100个神经元都输出几乎相同的值，那么也可以由1个神经元来表达基本相同的事情。因此，激活值在分布上有所偏向会出现“表现力受限”的问题。

3、当标准差为1/sqrt(n)时的直方图(如果前一层的节点数为n，则初始值使用标准差为 1/sqrt(n)的分布)

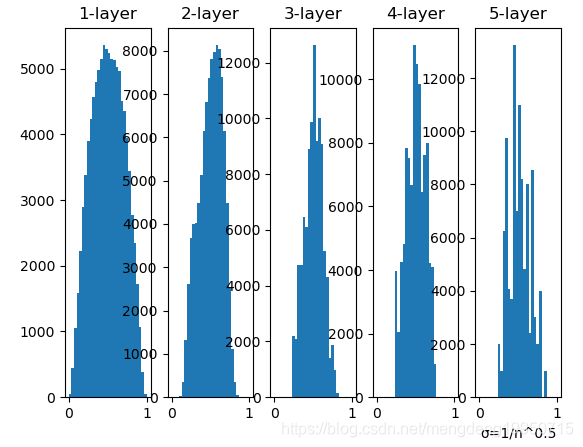
【注】从这个结果可知，越是后面的层，图像变得越歪斜，但是呈现了比之前更有广度的分布。因为各层间传递的数据有适当的广度，所以sigmoid函数的表现力不受限制，有望进行高效的学习。后面的层的分布呈稍微歪斜的形状。如果用 tanh函数（双曲线函数）代替 sigmoid 函数，这个稍微歪斜的问题就能得到改善。

代码实现如下：

import numpy as np
import matplotlib.pyplot as plt
 
 
def relu(x):
    return np.maximum(0, x)
 
 
def sigmoid(x):
    return 1/(1 + np.exp(-x))
 
 
def tanh(x):
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
 
 
x = np.random.randn(1000, 100)  # 1000个数据  # (1000, 100)
node_num = 100  # 各隐藏层的节点(神经元)数
hidden_layer_size = 5  # 隐藏层有5层
activations = {}  # 保存激活值的结果
 
for i in range(hidden_layer_size):  # 5
    if i != 0:
        x = activations[i - 1]
    # w = np.random.randn(node_num, node_num) * 1  # (100, 100)
    # w = np.random.randn(node_num, node_num) * 0.01
    w = np.random.randn(node_num, node_num)/np.sqrt(node_num)
    z = np.dot(x, w)  # (1000, 100)
    a = sigmoid(z)  # sigmoid函数
    activations[i] = a
# 绘制直方图
for i, a in activations.items():
    plt.subplot(1, len(activations), i+1)
    plt.title(str(i + 1)+"-layer")
    plt.hist(a.flatten(), 30, range=(0, 1))
 
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

6.3relu权重初始值

当激活函数使用ReLU时，一般推荐使用ReLU专用的初始值，也就是Kaiming He等人推荐的初始值，也称为“He初始值”。当前一层的节点数为n时，He初始值使用标准差为 的高斯分布。当Xavier初始值是 时，（直观上）可以解释为，因为ReLU的负值区域的值为0，为了使它更有广度，所以需要2倍的系数。

1、权重初始值为标准差是0.01的高斯分布

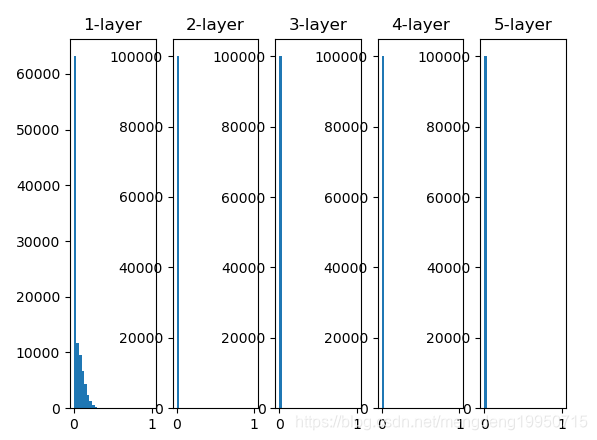
2、初始值为Xavier初始值时

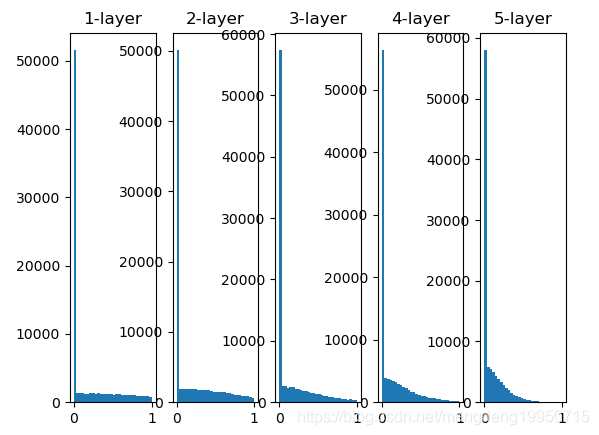
3、ReLU专用–“He初始值”

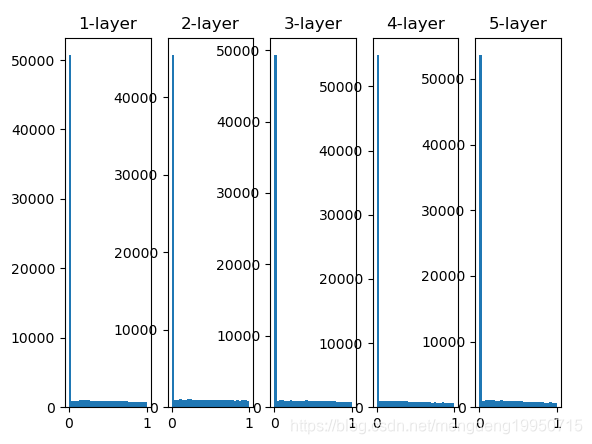
【注】1、当“std = 0.01”时，各层的激活值非常小。神经网络上传递的是非常小的值，说明逆向传播时权重的梯度也同样很小。2、初始值为Xavier初始值时的结果。在这种情况下，随着层的加深，偏向一点点变大。实际上，层加深后，激活值的偏向变大，学习时会出现梯度消失的问题。3、而当初始值为He初始值时，各层中分布的广度相同。由于即便层加深，数据的广度也能保持不变，因此逆向传播时，也会传递合适的值。

代码实现如下：

import numpy as np
import matplotlib.pyplot as plt
import math
 
 
def relu(x):
    return np.maximum(0, x)
 
 
def sigmoid(x):
    return 1/(1 + np.exp(-x))
 
 
def tanh(x):
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
 
 
x = np.random.randn(1000, 100)  # 1000个数据  # (1000, 100)
node_num = 100  # 各隐藏层的节点(神经元)数
hidden_layer_size = 5  # 隐藏层有5层
activations = {}  # 保存激活值的结果
 
for i in range(hidden_layer_size):  # 5
    if i != 0:
        x = activations[i - 1]
    # w = np.random.randn(node_num, node_num) * 1  # (100, 100)
    # w = np.random.randn(node_num, node_num) * 0.01  # 使用标准差为0.01
    # w = np.random.randn(node_num, node_num)/np.sqrt(node_num)  # 使用Xavier初始值作为权重初始值
    w = math.sqrt(2) * np.random.randn(node_num, node_num)/ np.sqrt(node_num)
    z = np.dot(x, w)  # (1000, 100)
    # if i <= 1:
    #     a = sigmoid(z)  # sigmoid函数
    # else:
    #    a = tanh(z)
    a = relu(z)
    activations[i] = a
 
for i, a in activations.items():
    plt.subplot(1, len(activations), i+1)
    plt.title(str(i + 1)+"-layer")
    # flatten是numpy.ndarray.flatten的一个函数，即返回一个一维数组。默认按行的方向降维
    # 参数range的类型为tuple型，指定全局间隔(min,max),分为30个条状图
    plt.hist(a.flatten(), 30, range=(0, 1))
 
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

6.4案例：不同初始值比较

基于std = 0.01、Xavier初始值、He初始值等不同的权值对MNIST手写数字进行比较

目录结构：

6.4.1common文件夹

（funtions.py, gradient.py, layers.py, multi_layer_net.py, optimizer.py, util.py）见前面博文

6.4.2ch06文件夹

6.4.2.1weight_init_compare.py

# coding: utf-8
import os
import sys
 
sys.path.append(os.pardir)
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import SGD
 
 
# 0:读取数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
 
train_size = x_train.shape[0]
batch_size = 128
 
max_iterations = 2000
 
 
# 1:设置权重初始值的方式
weight_init_types = {'std=0.01': 0.01, 'Xavier': 'sigmoid', 'He': 'relu'}
optimizer = SGD(lr=0.01)
 
networks = {}
train_loss = {}
# 初始化网络
for key, weight_type in weight_init_types.items():
    networks[key] = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100],
                                  output_size=10, weight_init_std=weight_type)
    train_loss[key] = []
 
 
# 2:训练2000次
for i in range(max_iterations):
    # 批处理
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
 
    # 梯度更新
    for key in weight_init_types.keys():
        grads = networks[key].gradient(x_batch, t_batch)
        optimizer.update(networks[key].params, grads)
    
        loss = networks[key].loss(x_batch, t_batch)
        train_loss[key].append(loss)
    
    if i % 100 == 0:  # 20次
        print("===========" + "iteration:" + str(i) + "===========")
        for key in weight_init_types.keys():
            loss = networks[key].loss(x_batch, t_batch)
            print(key + ": " + str(loss))
 
 
# 3.绘图
markers = {'std=0.01': 'o', 'Xavier': 's', 'He': 'D'}
x = np.arange(max_iterations)
for key in weight_init_types.keys():
    plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 2.5)
plt.legend()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

6.4.3结果

这个实验中，神经网络有5层，每层有100个神经元，激活函数使用的是ReLU。

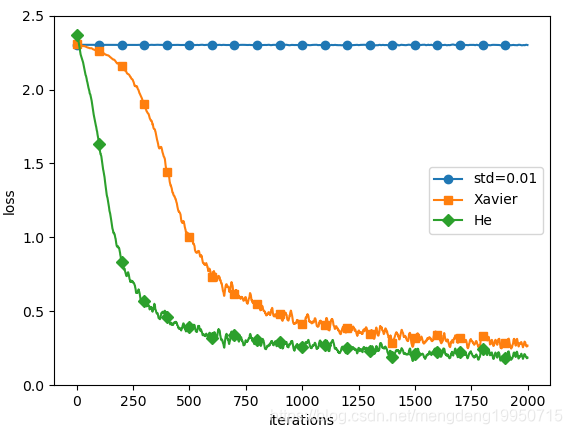
【注】从上图的结果可知，当std = 0.01时完全无法进行学习。这和刚才观察到的激活值的分布一样，是因为正向传播中传递的值很小（集中在0附近的数据）。因此，逆向传播时求到的梯度也很小，权重几乎不进行更新。相反，当权重初始值为Xavier初始值和He初始值时，学习进行得很顺利。并且，我们发现He初始值时的学习进度更快一些。