经典算法-----农夫过河问题（深度优先搜索）

目录

前言

农夫过河问题

1.问题描述

2.解决思路

位置编码

获取位置

判断是否安全 

 深度优先遍历（核心算法）

 3.完整代码

---

前言

        今天我们来解决一个有意思的问题，也就是农夫过河问题，可能这个问题我们小时候上学就听说过类似的问题，当时我们的解决方法就是一个一个列举，反复去找，但是在编程上对于这个问题的解决方法就是去通过回溯问题来找出全部的可能来解决这个问题，下面就一起来看看吧。

农夫过河问题

1.问题描述

一位农夫、一只狼、一只羊和一颗白菜都在河的一侧，他们想到河的另一侧。河中有一条船，一次只能载农夫和一个物体（狼或羊或白菜）。若农夫不在的时候，狼会吃掉羊，羊会吃掉白菜。问：该以什么样的方式才能将狼、羊和白菜完好的运到对岸？

在此之前我们先去通过自己思考一下怎么去过河，很简单：① 农夫把羊运到河岸1；② 农夫回来河岸0；③ 把白菜运往河岸1；④ 把羊运到河岸0；⑤ 把狼运到河岸1；⑥ 再回来河岸0；⑦ 把羊运往河岸1，最后完成过河。当然方法不止这一种，如果让你去写编程的话找出全部的方法，怎么写呢？

2.解决思路

位置编码

不妨设，当前其实岸为南岸即标记为0，目标岸北岸标记为1，然后分别通过一个二进制数来表示农夫、狼、羊、白菜的当前位置，比如1000（十进制为8）表示农夫当前位置在北岸，其他三个在南岸，以此类推0100（十进制为4）表示狼在北岸，0010（十进制为2）表示羊在北岸，0001（十进制为1）表示白菜在北岸，通过以上的规则我们可以明确的表示这4者的位置关系。

获取位置

        前面既然有了编码来表示位置关系，那么我假设当前4者的关系位置为 location，那如何获取到当前农夫、狼、羊、白菜的位置呢？

        很简单，只需要进行与运算就行了，比如location=1010，即表示农夫在北岸，狼在南岸，羊在北岸、白菜在南岸，那么我要知道农夫的位置只需要进行 location&8 的运算即可，得出的二进制数结果就是1000（十进制为8），即农夫在北岸.

//判断当前位置
int farmer(int loca) {//loca是表示当前4者的位置状态二进制数
	return ((loca & 8) == 8);
}
int wolf(int loca) {
	return ((loca & 4) ==4);
}
int sheep(int loca) {
	return ((loca & 2) ==2) ;
}
int cabbage(int loca) {
	return  ((loca & 1)==1);
}

判断是否安全 

既然有了位置，那就要去判断这种情况是否安全了，农夫不在狼和羊不可以在一起，农夫不在白菜和羊不可以在一起，

int isSafe(int loca) {
	int a, b, c, d;
	a = farmer(loca);
	b = wolf(loca);
	c = sheep(loca);
	d = cabbage(loca);
	if (a != c && c == d)//农夫不在白菜和羊不可以在一起，不安全
		return 0;
	else if (a != b && b == c)//农夫不在狼和羊不可以在一起，不安全
		return 0;
	else
		return 1;
}

 深度优先遍历（核心算法）

        要想找到全部的运输方法那就需要去进行深度遍历，由于总共有16个状态，所以在此之前需要一个数组来储存表示当前的位置状态route[16]，全部初始化为-1表示没有没有访问过这个运算过程，其中第一个状态也就是0000，最开始的时候4者都在南岸，那么route[0]=-2，表示最开始状态不需要去访问或者修改操作。

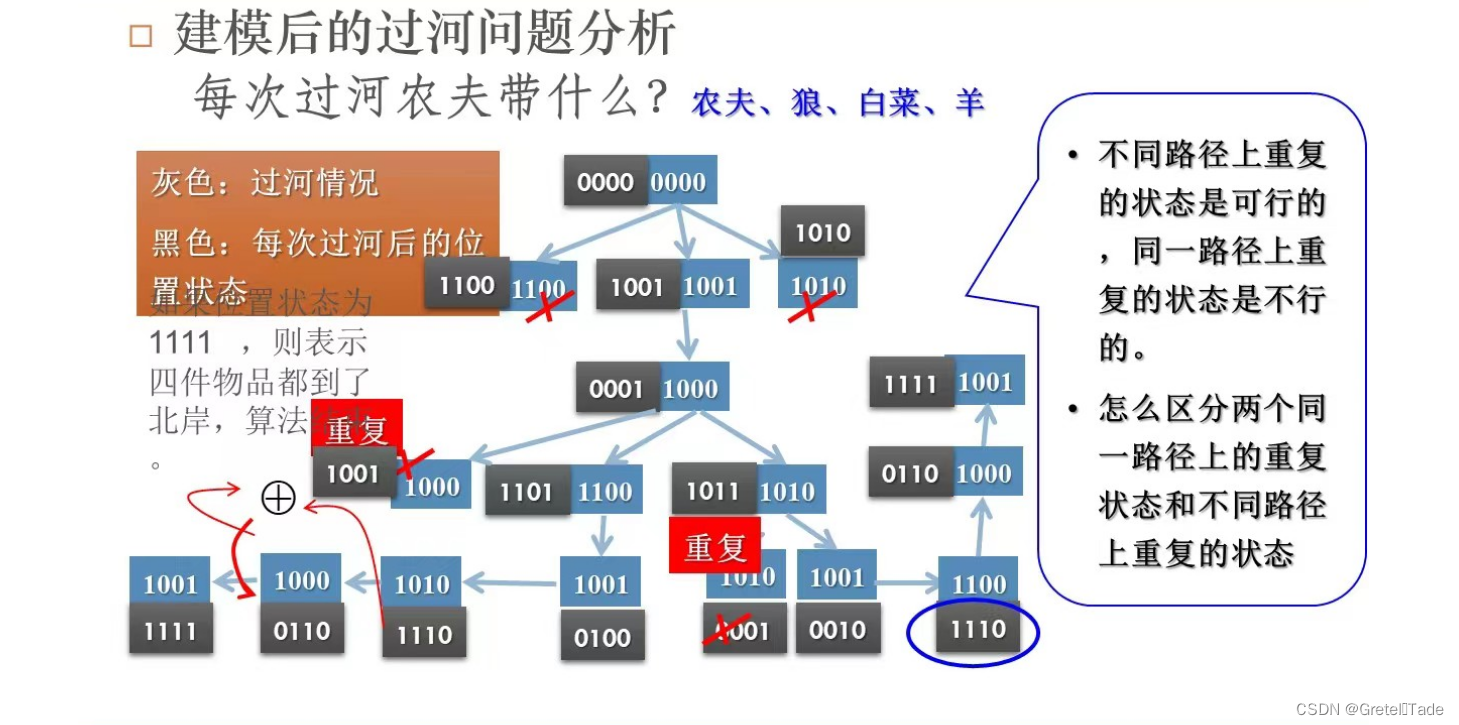
每次带一个物品过河，我们可以通过循环来实现二进制数的左移，从白菜开始向左移动，直到农夫，movers表示当前要进行移动的物体，这时候我们就需要算出如果这个物品移动之后，下一个状态nextlocation是否安全，如果满足条件的话，那就吧进行这一步移动操作，如果不安全那就换一个物体去移动，如果直到移动到农夫也不安全，那就进行回溯到上一步，从上一步重新开始移动下一个物体，以此类推，这就是一个深度遍历回溯的过程。

 

//深度遍历核心算法（回溯算法）
void process(int loca,int* route,int* count) {
	if (route[15] == -1) {
		//move表示要移动当前物体
		for (int move = 1; move <= 8; move <<=1) {
			//如果农夫与当前要移动的物体处于同一个岸的话
			if (((loca & 8)!=0) == ((loca & move)!=0)) {				
				int next_loca = loca ^ (8 | move);//获取下一个状态next_loca二进制数
				if (isSafe(next_loca) && route[next_loca] == -1) {//判断下一个状态是否安全,同时也没有访问过
					int next_route[16];
					for (int i = 0; i < 16; i++) {//把当前的路径复制一份，进入到下一步递归,以保证这一步的路径数据没被修改，进行回溯操作
						next_route[i] = route[i];
					}
					next_route[next_loca] = loca;//存储当前位置，进入到下一个
					process(next_loca, next_route,count);//回溯
				}
			}
		}
	}
	//如果route[15]储存了数据，那么都到达了对岸了，打印结果
	else {
		print(route, 15,count);
		puts("\n");
	}
	return;
}

 3.完整代码

#include<stdio.h>
#include<string.h>
 
//北1  南0
//判断当前位置
int farmer(int loca) {
	return ((loca & 8) == 8);
}
int wolf(int loca) {
	return ((loca & 4) ==4);
}
int sheep(int loca) {
	return ((loca & 2) ==2) ;
}
int cabbage(int loca) {
	return  ((loca & 1)==1);
}
 
int isSafe(int loca) {
	int a, b, c, d;
	a = farmer(loca);
	b = wolf(loca);
	c = sheep(loca);
	d = cabbage(loca);
	if (a != c && c == d)//农夫不在白菜和羊不可以在一起，不安全
		return 0;
	else if (a != b && b == c)//农夫不在狼和羊不可以在一起，不安全
		return 0;
	else
		return 1;
}
//打印结果
void print(int* route,int status,int* count) {
	if (status == -2) {
		*count += 1;
		printf("第%d种方法：\n",*count);
		printf("start");
		return;
	}
	print(route, route[status],count);
	printf("->%d", status);
}
 
//深度遍历核心算法（回溯算法）
void process(int loca,int* route,int* count) {
	if (route[15] == -1) {
		//move表示要移动当前物体
		for (int move = 1; move <= 8; move <<=1) {
			//如果农夫与当前要移动的物体处于同一个岸的话
			if (((loca & 8)!=0) == ((loca & move)!=0)) {				
				int next_loca = loca ^ (8 | move);//获取下一个状态next_loca二进制数
				if (isSafe(next_loca) && route[next_loca] == -1) {//判断下一个状态是否安全,同时也没有访问过
					int next_route[16];
					for (int i = 0; i < 16; i++) {//把当前的路径复制一份，进入到下一步递归,以保证这一步的路径数据没被修改，进行回溯操作
						next_route[i] = route[i];
					}
					next_route[next_loca] = loca;//存储当前位置，进入到下一个
					process(next_loca, next_route,count);//回溯
				}
			}
		}
	}
	//如果route[15]储存了数据，那么都到达了对岸了，打印结果
	else {
		print(route, 15,count);
		puts("\n");
	}
	return;
}
 
int main() {
 
	int route[16];
	memset(route, -1, sizeof(route));
	route[0] = -2;
	int count = 0;//统计
	process(0,route,&count);
}

输出结果：

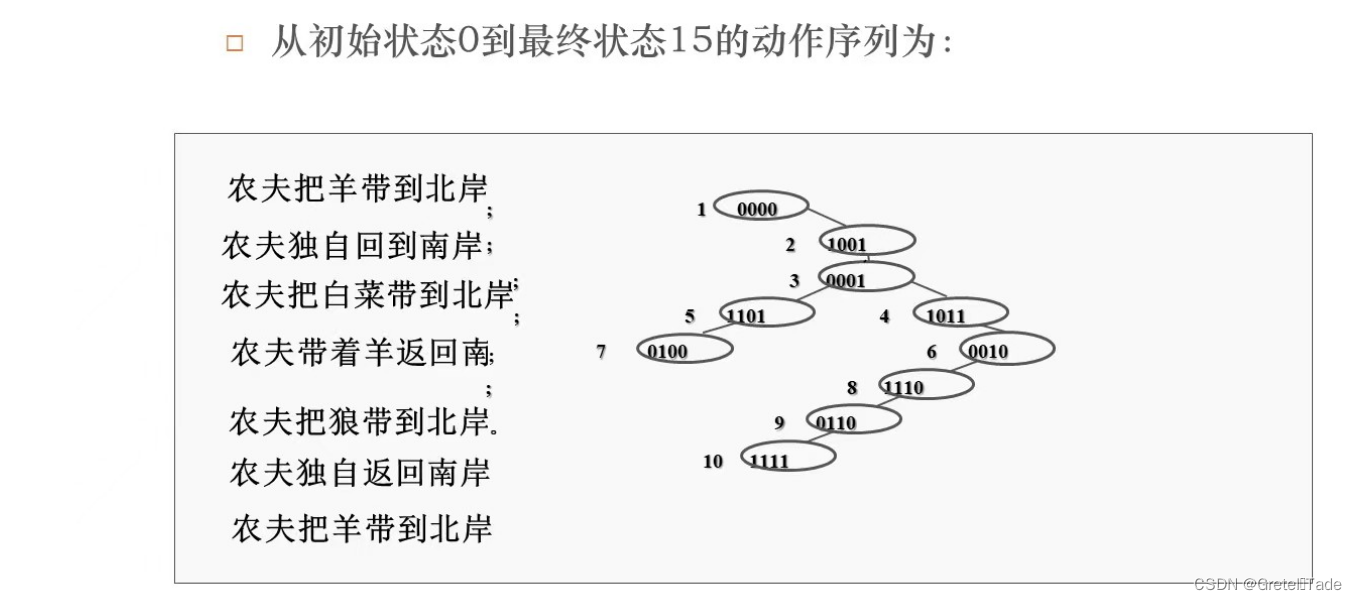 以上就是今天的全部内容了，你们学会这个问题的解决方法吗？是不是很有意思呢？

分享一张壁纸：