热门标签
热门文章
- 1关于windows安全权限_d盘user默认权限
- 2android交叉编译C++代码_android-ndk-r23 sysroot目录在哪
- 3c语言字符串复制两种方法,字符串复制的几种方法
- 4怎样优雅地增删查改(三):业务用户的增数据结构就下面几个删查改
- 5打包部署若依SpringBoot后端和Vue前端_若依前端打包命令
- 6Android Studio运行项目闪退_android studio的虚拟机一运行项目就闪退
- 7微信小程序、uniapp自定义底部导航栏(附源码)_uniapp 使用 自定义底部导航
- 8STM32CubeMX实战教程(四)——基本定时器(还是点灯)
- 9关联规则之序列模式挖掘--GSP算法
- 10HTML~_报错
当前位置: article > 正文
MATLAB实现皮尔逊相关系数热力图绘制_相关系数图matlab
作者:weixin_40725706 | 2024-04-28 15:57:22
赞
踩
相关系数图matlab
皮尔逊相关系数是用来衡量两个连续变量之间线性相关性的统计度量。它测量变量之间的线性程度,其值范围从-1到1。绘制热力图属于数据可视化的一部分,可以帮助我们更直观地了解特征之间的相关性。其计算公式为:
其中r为Pearson相关系数,X和Y为变量,µY为变量X的平均值,µY为变量Y的平均值,r的绝对值越大,说明两个特征之间的相关性越高。r的具体含义如表1所r
| r | 相关强度 |
| [−1, −0.6] | 强负相关 |
| (−0.6, −0.4] | 中等负相关 |
| (−0.4, −0.2] | 弱负相关 |
| (−0.2, 0.2) | 极弱负相关/不相关 |
| [0.2, 0.4) | 弱正相关 |
| [0.4, 0.6) | 中等正相关 |
| [0.6, 1] | 强正相关 |
本文所使用的数据集形式如下:
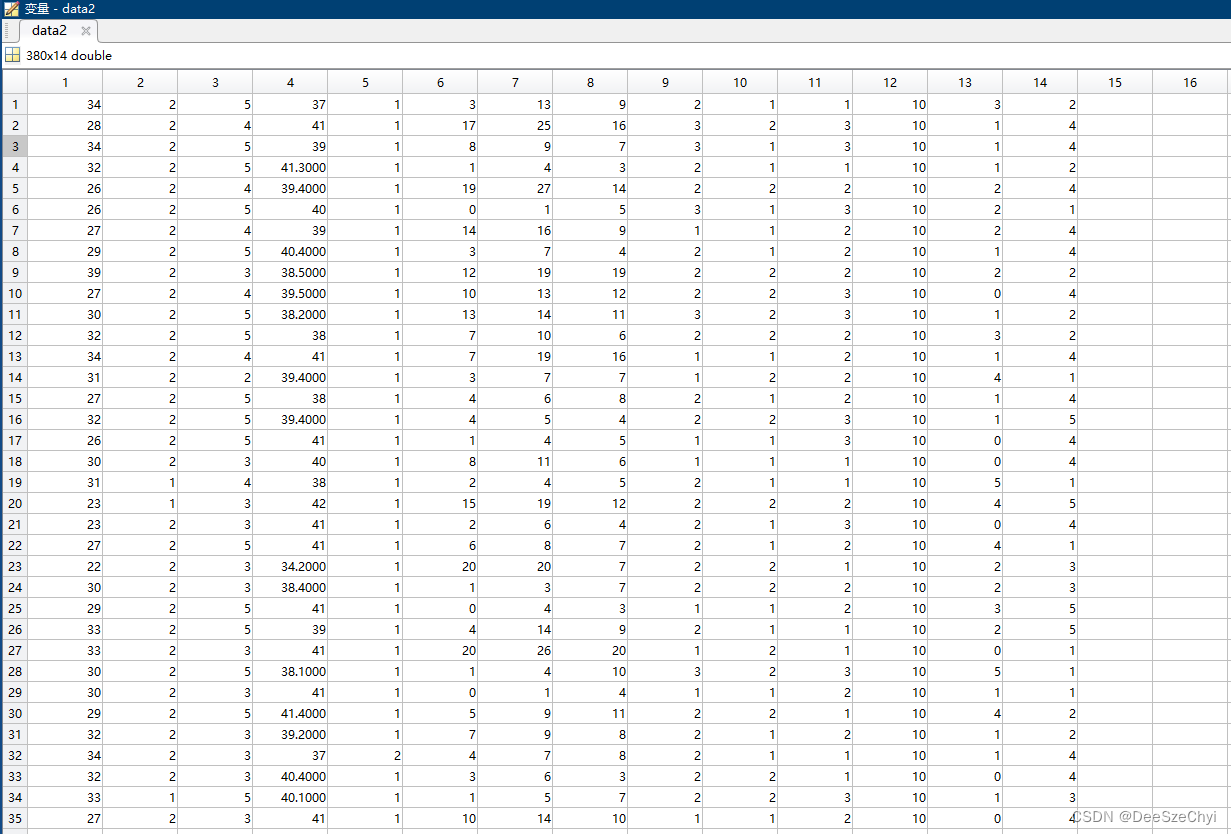
该数据每列代表一个特征维度,本文所要绘制的皮尔逊相关系数热力图为14x14。matlab代码:
- figure
- rho = corr(data2, 'type','Pearson');
- string_name={'年龄','婚姻','教育','妊娠','分娩','CBTS','EPDS','HADS','行为特征','性别','年龄','睡眠质量','次数','入睡方式'};
- xvalues = string_name;
- yvalues= string_name;
- h = heatmap(rho);
- h.Title = '相关系数';
- colormap summer
rho = corr(data2, 'type','Pearson');该处可以将'Pearson'替换成'Kendall' 或 'Spearman'。本文使用的是Pearson相关系数。
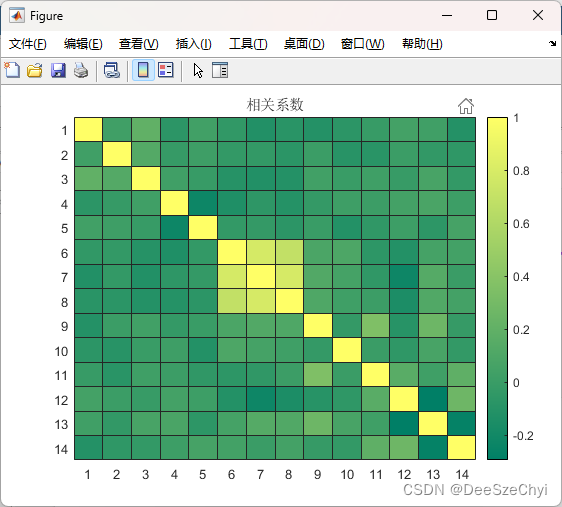
从绘制的热力图可以看出,第6,7,8特征之间具有较强的相关性。
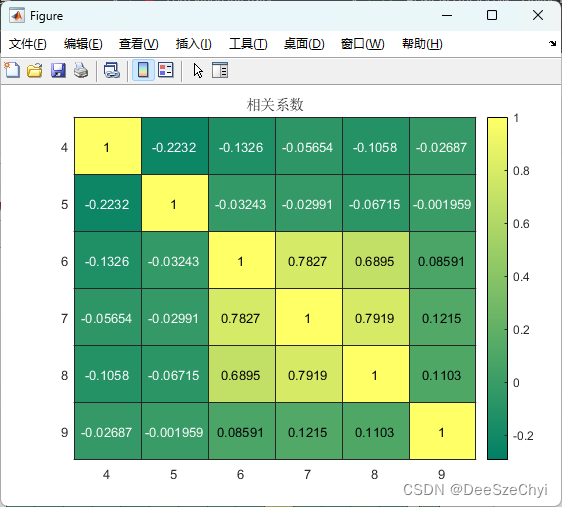
我们将图片放大可以看到它们的皮尔逊相关系数,对照上文的表格可以看出它们是强正相关。
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/weixin_40725706/article/detail/503092
推荐阅读
相关标签


