异常值检测大揭秘：多种方法应对数据异常(附代码)_数据异常值查找方法的代码

1、背景介绍

当我们在进行数据分析的时候，数据中常常会存在一些异常值。这些异常值可能是由于人为录入错误、仪器故障或者其他原因导致的，但它们对于最终的数据分析结果却有极大的影响。如果不及时发现并处理这些异常值，就会导致误判和误导，进而影响决策和结果准确度。

因此，异常值检测与处理是数据分析过程中不可或缺的环节。通过有效的异常值检测与处理方法，我们可以排除干扰因素，提高数据的准确性和可靠性，从而更加精准地进行数据分析和科学研究。

本文将介绍异常值的概念及其影响、异常值检测与处理的重要性，以及针对异常值检测与处理的实验原理和实现。希望通过本文的介绍，读者能够更好地了解异常值检测与处理的意义，掌握相关方法的使用和操作，提高数据分析的准确性和可靠性。

本期内容『数据+代码』已上传百度网盘。有需要的朋友可以关注公众号【小Z的科研日常】，后台回复关键词[异常值]获取。

2、实验原理和方法

在数据分析过程中，异常值检测与处理是非常重要的环节。为了帮助读者更好地了解异常值检测与处理的方法和原理，本文将介绍常用的离群点检测方法，包括：

1.IQR方法：根据数据的四分位数范围来判断数据是否为异常值。

2.Z-Score方法：通过计算数据的标准差和均值，判断数据是否偏离正常范围。

3.Isolation Forest方法：基于随机森林的思想，将数据划分为不同的子空间，从而识别出异常值。

4.局部离群因子法：通过计算每个数据点周围的局部密度，来判断数据是否为异常值。

5.SVM方法：将数据集视为一个类别，训练模型后通过预测结果来筛选出异常值。

6.DBSCAN方法：通过聚类的方式将数据分类，进而识别出异常值。

以上方法各具特点，可以根据实际需要选择合适的方法来进行异常值检测与处理。下面我将对以上方法原理进行讲解。

2.1 IQR方法

IQR方法是一种基于数据分布的离群点检测方法，其主要思想是通过计算数据的四分位距（IQR）来确定异常值的阈值。具体步骤如下：

1.计算数据的第一四分位数（Q1）、第二四分位数（中位数）和第三四分位数（Q3）。

2.计算IQR = Q3 - Q1。

3.确定一个常数k（通常取1.5或3），并计算下限lower = Q1 - k * IQR和上限upper = Q3 + k * IQR。

4.如果某个数据点小于lower或大于upper，则将其视为异常值。

IQR原理图:

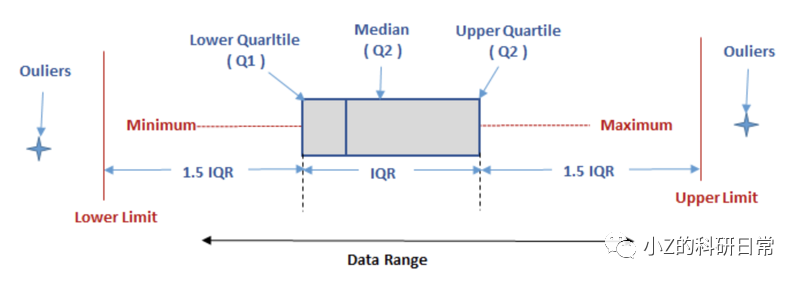
IQR方法比较简单并且易于理解，常用于数据分布相对稳定的场景中。但是，它也有一些缺点，例如无法处理非连续型的异常值（例如离群点集中在两个分布之间），以及对于数据分布不均匀的情况可能产生误判。

Q1 = features.quantile(0.25)
Q3 = features.quantile(0.75)
IQR = Q3 - Q1
features = features[~((features < (Q1 - 1.5 * IQR)) |(features > (Q3 + 1.5 * IQR))).any(axis=1)]

2.2 Z-Score方法

Z-Score方法是另一种常用的异常值检测方法。在这种方法中，我们计算数据的均值和标准差，然后将每个数据点转换为其Z-Score值。Z-Score值表示该数据点与整个数据集均值的偏差程度，具体步骤如下：

1.计算数据的平均值和标准差。

2.对每个数据点，计算其与平均值之间的偏离程度，即Z-Score = (x - mean) / std。

3.根据设定的阈值，判断每个数据点的Z-score值是否超过该阈值。如果超过，则该数据点被认为是异常值。

其中，x表示数据点的值，mean表示数据集的均值，std表示数据集的标准差。如果某个数据点的Z-Score值超过预设的阈值，就可以将其视为异常值。

代码如下：

#使用Z-Score方法去除异常值
z_scores = np.abs(stats.zscore(features))
features = features[(z_scores < 3).all(axis=1)]

在异常值检测时，一般认为偏离3倍标准差以上为异常值:

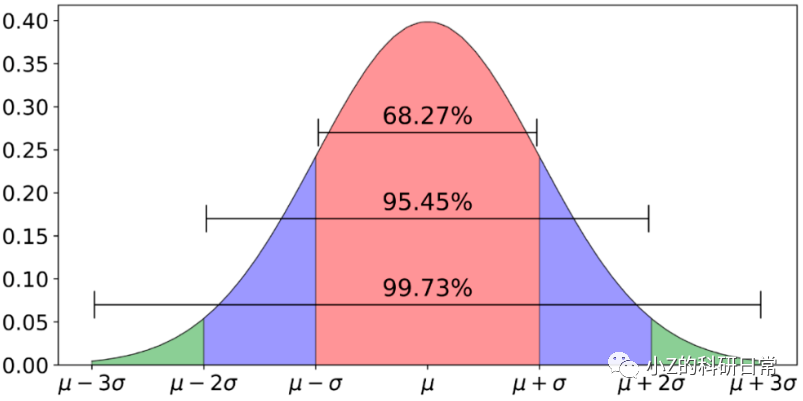
2.3 Isolation Forest方法

Isolation Forest是一种基于树结构的异常检测算法。它通过随机选择一个特征和该特征的一个分割点，将样本空间划分为左右两个子区域，然后对每个子区域进行递归划分，直到每个子区域只包含一个样本点或达到预设的最大深度。最终形成一个以根节点为起点，叶子节点为终点的树型结构，如下图所示：

接着，我们需要计算每个样本点在这棵树上的路径长度，即从根节点到该样本点经过的边数。路径长度越短，表示该样本点与其他样本点之间的差异越大，可能是一个异常值；反之，则是正常样本。

最后，我们需要设置一个阈值来判断哪些样本点是异常值。通常采用的方法是，计算所有样本点的路径长度的平均值，如果某个样本点的路径长度小于平均值，则被认为是异常值。具体过程如下：

1.从数据集中随机选择一个特征f和一个范围在该特征取值范围内的分割点v；

2.将数据集划分成左右两个子集，其中左子集包含所有特征f小于v的样本，右子集包含所有特征f大于等于v的样本；

3.如果左子集或右子集为空，则终止构建孤立树；否则，递归地对左右子集继续执行步骤a)和b)，直到达到预定的树深度或无法再继续划分。

假设有m个样本，每个样本有n个特征。对于第t棵孤立树，令样本集合为Xt，构建深度为ht的二叉树Tt。我们用ct(x)表示样本x在Tt中的路径长度，即从根节点到x所经过的边数减去1。根据算法流程，ct (x)的计算过程可以表示如下：

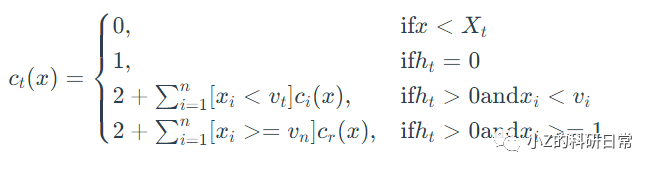
其中vti表示第t棵孤立树中随机选择的特征ft的一个分割点。l和r分别表示x在左子树和右子树中所处的位置。

isolation_forest = IsolationForest(n_estimators=100, contamination=0.1, random_state=42)
isolation_forest.fit(features)
y_noano = isolation_forest.predict(features)

2.4 局部离群因子法

LOF法通过计算每个数据点与其邻居之间的密度比值来确定其是否为异常值。具体地，对于一个数据点，如果其周围的邻居密度相对较小，则认为该数据点是一个异常值。要使用LOF法来检测异常值，具体步骤如下：

1. 选择一个合适的数据集，并确定每个数据点的特征向量。

2. 对于每个数据点，计算其k近邻（k-Nearest Neighbors，kNN）集合:

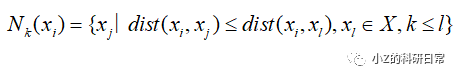
其中k是一个用户定义的参数，通常是一个较小的整数。

3. 计算每个数据点与其k近邻之间的可达距离（Reachability Distance，RD）。可达距离表示从当前数据点到其k近邻中最远点的距离。

可达距离越大，说明当前数据点与其k近邻之间的密度越小。定义第i个数据点xi到j的可达距离（Reachability Distance）为：

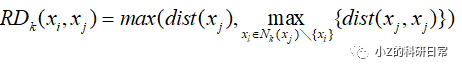
其中Nk(xj)\{xi}表示xj的k近邻集合中排除了xi，即不考虑xi本身的影响。

4.定义第i个数据点的局部离群因子为:

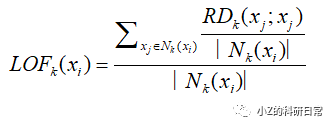
其中Nk(xi)表示xi的k近邻数量。计算每个数据点的局部离群因子（LOF）。LOF表示当前数据点相对于其k近邻之间的密度比值。LOF值越大，说明当前数据点相对于其邻居之间的密度越小，越有可能是一个异常值。通常，我们将LOF值大于某一阈值的数据点标记为异常值。

local_outlier_factor = LocalOutlierFactor(n_neighbors=20, contamination=0.1)
y_noano = local_outlier_factor.fit_predict(features)

2.5 SVM算法

SVM法是一种基于数据点与边界之间的距离进行异常值检测，假设我们有一个训练集

X={x1,x2,...,xm}，其中每个数据点都被标记为正常（y=0）或异常（y=1）。我们的目标是找到一个决策边界（decision boundary），将正常数据和异常数据分开。SVM算法通过寻找一个最大间隔超平面（maximum margin hyperplane）来构建这个边界。超平面是一个分割数据空间的线性函数，它将数据分成两个部分。如图:

实现步骤如下：

1.定义超平面：我们先定义一个超平面 wx+b=0，其中w是法向量（normal vector），b 是偏置项（bias term）。

2.确定分类规则：对于任意数据点 xi，如果w.xi+b⩾0，则将其归为正常数据；否则，将其归为异常数据。

3. 最大化间隔：在确定分类规则后，我们需要找到一个最大间隔超平面，使得正常数据与异常数据之间的距离最大化。距离可以使用欧几里得距离计算。

具体地，对于每个数据点xi，我们可以计算其到超平面的距离为：

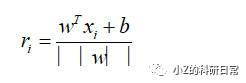
由于我们希望距离最大化，因此需要找到一个超平面，使得所有距离 ri的最小值最大化。这可以表示为以下优化问题：

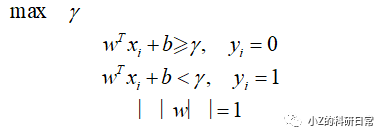
其中，γ 表示距离的最小值。

4. 转化为对偶问题：我们将优化问题转化为对偶问题，通过求解对偶问题可以更方便地得到最优解。具体地，对偶问题为:

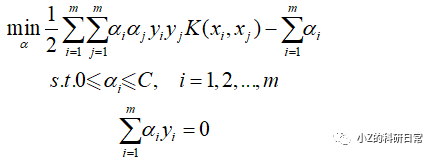
其中，C 是一个正则化常数，K(xi,xj) 是核函数（kernel function）。通过求解上述优化问题，可以得到最优的 α值。

5. 计算法向量和偏置项

通过最优的 α 值可以计算出法向量 w 和偏置项 b：

6. 检测和处理异常点：训练完成后，就可以使用它来检测和处理异常点了。具体步骤如下：

a）将新的数据点x 输入到模型中，计算其到超平面的距离：
 

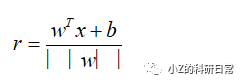
b）如果r超过某个阈值，则将该数据点标记为异常点；否则，将其标记为正常数据。

one_class_svm = OneClassSVM(nu=0.1, kernel='rbf', gamma=0.1)
y_noano = one_class_svm.fit_predict(features)

2.6 DBSCAN算法

DBSCAN通过计算数据点之间的密度来确定簇的边界，并将不属于任何簇的数据点视为异常。

其原理是寻找高密度区域，并将这些区域划分为一个簇。具体而言，对于每个数据点，算法会计算其半径ε内的邻域中的点数，如果点数超过了阈值MinPts，则该点被认为是核心点。然后，算法会以核心点为起点，沿着密度可达路径来扩展簇，直到无法再添加新的点为止。

如果某个数据点不是核心点，但在某个核心点的邻域内，那么它就被归为该核心点所在的簇。否则，该数据点就被视为噪声或异常值。具体步骤如下：

1.随机选择一个未访问的数据点p。

2.如果p的邻域内点的数量小于MinPts，标记p为噪声点。

3.否则，创建一个新的簇C，并将p加入C。

4.对于p邻域内的每个数据点q： a. 如果q未被访问，将其标记为已访问并加入C b. 如果q是核心点，则递归地处理其邻域内的数据点。

5.重复步骤1-4，直到所有点都被访问过。

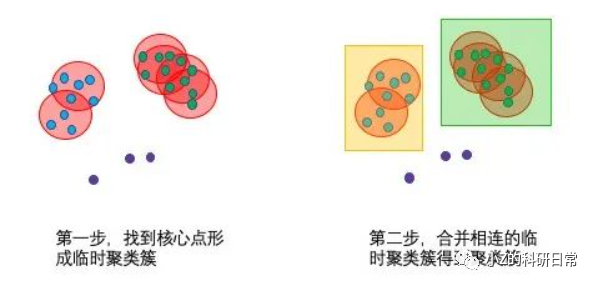
现在我们来推导DBSCAN算法的核心公式。假设有一个数据集D={x1,x2,...,xn}，其中每个数据点xi都有一个密度ρi。我们定义半径ε内的密度为：

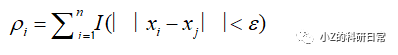
其中，I(·)是指示函数，如果括号内的条件成立则输出1，否则输出0。也就是说，ρi是距离xi不超过ε的点的数量。

接下来，我们定义一个数据点xi的可达距离δ(p,q)，表示从p出发，沿着密度可达路径到达q的最短距离。具体而言，对于任意两个数据点p和q，它们的可达距离为：

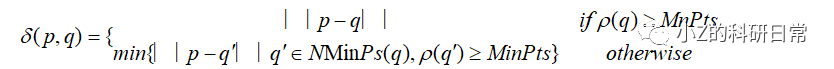
其中，NMinPts(q)表示以q为中心、半径为ε的邻域内包含的核心点的集合。

最后，我们定义一个数据点xi的局部离群因子LOF(xi)，表示其密度相对于周围点的密度的比值：

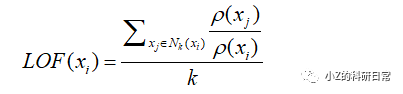
DBSCAN算法的性能较为敏感，需要调节好参数才能得到较好的聚类结果。具体而言，需要设置合适的半径ε和邻域内最小点数MinPts。如果ε太小，则会将噪声点误认为是簇的一部分；如果ε太大，则会将不同的簇合并在一起。同样地，如果MinPts太小，则会产生过多的簇；如果MinPts太大，则会导致很多数据点被视为噪声。

dbscan = DBSCAN(eps=0.5, min_samples=10)
y_noano = dbscan.fit_predict(features)

3、实验结果展示

本次实验使用波士顿房价数据集，通过Python实现不同方法进行异常值检测的效果。首先通过对原始数据绘制小提琴图进行分析：

通过小提琴图，可明显观察出，Dis、Ptratio特征具有较多异常值。下面将对不同方法去除离群点后的数据分布情况进行可视化展示，并对比不同方法去除离群点前后的特征值分布情况。

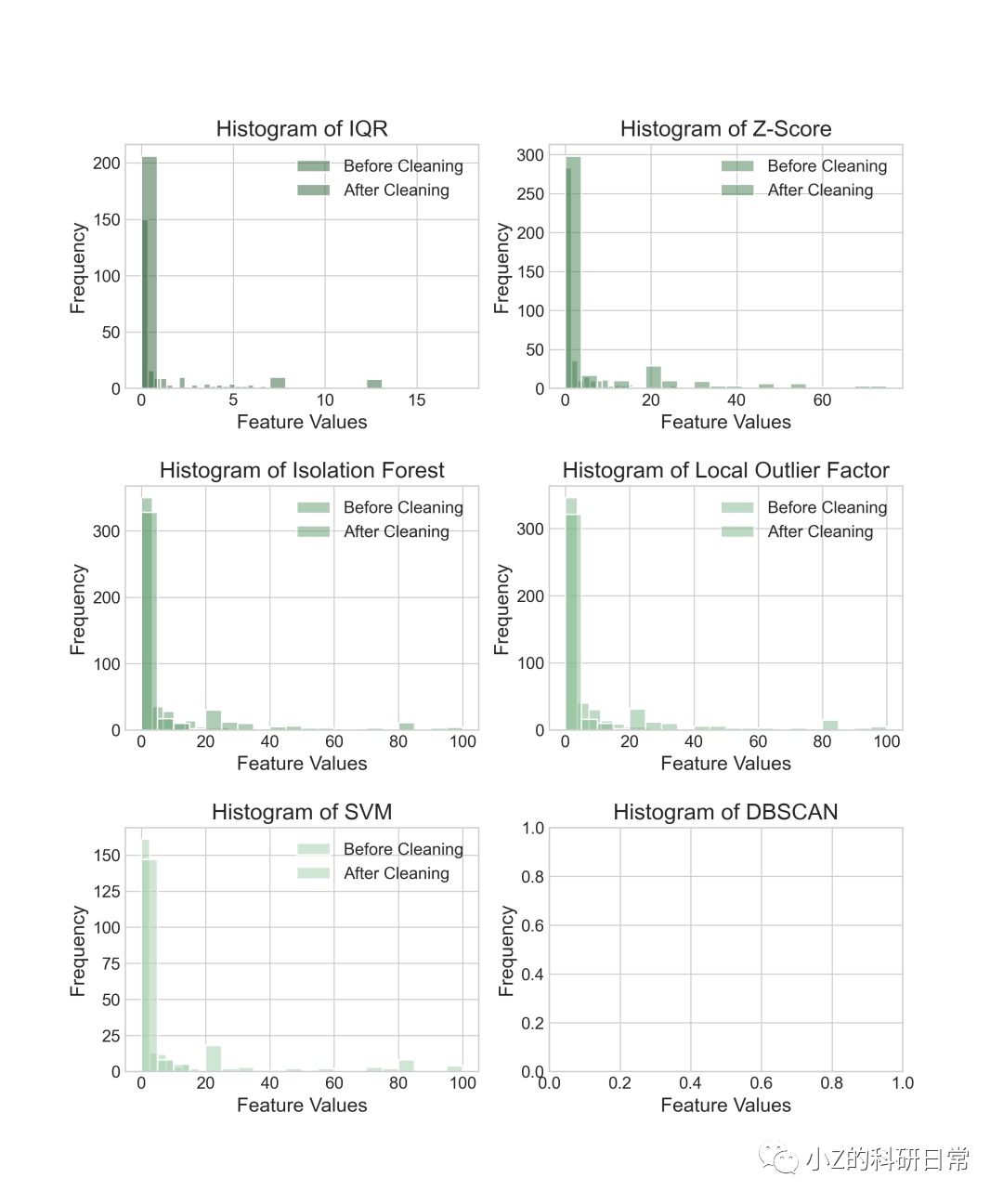
从上述两个图可以看出，无论那种方法，特征均集中0-5区域内。在使用IQR方法、Z-Score方法和Isolation Forest方法去除离群点后，5-80内均出现一些离散点使各特征均值化；而在使用局部离群因子法、单类SVM方法和DBSCAN方法去除离群点后，数据分布变得更加集中，但仍然存在一些离群点。此外，还可以看到，在使用IQR方法去除离群点前后，数据的标准差和极差明显减小，说明该方法能有效地降低数据的异常程度。

接着，我们可以进一步使用箱线图来观察不同方法去除离群点后的数据分布情况。如下所示：

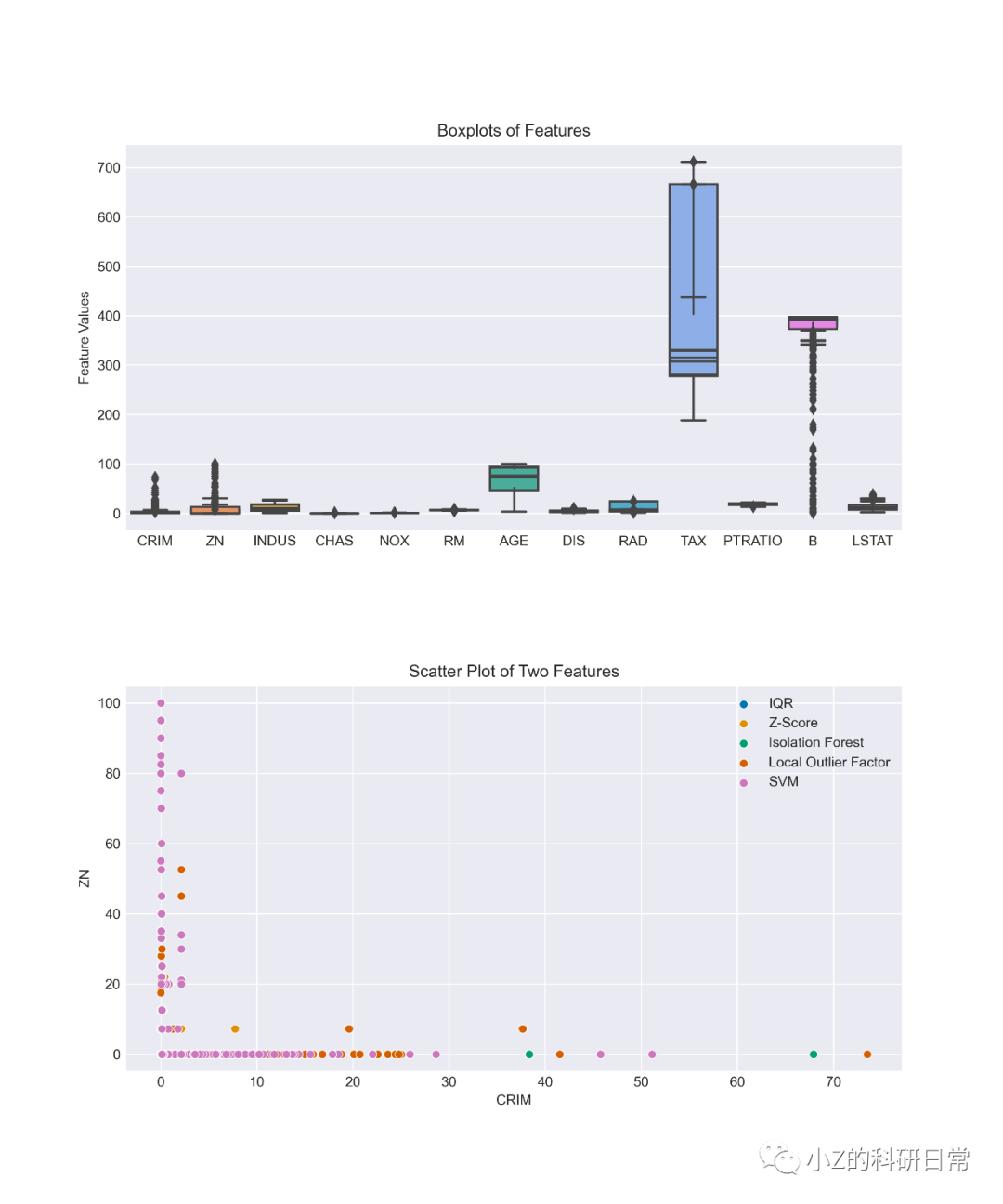
从上图可以看出，在使用局部离群因子法、单类SVM方法和DBSCAN方法去除离群点后，数据分布变得更加紧密，但仍然存在一些远离主体的离群点。而在使用IQR方法、Z-Score方法和Isolation Forest方法去除离群点后，数据分布较为均匀，且离群点明显减少。

最终的结果表明，不同的方法可能会产生不同的结果，因此在实际应用中需要选择最适合自己数据集的方法。同时，在进行异常值检测和清理时，也需要根据具体情况进行选择和调整。

感谢您阅读本篇文章！如果您对数据分析和异常值检测方法感兴趣，欢迎关注我们的微信公众号（小Z的科研日常）。