leetCode 188.买卖股票的最佳时机 IV 动态规划 + 状态压缩

给你一个整数数组 prices 和一个整数 k ，其中 prices[i] 是某支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说，你最多可以买 k 次，卖 k 次。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1：

输入：k = 2, prices = [2,4,1]
输出：2
解释：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

示例 2：

输入：k = 2, prices = [3,2,6,5,0,3]
输出：7
解释：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
     随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。

 >>思路和分析

这道题目是 的进阶版，这里要求至多有k次交易

>>动规五部曲

1.确定dp数组以及下标的含义

一天 一共有 j 个 状态 ，dp[i][j] 中 i 表示 第 i 天，j 为[0 - 2*k] 个状态，dp[i][j]表示第 i 天状态 j所剩最大现金

• 0.没有操作（其实也可以不设置这个状态）
• 1.第一次持有股票
• 2.第一次不持有股票
• 3.第二次持有股票
• 4.第二次不持有股票
• ...

"持有" : 不代表就是当天"买入"！可能昨天就买入了，今天保持有的状态

• ① 我们可以发现，除了0以外，偶数就是不持有，奇数就是持有
• ② 题目要求是至多有k笔交易，那么j的范围就定义为 2*k+1就可以

vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));

2.确定递推公式 

 同理类比剩下的状态，代码如下：

for (int j = 0; j < 2 * k - 1; j += 2) {
    dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
    dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}

推导思路：

-----------------------------------------------------------
第 i 天 的五种状态
dp[i][0] 不操作
 
dp[i][1] 第一天持有股票时剩下的最大金钱
dp[i][1]         dp[i-1][1]
                 dp[i-1][0] - prices[i]
 
dp[i][2] 第一天不持有股票时剩下的最大金钱
dp[i][2]         dp[i-1][2]
                 dp[i-1][1] + prices[i]
 
dp[i][3] 第二天持有股票时剩下的最大金钱
dp[i][3]         dp[i-1][3]
                 dp[i-1][2] - prices[i]
dp[i][4] 第二天不持有股票时剩下的最大金钱
dp[i][4]         dp[i-1][4]
                 dp[i-1][3] + prices[i]
 
-----------------------------------------------------------
dp[i][j+1]       dp[i-1][j+1]
                 dp[i-1][j] - prices[i]
 
dp[i][j+2]       dp[i-1][j+2]
                 dp[i-1][j+1] + prices[i]
 
 
dp[i][j+1] = max(dp[i-1][j+1],dp[i-1][j] - prices[i]);
dp[i][j+2] = max(dp[i-1][j+2],dp[i-1][j+1] + prices[i]);
-----------------------------------------------------------

 3.dp数组初始化

dp[0][0] = 0;
dp[0][1] = -prices[0];
dp[0][2] = 0;
dp[0][3] = -prices[0];
dp[0][4] = 0;
...

同理推出dp[0][j]，当 j 为奇数时都初始化为 -prices[0]。代码如下：

for (int j = 1; j < 2 * k; j += 2) {
    dp[0][j] = -prices[0];
}

4.确定遍历顺序

从递归公式其实已经可以看出，一定是从前向后遍历，因为dp[i]，依靠dp[i - 1]的数值。

5.举例推导dp数组

（1）以输入[1,2,3,4,5],k = 2为例

（2）以输入[3,3,5,0,0,3,1,4],k = 2为例

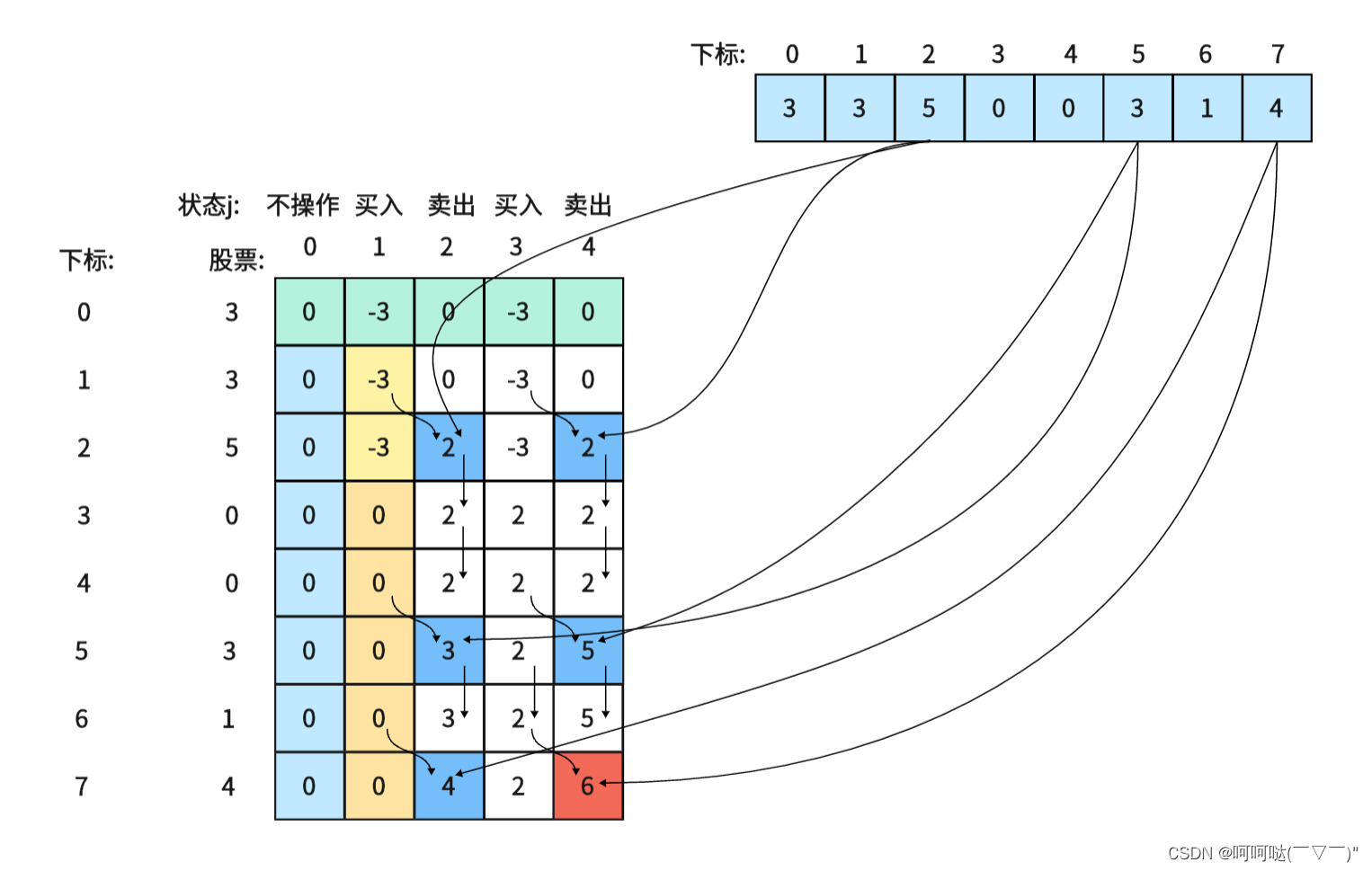
最后一次卖出，一定是利润最大的，dp[prices.size() - 1][2 * k]即红色部分就是最后求解。 

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
 
        if (prices.size() == 0) return 0;
        vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));
        for (int j = 1; j < 2 * k; j += 2) {
            dp[0][j] = -prices[0];
        }
        for (int i = 1;i < prices.size(); i++) {
            for (int j = 0; j < 2 * k - 1; j += 2) {
                dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
                dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
            }
        }
        return dp[prices.size() - 1][2 * k];
    }
};

• 时间复杂度: O(n * k)，其中 n 为 prices 的长度
• 空间复杂度: O(n * k)

>>状态压缩

class Solution {
public:
    // 状态压缩
    int maxProfit(int k, vector<int>& prices) {
        if (prices.size() == 0) return 0;
        int len = prices.size();
        vector<int>dp(2 * k + 1,0);
        for(int j = 1;j < 2 * k;j += 2) {
            dp[j] = -prices[0];
        }
        for(int i=1;i<len;i++) {
            for(int j=0;j < 2*k-1;j += 2) {
                dp[j+1] = max(dp[j+1],dp[j] - prices[i]);
                dp[j+2] = max(dp[j+2],dp[j+1] + prices[i]);
            }
        }
        return dp[2*k];
    }
};

• 时间复杂度: O(n * k)，其中 n 为 prices 的长度
• 空间复杂度: O(k)

参考和推荐文章、视频

动态规划来决定最佳时机，至多可以买卖K次！| LeetCode：188.买卖股票最佳时机4_哔哩哔哩_bilibili

代码随想录 (programmercarl.com) 

来自代码随想录课堂截图：