weixin_40725706

这个屌丝很懒，什么也没留下！

热门标签

机器学习（有监督）——条件随机场CRF_机器学习 crf

作者：weixin_40725706 | 2024-05-19 10:04:52

踩

机器学习 crf

一、定义与原理

二、公式解读

三、代码实现过程

一、定义与原理

条件随机场：给定随机变量X条件下，随机变量Y的马尔可夫随机场。通常是链式的，具有成对马尔可夫性。

马尔可夫性：通俗来说就是当前的序列节点A只和与之相连的节点B、C等有关，与其他的节点D、E等无关。以链式无向序列为例，链式序列拥有马尔可夫性是成对马尔可夫性性：序列Y[y1,y2,....yn]，节点y2与节点y4是相互独立的，而节点y2与节点y1有关系，也与节点y3有关系。

条件随机场的应用：通常进行分类任务时分类器用的是交叉熵损失，而序列标注的任务用的是条件随机场。区别如下图所示：

交叉熵：可以看见前一个类别结果Y1与后一个类别结果Y2是没有关系的，所以每个类别之间是相互独立的

条件随机场：下一个类别Y2受到上一个类别Y1的影响，类别之间是不独立的。以命名实体为例：类别[B，I，O]，B表示名字的第一个字，I表示名字后面的字，O表示不是名字的字。则序列X[他，叫，王，小，明，。]，对应的标签Y[O，O，B，I，I，O]。不可能出现[O，I，B]这样的标签顺序。

二、公式解读

公式：

$P(y|x)=\frac{1}{Z(x)}exp(\sum_{i,k}\lambda _{k}t_{k}(y_{i},y_{i+1},x,i)+\sum_{i,l}\mu _{l}s_{l}(y_{i},x,i))$

$Z(x)=\sum_{y}^{}exp(\sum_{i,k}\lambda _{k}t_{k}(y_{i},y_{i+1},x,i)+\sum_{i,l}\mu _{l}s_{l}(y_{i},x,i))$

$P(y|x)$ 为目标标签序列的概率；

$Z(x)$ 为归一化因子，是所有标签序列得分之和；

$\lambda _{k}$ 为转移权重；

$\mu _{l}$ 为状态权重；

$t_{k}(y_{i},y_{i+1},x,i)$ 和 $s_{l}(y_{i},x,i)$ 为特征函数，通常取0或1；

$i$ 为token，即序列的某个时刻， $k$ 和 $l$ 为特征函数的条件，不同的条件有不同的权重；

$\sum_{i,k}\lambda _{k}t_{k}(y_{i},y_{i+1},x,i)$ 和 $\sum_{i,l}\mu _{l}s_{l}(y_{i},x,i)$ 表示对应条件的特征函数与对应的权重相乘再求和。例如标签为1到3，那么与权重 $\lambda _{1,3}$ 相乘的特征函数 $t_{1,3}(y_{i},y_{i+1},x,i)$ 值为1，其他的 $t_{k}(y_{i},y_{i+1},x,i)$ 值为0。

图解：从图上看其实就是寻找最优路径的过程。

条件随机场举例：标签类别label(1，2，3)，输入序列X(x1，x2，x3)，标签序列Y(1，3，2），转移矩阵T[[t11，t12，t13]，[t21，t22，t23]，[t31，t32，t33]]，状态矩阵实际上就是输入序列的数值[x1，x2，x3]，求目标序列概率P(y|x)

解：

1、计算标签序列1-3的转移得分和状态得分

由标签1转移到标签3，符合该条件的转移权重 $\lambda _{k}$ 为t13，状态权重 $\mu _{l}$ 为x1。对应条件的特征函数肯定是取1，其他情况下为0，所以不考虑其他情况的 $\lambda _{k}$ 和 $\mu _{l}$ 。计算得：t13+x1

2、同理计算标签序列3-2的转移得分和状态得分

汇总得到目标路径1-3-2的得分为：exp(t13+x1+t32+x2)

3、计算归一化因子Z(x)

实际上就是所有路径得分之和：1-1-1、1-1-2、1-1-3、......、3-3-2、3-3-3。

4、计算P(y|x)

目标路径1-3-2的概率P(y|x)=exp(t13+x1+t32+x2)/Z(x)

三、代码实现过程

注意事项：

1、条件随机场模型的公式是希望概率P(y|x)最大，当以P(y|x)为损失值loss时，希望loss最小，因此需要对公式进行修改，将分子分母转为log相减，再取反。这样可以使loss尽量接近与0；

2、转移权重 $\lambda _{k}$ 是模型需要学习的权重矩阵，通过初始化并不停的迭代使目标概率P(y|x)最大；

3、状态权重 $\mu _{l}$ ，也就是输入得分序列X是条件随机场前面接的模型提取到，通常接LSTM、RNN、BERT等特征提取模型；

4、预测时，需要用维特比算法解码得到类别结果；

代码实现：只实现CRF，没有搭建训练模型。训练过程参考：NLP学习笔记——命名实体识别


import torch.nn as nn
import torch
from torch import FloatTensor, Tensor, BoolTensor
from config import Config
 
class CRF(nn.Module):
    def __init__(self, num_labels: int):
        super(CRF, self).__init__()
        self.config = Config()
        self.num_labels = num_labels
        # 使用均匀分布初始化一个转移矩阵
        self.transfer_matrix = nn.Parameter(torch.empty(self.num_labels, self.num_labels))
        nn.init.uniform_(self.transfer_matrix, -0.1, 0.1)
        # 使用均匀分布初始化一个开始矩阵
        self.start_matrix = nn.Parameter(torch.empty(self.num_labels))
        nn.init.uniform_(self.start_matrix, -0.1, 0.1)
        # 使用均匀分布初始化一个结束矩阵
        self.end_matrix = nn.Parameter(torch.empty(self.num_labels))
        nn.init.uniform_(self.end_matrix, -0.1, 0.1)
 
    def forward(self, x: FloatTensor, y: Tensor, mask: BoolTensor
                ) -> Tensor:
        """
        分子除以分母改为相减，希望的概率越大，获取的loss值会负方向趋近于0
        :param x: 特征序列（通常是经过RNN等模型提取到的特征张量）
        :param y: 标签序列
        :param mask: 填充符掩码（特征序列里含有填充符<pad>,对应的标签也有）
        :return: 损失值（负数）
        公式： 概率 = 标签路径上的边和节点得分之和/所有边和节点得分之和
        希望概率最大，因此公式转log使概率从负方向趋近于0。再取反便是loss（正数）
        """
 
        molecule = self.formula_molecule(x, y, mask).to(self.config.device)
        denominator = self.formula_denominator(x, mask).to(self.config.device)
        loss = molecule - denominator
 
        return loss
 
    def formula_molecule(self, x: FloatTensor, y: Tensor, mask: BoolTensor
                         ) -> Tensor:
        """
        计算公式的分子部分
        :param x: 特征序列（通常是经过RNN等模型提取到的特征张量）
        :param y: 标签序列
        :param mask: 填充符掩码（特征序列里含有填充符<pad>,对应的标签也有）
        :return: 分子得分
        """
        batch_size, len_seq, _ = x.size()
        batch_idx = torch.arange(batch_size)  # tensor([ 0,  1,  ....,  batch_size])
        first_y = y[:, 0]  # 每个序列的第一个类别标签
        last_y = y[:, -1]  # 每个序列的最后的类别标签
 
        # 由开始到第一个标签的转移得分
        score = self.start_matrix[first_y]
        # 中间的得分
        for i in range(len_seq-1):
            now_y = y[:, i]  # 当前标签的值y1
            next_y = y[:, i + 1]  # 下一个标签的值y2
            now_mask = mask[:, i]  # 排除掩码部分
            next_mask = mask[:, i + 1]
            transfer = self.transfer_matrix[now_y, next_y]  # 当前时刻y1——>y2的转移权重
            now_x = x[batch_idx, i, now_y]  # 当前标签的值x1
            score += now_x * now_mask + transfer * next_mask
        # 最后的得分
        score += self.end_matrix[last_y]  # 加上最后结束的转移得分
 
        return score
 
    def formula_denominator(self, x: FloatTensor, mask: BoolTensor):
        """
        计算所有边（转移权重）和节点（类别）的总得分作为分母，与有效序列长度有关，越长越大
        :param x: 特征序列（通常是经过RNN等模型提取到的特征张量）
        :param mask: 填充符掩码（特征序列里含有填充符<pad>,对应的标签也有）
        :return: 分别得分
        """
        batch_size, len_seq, _ = x.size()
        # 设置张量形状
        mask = mask.unsqueeze(-1).expand(batch_size, len_seq, self.num_labels)
        start_matrix = self.start_matrix.unsqueeze(0).expand(batch_size, self.num_labels)
        end_matrix = self.end_matrix.unsqueeze(0).expand(batch_size, self.num_labels)
 
        # 第一个token
        x_0 = x[:, 0]
        score = start_matrix + x_0
        # 中间的token
        for i in range(1, len_seq):
            this_x = x[:, i].unsqueeze(1)
            this_mask = mask[:, i]
            this_score = score.unsqueeze(-1) + self.transfer_matrix + this_x   # 当前的结果
            this_score = torch.logsumexp(this_score, dim=1)    # label1-->(label1/label2....)维度求和
            score = torch.where(this_mask, this_score, score)  # 该位置是True就更新为当前结果
        # 最后的token
        score = score + end_matrix
        score = torch.logsumexp(score, dim=1)   # len_seq维度求和
 
        return score
 
    def viterbi_decode(self, x: FloatTensor, mask: BoolTensor):
        """
        预测时，利用维特比算法进行解码，获取到预测的标签序列
        :param x: 特征序列（通常是经过RNN等模型提取到的特征张量）
        :param mask: 填充符掩码（特征序列里含有填充符<pad>,对应的标签也有）
        :return: 标签结果[tensor(标签值), tensor(标签值)]
        """
        batch_size, len_seq, _ = x.size()
        # 用维特比算法筛选最大的得分路径
        # 将维度都拓展成(batch_size, num_labels, num_labels)
        start_matrix = self.start_matrix.unsqueeze(0).expand(batch_size, self.num_labels)
        x_0 = x[:, 0]  # 序列第一个标签
        score = [start_matrix + x_0]  # 记录维特比计算的得分
        path = []   # 记录维特比路径最大的id
        for i in range(1, len_seq):
            # 获取当前时刻的标签
            x_i = x[:, i].unsqueeze(1)
            # 对应路径的得分求和
            this_score = score[i-1].unsqueeze(-1) + self.transfer_matrix + x_i
 
            # 获取上个时刻标签分别到当前时刻标签得分的最大值和标签id(当前同一标签里的路径对比，不同的不比)
            # 例如有标签：1、2。获取上个时刻1与2里到当前时刻1（或2）得分的最大值和id，
            # 所以结果形状为(batch_size,num_labels)
            last_score, last_path = this_score.max(1)
            score.append(last_score)  # 将更新后的得分添加到列表，用于下一个时刻的相加对比
            path.append(last_path)
 
        # 对筛选出来的得分路径进行解码
        effective_length = mask.sum(dim=1).squeeze(0)  # 获取有效序列的长度（去除掩码部分）
        new_path = []
        _, max_index = score[-1].max(1)  # 从最后一个筛选结果里进一步获取最好的结果
        # 将结果添加进去（从后面解码，结果是倒序的）
        new_path.append(max_index.tolist())
        for i in range(len(path)):
            rear_path = path[-1-i]   # 倒数第i个序列的标签集
            batch_id = torch.arange(batch_size)
            max_index = rear_path[batch_id, max_index]  # 根据结果索引max_index查找上一个最好的标签索引
            new_path.append(max_index.tolist())
 
        new_path = torch.tensor(new_path).T
        new_path = torch.flip(new_path, [1]).tolist()  # 因为结果是倒序的，所以将每一行元素再进行倒序
        new_path = [new_path[i][:effective_length[i]] for i in range(batch_size)]  # 只取有效序列部分
 
        return new_path
 
 
if __name__ == '__main__':
    labels = ['a', 'b', 'c']
    X = torch.FloatTensor([[[0.1, 0.2, 0.8], [0.3, 0.8, 0.3], [0.5, 0.6, 0.3]],
                           [[0.3, 0.2, 0.5], [0.3, 0.2, 0.8], [0.9, 0.1, 0.6]],
                           [[0.7, 0.8, 0.8], [0.9, 0.1, 0.8], [0.2, 0.3, 0.6]]])
    Y = torch.LongTensor([[0, 1, 1],
                          [2, 0, 1],
                          [0, 2, 1]])
    Mask = torch.LongTensor([[1, 1, 1],
                             [1, 1, 0],
                             [1, 1, 1]])
 
    crf = CRF(len(labels))
    Loss = crf.forward(X, Y, Mask.byte())
    label = crf.viterbi_decode(X, Mask.byte())
    print(Loss)
    print(label)

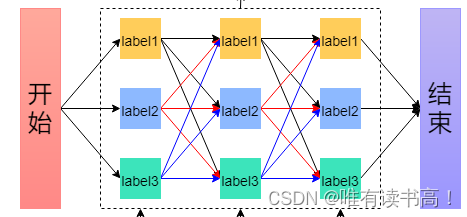
维特比算法：是一种动态规划方法，通俗理解就是在前面时刻找到的最佳路径一定包含在后面时刻找到的最佳路径之中（这个最佳路径不是一个，而是多批路径之中，每一批的最佳路径，最后结合全局从多批里选最佳的一批），具体过程看例子：

如上图所示：

1、根据指向的节点对路径分批：从input1到input2共有九条路径，根据指向input2的标签label1、label2、label3分批，每一批都是黑红蓝共三条。

2、在每一批里选出最佳路径：这样就知道分别指向label1、label2、label3的路径里哪条最好，因为不知道最后选择的标签状态是什么，所以用递推方式分别先选出当前三个标签状态的最优路径。2、从最后3个标签状态选择最佳的标签：根据以上理论推完input3后，只剩下三条指向结束的路径，也就是要从三个标签选最优的标签，定下最优标签后往回查找便能找的最佳路径。

例如：1、input1->input2中：label1的三条路径里最优路径是label2——>label1；

label2的最优路径是label——>label2；

label3的最优路径是label3——>label3；

2、input2->input3中：label1的最优路径是label3——>label1；

label2的最优路径是label3——>label2；

label3的最优路径是label1——>label3；

3、input3->结束中：三个标签里最优的标签是label2，往回找input2->input3的最优标签是label3，同理input1->input2是label3，所以最优标签状态就是label3、label3、label2）。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/weixin_40725706/article/detail/592389