(论文笔记)TABDDPM:使用扩散模型对表格数据进行建模
赞
踩
了解diffusion model:什么是diffusion model? 它为什么好用? - 知乎
摘要
去噪扩散概率模型目前正成为许多重要数据模式生成建模的主要范式。扩散模型在计算机视觉社区中最为流行,最近也在其他领域引起了一些关注,包括语音、NLP 和图形数据。在这项工作中,我们研究了扩散模型的框架是否可用于解决表格问题,其中数据点通常由异构特征的向量表示。表格数据固有的异构性使得准确建模变得非常具有挑战性,因为各个特征可能具有完全不同的性质,即其中一些特征可能是连续的,而另一些特征可能是离散的。为了解决此类数据类型,我们引入了 TabDDPM——一种可以普遍应用于任何表格数据集并处理任何类型特征的扩散模型。我们在一系列基准上对 TabDDPM 进行了广泛的评估,并证明了它优于现有 GAN/VAE 替代方案,这与扩散模型在其他领域的优势一致。此外,我们表明 TabDDPM 适用于隐私导向的设置,其中原始数据点不能公开共享。 TabDDPM 的源代码和我们的实验可在 https://github.com/rotot0/tab-ddpm 上找到。
1.引言
去噪扩散概率模型 (DDPM) (Sohl-Dickstein 等人,2015 年;Ho 等人,2020 年) 最近成为生成模型界研究的热门话题,因为它们在单个样本的真实感和多样性方面往往优于其他方法 (Dhariwal & Nichol,2021 年)。 DDPM 最令人印象深刻的成功是在自然图像领域 (Dhariwal & Nichol, 2021; Saharia et al, 2022; Rombach et al, 2022) 证明的,其中扩散模型的优势在诸如着色 (Song et al, 2021)、修复 (Song et al, 2021)、分割 Baranchuk et al (2021)、超分辨率 (Saharia et al, 2021; Li et al, 2021)、语义编辑 (Meng et al, 2021) 等应用中得到成功利用。除了计算机视觉之外,DDPM 框架还在其他领域得到了研究,例如 NLP(Austin 等,2021;Li 等,2022)、波形信号处理(Kong 等,2020;Chen 等,2020)、分子图(Jing 等,2022;Hoogeboom 等,2022)、时间序列(Tashiro 等,2021),证明了扩散模型在广泛问题中的普适性。
本文的工作目的是了解 DDPM 是否可以扩展到表格问题。由于各个特征的异质性(有的特征是连续数据有的是离散数据)以及典型表格数据集的规模相对较小,训练高质量的表格数据模型与计算机视觉或 NLP 相比更具挑战性。在本文中,作者表明,尽管存在这两个复杂性,但扩散模型可以成功地近似表格数据的典型分布,从而在大多数基准测试中实现最优的性能。
更详细地说,我们工作的主要贡献如下:
- 引入了 TabDDPM — 针对表格问题的最简单 DDPM 设计,可应用于任何表格任务,并可处理混合数据,包括数值和分类特征。
- 证明 TabDDPM 优于为表格数据设计的替代方法,包括文献中基于 GAN 和基于 VAE 的模型,并说明了多个数据集的这一优势来源。
- 当使用合成数据替代无法共享的真实用户数据时,TabDDPM 生成的数据似乎是隐私问题场景的“最佳点”。
2.相关工作
扩散模型 (Sohl-Dickstein 等人,2015 年;Ho 等人,2020 年) 是一种生成建模范式,旨在通过马尔可夫链的端点近似目标分布,该链从给定的参数分布(通常是标准高斯分布)开始。每个马尔可夫步骤都由深度神经网络执行,该网络可以有效地学习使用已知高斯核来反转扩散过程。 Ho 等人证明了扩散模型和分数匹配的等价性 (Song & Ermon,2019 年;2020 年),表明它们是通过迭代去噪过程将简单的已知分布逐步转换为目标分布的两个不同视角。最近的几项工作 (Nichol,2021 年;Dhariwal & Nichol,2021 年) 开发了更强大的模型架构以及不同的高级学习协议,这导致 DDPM 在计算机视觉领域的生成质量和多样性方面“胜过”GAN。在我们的工作中,我们证明了扩散模型也可以成功地用于表格问题。
表格问题的生成模型目前是机器学习社区的一个活跃的研究方向(Xu 等人,2019 年;Engelmann & Lessmann,2021 年;Jordon 等人,2018 年;Fan 等人,2020 年;Torfi 等人,2022 年;Zhao 等人,2021 年;Kim 等人,2021 年;Zhang 等人,2021 年;Nock & GuillameBert,2022 年;Wen 等人,2022 年),因为许多表格任务对高质量的合成数据有着很大的需求。首先,表格数据集的大小通常有限,这与视觉或 NLP 问题不同,因为互联网上有大量“额外”数据可用。其次,适当的合成数据集不包含实际的用户数据,因此它们不受 GDPR 类法规的约束,并且可以公开共享而不会违反匿名性。最近的研究开发了大量模型,包括表格 VAE(Xu et al,2019)和基于 GAN 的方法(Xu et al,2019;Engelmann & Lessmann,2021;Jordon et al,2018;Fan et al,2020;Torfi et al,2022;Zhao et al,2021;Kim et al,2021;Zhang et al,2021;Nock & Guillame-Bert,2022;Wen et al,2022)。通过对大量公共基准进行广泛的评估,我们表明我们的 TabDDPM 模型超越了现有的替代方案,而且往往领先幅度很大。
“浅层”合成生成。与非结构化图像或自然文本不同,表格数据通常是结构化的,即各个特征通常是可解释的,并且尚不清楚它们的建模是否需要多层“深层”架构。因此,简单的插值技术,如 SMOTE(Chawla 等人,2002 年)(最初提出用于解决类别不平衡问题)可以作为简单而强大的解决方案,如(Camino 等人,2020 年)中所示,其中 SMOTE 在小类过采样方面的表现优于表格 GAN。在实验中,我们从隐私保护的角度展示了 TabDDPM 生成的合成图像相对于插值技术生成的合成图像的优势。
3.背景
扩散模型(Sohl-Dickstein 等人,2015 年;Ho 等人,2020 年)是基于似然的生成模型,通过正向和反向马尔可夫过程处理数据。正向过程 逐渐将噪声添加到来自数据分布
的初始样本
,从预定义分布
中采样噪声,方差为
。逆扩散过程
逐渐对潜在变量
进行去噪,并允许从
生成新的数据样本。分布
通常未知,并由具有参数 θ 的神经网络近似。这些参数是通过优化变分下限从数据中学习的:公式(1)
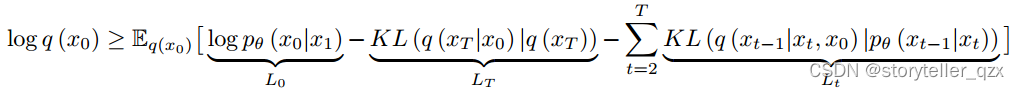
高斯扩散模型在连续空间 中运行,其中正向和反向过程以高斯分布为特征:
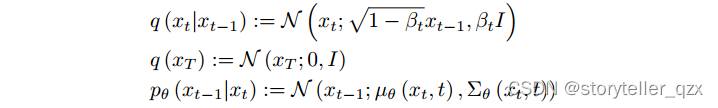
Ho 等人 (2020) 建议使用具有常数 的对角线
,并计算
作为
和
的函数:
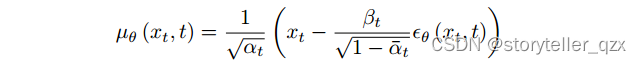
其中 且
预测噪声数据样本
的“真实”噪声分量。实际上,目标 (1) 可以简化为
和
在所有时间步 t 上的均方误差之和: 公式(2)
![]()
多项式扩散模型 (Hoogeboom 等人,2021) 旨在生成分类数据,其中 是具有 K 个值的独热编码分类变量。多项式正向扩散过程将
定义为分类分布,该分布通过 K 个类的均匀噪声破坏数据:
![]()
从上面的方程中,可以推导出后验概率 :
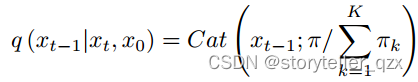
其中,。
逆分布 被参数化为
,其中
由神经网络预测。然后,训练模型以最大化变分下界 (1)。
4.TABDDPM
在本节中,我们描述了 TabDDPM 的设计及其影响模型有效性的主要超参数。
TabDDPM 使用多项式扩散来对分类特征和二元特征进行建模,使用高斯扩散来对数值特征进行建模。更详细地讲,对于一个表格数据样本 ,其中包含
个数值特征
和 C 个分类特征
(每个特征有
个类别),我们的模型将分类特征的独热编码版本作为输入(即
),并使用标准化的数值特征。因此,输入
的维数为 (
)。对于预处理,我们使用 scikit-learn 库(Pedregosa 等人,2011)中的高斯分位数变换。每个分类特征都由单独的前向扩散过程处理,即所有特征的噪声成分都是独立采样的。 TabDDPM 中的反向扩散步骤由多层神经网络建模,该网络具有与
相同的维数输出,其中前
个数值是高斯扩散的
预测,其余数值是多项式扩散的
i 预测。
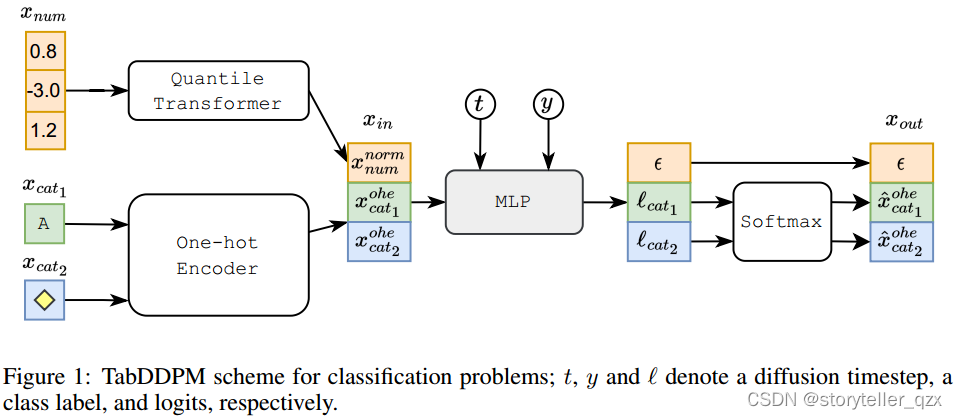
TabDDPM 模型用于分类问题的示意图如图1所示。该模型通过最小化高斯扩散项的均方误差 (公式 (2))和每个多项式扩散项的 KL 散度
(公式 (1))之和来进行训练。多项式扩散的总损失还会额外除以分类特征的数量。公式(3)
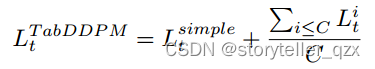
对于分类数据集,我们使用一个类条件模型,即学习 。对于回归数据集,我们将目标值视为一个额外的数值特征,并学习联合分布。
为了建模逆过程,我们使用一个简单的 MLP 架构,改编自 (Gorishniy 等人,2021):公式(4)

与 (Nichol, 2021; Dhariwal & Nichol, 2021) 一样,表格输入 、时间步长 t 和类标签 y 的处理如下。公式(5)
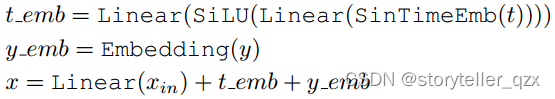
其中 SinTimeEmb 指的是正弦时间嵌入,如 (Nichol, 2021; Dhariwal & Nichol, 2021) 中所示,维度为 128。公式 5 中的所有线性层都具有固定的投影维度 128。
TabDDPM 中的超参数至关重要,因为在实验中我们观察到它们对模型有效性有很大影响。表 1 列出了我们建议使用的主要超参数以及每个超参数的搜索空间。实验部分详细描述了调整过程。
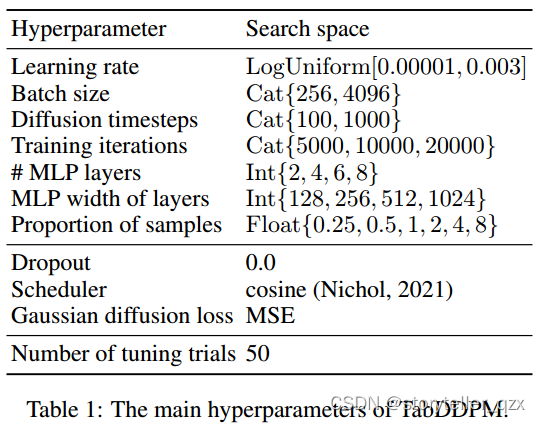
简述上面的过程:
(1) 数据预处理
- 数值特征:对数值特征进行高斯分位数变换,使其接近标准正态分布。
- 离散特征:将离散特征转换为独热编码形式(one-hot encoding)。
- (2)正向扩散(Forward Diffusion)
- 数值特征:通过高斯扩散过程处理,即向数值特征添加高斯噪声,逐步扰动数据,使其接近高斯分布。
- 离散特征:每个离散特征独立处理,通过多项扩散过程添加噪声。每个类别特征的噪声分量是独立采样的。
(3) 构建输入数据:将处理的数值特征和one-hot编码的离散特征合并成输入向量,其维度为
。
(4)模型构建和训练:使用一个多层感知器(MLP)来建模反向扩散过程。该MLP的输出维度与 相同。
- 数值特征预测:MLP输出向量的前
个坐标用于预测高斯扩散过程中的噪声,从而恢复数值特征。
- 离散特征预测:MLP输出向量的剩余坐标用于预测多项扩散过程中的噪声,从而恢复离散特征。
(5)损失函数
- 数值特征:通过最小化均方误差(mean-squared error,
)来训练模型。
- 类别特征:通过最小化每个多项扩散过程的KL散度(
)来训练模型。所有类别特征的总损失除以类别特征的数量
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/weixin_40725706/article/detail/597137
Copyright © 2003-2013 www.wpsshop.cn 版权所有,并保留所有权利。


