TDOA定位 chan算法和Taylor算法比较仿真 matlab_tdoa和泰勒是一个吗

最近在学习TDOA定位算法，需要比较chan（查恩算法）和Taylor（泰勒级数算法）的定位效果。
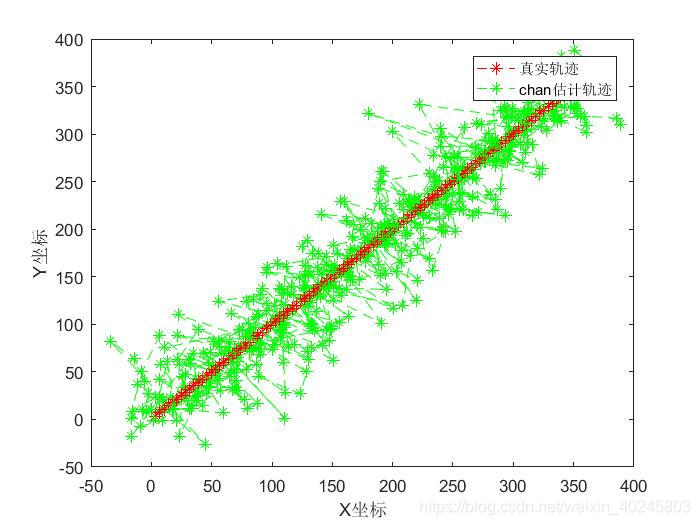
分别实现的效果图：


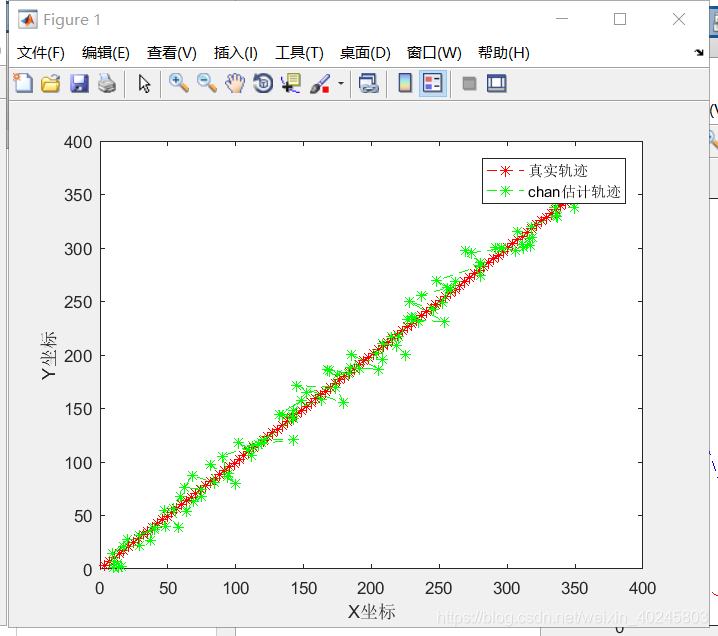
运动目标从零点开始沿x=y做匀速运动。
观测站坐标如下：

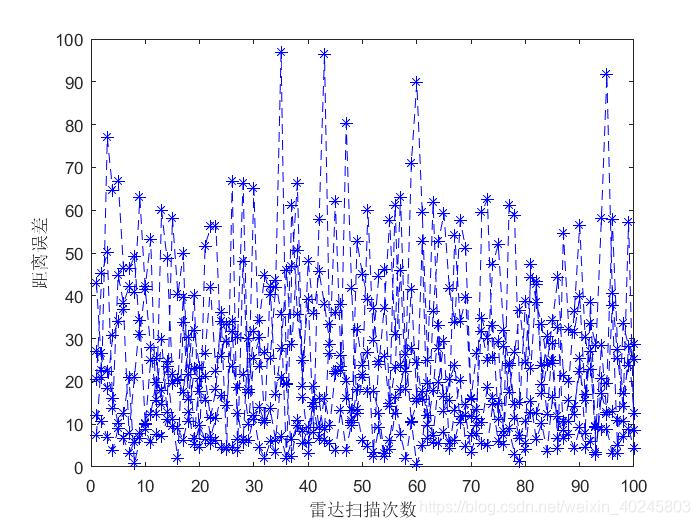
在不同的雷达测距误差下的定位误差为：

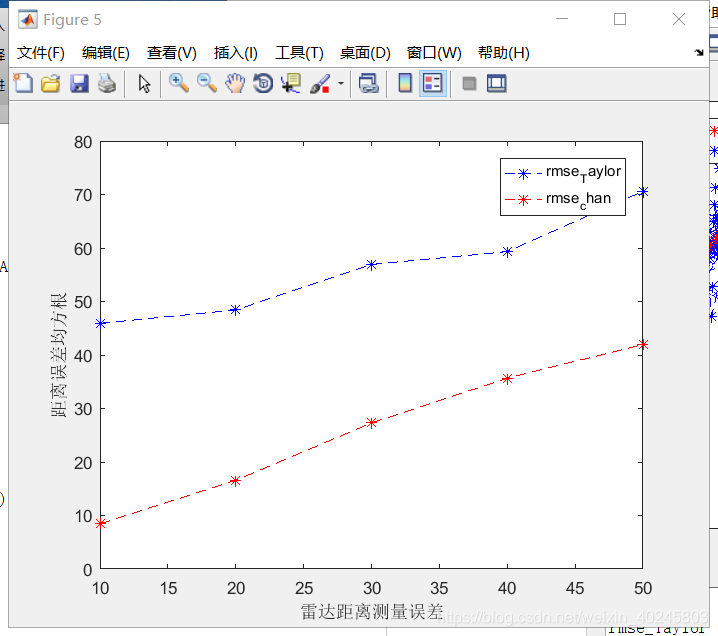
其实仿真代码还有不足，Taylor算法初值的确定非常重要，仿真中直接把真实值作为了初值，实际上需要改为第一次LS定位点或WLS定位点，比较符合真实情况。
不过，到此已经能比较明显的比较出两种算法的不同之处了。
需要源码的同学可以到我的主页下载

感谢 Iam_Flash的提问，上传程序中chan算法的pos应在第二次WLS定位中选择，由于参考基站的位置会影响第二次WLS的求解结果，所以建议把参考基站设置为（0，0），保证待测目标出现在以参考基站为原点的第一象限上，保证第二次求解WLS不会出现虚数。当然也可以对WLS出现虚数的值进行处理还原出估计值。
未修改参考基站的坐标，直接改chan的pos，会出现如下情况：

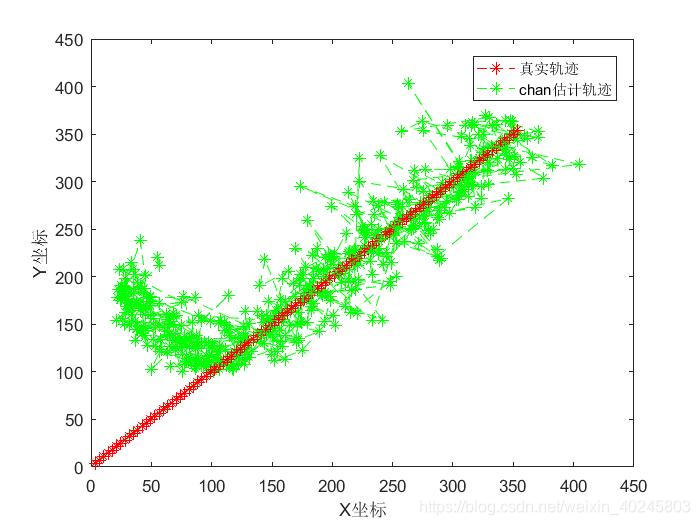
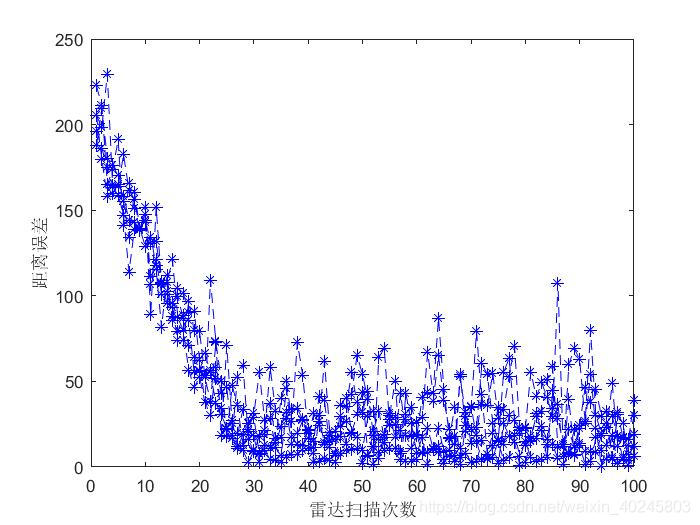
求解出虚数的结果被滤除。
修改参考坐标后，将参考基站坐标改为（-100，-100）

function [rmse_c,rmse_T] = TDOAchan_Taylor_comparise(noise)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%     设置基站信息
%  delta  TDOA测量误差的标准差,用于产生Q矩阵
%  M      参考基站外的基站数量
%  Xb = -100;Yb = -100;    %参考的基站坐标
%   c     光速
%   X     参考基站的坐标
%   T: 雷达的扫描间隔，此时设为1秒
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
delta = noise;  
M=4;
Xb = -100;Yb =-100;%参考的基站坐标
c=3e8;
X = zeros(M,2);
T = 1;
%生成其他基站的坐标 
a = 2*pi/M;
for i=1:M
     X(i,1) = 3000*cos(a*(i-1));
     X(i,2) = 3000*sin(a*(i-1));
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

重新输出结果：