ECC、ECDH或是ECDSA。第一个术语是椭圆曲线密码学（Elliptic Curve Cryptography） 的缩写，后两个是基于它的算法名称。
如今，我们可以在TLS、PGP和SSH中见到椭圆曲线加密系统，这是现代网络和IT世界所依赖的三种主要技术。比特币和其他加密货币就更不用说了。
在ECC流行起来之前，几乎所有的公钥算法都是基于RSA、DSA和DH ———— 基于模运算的可选加密系统。RSA及其友类算法在当前仍非常重要，经常与ECC一并使用。不过，RSA及其友类算法背后的原理很容易解释，因而被广泛理解，一些简单的实现也可以很容易编写出来；但ECC的实现基础对于大多数人来说仍很神秘。
通过一系列的博文，我打算用一个通俗的方式介绍椭圆曲线密码学。我的目标不是提供ECC完整和详细的指导（网上有这方面的充足信息），而是简单概述“ECC是什么、为什么它被认为是安全的”，避免把时间浪费在长篇的数学证明和恼人的实现细节上。我还将提供一些辅助示例以及可视化图形工具和脚本给大家使用。
具体来说，我将触及以下主题：
1. 基于实数域的椭圆曲线和群公理（本文中涉及）
2. 基于有限域的椭圆曲线和离散对数问题
3. 密钥对的生成以及两个ECC算法：ECDH和ECDSA
4. 破坏ECC安全性的算法，并与RSA作对比
为了能够理解本文所述的内容，你需要了解集（set)理论、几何、模运算等基本概念，并大致知道对称式和非对称式加密。此外，你需要清楚的知道什么是“易解”问题，什么是“难解”问题，以及它们在密码学中的角色。
准备好了吗？开始！
椭圆曲线
首先，什么是椭圆曲线？ MathWorld 线上数学百科全书给出了一个极好并完整的定义。不过，针对我们的学习目的，椭圆曲线将简化为用下面这个等式所描述的点的集合：
其中， 4a3 + 27b2 ≠ 0 (这是为了排除奇曲线)。上面的等式称为椭圆曲线的魏尔斯特拉斯范式（ Weierstrass normal form）
不同的椭圆曲线的不同形状 (b = 1, a 取值由 2 变化至 -3).
奇点类型: 左侧, 带一个尖角的曲线 (y2 = x3)。右侧, 带一个自交叉的曲线 (y2 = x3 – 3x + 2). 这两种都不是有效的椭圆曲线。
根据a和b的值，椭圆曲线在平面上可以呈现不同形状。可以很容易看出并验证： 椭圆曲线是关于x-轴对称的。为了实现我们的目标，我们还需要把一个无穷远点（亦称之为理想点) 视为椭圆曲线的一部分。从现在开始，我们将用符号0（零）来代表无穷远点。
如果我们想显式地将无穷远点纳入考虑，我们可以按如下的方式细化椭圆曲线的定义：
群
数学中的“群”是一个由我们定义了一种二元运算的集合，二元运算我们称之为“加法”，并用符号“+”来表示。为了让一个集合G成为群，必须定义加法运算并使之具有以下四个特性：
1. 封闭性：如果a和b是集合G中的元素，那么（a + b)也是集合G中的元素。
2. 结合律：(a + b) + c = a + (b + c);
3. 存在单位元0，使得a + 0 = 0 + a =a;
4. 每个元素都有逆元，即：对于任意a，存在b，使得a + b = 0.
如果我们增加第5个条件：
5. 交换律： a + b = b + a
那么，称这个群为阿贝尔（abelian)群。
配上通常概念的加法时，整数的集合Z就是一个群（同时还是个阿贝尔群）。而自然数的集合（N）就不是群，因为它不满足第4个特性。
“群”很有用，因为一旦我们证明它具备上述4个特性，那么我们就可以自由地获取到一些其他特性。比如：单位元是唯一的；此外，逆元也是唯一的，即：对于每一个a，存在唯一的一个b，使得a + b = 0 （我们可以将b写成-a）。后面我们会发现，群的这些特性以及其他存在的事实，或者直接或者间接，对于我们来说非常重要。
椭圆曲线的群公理
我们可以定义一个基于椭圆曲线的群。如下：
• 群中的元素是一条椭圆曲线上的点;
• 单位元为无穷远点O;
• 点P的逆元是其关于x-轴的对称点;
• 加法，满足以下规则: 对于3个处在同一直线上的非零点 P, Q 和 R, 它们的和 P + Q + R = 0.
同一直线上的三个点之和等于0.
注意一下最后一个规则，我们需要的只是三个点同线，与点的次序无关。这意味着，如果P、Q和R同线，那么P + (Q + R) = Q + (P + R) = R + (P + Q) = • • • = 0. 这样，我们直观地证明了我们的“+”运算既满足结合律也满足交换律：我们创建了一个阿贝尔群。
到目前还很不错。但我们如何实际计算任意两点之和呢？
几何加法
得益于我们使用的是一个阿贝尔群，我们可以把 P + Q + R = 0 写成P + Q = –R。方程的这一形式，让我们可以推导出计算两点P和Q之和的几何方法：画一条过P和Q点的直线，这条直线与曲线相交得到第3个点R（这一事实意味着P、Q、R必然共线）。如果我们获取了该点的逆元-R，那么我们就得到了P + Q的结果。
过P和Q画一条直线。该直线与曲线相交与第3点R。与之对称的点-R即为P+Q 的结果
这种几何方法可以成立，但还需一些改进。特别是，我们需要回答以下几个问题：
• 当P = 0或Q = 0时怎么办? 显然，我们无法画任何直线（0点不在xy-平面上）。不过，由于我们定义了0点为单位元，所以，对于任意P和任意Q，都有：P + 0 = P ， 0 + Q = Q
• 当P= –Q时怎么办? 这种情况下，通过两点的直线是一条垂线，与曲线不会有第三个交点。不过，由于P是Q的逆元，那么由逆元的定义可知P + Q = P + (-P) = 0 .
• 当P= Q时怎么办? 这种情况下，经过该点的直线有无数条。事情开始有点复杂了。不过，先想像一个点 Q’ ≠ P。如果我们令Q’ 向P逼近，越来越靠近P会怎么样？
随着两个点越来越接近，过这两点的直线最终变成了曲线的切线
随着Q’ 趋向P, 过P和Q’ 的直线最终成为曲线的切线。看到这一点，我们可以定义 P + P = –R, 其中R是过P点的切线与曲线的交点。
• 当P ≠ Q，但找不到第三个点R时怎么办? 这种情况和上面那个非常类似。实际上，这是因为过P和Q的直线与曲线相切。
如果直线与曲线只有两个交点，那么该直线为曲线的切线。可以很容易地看出，两点相加的结果是其中一点的对称点
• 假设P是切点，在上一情况中，我们已经得出P + P = –Q. 等式现在变为 P + Q = –P。 如果Q 是切点，正确的等式应为 P + Q = –Q.
现在，用几何方法可以完全覆盖所有情况了。用一支铅笔和一把尺，我们可以做任意椭圆曲线上所有点的加法运算。如果你想试试，请到 HTML5/JavaScript visual tool 看一下，这是我建的一个工具，用来计算椭圆曲线的加法!
代数加法
如果我们想把点的加法运算计算机来完成，那么需要将几何方法转化为代数方法。将上面描述的规则转换为一组公式看似简单，实际上是非常繁琐的，因为需要求解三次方程。因此，这里我只通报结果。
首先，先抛开最恼人的极端情况。我们已经知道P + (-P) = 0, 还知道P + 0 = 0 + P = P。所以，在我们的公式中 ，我们将避免这两种情况，只考虑两个非零、非对称点 P = (xP, yP) 和Q = (xQ, yQ).
如果 P 和 Q 不相同， (xP ≠ xQ), 过这两点的直线斜率为:
该直线与椭圆曲线交于第三点 R = (xR, yR):
或是, 等价形式:
因此，(xP, yP) + (xQ, yQ) = (xR, –yR) (注意正负号，记住P + Q = –R).
如果我们想检查这一结果是否正确，我们将不得不检查R是否在曲线上，同时P、Q、Q是共线。检查点是否共线轻而易举，但检查R是否在曲线上就不容易了，因为需要求解三次方程，这可不是什么好玩的事儿。
不过，我们可以用一个例子来试一下：根据 可视化工具的计算， 当 P = (1, 2) 、Q = (3, 4) ，椭圆曲线 y2 = x3 – 7x + 10, 两点之和 P + Q = –R = (-3, 2). 让我们看一下与我们的公式是否一致:
好的，正确!
注意上面的公式即使在其中一个点P或Q是切点的情况下也成立。让我们试一下P = (-1, 4) 、 Q = (1, 2).
我们计算出 P + Q = (1, -2), 与使用 可视化工具计算出的结果相同。
P = Q 的情况需要做点不同的处理：方程中 xR 和 yR 相同, 由于 xP = xQ, 我们必须使用不同的公式来计算斜率：
注意，我们可以料到，m的表达式实际是下面这个函数的一阶导数:
为了证明结果的有效性，只要检查R是否在曲线上，以及P和R在曲线上只有两个交点就足够了。但同样，我们不去证明这一事实，而是试算一个例子: P = Q = (1, 2).
公式计算出 P + P = –R = (-1, -4).正确!
尽管推导过程真的是极其繁琐，不过最后的公式还是很简洁。这要感谢魏尔斯特拉斯范式：要是没有这一范式，最后的公式会真的又长又复杂。
标量乘法
在加法之外，我们还可以定义另一种运算：标量乘法，即：
nP，其中n为自然数。我为标量乘法也写了个 可视化工具 ，如果你想试算时可以使用。
用这种形式表示时，计算nP似乎需要n次加法运算。如果n有k个二进制位，那么算法的时间复杂度将为O（2^k)，这真不是很好。不过存在一些更快的算法。
其中一种是“加倍（double)与相加（add)”算法。
计算的原理可以用一个例子来更好地解释。取n = 151。它的二进制表示形式为100101112 。这一二进制表示形式可以转换为一系列2的幂之和。
(取n的 每个二进制位上的数字，并用它乘以一个2的幂.)
用这种方法，我们可以将n这样写:
“加倍（double)与相加（add)”算法需要这样做:
• 取 P.
• 加倍，得到2P.
• 2P与P相加(为了得到 21P + 20P).
• 加倍 2P，得到22 P.
• 与前一结果相加 (得到 22P + 21P + 20P).
• 加倍 22P，得到23P.
• 对23P不做任何操作.
• 加倍23P，得到24P.
• 与前一结果相加 (得到 24P + 22P + 21P + 20P).
• …
最后，我们可以计算151 • P ，只需7次“加倍”运算和4次“相加”运算。
如果还不够清楚，这里有一个实现该算法的python代码段：
如果“加倍”和“相加”操作复杂度均为O(1),那么 该算法的时间复杂度为O(log n) (或是O(k)，如果我们考虑的是二进制位的长度），这相当不错。比最初O(n)的算法肯定要好得多。
对数
给定n和P, 我们现在至少有一个多项式时间算法来计算Q = nP。不过，逆运算需要计算多少轮呢？如果已知Q和P，我们想求解n会怎么样？这一问题被称为对数问题。我们称之为“对数”而不是“除法”是为了与其他加密系统（在术语上）保持统一（那些系统中，不称“乘法”，而称“幂”）。
我不知道任何关于对数问题的“易解”算法，不过，通过摆弄乘法 ，很容易发现一些模式。例如，对于曲线 y2 = x3 – 3x + 1和点 P = (0, 1). 我们可以立即验证出, 如果n为奇数，nP在曲线的左半面，如果n为偶数，nP在曲线的右半面。如果我们尝试更多次，我们或许可以找出更多的模式，最终可以让我们写出一个算法来高效计算那条曲线的对数问题。
不过，对数问题有一个变体：离散对数问题。在下一篇博文中，我们将看到，当我们对椭圆曲线的域进行缩减后，标量乘法仍旧”易解“，而离散对数问题成为了”难解”问题。这种双重性是椭圆曲线密码学的关键基石。
PS: 补充一下 公式 Xr = m ^2 – Xp – Qq 是怎么推导出的：
关于三次方程的求解过程，此处不再赘述。有兴趣的可以看一下这个视频：https://www.youtube.com/watch?v=7leAwQHVvz0
求解后，得到三个根：
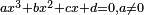
![{}_{x_1=-\frac{b}{3 a}+ \sqrt[3]{\frac{bc}{6a^2}-\frac{b^3}{27a^3}-\frac{d}{2a}+\sqrt{{\color{red}\left(\frac{bc}{6a^2}-\frac{b^3}{27a^3}-\frac{d}{2a}\right)^2+ \left(\frac{c}{3a}-\frac{b^2}{9a^2}\right)^3}}}+\sqrt[3]{\frac{bc}{6a^2}-\frac{b^3}{27a^3}-\frac{d}{2a}-\sqrt{\left(\frac{bc}{6a^2}-\frac{b^3}{27a^3}-\frac{d}{2a}\right)^2+ \left(\frac{c}{3a}-\frac{b^2}{9a^2}\right)^3}}}](https://upload.wikimedia.org/math/3/7/8/3783731b1f4e345ebb96c4dd6b2f2e7b.png)
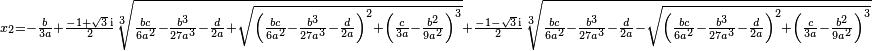
单独求任何一个根都很麻烦，不过，如果把三个根相加会发现：x1 + x2 + x3 刚好等于 -b，也就是只与其中二次方项的系数b有关。
由于我们已经知道曲线上的两个点Xp和Xq了，那么求Xr就有了简单方法：
由直线方程可知：(y – y1) = m (x – x1)， y = m(x – x1) + y1。 ……(1)
将（1）代入到椭圆方程 y2 = x3 + ax + b ……(2)
得到： [m(x - x1) + y1] 2 = x3 + ax + b …….(3)
通过判别式判断出这个三次方程有三个解，所以（3）也可以改写成下面的形式
（x – x1) (x – x2)(x – x3) = 0 ……..(4)
根据前面的推导，可知这个三次方程的三个根之和等于左边这个二次方项的系数。
由（3）式可知，其中二次方项的系数为m2，所以 x1 + x2 + x3 = m2.
解得第三个点 x3 =m2 – x1 – x2
即： Xr = m2 – Xp – Qq
